Lernlatenz: Warteschlangentheorie

Das Thema Latenz im Laufe der Zeit wird nicht nur in Yandex in verschiedenen Systemen interessant. Dies geschieht, wenn in diesen Systemen Servicegarantien angezeigt werden. Tatsache ist natürlich, dass es wichtig ist, den Benutzern nicht nur eine Gelegenheit zu versprechen, sondern auch den Empfang mit einer angemessenen Antwortzeit zu garantieren. Die „Angemessenheit“ der Reaktionszeit ist natürlich für verschiedene Systeme sehr unterschiedlich, aber die Grundprinzipien, nach denen sich die Latenz in allen Systemen manifestiert, sind gemeinsam und können isoliert von den Besonderheiten betrachtet werden.

Mein Name ist Sergey Trifonov, ich arbeite im Team von Real-Time Map Reduce in Yandex. Wir entwickeln eine Plattform für die Echtzeit-Datenflussverarbeitung mit Antwortzeiten von Sekunden und Sekunden. Die Plattform steht internen Benutzern zur Verfügung und ermöglicht ihnen, Anwendungscode für ständig eingehende Datenströme auszuführen. Ich werde versuchen, einen kurzen Überblick über die Grundkonzepte der Menschheit zum Thema Latenzanalyse in den letzten hundertzehn Jahren zu geben, und jetzt werden wir versuchen zu verstehen, was genau mit der Warteschlangentheorie über Latenz gelernt werden kann.

Das Phänomen der Latenz wurde meines Wissens im Zusammenhang mit dem Aufkommen von Warteschlangensystemen - Telefonkommunikationsnetzen - systematisch untersucht. Die Warteschlangentheorie begann mit der Arbeit von A. K. Erlang im Jahr 1909, in der er zeigte, dass die Poisson-Verteilung auf zufälligen Telefonverkehr anwendbar ist. Erlang entwickelte eine Theorie, die seit Jahrzehnten zum Entwurf von Telefonnetzen verwendet wird. Die Theorie erlaubt es uns, die Wahrscheinlichkeit einer Dienstverweigerung zu bestimmen. Bei Telefonnetzen mit leitungsvermittelten Kanälen ist ein Fehler aufgetreten, wenn alle Kanäle besetzt sind und der Anruf nicht getätigt werden kann. Die Wahrscheinlichkeit dieses Ereignisses musste kontrolliert werden. Ich wollte eine Garantie haben, dass zum Beispiel 95% aller Anrufe bedient werden. Mit den Erlang-Formeln kann ermittelt werden, wie viele Server zur Erfüllung dieser Garantie benötigt werden, wenn die Dauer und Anzahl der Anrufe bekannt sind. Tatsächlich geht es bei dieser Aufgabe nur um Qualitätsgarantien, und heute lösen die Menschen immer noch ähnliche Probleme. Systeme sind jedoch viel komplexer geworden. Das Hauptproblem der Warteschlangentheorie besteht darin, dass sie in den meisten Institutionen nicht gelehrt wird und nur wenige Menschen die Frage außerhalb der üblichen M / M / 1-Warteschlange verstehen (siehe Notation unten ). Es ist jedoch bekannt, dass das Leben viel komplizierter ist als dieses System. Daher schlage ich vor, unter Umgehung von M / M / 1 sofort zum interessantesten zu gehen.

Durchschnittswerte

Wenn Sie nicht versuchen, vollständige Kenntnisse über die Wahrscheinlichkeitsverteilung im System zu erlangen, sondern sich auf einfachere Fragen konzentrieren, können Sie interessante und nützliche Ergebnisse erzielen. Der berühmteste von ihnen ist natürlich der Satz von Little . Es ist auf ein System mit einem beliebigen Eingabestream, einem internen Gerät beliebiger Komplexität und einem beliebigen Scheduler anwendbar. Die einzige Voraussetzung ist, dass das System stabil ist: Durchschnittliche Antwortzeiten und Warteschlangenlängen müssen vorhanden sein, dann werden sie durch einen einfachen Ausdruck verbunden

$$

$$L = \ lambda W$$

wo $$$L$ - die durchschnittliche zeitliche Anzahl von Anforderungen im betrachteten Teil des Systems [Stk.], $$$W$ - die durchschnittliche Zeit, für die Anforderungen diesen Teil des Systems durchlaufen, $$$\ lambda$ - die Geschwindigkeit des Eingangs von Anfragen an das System [pcs / s]. Die Stärke des Satzes besteht darin, dass er auf jeden Teil des Systems angewendet werden kann: Warteschlange, Executor, Warteschlange + Executor oder das gesamte Netzwerk. Oft wird dieser Satz ungefähr so ​​verwendet: "1 Gbit / s-Strom strömt auf uns zu, und wir haben die durchschnittliche Antwortzeit gemessen, und es sind 10 ms, daher haben wir durchschnittlich 1,25 MB im Flug." Diese Berechnung ist also nicht wahr. Genauer gesagt ist dies nur dann der Fall, wenn alle Anforderungen dieselbe Größe in Byte haben. Der Satz von Little zählt Abfragen in Stücken, nicht in Bytes.

Wie man den Satz von Little benutzt

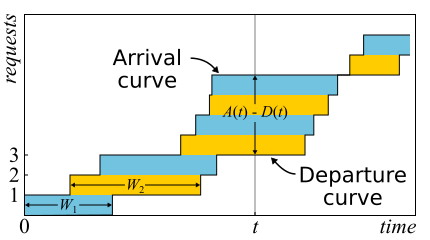
In der Mathematik ist es oft notwendig, Beweise zu studieren, um einen echten Einblick zu erhalten. Dies ist nur der Fall. Der Satz von Little ist so gut, dass ich hier eine Skizze des Beweises gebe. Eingehender Verkehr wird durch die Funktion beschrieben $$$A (t)$ - Die Anzahl der Anfragen, die zu diesem Zeitpunkt angemeldet sind $$$t$ . Ähnlich $$$D (t)$ - Die Anzahl der Anfragen, die zu diesem Zeitpunkt abgemeldet sind $$$t$ . Der Zeitpunkt des Eintritts (Austritts) der Anforderung gilt als der Zeitpunkt des Eingangs (der Übertragung) ihres letzten Bytes. Die Grenzen des Systems werden nur durch diese Zeitpunkte bestimmt, daher ist der Satz weithin anwendbar. Wenn Sie Diagramme dieser Funktionen in denselben Achsen zeichnen, ist dies leicht zu erkennen $$$A (t) - D (t)$ Ist die Anzahl der Anforderungen im System zum Zeitpunkt t und $$$W_n$ - Antwortzeit der n-ten Anfrage.

Der Satz wurde erst 1961 formell bewiesen , obwohl die Beziehung selbst schon lange vorher bekannt war.

Wenn Anforderungen innerhalb des Systems neu angeordnet werden können, ist alles etwas komplizierter. Der Einfachheit halber gehen wir davon aus, dass dies nicht der Fall ist. Obwohl der Satz auch in diesem Fall wahr ist. Berechnen wir nun die Fläche zwischen den Diagrammen. Es gibt zwei Möglichkeiten, dies zu tun. Erstens nach den Spalten - wie die Integrale normalerweise denken. In diesem Fall stellt sich heraus, dass der Integrand die Größe der Warteschlange in Stücken ist. Zweitens Zeile für Zeile - einfach die Latenz aller Anforderungen addieren. Es ist klar, dass beide Berechnungen die gleiche Fläche ergeben, daher sind sie gleich. Wenn beide Teile dieser Gleichheit durch die Zeit Δt geteilt werden, für die wir die Fläche berechnet haben, haben wir links die durchschnittliche Warteschlangenlänge $$$L$ (per Definition des Durchschnitts). Rechts ist es etwas kniffliger. Wir müssen dem Zähler und Nenner eine weitere Anzahl von Anforderungen N hinzufügen, dann werden wir erfolgreich sein

$$

$$\ frac {\ sum W_i} {\ Delta t} = \ frac {\ sum W_i} {N} \ frac {N} {\ Delta t} = W \ lambda$$

Wenn wir ein ausreichend großes Δt oder eine Beschäftigungsdauer betrachten, werden die Fragen an den Rändern entfernt und der Satz kann als bewiesen betrachtet werden.

Es ist wichtig zu sagen, dass wir im Beweis keine Verteilungen von Wahrscheinlichkeiten verwendet haben. Tatsächlich ist der Satz von Little ein deterministisches Gesetz! Solche Gesetze werden in der Warteschlangentheorie des Betriebsrechts genannt. Sie können auf beliebige Teile des Systems und auf beliebige Verteilungen verschiedener Zufallsvariablen angewendet werden. Diese Gesetze bilden einen Konstruktor, mit dem Durchschnittswerte in Netzwerken erfolgreich analysiert werden können. Der Nachteil ist, dass sie alle nur für Durchschnittswerte gelten und kein Wissen über die Verteilungen liefern.

Um auf die Frage zurückzukommen, warum der Satz von Little nicht auf Bytes angewendet werden kann, nehmen wir an, dass $$$A (t)$ und $$$D (t)$ Jetzt werden sie nicht in Stücken, sondern in Bytes gemessen. Wenn wir dann ein ähnliches Argument führen, erhalten wir stattdessen $$$W$ Das Seltsame ist der Bereich geteilt durch die Gesamtzahl der Bytes. Es sind immer noch Sekunden, aber es ist eine gewichtete durchschnittliche Latenz, bei der größere Anforderungen mehr Gewicht erhalten. Dieser Wert kann als durchschnittliche Latenz des Bytes bezeichnet werden - was im Allgemeinen logisch ist, da wir Teile durch Bytes ersetzt haben -, jedoch nicht als Latenz der Anforderung.

Der Satz von Little besagt, dass bei einem bestimmten Anforderungsstrom die Antwortzeit und die Anzahl der Anforderungen im System proportional sind. Wenn alle Anforderungen gleich aussehen, kann die durchschnittliche Antwortzeit nicht reduziert werden, ohne die Leistung zu erhöhen. Wenn wir die Größe der Abfragen im Voraus kennen, können wir versuchen, sie im Inneren neu anzuordnen, um den Bereich dazwischen zu verkleinern $$$A (t)$ und $$$D (t)$ und daher die durchschnittliche Systemantwortzeit. Wenn wir diese Idee fortsetzen, können wir beweisen, dass die Algorithmen für die kürzeste Verarbeitungszeit und die kürzeste verbleibende Verarbeitungszeit eine minimale durchschnittliche Antwortzeit für einen Server ergeben, ohne dass die Möglichkeit besteht, sich damit zu verdrängen. Es gibt jedoch einen Nebeneffekt: Große Anfragen werden möglicherweise nicht auf unbestimmte Zeit bearbeitet. Das Phänomen wird als „Hunger“ bezeichnet und steht in engem Zusammenhang mit dem Konzept der Fairness der Planung, das aus einem früheren Planungsbeitrag gelernt werden kann : Mythen und Realität .

Es gibt eine weitere häufige Falle, die mit dem Verständnis des Little'schen Gesetzes verbunden ist. Es gibt einen Single-Threaded-Server, der Benutzeranforderungen bearbeitet. Angenommen, wir haben irgendwie L gemessen - die durchschnittliche Anzahl von Anforderungen in der Warteschlange für diesen Server und S - die durchschnittliche Zeit, die der Server eine Anforderung bedient hat. Betrachten Sie nun eine neue eingehende Anfrage. Im Durchschnitt sieht er L-Anfragen vor sich. Das Servieren dauert durchschnittlich S Sekunden. Es stellt sich heraus, dass die durchschnittliche Wartezeit $$$W = L S$ . Aber nach dem Theorem stellt sich heraus, dass $$$W = L / \ lambda$ . Wenn wir die Ausdrücke gleichsetzen, sehen wir den Unsinn: $$$S = 1 / \ lambda$ . Was ist falsch an dieser Argumentation?

1. Das erste, was auffällt: Die Reaktionszeit nach dem Theorem hängt nicht von S ab. Tatsächlich natürlich. Es ist nur so, dass die durchschnittliche Warteschlangenlänge dies bereits berücksichtigt: Je schneller der Server, desto kürzer die Warteschlangenlänge und desto kürzer die Antwortzeit.
2. Wir betrachten ein System, in dem sich Warteschlangen nicht für immer ansammeln, sondern regelmäßig zurückgesetzt werden. Dies bedeutet, dass die Serverauslastung weniger als 100% beträgt und wir alle eingehenden Anforderungen überspringen, und zwar mit der gleichen Durchschnittsgeschwindigkeit, mit der diese Anforderungen eingegangen sind. Dies bedeutet, dass die Verarbeitung einer einzelnen Anforderung im Durchschnitt nicht S Sekunden dauert, sondern mehr $$$1 / \ lambda$ Sekunden, einfach weil wir manchmal keine Anfragen bearbeiten. Tatsache ist, dass in jedem stabilen offenen System ohne Verlust der Durchsatz nicht von der Geschwindigkeit der Server abhängt, sondern nur vom Eingabestream bestimmt wird.
3. Die Annahme, dass eine eingehende Anforderung im System eine zeitlich durchschnittliche Anzahl von Anforderungen sieht, ist nicht immer wahr. Gegenbeispiel: Eingehende Anfragen kommen regelmäßig und wir können jede Anfrage bearbeiten, bevor die nächste eintrifft. Ein typisches Bild für Echtzeitsysteme. Eine eingehende Anforderung sieht immer keine Anforderungen im System, aber im Durchschnitt hat das System offensichtlich mehr als null Anforderungen. Wenn die Anfragen zu völlig zufälligen Zeiten kommen, "sehen sie wirklich die durchschnittliche Anzahl von Anfragen".
   
   
   
4. Wir haben nicht berücksichtigt, dass mit einer bestimmten Wahrscheinlichkeit möglicherweise bereits eine Anforderung auf dem Server vorhanden ist, die "erweitert" werden muss. Im allgemeinen Fall unterscheidet sich die durchschnittliche Zeit nach dem Service von der anfänglichen Servicezeit, und manchmal kann sie sich paradoxerweise als viel länger herausstellen. Wir werden am Ende auf dieses Thema zurückkommen, wenn wir über Mikrobursts sprechen. Bleiben Sie dran.

Der Satz von Little kann also auf große und kleine Systeme, auf Warteschlangen, auf Server und auf einzelne Verarbeitungsthreads angewendet werden. In all diesen Fällen werden Anfragen normalerweise auf die eine oder andere Weise klassifiziert. Anfragen verschiedener Benutzer, Anfragen unterschiedlicher Prioritäten, Anfragen von verschiedenen Standorten oder Anfragen verschiedener Typen. In diesem Fall sind nach Klassen aggregierte Informationen nicht interessant. Ja, die durchschnittliche Anzahl gemischter Anfragen und die durchschnittliche Antwortzeit für alle sind wiederum proportional. Was aber, wenn wir die durchschnittliche Antwortzeit für eine bestimmte Klasse von Anfragen wissen möchten? Überraschenderweise kann der Satz von Little auf eine bestimmte Klasse von Abfragen angewendet werden. In diesem Fall müssen Sie als nehmen $$$\ lambda$ Die Rate, mit der diese Klasse nicht alle anfordert. Als $$$L$ und $$$W$ - Durchschnittswerte der Anzahl und Verweilzeit von Anfragen dieser Klasse im untersuchten Teil des Systems.

Offene und geschlossene Systeme

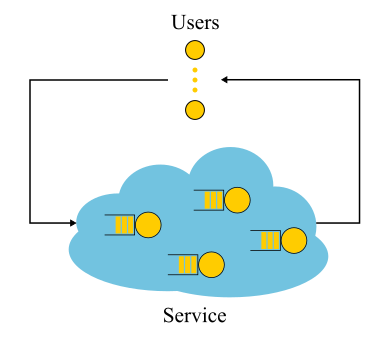
Es ist erwähnenswert, dass für geschlossene Systeme die „falsche“ Argumentationslinie zur Schlussfolgerung führt $$$S = 1 / \ lambda$ stellt sich als wahr heraus. Geschlossene Systeme sind Systeme, in denen Anforderungen nicht von außen kommen und nicht nach außen gehen, sondern von innen zirkulieren. Oder andernfalls Feedback-Systeme: Sobald die Anfrage das System verlässt, tritt eine neue Anfrage an ihre Stelle. Diese Systeme sind auch wichtig, da jedes offene System als in ein geschlossenes System eingetaucht betrachtet werden kann. Sie können die Site beispielsweise als offenes System betrachten, in dem Anfragen ständig eingegossen, verarbeitet und zurückgezogen werden, oder im Gegenteil als geschlossenes System zusammen mit der gesamten Zielgruppe der Site. Dann sagen sie normalerweise, dass die Anzahl der Benutzer festgelegt ist, und warten entweder auf eine Antwort auf die Anfrage oder „denken“: Sie haben ihre Seite erhalten und noch nicht auf den Link geklickt. Für den Fall, dass die Denkzeit immer Null ist, wird das System auch als Batch-System bezeichnet.

Das Little'sche Gesetz für geschlossene Systeme gilt für die Geschwindigkeit externer Ankünfte $$$\ lambda$ (Sie befinden sich nicht in einem geschlossenen System) Ersetzen Sie sie durch die Systembandbreite. Wenn wir den oben beschriebenen Single-Threaded-Server in ein Batch-System einbinden, erhalten wir $$$S = 1 / \ lambda$ und 100% Recycling. Oft führt ein solcher Blick auf das System zu unerwarteten Ergebnissen. In den 90er Jahren gab genau diese Sicht des Internets zusammen mit den Benutzern als einem einzigen System den Anstoß für die Untersuchung anderer als exponentieller Verteilungen. Wir werden die Verteilungen weiter diskutieren, aber hier stellen wir fest, dass zu dieser Zeit fast alles und überall als exponentiell angesehen wurde, und dies wurde sogar als Rechtfertigung und nicht nur als Entschuldigung im Sinne von "ansonsten zu kompliziert" angesehen. Es stellte sich jedoch heraus, dass nicht alle praktisch wichtigen Verteilungen gleich lange Schwänze haben und dass Kenntnisse über Verteilungsschwänze erprobt werden können. Aber jetzt kehren wir zu den Durchschnittswerten zurück.

Relativistische Effekte

Angenommen, wir haben ein offenes System: ein komplexes Netzwerk oder einen einfachen Single-Threaded-Server - das spielt keine Rolle. Was ändert sich, wenn wir das Eintreffen von Anfragen verdoppeln und deren Verarbeitung um die Hälfte beschleunigen - beispielsweise durch Verdoppelung der Kapazität aller Systemkomponenten? Wie ändern sich Auslastung, Durchsatz, durchschnittliche Anzahl von Anforderungen im System und durchschnittliche Antwortzeit? Bei einem Single-Threaded-Server können Sie versuchen, die Formeln zu übernehmen, sie "Stirn" anzuwenden und die Ergebnisse zu erhalten. Was tun Sie jedoch mit einem beliebigen Netzwerk? Die intuitive Lösung lautet wie folgt. Angenommen, die Zeit wird verdoppelt, dann scheinen sich in unserem „beschleunigten Referenzsystem“ die Geschwindigkeit der Server und der Fluss der Anforderungen nicht zu ändern. Dementsprechend haben alle Parameter in der beschleunigten Zeit die gleichen Werte wie zuvor. Mit anderen Worten entspricht die Beschleunigung aller "beweglichen Teile" eines Systems der Beschleunigung der Uhr. Jetzt konvertieren wir die Werte in ein System mit einer normalen Zeit. Dimensionslose Mengen (Auslastung und durchschnittliche Anzahl von Anfragen) ändern sich nicht. Werte, deren Dimension Zeitfaktoren ersten Grades enthält, variieren proportional. Der Durchsatz von [Anfragen / s] wird verdoppelt und die Antwort- und Wartezeiten [s] werden halbiert.

Dieses Ergebnis kann auf zwei Arten interpretiert werden:

1. Ein System, das um das k-fache beschleunigt wurde, kann den Aufgabenfluss k-mal mehr und mit einer durchschnittlichen Antwortzeit k-mal weniger verdauen.
2. Wir können sagen, dass sich die Leistung nicht geändert hat, sondern einfach die Größe der Aufgaben um das k-fache verringert hat. Es stellt sich heraus, dass wir die gleiche Ladung an das System senden, aber in kleinere Stücke zersägt. Und ... oh, ein Wunder! Die durchschnittliche Reaktionszeit wird reduziert!

Ich stelle erneut fest, dass dies für eine breite Klasse von Systemen gilt und nicht nur für einen einfachen Server. Aus praktischer Sicht gibt es nur zwei Probleme:

1. Nicht alle Teile des Systems können leicht beschleunigt werden. Wir können einige überhaupt nicht beeinflussen. Zum Beispiel die Lichtgeschwindigkeit.
2. Nicht alle Aufgaben können unendlich in immer kleinere Aufgaben unterteilt werden, da nicht gelernt wurde, Informationen in Teilen von weniger als einem Bit zu übertragen.

Betrachten Sie den Übergang zur Grenze. Angenommen, im gleichen offenen System Interpretation Nr. 2. Wir teilen jede eingehende Anfrage in zwei Hälften. Die Reaktionszeit ist ebenfalls in zwei Hälften geteilt. Wiederholen Sie die Teilung viele Male. Und wir müssen nicht einmal etwas im System ändern. Es stellt sich heraus, dass Sie die Antwortzeit beliebig verkürzen können, indem Sie eingehende Anforderungen einfach in eine ausreichend große Anzahl von Teilen zersägen. Im Limit können wir sagen, dass wir anstelle von Abfragen eine „Abfrageflüssigkeit“ erhalten, die wir von unseren Servern filtern. Dies ist das sogenannte Fluidmodell, ein sehr praktisches Werkzeug zur vereinfachten Analyse. Aber warum ist die Reaktionszeit Null? Was ist schief gelaufen? Wo haben wir die Latenz nicht berücksichtigt? Es stellt sich heraus, dass wir nicht nur die Lichtgeschwindigkeit berücksichtigt haben, sondern dass sie nicht verdoppelt werden kann. Die Laufzeit im Netzwerkkanal kann nicht geändert werden, Sie können es nur ertragen. Tatsächlich umfasst die Übertragung über ein Netzwerk zwei Komponenten: Übertragungszeit und Laufzeit. Die erste kann durch Erhöhen der Leistung (Kanalbreite) oder Verringern der Größe von Paketen beschleunigt werden, und die zweite ist sehr schwer zu beeinflussen. In unserem „Flüssigkeitsmodell“ gab es einfach keine Reservoire für die Ansammlung von Flüssigkeiten - Netzwerkkanäle mit ungleich Null und konstanten Ausbreitungszeiten. Wenn wir sie zu unserem „Flüssigkeitsmodell“ hinzufügen, wird die Latenz übrigens durch die Summe der Ausbreitungszeiten bestimmt, und die Warteschlangen in den Knoten sind immer noch leer. Warteschlangen hängen nur von der Paketgröße und der Variabilität (Leseburst) des Eingabestreams ab.

Daraus folgt, dass Sie bei der Latenz nicht mit der Berechnung von Durchflüssen auskommen können und selbst Recyclinggeräte nicht alles lösen. Es ist notwendig, die Größe der Anforderungen zu berücksichtigen und die Verteilungszeit nicht zu vergessen, die in der Warteschlangentheorie häufig ignoriert wird, obwohl das Hinzufügen zu den Berechnungen überhaupt nicht schwierig ist.

Verteilungen

Was ist der Grund für die Warteschlange? Offensichtlich hat das System nicht genügend Kapazität und der Überschuss an Anfragen sammelt sich an? Nicht wahr! Warteschlangen treten auch in Systemen auf, in denen genügend Ressourcen vorhanden sind. Wenn nicht genügend Kapazität vorhanden ist, ist das System, wie Theoretiker sagen, nicht stabil. Es gibt zwei Hauptgründe für das Anstehen: die Unregelmäßigkeit von Anforderungen und die Variabilität der Größe von Anforderungen. Wir haben bereits ein Beispiel untersucht, in dem beide Gründe beseitigt wurden: ein Echtzeitsystem, bei dem Anfragen gleicher Größe streng regelmäßig eingehen. Eine Warteschlange bildet sich nie. Die durchschnittliche Wartezeit in der Warteschlange beträgt Null. , , , . , .

A/S/k/K, A — , S — , k — , K — (, ). , M/M/1 : M (Markovian Memoryless) , . : $$$\lambda$ — — , : . M , μ . , , . , 4- . , , : G — (, , ), D — deterministic. C — D/D/1. , 1909 ., — M/D/1. — M/G/k k>1, M/G/1 1930-.

?

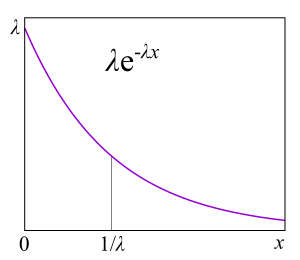
, , , , , . , . , failure rate . , , : , . failure rate function, . , «» , . , : , . , failure rate — , , - , — . , , , , , . « ».

Failure rate . — . Failure rate , , , . failure rate, , , . failure rate, , , . , , , software hardware? : ? . , , - . ? , — . ( failure rate) . « » .

, , failure rate, , , unix- . , .

RTMR , . LWTrace - . . , . , $$$\mathbf{P}\{S>x\}$ . , failure rate , , : .



$$$\mathbf{P}\{S>x\} = x^{-a}$ , — . , « », 80/20: , . . , . , RTMR -, , . Parameter $$$a=1.16$ , 80/20: 20% 80% .

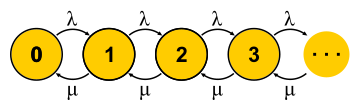
, . . , , , - . , — . « » , « » — . : , ? , ( , ), . , 0 . , , $$$\mu N_1$ $$$\lambda N_0$ . , , — . . , . M/M/1 $$$\mathbf{P}\{Q=i\} = (1 - \rho) \rho^i$ wo $$$\rho = \lambda / \mu$ - Dies ist die Serverauslastung. Das Ende der Geschichte. Im Verlauf der Präsentation habe ich eine anständige Anzahl von Annahmen übersehen und einige Substitutionen von Konzepten vorgenommen, aber die Essenz hat hoffentlich nicht gelitten.

Es ist wichtig zu verstehen, dass dieser Ansatz nur funktioniert, wenn der aktuelle Zustand der Maschine ihr weiteres Verhalten vollständig bestimmt und die Geschichte, wie sie in diesen Zustand gelangt ist, nicht wichtig ist. Für das alltägliche Verständnis einer endlichen Zustandsmaschine ist dies selbstverständlich - schließlich ist es eine Bedingung dafür. Für einen stochastischen Prozess folgt daraus jedoch, dass alle Verteilungen exponentiell sein müssen, da nur sie keinen Speicher haben - sie haben eine konstante Ausfallrate.

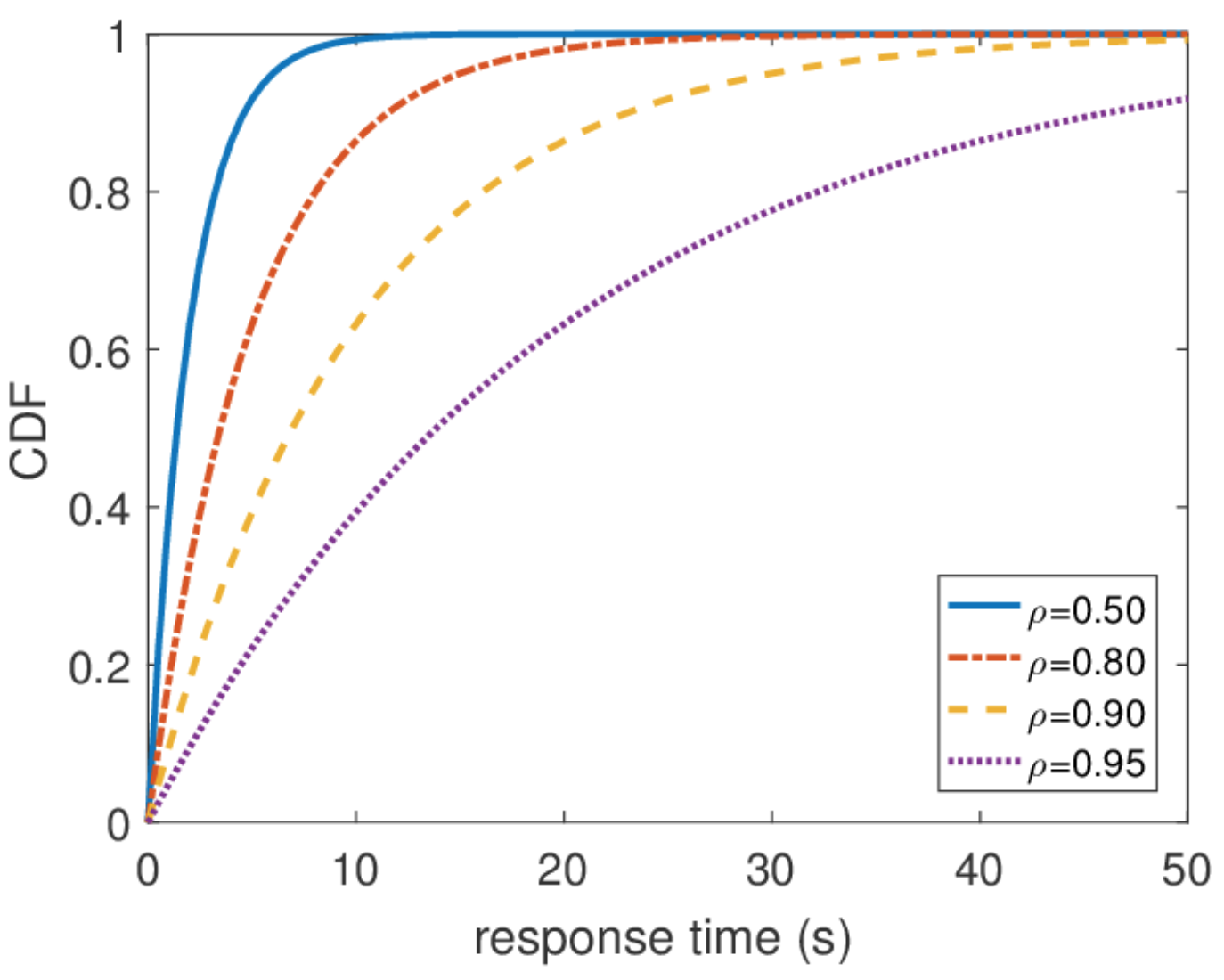
Es ist auch wichtig zu sagen, dass alle anderen Informationen über das System leicht zu erhalten sind, wenn wir die Gleichgewichtsverteilung kennen. Die durchschnittliche Anzahl von Abfragen im System ist der Durchschnitt dieser Verteilung. Um die durchschnittliche Antwortzeit zu ermitteln, wenden wir den Satz von Little auf die Anzahl der Abfragen an. Die Verteilung der Antwortzeit ist etwas schwieriger zu finden, aber auch in einigen Aktionen können Sie dies herausfinden $$$\ mathbf {P} \ {response \ _time> t \} = e ^ {- (\ mu- \ lambda) t}$ und was ist die durchschnittliche Antwortzeit $$$1 / (\ mu- \ lambda)$ .

Unbegrenzte Reaktionszeit

Aus dieser Verteilung können Sie jedes Perzentil der Antwortzeit ermitteln, und es stellt sich heraus, dass das hundertste Perzentil gleich unendlich ist. Mit anderen Worten, die schlechteste Antwortzeit ist nicht von oben begrenzt. Was im Allgemeinen nicht überraschend ist, da wir den Poisson-Stream verwendet haben. In der Praxis kann ein solches Verhalten jedoch niemals erreicht werden. Offensichtlich ist der Eingabestrom von Anforderungen an den Server begrenzt, zumindest durch die Breite des Netzwerkkanals zu diesem Server, und die Warteschlangenlänge wird durch den Speicher auf diesem Server begrenzt. Der Poisson-Strom hingegen garantiert mit einer Wahrscheinlichkeit ungleich Null das Auftreten beliebig großer Bursts. Daher würde ich nicht empfehlen, beim Entwurf eines Systems von der Annahme eines Poisson-Eingabestreams auszugehen, wenn Sie an hohen Perzentilen interessiert sind und die Systemlast sehr hoch ist. Es ist besser, andere Verkehrsmodelle zu verwenden, über die ich ein anderes Mal sprechen werde, wenn ich über Netzwerkrechnung spreche.

Skalierung und Garantien

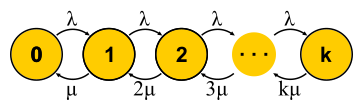
Jetzt, da wir über ausreichend leistungsfähige Möglichkeiten zur Analyse von Systemen verfügen, können wir versuchen, diese auf verschiedene Aufgaben anzuwenden und die Vorteile zu nutzen. So entwickelte sich die Theorie des Massendienstes in der zweiten Hälfte des 20. Jahrhunderts. Versuchen wir zu verstehen, was erreicht wurde. Kehren wir zunächst zu den Aufgaben zurück, die Erlang gelöst hat. Dies sind die Aufgaben M / M / k / k und M / M / k, bei denen wir die Ausfallwahrscheinlichkeit begrenzen möchten. Es stellt sich heraus, dass es für sie nicht schwierig ist, Markov-Ketten zu konstruieren. Der Unterschied besteht darin, dass mit dem Hinzufügen von Aufgaben die Wahrscheinlichkeit eines umgekehrten Übergangs zunimmt, da Aufgaben parallel verarbeitet werden. Wenn jedoch die Anzahl der Aufgaben der Anzahl der Server entspricht, tritt eine Sättigung auf. Ferner endet für M / M / k / k das Netzwerk, der Automat stellt sich wirklich als endlich heraus und alle Anforderungen, die in den letzten Zustand gelangen, werden abgelehnt. Die Wahrscheinlichkeit dieses Ereignisses ist einfach gleich der Wahrscheinlichkeit, dass wir uns im letzten Zustand befinden.

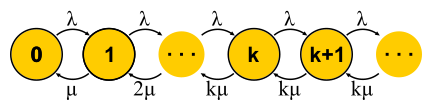
Bei M / M / k ist die Situation komplizierter, Anforderungen werden in die Warteschlange gestellt, neue Status werden angezeigt, aber die Wahrscheinlichkeit eines umgekehrten Übergangs steigt nicht - alle Server arbeiten bereits. Das Netzwerk wird unendlich, wie bei M / M / 1. Übrigens, wenn die Anzahl der Anforderungen im System begrenzt ist, hat die Kette immer eine endliche Anzahl von Zuständen und auf die eine oder andere Weise wird sie gelöst, was über die endlosen Ketten nicht gesagt werden kann. In geschlossenen Systemen sind die Ketten immer endlich. Durch Lösen der für M / M / k / k und M / M / k beschriebenen Schaltungen erhalten wir die Formel B bzw. die Erlang- Formel C. Sie sind ziemlich sperrig, ich werde sie nicht geben, aber mit ihrer Hilfe können Sie ein interessantes Ergebnis für die Entwicklung der Intuition erzielen, die als Quadratwurzel-Personalregel bezeichnet wird. Angenommen, es gibt ein M / M / k-System mit einem gegebenen Eingangsstrom λ von Anforderungen pro Sekunde. Angenommen, die Last sollte sich bis morgen verdoppeln. Die Frage ist: Wie kann die Anzahl der Server erhöht werden, damit die Antwortzeit gleich bleibt? Die Anzahl der Server muss verdoppelt werden, oder? Es stellt sich überhaupt nicht heraus. Denken Sie daran, dass wir bereits gesehen haben: Wenn Sie die Zeit (Server und Anmeldung) um die Hälfte beschleunigen, verringert sich die durchschnittliche Antwortzeit um die Hälfte. Mehrere langsame und ein schneller Server sind nicht dasselbe, aber die Rechenleistung ist gleich. Insbesondere für M / M / 1 ist beispielsweise die Reaktionszeit umgekehrt proportional zum Volumen der "freien Kapazität" $$$\ mu - \ lambda$ und wird nur durch dieses Volumen bestimmt. Wenn sowohl der Durchfluss als auch die Verarbeitungsleistung verdoppelt werden, verdoppelt sich die freie Kapazität des Systems: $$$2 \ mu - 2 \ lambda$ . Es scheint, dass Sie zur Lösung des Problems nur die freie Kapazität speichern müssen, aber die Antwortzeit in M ​​/ M / k wird bereits durch die komplexere Erlang-Formel bestimmt. Es stellt sich heraus, dass die freie Kapazität proportional zur Quadratwurzel der Anzahl der "ausgelasteten Server" beibehalten werden muss, um die gleiche Antwortzeit aufrechtzuerhalten. Mit der Anzahl der "ausgelasteten Server" ist die Gesamtzahl der Server multipliziert mit der Auslastung gemeint: Dies ist die Mindestanzahl von Servern, die für einen stabilen Betrieb erforderlich sind.

Mit dieser Regel versuchen sie manchmal zu rechtfertigen, wie ein Cluster mit Servern erweitert werden kann. Machen Sie sich jedoch nicht die Illusion, dass ein Cluster ein M / M / k-System ist. Wenn Sie beispielsweise einen Balancer an Ihrer Eingabe haben, der Anforderungen in Warteschlangen an Server sendet, ist dies nicht mehr M / M / k, da M / M / k eine gemeinsame Warteschlange impliziert, aus der Server Anforderungen abrufen, wenn sie freigegeben werden. Dieses Modell eignet sich jedoch beispielsweise für Thread-Pools mit einer gemeinsamen FIFO-Warteschlange. Selbst in diesem Fall ist jedoch zu beachten, dass diese Regel eine Annäherung für den Fall darstellt, dass viele Threads vorhanden sind. Wenn Sie mehr als 10 Threads haben, können Sie davon ausgehen, dass es viele davon gibt. Vergessen Sie nicht die allgegenwärtigen Exponentialverteilungen: Ohne die Exponentialität aller Verteilungen anzunehmen, funktioniert die Regel auch nicht.

Netzwerkantwortzeit

Letztendlich ist ein Netzwerk von M / M / k von Interesse, das zumindest in einer Kette verbunden ist, da wir verteilte Systeme herstellen. Um Netzwerke zu studieren, hätte ich gerne einen Konstruktor: einfache und klare Regeln zum Verbinden bekannter Elemente zu Blöcken. In der Steuerungstheorie gibt es beispielsweise Übertragungsfunktionen, die verständlicherweise mit seriellen oder parallelen Verbindungen kombiniert werden. Hier hat der Ausgangsstrom von jedem Knoten eine sehr komplizierte Verteilung, mit Ausnahme von M / M / k, das nach dem bekannten Burke-Theorem einen unabhängigen Poisson-Strom erzeugt. Diese Ausnahme wird, wie Sie sich vorstellen können, hauptsächlich verwendet.

Die Verbindung zweier Poisson-Streams ist ein Poisson-Stream. Die probabilistische Trennung des Poisson-Stroms in zwei ergibt wiederum zwei Poisson-Ströme. All dies führt dazu, dass alle Warteschlangen im System wie unabhängig voneinander sind und Sie in einer formalen Sprache die sogenannte Produktformlösung erhalten können . Das heißt, die gemeinsame Verteilung der Längen der Warteschlangen ist einfach das Produkt der Längenverteilungen aller Warteschlangen, die separat betrachtet werden - so wird Unabhängigkeit in der Wahrscheinlichkeitstheorie ausgedrückt. Wir finden nur die Eingabeflüsse zu allen Knoten und verwenden die Formeln für jeden Knoten unabhängig. Es gibt eine Reihe von Einschränkungen:

1. Probabilistischer Routing-Algorithmus. Die vom Knoten bediente Anforderung wählt die nächste zufällig mit einer bekannten Wahrscheinlichkeit aus. Dies ist nicht so schlimm, wie es scheinen mag, da es möglich ist, "Anforderungsklassen" zu verwenden: zu sagen, dass alle Vasya-Anforderungen an Server Nr. 1, dann an Server Nr. 2 und dann aus dem Netzwerk gehen und Petys Anforderungen an Server Nr. 2 gehen und dann mit gleicher Wahrscheinlichkeit Server Nummer 1 oder Nummer 3 besuchen und beenden. Das heißt, nicht alle Übergänge müssen zufällig sein, einige oder sogar alle haben möglicherweise eine 100% ige Wahrscheinlichkeit.
2. Kleinrocks Unabhängigkeitsannahme. Die Anforderungsverarbeitungszeit kann nicht vom Verlauf oder der Klasse der Anforderung abhängen, sondern wird nur vom Server bestimmt. Wenn die Anforderung erneut denselben Server durchläuft, wird sie jedes Mal zufällig ausgewählt. Tatsächlich gibt es keine Möglichkeit, die Größe der Anforderung festzulegen, die auf verschiedenen Servern verwendet werden würde, und die Servicezeit wird nur vom Server selbst bestimmt. Sie können auch versuchen, diese Einschränkung zu umgehen. Zu diesem Zweck wird normalerweise probabilistisches Routing verwendet, und es wird eine Schleife erstellt, um mit einiger Wahrscheinlichkeit zum selben Server zurückzukehren - als ob sie die Anforderung neu starten würden. Meiner Meinung nach ist dies ein ziemlich seltsamer Trick, da eine solche Anforderung erneut in die Warteschlange gestellt wird und nicht sofort ausgeführt wird, aber für einige Aufgaben ist dies nicht wichtig.
3. Poisson-Eingabeverkehr und exponentielle Servicezeit auf allen Knoten.

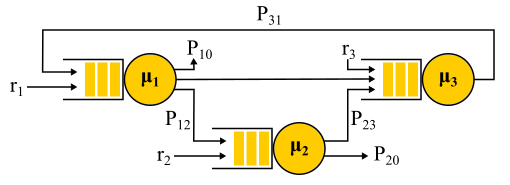
Jackson Network Beispiel.

Es ist erwähnenswert, dass bei Vorhandensein von Rückkopplung KEIN Poisson-Strom erhalten wird, da sich herausstellt, dass die Flüsse voneinander abhängig sind. Am Ausgang des Rückkopplungsknotens wird auch ein Nicht-Poisson-Strom erhalten, und als Ergebnis werden alle Flüsse Nicht-Poisson. Auf überraschende Weise stellt sich jedoch heraus, dass sich alle diese Nicht-Poisson-Flüsse genauso verhalten wie Poisson-Flüsse (oh, diese Wahrscheinlichkeitstheorie), wenn die obigen Einschränkungen erfüllt sind. Und dann bekommen wir wieder eine Produktformlösung. Solche Netzwerke werden als Jackson-Netzwerke bezeichnet . Sie können Feedback geben und daher mehrere Besuche auf jedem Server ermöglichen. Es gibt andere Netzwerke, in denen mehr Freiheiten erlaubt sind, aber infolgedessen beinhalten alle bedeutenden analytischen Errungenschaften der Warteschlangentheorie in Bezug auf Netzwerke Poisson-Ströme bei der Eingabe- und Produktformlösung, die Gegenstand der Kritik an dieser Theorie wurde und in den 90er Jahren dazu führte die Entwicklung anderer Theorien und die Untersuchung, welche Verteilung tatsächlich benötigt wird und wie man mit ihnen arbeitet.

Eine wichtige Anwendung dieser gesamten Theorie der Jackson-Netzwerke ist die Paketmodellierung in IP-Netzwerken und ATM-Netzwerken. Das Modell ist völlig ausreichend: Die Paketgrößen variieren nicht stark und hängen nicht vom Paket selbst ab, sondern nur von der Kanalbreite, da die Dienstzeit der Zeit entspricht, zu der das Paket an den Kanal gesendet wurde. Die zufällige Sendezeit ist zwar wild, weist jedoch keine sehr große Variabilität auf. Darüber hinaus stellt sich heraus, dass in einem Netzwerk mit deterministischer Servicezeit die Latenz nicht größer sein kann als in einem ähnlichen Jackson-Netzwerk, sodass solche Netzwerke sicher verwendet werden können, um die Antwortzeit von oben abzuschätzen.

Nicht exponentielle Verteilungen

Alle Ergebnisse, über die ich gesprochen habe, bezogen sich auf Exponentialverteilungen, aber ich erwähnte auch, dass reale Verteilungen unterschiedlich sind. Es besteht das Gefühl, dass diese ganze Theorie ziemlich nutzlos ist. Dies ist nicht ganz richtig. Es gibt eine Möglichkeit, andere Verteilungen in diesen mathematischen Apparat zu integrieren, außerdem praktisch alle Verteilungen, aber es wird uns etwas kosten. Mit Ausnahme einiger interessanter Fälle geht die Möglichkeit verloren, eine Lösung in expliziter Form zu erhalten, die Produktformlösung und damit der Konstruktor: Jedes Problem muss mit Markov-Ketten von Grund auf neu gelöst werden. Für die Theorie ist dies ein großes Problem, aber in der Praxis bedeutet es einfach die Anwendung numerischer Methoden und ermöglicht es, viel komplexere und realitätsnahe Probleme zu lösen.

Phasenmethode

Die Idee ist einfach. Markov-Ketten erlauben es uns nicht, Speicher in einem Zustand zu haben, daher sollten alle Übergänge zufällig sein und eine exponentielle Zeitverteilung zwischen zwei Übergängen aufweisen. Was aber, wenn der Staat in mehrere Unterzustände aufgeteilt ist? Die Übergänge zwischen Unterzuständen müssen immer noch exponentiell verteilt sein, wenn die gesamte Struktur eine Markov-Kette bleiben soll, und das wollen wir wirklich, weil wir wissen, wie man solche Ketten löst. Unterzustände werden oft als Phasen bezeichnet, wenn sie in Reihe angeordnet sind, und der Partitionsprozess wird als Phasenmethode bezeichnet.

Das einfachste Beispiel. Die Anfrage wird in mehreren Phasen verarbeitet: Zuerst lesen wir beispielsweise die erforderlichen Daten aus der Datenbank, führen dann einige Berechnungen durch und schreiben die Ergebnisse in die Datenbank. Angenommen, alle diese drei Stufen haben dieselbe exponentielle Zeitverteilung. Welche Verteilung hat die Laufzeit aller drei Phasen zusammen? Dies ist die Verteilung von Erlang.



Aber was ist, wenn Sie viele, viele kurze identische Phasen machen? Im Limit erhalten wir eine deterministische Verteilung. Das heißt, durch den Aufbau einer Kette können Sie die Variabilität der Verteilung verringern.

Ist es möglich, die Variabilität zu erhöhen? Einfach. Anstelle einer Phasenkette verwenden wir alternative Kategorien und wählen zufällig eine davon aus. Ein Beispiel. Fast alle Anforderungen werden schnell ausgeführt, aber es besteht eine geringe Wahrscheinlichkeit, dass eine große Anforderung eingeht, was lange dauert. Eine solche Verteilung hat eine abnehmende Ausfallrate. Je länger wir warten, desto wahrscheinlicher ist es, dass die Anfrage in die zweite Kategorie fällt.



Bei der Weiterentwicklung der Phasenmethode haben Theoretiker festgestellt, dass es eine Klasse von Verteilungen gibt, mit denen Sie sich einer beliebigen nicht negativen Verteilung mit beliebiger Genauigkeit nähern können! Die Coxsche Verteilung wird nach der Phasenmethode aufgebaut, nur müssen wir nicht alle Phasen durchlaufen, nach jeder Phase besteht eine gewisse Wahrscheinlichkeit der Fertigstellung.



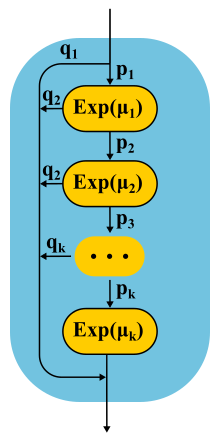
Diese Art der Verteilung kann sowohl zum Generieren eines Nicht-Poisson-Eingabestreams als auch zum Erstellen einer nicht exponentiellen Servicezeit verwendet werden. Hier ist zum Beispiel die Markov-Kette für das M / E2 / 1-System mit Erlang-Verteilung für die Servicezeit. Der Status wird durch ein Zahlenpaar (n, s) bestimmt, wobei n die Länge der Warteschlange und s die Nummer der Stufe ist, in der sich der Server befindet: erste oder zweite. Alle Kombinationen von n und s sind möglich. Eingehende Nachrichten ändern sich nur n, und nach Abschluss der Phasen wechseln sie sich ab und verringern die Länge der Warteschlange nach Abschluss der zweiten Phase.

Sie haben Mikrobursts!

Kann ein System mit der Hälfte seiner Kapazität langsamer werden? Als erste Testperson bereiten wir M / G / 1 vor. Gegeben: Poissonfluss am Einlass und willkürliche Verteilung der Servicezeit. Betrachten Sie den Pfad einer einzelnen Anforderung durch das gesamte System. Eine zufällig eingehende eingehende Anfrage sieht in der Warteschlange vor sich die durchschnittliche Zeitanzahl der Anfragen $$$\ mathbf {E} [N_Q]$ . Die durchschnittliche Verarbeitungszeit für jeden von ihnen $$$\ mathbf {E} [S]$ . Mit einer Wahrscheinlichkeit gleich Entsorgung $$$\ rho$ Es gibt eine weitere Anforderung auf dem Server, die zuerst rechtzeitig "bearbeitet" werden muss $$$\ mathbf {E} [S_e]$ . Zusammenfassend ergibt sich die Gesamtwartezeit in der Warteschlange $$$\ mathbf {E} [T_Q] = \ mathbf {E} [N_Q] \ mathbf {E} [S] + \ rho \ mathbf {E} [S_e]$ . Nach dem Satz von Little $$$\ mathbf {E} [N_Q] = \ lambda \ mathbf {E} [T_Q]$ ;; Kombinieren erhalten wir:

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ mathbf {E} [S_e]$$

Das heißt, die Wartezeit in der Warteschlange wird durch zwei Faktoren bestimmt. Der erste ist der Effekt der Servernutzung und der zweite ist die durchschnittliche After-Service-Zeit. Betrachten Sie den zweiten Faktor. Eine Anfrage, die irgendwann eintrifft $$$t$ sieht, dass Nachsorge Zeit braucht $$$S_e (t)$ .



Durchschnittliche Zeit $$$\ mathbf {E} [S_e]$ bestimmt durch den Durchschnittswert der Funktion $$$S_e (t)$ das heißt, die Fläche der Dreiecke geteilt durch die Gesamtzeit. Es ist klar, dass wir uns dann auf ein „mittleres“ Dreieck beschränken können $$$\ mathbf {E} [S_e] = \ mathbf {E} [S ^ 2] / 2 \ mathbf {E} [S]$ . Das ist ziemlich unerwartet. Wir haben erhalten, dass die Zeit nach dem Service nicht nur durch den Durchschnittswert der Servicezeit, sondern auch durch ihre Variabilität bestimmt wird. Die Erklärung ist einfach. Die Wahrscheinlichkeit, in ein langes Intervall zu fallen $$$S$ mehr noch ist es tatsächlich proportional zur Dauer S dieses Intervalls. Dies erklärt das berühmte Wartezeitparadoxon oder Inspektionsparadoxon. Aber zurück zu M / G / 1. Wenn Sie alles, was wir haben, kombinieren und mithilfe von Variabilität neu schreiben $$$C ^ 2_S = \ mathbf {E} [S] / \ mathbf {E} [S] ^ 2$ Holen Sie sich die berühmte Pollaczek-Khinchine-Formel :

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ frac {\ mathbf {E} [S]} {2} (C ^ 2_S + 1)$$

Wenn der Beweis Sie gelangweilt hat, hoffe ich, dass er dem Ergebnis seiner Anwendung in der Praxis gefällt. Wir haben bereits Servicezeitdaten in RTMR untersucht. Der lange Schwanz entsteht nur mit großer Variabilität, und in diesem Fall $$$C ^ 2_S = 381$ . Sie sehen, das ist viel mehr als $$$C ^ 2_S = 1$ für die Exponentialverteilung. Im Durchschnitt ist alles super schnell: $$$\ mathbf {E} [S] = 263,792 μs$ . Nehmen wir nun an, dass RTMR vom M / G / 1-System modelliert wird, und lassen Sie das System nicht stark belastet entsorgen $$$\ rho = 0,5$ . Wenn wir die Formel einsetzen, erhalten wir $$$\ mathbf {E} [T_Q] = 1 * (381 + 1) / 2 * 263,792 μs = 50 ms$ . Aufgrund von Mikrobursts kann sich selbst ein so schnelles und nicht ausgelastetes System im Durchschnitt in ein widerliches verwandeln. Für 50 ms können Sie 6 Mal auf die Festplatte oder, wenn Sie Glück haben, sogar in ein Rechenzentrum auf einem anderen Kontinent gehen! Übrigens gibt es für G / G / 1 eine Annäherung , die die Variabilität des eingehenden Verkehrs berücksichtigt: Sie sieht nur stattdessen genauso aus $$$C ^ 2_S + 1$ es ist die Summe beider Sorten $$$C ^ 2_S + C ^ 2_A$ . Bei mehreren Servern sind die Dinge besser, aber die Auswirkung mehrerer Server wirkt sich nur auf den ersten Faktor aus. Der Effekt der Variabilität bleibt: $$$\ mathbf {E} [T_Q] ^ {G / G / k} ≈ \ mathbf {E} [T_Q] ^ {M / M / k} (C ^ 2_S + C ^ 2_A) / 2$ .

Wie sieht Mikroburst aus? In Bezug auf Thread-Pools sind dies Aufgaben, die schnell genug ausgeführt werden, um in Recycling-Zeitplänen nicht sichtbar zu sein, und langsam genug, um eine Warteschlange hinter sich zu erstellen und die Antwortzeit des Pools zu beeinflussen. Aus theoretischer Sicht sind dies große Fragen vom Ende der Verteilung. Angenommen, Sie haben einen Pool von 10 Threads und sehen sich den Recycling-Zeitplan an, der auf den Metriken Betriebszeit und Ausfallzeit basiert, die alle 15 Sekunden erfasst werden. Zunächst einmal bemerken Sie möglicherweise nicht, dass ein Thread überhaupt hängt oder dass alle 10 Threads gleichzeitig große Aufgaben für eine Sekunde ausgeführt haben und dann 14 Sekunden lang nichts getan haben. Eine Auflösung von 15 Sekunden erlaubt keinen Auslastungssprung von bis zu 100% und zurück zu 0%, und die Reaktionszeit leidet. , , 15 6 , .



, ( ) .

, RTMR SelfPing, ( 10 ), — . , 10 15 . , . , , 10 , , — . self-ping- CPU. , : , , . : , , . : . , 15- , — .

, , SelfPing , ? ? , LWTrace. , . -100 . . : ; — , , ; perf , , .

« », . , , . FIFO-. , , latency ( SPT SRPT). — . , , , . , « », .

, - product-form solution . M/ Cox /1/ PS . , (Coxian distribution) (Processor Sharing), , , . ? , . , , (. ) , , M/ M /1/ FIFO , , .

! , , , ! insensitivity property. , , , , . — M/M/∞. , . , product-form solution — BCMP .

. , (, ), , , ó . . . $$$\mathbf{E}[T] = 1/3 \mathbf{E}[T_1] + 2/3 \mathbf{E}[T_2]$ . $$$\mathbf{E}[T_i] = 1/(\mu_i - \lambda_i)$ M/M/1/FCFS $$$\mathbf{E}[T] = 1/3 * 1/(3 - 3 * 1/3) + 2/3 * 1/(4 - 3*2/3) = 0.5$ .

, , . , .

1. , , , computer science, . Performance Modeling and Design of Computer Systems: Queueing Theory in Action (2013). - , . ó — .
2. , , , , Robert B. Cooper. , .