Die Tankabtastung (dt. "Reservoirabtastung") ist ein einfacher und effizienter Algorithmus zum zufälligen Abtasten einer bestimmten Anzahl von Elementen aus einem vorhandenen Vektor großer und / oder unbekannter Größe im Voraus. Ich habe auf Habré keinen Artikel über diesen Algorithmus gefunden und habe mich daher entschlossen, ihn selbst zu schreiben.
Also, wovon reden wir? Die Auswahl eines zufälligen Elements aus einem Vektor ist eine elementare Aufgabe:
Die Aufgabe, „K zufällige Elemente von einem Vektor der Größe N zurückzugeben“, ist bereits schwieriger. Hier können Sie bereits einen Fehler machen - nehmen Sie beispielsweise K erste Elemente (dies verletzt die Anforderung der Zufälligkeit) oder nehmen Sie jedes der Elemente mit der Wahrscheinlichkeit K / N (dies verletzt die Anforderung, genau K Elemente zu nehmen). Darüber hinaus ist es möglich, eine formal korrekte, aber äußerst ineffektive Lösung zu implementieren, "alle Elemente zufällig zu mischen und zuerst das K zu nehmen". Und alles wird noch interessanter, wenn wir die Bedingung hinzufügen, dass N eine sehr große Zahl ist (wir haben nicht genug Speicher, um alle N Elemente zu speichern) und / oder nicht im Voraus bekannt ist. Stellen Sie sich zum Beispiel vor, wir haben eine Art externen Dienst, der uns Elemente einzeln sendet. Wir wissen nicht, wie viele von ihnen insgesamt kommen werden, und wir können sie nicht alle speichern, aber wir möchten eine Reihe von genau K zufällig ausgewählten Elementen aus den Elementen haben, die zu einem bestimmten Zeitpunkt empfangen wurden.
Der Reservoir-Sampling-Algorithmus ermöglicht es uns, dieses Problem in O (N) -Schritten und O (K) -Speicher zu lösen. In diesem Fall ist es nicht erforderlich, N im Voraus zu kennen, und der Zustand der Zufallsstichprobe von genau K Elementen wird klar beobachtet.
Beginnen wir mit einer vereinfachten Aufgabe.
Sei K = 1, d.h. Wir müssen nur ein Element aus allen eingehenden Elementen auswählen - aber damit jedes der eingehenden Elemente die gleiche Wahrscheinlichkeit hat, ausgewählt zu werden. Der Algorithmus bietet sich an:
Schritt 1 : Ordnen Sie genau einem Element Speicher zu. Wir speichern darin das erste Element angekommen.

Bisher ist alles in Ordnung - nur ein Element ist zu uns gekommen, mit einer Wahrscheinlichkeit von 100% (im Moment) sollte es ausgewählt werden - es ist.
Schritt 2 : Das zweite eingehende Element wird mit einer Wahrscheinlichkeit von 1/2 als ausgewähltes Element neu geschrieben.

Auch hier ist alles in Ordnung: Bisher sind nur zwei Elemente zu uns gekommen. Der erste blieb mit einer Wahrscheinlichkeit von 1/2 ausgewählt, der zweite schrieb ihn mit einer Wahrscheinlichkeit von 1/2 um.
Schritt 3 : Das dritte eingehende Element mit einer Wahrscheinlichkeit von 1/3 wird als ausgewähltes Element neu geschrieben.
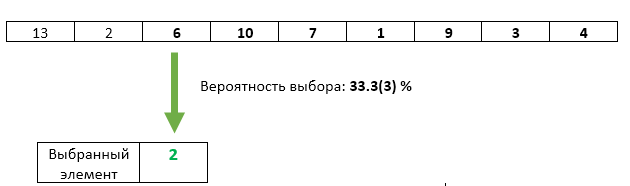
Mit dem dritten Element ist alles in Ordnung - die Chance, ausgewählt zu werden, beträgt genau 1/3. Aber haben wir in irgendeiner Weise die Chancengleichheit der vorherigen Elemente verletzt? Nein. Die Wahrscheinlichkeit, dass das ausgewählte Element in diesem Schritt nicht überschrieben wird, beträgt 1 - 1/3 = 2/3. Und da wir in Schritt 2 gleiche Chancen für jedes der auszuwählenden Elemente garantiert haben, kann nach Schritt 3 jedes mit einer Chance von 2/3 * 1/2 = 1/3 ausgewählt werden. Genau die gleiche Chance wie das dritte Element.
Schritt N : Mit einer Wahrscheinlichkeit von 1 / N wird die Elementnummer N als die ausgewählte umgeschrieben. Jeder der zuvor eingetroffenen Gegenstände hat die gleiche 1 / N-Chance, ausgewählt zu bleiben.
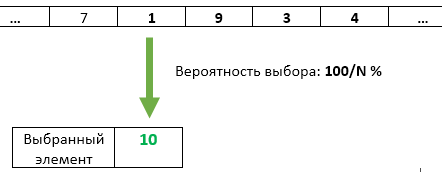
Aber es war eine vereinfachte Aufgabe mit K = 1.
Wie ändert sich der Algorithmus für K> 1?
Schritt 1 : Wir weisen K-Elementen Speicher zu. Wir schreiben darin die ersten K Elemente, die angekommen sind.

Die einzige Möglichkeit, K Elemente von K angekommenen Elementen zu nehmen, besteht darin, sie alle zu nehmen :)
Schritt N : (für jedes N> K): Erzeugen Sie eine Zufallszahl X von 1 bis N. Wenn X> K, verwerfen wir dieses Element und fahren mit dem nächsten fort. Wenn X <= K ist, schreiben Sie das Element mit der Zahl X um. Da der Wert von X im Bereich von 1 bis N gleichmäßig zufällig ist, ist er unter der Bedingung X <= K im Bereich von 1 bis K gleichmäßig zufällig. Somit stellen wir die Gleichmäßigkeit sicher Auswahl wiederbeschreibbarer Artikel.

Wie Sie sehen können, hat jedes nächste Element eine immer geringere Chance, ausgewählt zu werden. Trotzdem wird es immer genau K / N sein (wie für jedes der zuvor angekommenen Elemente).
Der Vorteil dieses Algorithmus ist, dass wir jederzeit anhalten und dem Benutzer den aktuellen Vektor K anzeigen können - und dies ist der Vektor ehrlich ausgewählter zufälliger Elemente aus der Folge der eingetroffenen Elemente. Vielleicht passt dies zum Benutzer, oder er möchte die eingehenden Werte weiter verarbeiten - wir können dies jederzeit tun. In diesem Fall verwenden wir, wie eingangs erwähnt, nie mehr als O (K) -Speicher.
Oh ja, ich habe völlig vergessen, dass die
std :: sample- Funktion, die genau das tut, was oben beschrieben wurde, endlich in der Standard-C ++ 17-Bibliothek enthalten ist. Der Standard verpflichtet ihn nicht zur Verwendung von Reservoir-Sampling, sondern zur Arbeit in O (N) -Schritten. Nun, es ist unwahrscheinlich, dass die Entwickler seiner Implementierung in der Standardbibliothek einen Algorithmus wählen, der mehr als O (K) -Speicher verwendet (und auch weniger nicht) - Das Ergebnis muss irgendwo gespeichert werden.
Verwandte Materialien