Hanoi TürmeNur die Faulen haben nicht über das berühmte Spiel von Eduard Luc auf Habré geschrieben. Es scheint, dass alle Abdeckungen abgerissen sind und etwas anderes am Algorithmus nicht mehr hinzugefügt werden kann. Aber nein, dieses Thema hat versteckte Ressourcen. Insbesondere heute werden wir den Algorithmus zum Lösen dieses Puzzles zu einer vollständigen Sortierung wiederholen. (Warum? Nur zum Spaß. Freitag möglich.)
Dieser Beitrag ist der Erinnerung an den wahren Programmierguru Andrei Mrrl Astrelin gewidmet, der mir diesen Algorithmus einmal einfach und verständlich erklärt hat. Der folgende Pseudocode ist der Text seiner Urheberschaft.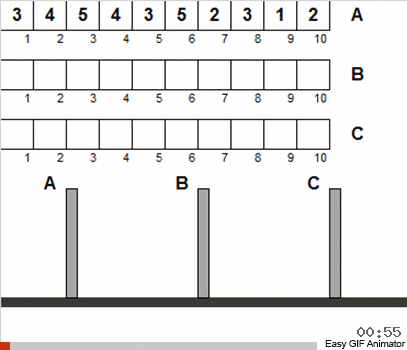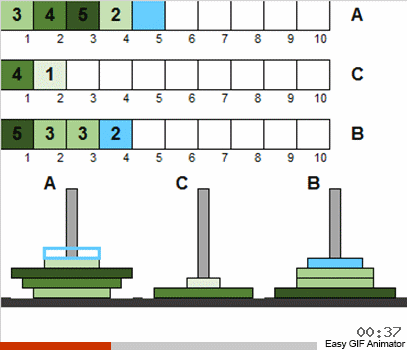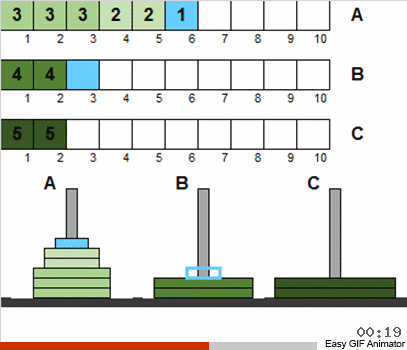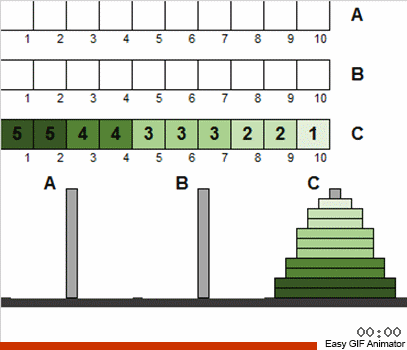
Beim klassischen Puzzle werden zunächst die Scheiben auf der ersten Stange bestellt. Aber wir werden zulassen, dass sie in beliebiger Reihenfolge aufgereiht werden.
Außerdem wird angenommen, dass die Festplattengrößen eindeutig sind. Wir werden uns nicht an diese Einschränkung halten und Wiederholungen zulassen.
Wenn Sie nur diese beiden Freiheiten zulassen, können die Anfangsbedingungen des Puzzles als Array interpretiert werden (Datenträger sind Zahlen), und die Aufgabe besteht darin, dass dieses Array sortiert werden muss.
Die restlichen Bedingungen ändern wir (fast) nicht:
- Wir haben zwei Hilfspole (ein Paar leere Arrays).
- Wir können Discs einzeln übertragen.
- Setzen Sie nur kleinere auf größere (da wir die gleichen Plattengrößen zugelassen haben, können wir die verschobene Platte auch auf andere Platten derselben Größe legen).
- Wir haben das Recht, eine tragbare Festplatte nur mit den obersten Festplatten zu vergleichen (dh alle 3 Arrays sind Stapel).
Unsere Aufgabe: den klassischen rekursiven Puzzle-Algorithmus zu übernehmen ...
def hanoi(n, source, helper, target): if n > 0: hanoi(n - 1, source, target, helper) if source: target.append(source.pop()) hanoi(n - 1, helper, source, target)
... und daraus sortieren!
An der Tatsache, dass wir die anfängliche Störung und Wiederholungen für die Größe der Festplatten zugelassen haben, hat sich daran nichts grundlegend geändert. Im Großen und Ganzen wird das Problem auf dieselbe klassische rekursive Weise gelöst. Das Wichtigste zu verstehen ist, dass alle Scheibenbewegungen in mehrere Stufen unterteilt sind, von denen jede eine klassische Miniatur-Hanoi ist.
Das heißt, wir betrachten in jeder Phase nicht alle verfügbaren Festplatten, sondern nur die Gesamtheit derjenigen, die die alten Bedingungen erfüllen. Nachdem wir dieses kleine Set nach Klassikern sortiert haben, werden wir den allgemeinen Zustand des Systems dem klassischen Puzzle näher bringen. Dann nehmen wir wieder den Satz von Datenträgern, der den Klassikern entspricht, und wenden den bekannten Algorithmus erneut an. Und dieser Satz wird größer sein als im vorherigen Schritt! Und so wiederholen wir, bis sich alle Scheiben an allen Polen plötzlich vom klassischen Zustand unterscheiden.
Das System, gegen das ursprünglich verstoßen wurde (weil die Festplatten nicht am Eingang angeordnet sind), heilt sich bei jeder Iteration selbst aus.
Die Auflösung von Wiederholungen spielt überhaupt keine Rolle. Da die aufeinanderfolgenden identischen Festplatten einfach als eine Festplatte verschoben werden.
Algorithmus
Wir nennen die Spalten
A ,
B ,
C (
A am Anfang ist nicht leer).
Wir stellen die Operationen vor:
A ->
C () - Verschieben Sie eine Platte von
A nach
C.oben (A) ,
oben (C) - die Größe der oberen Scheibe
A oder
C. Wenn die Spalte leer ist, ist diese Größe =
MaxInt .
B ->
C (
K ) - Verschieben Sie alle Platten, deren Größe kleiner als
K ist, von
B nach
C (wir können dies tun, wenn die oberen Scheiben
A und
C nicht kleiner als
K sind ).
swap () - ordne die Spalten
B und
C neu an (oder benenne sie um - es ist uns egal, wo sich die Festplatten befinden).
while (
A ) - Schleife, bis
A leer ist.
Dann funktioniert der folgende Algorithmus:
©
MrrlSchwierigkeit
Im schlimmsten Fall führt die Sortierung zu einer zeitlichen Komplexität des klassischen Algorithmus, der zwar einfach und elegant, aber gleichzeitig maximal ineffizient ist. Was das Beste und Durchschnittliche betrifft, fällt es mir schwer anzunehmen.
Was den Speicher betrifft, können wir sagen, dass bei Verwendung der Rekursion die Kosten entsprechend sind.
Implementierung
Ich habe meine eigene Version nicht in Python geschrieben (ich werde es später tun). Im Abschnitt "Links" unten habe ich jedoch einige Links veröffentlicht, über die Sie Implementierungen in verschiedenen Sprachen sehen können. Besonders interessante Option in Java. Der Autor stützte sich nicht auf die bekannte rekursive Methode zur Lösung des Puzzles, sondern baute den kürzesten Pfadbaum. Vermutlich ist dies die effektivste Lösung, wenn Sie die Sortierung im Stil von "Tower of Hanoi" schreiben.
Algorithmusmerkmale
Referenzen
 Turm von Hanoi
Turm von HanoiImplementierungen:
C ,
Java gegen C ++ gegen Python ,
Python .
Serienartikel:
In der AlgoLab-Anwendung ist diese Sortierung jetzt verfügbar. Obwohl es aufgrund der Extravaganz des Algorithmus zur Klasse der Sortierungen nach Einfügungen gehört, wird es in den Abschnitt "Andere Sortierungen" eingefügt. Es gibt auch eine Einschränkung: Die Zahlen im sortierten Array können nur zwischen 1 und 5 liegen (aufgrund des schwierigen Renderns von Datenträgern). Andere Nummern werden weiterhin durch diese ersetzt.
Die Größe des Arrays ist ebenfalls begrenzt - nicht mehr als 20 Elemente. Dies geschieht ausschließlich in Ihrem eigenen Interesse. Wenn Sie ein zu großes Array verwenden, kann es vorkommen, dass Sie es bis ins hohe Alter sortieren müssen.

Dieser Artikel wurde mit Unterstützung von EDISON Software verfasst, einem Unternehmen, das Smart City Lighting professionell entwickelt und Python-Sites verwaltet.