Theorie des Glücks. Unfälle sind nicht zufällig?

Ich mache die Leser von Habr weiterhin mit den Kapiteln aus seinem Buch "Theory of Happiness" mit dem Untertitel "Mathematical Foundations of the Laws of Meanness" bekannt. Dieses populärwissenschaftliche Buch ist noch nicht veröffentlicht und erzählt sehr informell, wie Mathematik es Ihnen ermöglicht, die Welt und das Leben der Menschen mit einem neuen Grad an Bewusstsein zu betrachten. Es ist für diejenigen, die sich für Wissenschaft interessieren und für diejenigen, die sich für das Leben interessieren. Und da unser Leben komplex und im Großen und Ganzen unvorhersehbar ist, liegt der Schwerpunkt des Buches hauptsächlich auf der Wahrscheinlichkeitstheorie und der mathematischen Statistik. Hier werden Theoreme nicht bewiesen und die Grundlagen der Wissenschaft nicht gegeben, dies ist keineswegs ein Lehrbuch, sondern das, was man Freizeitwissenschaft nennt. Aber genau dieser fast spielerische Ansatz ermöglicht es uns, Intuition zu entwickeln, Vorlesungen für Studenten mit anschaulichen Beispielen aufzuhellen und schließlich Nicht-Mathematikern und unseren Kindern zu erklären, dass wir in unserer trockenen Wissenschaft so interessante Dinge gefunden haben.



In diesem Kapitel diskutieren wir den vorgegebenen Münzflug, topografische Karten, mathematische Katastrophen und die Art der Zufälligkeit. Schauen wir uns dabei Abschnitte der Mathematik an, wie die Theorie der Maßnahmen und die Theorie des dynamischen Chaos.

Das Gespräch über die Gesetze der Gemeinheit als Quelle alltäglicher Turbulenzen beginnt oft mit dem berühmten Gesetz eines Sandwichs . Es ist einfach formuliert, leicht zu überprüfen und weithin bekannt:

Ein Sandwich lässt immer Butter fallen.

Es ist klar, dass das Wort "immer" hier eine Übertreibung ist. Es ist leicht vorstellbar, unter welchen Bedingungen ein Sandwich fallen wird und die geölte Seite intakt bleibt. Was verstehen die Menschen unter diesem Gesetz? Höchstwahrscheinlich fällt das Sandwich oft genug in die Butter, um es wahrzunehmen. Aber ist ein ungünstiges Ergebnis eines Sturzes wahrscheinlicher als ein günstiges? Sandwiches sind unterschiedlich, sie fallen unter verschiedenen Umständen, aus verschiedenen Höhen ... Es gibt so viele Parameter, dass es wahrscheinlich keinen Sinn macht, über Muster in einer solchen Aufgabe zu sprechen. Alles kann passieren. Es kommt vor, dass es in Öl fällt, dann wird es beleidigend, wir erinnern uns an das Gesetz und erinnern uns daran. Und wenn das Sandwich uninteressant wird - wenn das Öl aufgebraucht ist oder sich herausstellt, dass es überhaupt kein Öl enthält, gibt es nichts zu besprechen -, ist klar, dass das Gesetz komisch ist! Am Ende ist ein Sandwich wie eine Münze, mit der Mathematiker Zufallsvariablen mit zwei möglichen Werten erhalten: „Adler“ und „Schwanz“. Wenn die Münze „ehrlich“ ist, spielt es absolut keine Rolle, auf welche Seite sie fallen soll, und wir sagen, dass die Wahrscheinlichkeit, dass der Adler und der Schwanz fallen, gleich und gleich ist $$$1/2$ . Theoretisch sollten Sandwiches gleich sein. Wir werden im nächsten Kapitel darauf zurückkommen, aber jetzt schauen wir uns das wahrscheinlichste einfache Wahrscheinlichkeitssystem an - die Münze.

Eine Münze in wahrscheinlichkeitstheoretischen Experimenten wird auf eine besondere magische Weise geworfen, so dass die Wahl der Anfangsposition, der Anfangsgeschwindigkeit und der Schleudergeschwindigkeit während des Wurfs die Wahrscheinlichkeit eines bestimmten Ergebnisses nicht beeinflusst. Aber es ist offensichtlich, dass dies unmöglich ist! Die Münze ist ein mechanisches System und folgt den Gesetzen der Mechanik, enthält jedoch keine Zufallsvariablen. Die Zukunft in den Bewegungsgesetzen eines so einfachen Körpers wie einer Münze wird eindeutig durch den vergangenen Zustand dieses Körpers bestimmt. Wenn ein Roboter eine Münze wirft oder der Laplace-Dämon ein Fabelwesen ist, das vollständige Informationen über die Koordinaten und Geschwindigkeiten eines mechanischen Systems enthält, werden identische Ergebnisse mit konstanten Anfangsdaten erzielt. Wir sind natürlich keine Roboter oder Dämonen, aber werfen die Leute wirklich Münzen, die so schlampig und unvorhersehbar sind, dass die Gesetze der Mechanik zu Unfällen führen können?

Und woher kommt im Allgemeinen die Zufälligkeit in der Welt, die durch die Gesetze der Mechanik beschrieben wird? Woher kommt der Zufall? Was ist der Unterschied zwischen wirklich chaotischen oder stochastischen Systemen, die grundsätzlich unvorhersehbar sind, und Systemen, in denen es einfach schwierig ist, das Verhalten zu erraten, aber es kann berechnet werden?

Das Münzproblem wurde 1986 von Joseph Keller in Betracht gezogen. Wir liefern eine einfache Erklärung für das Auftreten von Unsicherheit in diesem Prozess, basierend auf den Überlegungen aus Kellers Artikel. Auf welche Seite die Münze fällt, hängt von ihrer Flugzeit ab. $$$t$ und aus der Winkelgeschwindigkeit $$$\ omega$ . Wenn Sie die Winkelgeschwindigkeit in Umdrehungen pro Zeiteinheit messen, wird die Anzahl der Umdrehungen der Münze äußerst einfach ausgedrückt $$$n = t \ omega$ . Diese Abhängigkeit legt die Linien einer gleichen Anzahl von Umdrehungen in den Koordinaten fest $$$(t, \ omega)$ und sie begrenzen wiederum die Bereiche, die einer geraden und ungeraden Anzahl von Umdrehungen entsprechen.

Ein Diagramm, das die Parität der Anzahl der Umdrehungen zeigt, die eine Münze im Flug ausführt. Das Rechteck zeigt den Bereich, in dem die Wahrsagerei auf der Münze am häufigsten stattfindet.

In einem solchen Diagramm ist es möglich zu zeigen, was das Ergebnis eines Münzwurfs sein wird, der um eine bekannte Anzahl von Umdrehungen pro Sekunde verdreht und nach einer bekannten Wurfzeit gefangen wird. Wenn wir in einen weißen Streifen fallen, fällt dieselbe Seite heraus, die beim Werfen oben war, wenn in Orange - das Gegenteil. Linien gleicher Geschwindigkeit sind Hyperbeln, und es ist ersichtlich, dass mit zunehmender Geschwindigkeit der Wechsel von Bereichen immer häufiger wird und die Bereiche selbst dünner werden. Die menschliche Hand ist unvollkommen und eine sehr kleine Streuung der Anfangswerte deckt viele Bereiche gleichzeitig ab, was das Ergebnis unvorhersehbar macht. Im Bereich der Hand (das Rechteck im Diagramm) reicht ein Versatz aus $$$5 \%$ von einem weißen Streifen zu einer Orange springen. Die Frage bleibt: Wie folgt aus dieser Konstruktion die „Ehrlichkeit“ einer echten mechanischen Münze? Wie erhält man die Wahrscheinlichkeit des Verlusts eines Adlers oder von Schwänzen aus dem resultierenden Diagramm?

Ergreifen Sie dringend Maßnahmen!

Wir werden ein wenig in solche Mathematik eintauchen, die nicht in der Schule unterrichtet wird, um besser zu verstehen, worüber wir sprechen. Wir haben in der Einleitung gesagt , dass Mathematiker keine Zahlen oder geometrischen Formen studieren, wie es nach dem Studium eines Schulkurses scheinen mag. Sie arbeiten mit mathematischen Strukturen (abstrakte Algebren, Halbringe, Felder, Monoide, topologische Räume und andere abstrakte Dinge), beschreiben sie, wie es scheint, völlig unverbunden, um zu üben, sie zu definieren, ihre Eigenschaften zu studieren, Theoreme zu beweisen. Und dann verbessern sie ihre Fähigkeiten, solche Strukturen in verschiedenen Wissensbereichen zu finden, und erzielen erstaunlich nützliche Durchbrüche, auch in rein angewandten Bereichen. Wir werden nun ein wenig auf diese Mathematik eingehen und überlegen, wie die Wahrscheinlichkeitstheorie auf der Grundlage eines sehr abstrakten Maßkonzepts aufgebaut ist.

Wir haben die Mechanik der Münze beschrieben und Bereiche erhalten, die Lösungssätze mit bestimmten Eigenschaften beschreiben. Bereiche sind flache Zahlen, wie kann man von ihnen zu Wahrscheinlichkeiten richtig übergehen? Wir müssen unsere Gebiete messen und kommen natürlich zu ihrem Gebiet. Fläche - ist ein Maß für eine flache Figur. Dies ist ein exakter mathematischer Begriff für eine Funktion, die eine Menge mit einem bestimmten nicht negativen numerischen Wert verknüpft. Beispiele für Maßnahmen sind die Mengen in aufgezählten Mengen (z. B. die Anzahl der Äpfel in einem Beutel) sowie die Länge , Fläche und das Volumen der Figuren .

In der Mathematik gibt es einen ganzen Abschnitt, der als Maßtheorien bezeichnet wird . Diese Theorie wurde um die Wende vom 19. zum 20. Jahrhundert geboren (Emil Borel und Henri Lebesgue standen an ihren Ursprüngen) und eröffnete Mathematikern zahlreiche Möglichkeiten zur Analyse sehr komplexer Objekte: Kantor- und Fraktalsätze. Es bildete die Grundlage der Funktionsanalyse und der modernen Wahrscheinlichkeitstheorie, deren Grundstein der bemerkenswerte russische Mathematiker Andrei Kolmogorov legte. Die Definition der Wahrscheinlichkeit als Maß ermöglicht es Ihnen, alle grundlegenden Eigenschaften der Wahrscheinlichkeit sowohl für diskrete als auch für kontinuierliche Mengen anzuzeigen.

Obwohl unser Buch kein Lehrbuch ist, lohnt es sich, ein wenig anzuhalten, um die Konzepte der Wahrscheinlichkeit von Thorium aus der Vogelperspektive zu betrachten und den Geschmack der Mathematik zu spüren. Zunächst listen wir die Haupteigenschaften aller Maßnahmen auf. Um sie sich besser vorstellen zu können, können Sie anstelle des Wortes "Maß" die Wörter "Menge" oder "Länge" oder "Fläche" verwenden.

1. Das Maß der leeren Menge ist Null.
2. Das Maß der gesamten messbaren Menge ist endlich für endliche Maße.
3. Das Maß der Teilmenge überschreitet nicht das Maß der Menge
4. Das Maß der Vereinigung zweier beliebiger Mengen ist gleich der Summe der Maße dieser Mengen abzüglich des Maßes ihrer Schnittmenge (Additivität).
5. Das Maß für die Ergänzung einer Teilmenge entspricht der Differenz zwischen den Maßen der gesamten Menge und dem Maß für die Teilmenge.

Kann eine nicht negative numerische Funktion ein Maß sein? Überhaupt nicht. Zum Beispiel gibt das Alter einer Person eine ganz bestimmte Nummer. Das Alter von zwei Personen kann jedoch nicht als Summe ihres Alters definiert werden. Und Laufgeschwindigkeit ist kein Maß - zwei Personen laufen nicht doppelt so schnell. Aber Impuls (Impuls) oder Energie hat bereits die Eigenschaften eines Maßes. Das Gewicht, die Menge an Geld, die Menge an Wissen, das Volumen des Schreiens, obwohl nicht immer leicht messbare Dinge, können auch für viele Menschen als Maß dienen.

Auf einer intuitiven Ebene ist heute fast jeder mit dem Konzept der Wahrscheinlichkeit vertraut. Es wird von Politikwissenschaftlern und Journalisten in Talkshows geschätzt, es wird über die globale Erwärmung oder den Regen von morgen gesprochen, Witze darüber werden erzählt: Wie hoch ist die Wahrscheinlichkeit, einen Dinosaurier auf dem Tver zu treffen? - Eine Sekunde: entweder ein Treffen oder nicht. In der modernen Mathematik wird das Konzept der Wahrscheinlichkeit als Maß für eine spezielle Menge definiert, die als Wahrscheinlichkeitsraum bezeichnet wird . Es enthält sowohl Elementarereignisse als auch deren Kombinationen, die unter Verwendung der Operationen Vereinigung, Schnittmenge und Ausschluss erhalten werden. Ein Beispiel für ein elementares Ereignis: "Verlust eines Triple beim Werfen eines Knochens." Ein Beispiel für ein Ereignis, das nicht elementar ist: "Der Verlust einer geraden Zahl außer zwei." Also listen wir die Eigenschaften der Wahrscheinlichkeit auf:

1. Die Wahrscheinlichkeit eines unmöglichen Ereignisses ist Null.
2. Die Wahrscheinlichkeit für den gesamten Wahrscheinlichkeitsraum ist gleich Eins.
3. Wenn ein Ereignis auch ein anderes mit sich bringt, überschreitet die Wahrscheinlichkeit des zweiten nicht die Wahrscheinlichkeit des ersten. Hier entspricht die Beziehung "beinhaltet" für Ereignisse "ist eine Teilmenge" für Mengen und bedeutet nicht "ist eine Ursache".
4. Die Wahrscheinlichkeit des Auftretens mindestens eines von zwei beliebigen Ereignissen ist gleich der Summe der Wahrscheinlichkeiten jedes dieser Ereignisse abzüglich der Wahrscheinlichkeit, dass die Ereignisse gleichzeitig eintreten.
5. Die Wahrscheinlichkeit, dass ein Ereignis nicht eintritt, ist eins minus der Wahrscheinlichkeit, dass ein Ereignis eintritt.

Wenn Sie sich die Eigenschaften von Kennzahlen und Wahrscheinlichkeiten genauer ansehen, werden Sie feststellen, dass es sich um dieselben Eigenschaften handelt.

Nicht alle Eigenschaften der Wahrscheinlichkeit ergeben sich aus ihrer Definition als Maß: Die Konzepte der Unabhängigkeit von Ereignissen und die Methode zur gleichzeitigen Berechnung der Wahrscheinlichkeit von zwei oder mehr unabhängigen Ereignissen als Produkte aus Wahrscheinlichkeiten werden durch bedingte Wahrscheinlichkeit eingeführt , aber diese Konzepte stimmen mit der Kolmogorov-Definition überein.

Diskrete Zufallsvariablen entsprechen endlichen zählbaren Mengen, in denen ein natürliches Maß eine gewöhnliche Zählung der Anzahl von Elementen ist. Dementsprechend ist die Wahrscheinlichkeit in einem diskreten Wahrscheinlichkeitsraum die kombinatorische Berechnung von Optionen, die jedem Schüler bekannt ist. Bei kontinuierlichen Zufallsvariablen entspricht die Wahrscheinlichkeit als Maß eher der Länge oder Fläche, und hier geht es um Wahrscheinlichkeitsdichten .

Die Wahrscheinlichkeitsanalogie mit dem Maß endet hier nicht. Was ist der Durchschnittswert ? Dies ist ein Analogon zur Position des Massenschwerpunkts einer Figur, die aus Punktmassen oder einem Festkörper mit bekannter Dichte besteht. Und diese Größen werden auf die gleiche Weise berechnet. Und wie ist die Streuung von Zufallsvariablen um den Durchschnitt charakterisiert: Varianz ? Genau wie das Trägheitsmoment die Massenverteilung um den Massenschwerpunkt kennzeichnet. Und wieder stimmen die Formeln zur Berechnung der Varianz für eine Probe oder Verteilung mit den Formeln für das Trägheitsmoment eines Satzes von Körpern oder eines festen Körpers von gerissener Form überein.

Übrigens, wenn wir in den Definitionen und Eigenschaften der Wahrscheinlichkeit die Summe durch „Maximum“ und das Produkt durch „Minimum“ ersetzen, können wir eine alternative Theorie konstruieren, die als Theorie der Möglichkeiten bezeichnet wird . So funktioniert Mathe. Wir beginnen mit abstraktem Denken: Zahlen bilden eine Algebra mit Additions- und Multiplikationsoperationen, aber in einem begrenzten Zahlenintervall können Sie eine ähnliche Algebra mit Minimal- und Maximaloperationen erstellen. Wir bauen das Maßkonzept auf einer neuen Algebra auf und stellen fest, dass es eine neue Sicht auf die Welt eröffnet! Im Gegensatz zur Wahrscheinlichkeitstheorie können in einer solchen Theorie zwei koordinierte Maße konstruiert werden - die Möglichkeit und die Notwendigkeit , und im Gegensatz zur Wahrscheinlichkeit stimmen sie gut mit den Operationen des Kombinierens und Überschneidens von Ereignissen überein. Diese Richtung wurde vom Amerikaner Lotfi Zadeh, einem Aserbaidschaner, geschaffen. Sie dient als Grundlage für Fuzzy-Logik und wird in automatischen Mustererkennungs- und Entscheidungsfindungssystemen verwendet.

Unglaublich, aber wahr!

Die erste Eigenschaft von Maßnahmen scheint trivial, ist aber in ihrer Asymmetrie interessant. Wenn das Maß der Teilmenge Null ist, bedeutet dies nicht, dass sie leer ist! Eine Linie ist beispielsweise eine Teilmenge der Punkte in einer Ebene, ihre Fläche (Maß) ist jedoch Null. Es gibt exotischere Beispiele - Cantor- und Fraktalsätze mit einer komplexen Struktur, die eine unendliche Anzahl von Punkten enthält, die einen bestimmten Bereich oder ein bestimmtes Volumen visuell „einnehmen“, aber dennoch kein Maß haben.

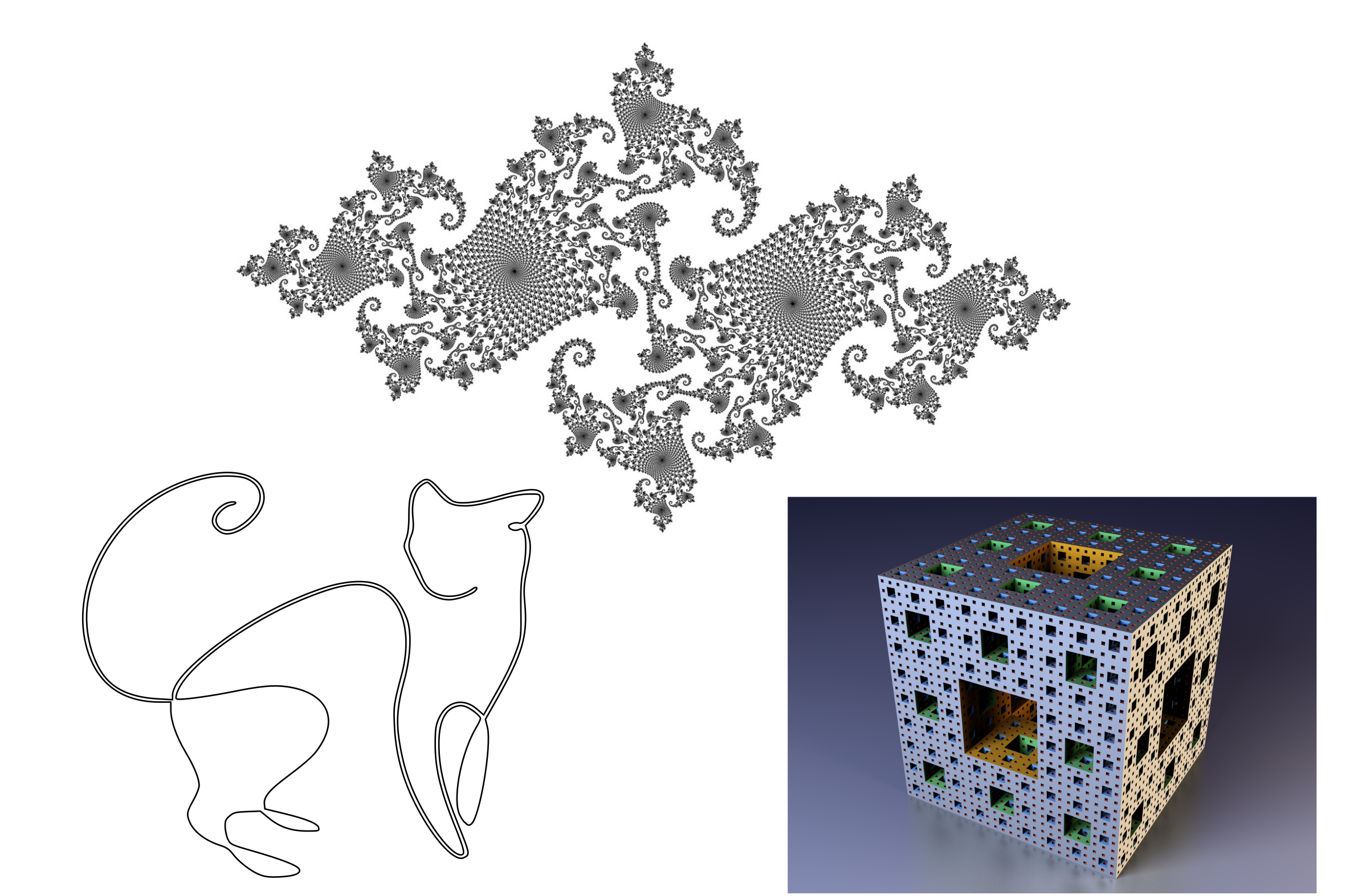Einige Objekte von Null messen: eine Linie in einer Ebene, sporadisches Julia-Set, Menger-Fraktalschwamm.

Während ich diese Illustration vorbereitete, fand ich ein wundervolles Bild einer nicht verbundenen Gruppe von Julia auf einem transparenten Hintergrund mit hoher Auflösung. Nachdem ich es in den Vektoreditor eingefügt hatte, stieß ich auf eine lustige Schwierigkeit - es war sehr schwierig, mit der Maus in dieses Bild zu gelangen, um es auszuwählen. Es ist so „locker“, dass die Wahrscheinlichkeit, in ein gefülltes Pixel zu gelangen, merklich geringer war als in einen transparenten Hintergrund. Im Wahrscheinlichkeitsraum können auch Teilmengen mit dem Maß Null existieren, dies bedeutet jedoch nicht, dass Ereignisse aus diesen Teilmengen unmöglich sind. Vom vierten bis zum fünften Versuch konnte ich immer noch das Bild auswählen, da die Pixel eine endliche Größe haben. Aber was würde passieren, wenn ich eine wirklich inkohärente Gruppe von Julia mit unendlicher Auflösung zur Verfügung hätte?

Stellen Sie sich vor, Sie verwenden einen Software-Zufallszahlengenerator, aus dem eine beliebige reelle Zahl erzeugt wird $$$0$ vorher $$$1$ . Wie groß ist die Wahrscheinlichkeit, dass eine Zahl herausfällt? $$$0$ ? und Zahlen $$$1/2$ oder $$$e / \ pi$ ? In all diesen Fällen lautet die Antwort - Null! Vielmehr die kleinste positive Zahl, die dem Computer zur Verfügung steht, das sogenannte Maschinen-Epsilon, da der Computer mit einer endlichen Anzahl von Dezimalstellen arbeitet. Warten Sie, sagen Sie, in welchem ​​Sinne ist Null? Die gleichen Zahlen sind nicht unmöglich. Lassen Sie uns ein Experiment durchführen, als Ergebnis erhalten wir eine bestimmte Zahl, und wenn wir sie erhalten, kann die Wahrscheinlichkeit ihres Auftretens „konstruktionsbedingt“ nicht Null sein. Das stimmt, aber wie lange sollte ich warten, bis genau 0 ausfällt? Fast endlos! Tatsache ist, dass eine einzelne Zahl wie ein Punkt auf einem Segment ein Nullmaß und eine ehrliche Nullwahrscheinlichkeit hat. Nur ein Maß für ein kontinuierliches Segment, auch ein sehr kleines, ist ungleich Null. Wir sprechen also nicht von Wahrscheinlichkeit, sondern von Wahrscheinlichkeitsdichte, die, multipliziert mit einem endlichen Maß einer Teilmenge in einem Wahrscheinlichkeitsraum, einen endlichen Wert ergibt - die Wahrscheinlichkeit, in diese Teilmenge zu fallen. Übrigens, stellen Sie sich als unser idealer Zufallszahlengenerator mit unendlicher Genauigkeit heraus. Die Wahrscheinlichkeit, eine rationale Zahl (keine konkrete, aber eine) damit zu erhalten, ist ebenfalls Null. Der Beweis, dass rationale Zahlen eine dichte Teilmenge des Nullmaßes der Menge der reellen Zahlen bilden, machte Ende des 19. Jahrhunderts Lärm.

Wenn jemand geduldig tausend Experimente mit einer Münze durchführt und Ihnen glücklich sagt, dass er so viele „Adler“ wie „Schwänze“ hat, können Sie sicher Zweifel äußern oder ihm zu seltenem Glück gratulieren. Obwohl das Werfen einer Münze und eines diskreten Zufallsprozesses mit zunehmender Statistik zunimmt, nimmt die Leistung des Wahrscheinlichkeitsraums zu und das Maß des Ereignisses: „Die Anzahl der„ Adler “stimmt mit der Anzahl der„ Schwänze “überein. Mit der Stirling-Formel kann gezeigt werden, dass die Wahrscheinlichkeit dieses „wahrscheinlichsten“ Ereignisses mit zunehmender Anzahl von Tests als gegen Null geht $$$1 / \ sqrt {\ pi n}$ . Für hundert Abgüsse sind dies etwas mehr als fünf Prozent, für zehntausend - nur ein halbes Prozent. In solchen Fällen sagen Mathematiker: Mit ziemlicher Sicherheit wird die Anzahl der „Adler“ nicht der Anzahl der „Schwänze“ entsprechen . Egal wie seltsam es klingt, aber „mit ziemlicher Sicherheit“ ist ein exakter mathematischer Begriff, was bedeutet, dass das Ereignis eine Ergänzung zu einer Teilmenge des Wahrscheinlichkeitsraums des Nullmaßes ist. Wir werden in einem der folgenden Kapitel auf diese Überlegungen zurückkommen, wenn wir uns fragen: Wie viel jeder von uns für normal halten kann.

Überprüfung der Ehrlichkeit einer echten Münze

Kehren wir zur Münze und ihrer Ehrlichkeit zurück. Die Kolmogorov-Definition der Wahrscheinlichkeit hat ihre Frequenzdefinition (als relative Häufigkeit auftretender Ereignisse) und ihre geometrische Definition (als Bruchteil des "Volumens" eines Ereignisses im gesamten "Volumen" der Möglichkeiten) in Einklang gebracht. Der Anteil der Fläche der weißen Streifen im Diagramm, der für eine rotierende Münze berechnet wurde, spiegelt somit die Wahrscheinlichkeit wider, von derselben Seite zu fallen, auf die wir sie geworfen haben.

Aber das Problem! Die Fläche jedes Streifens in unserem Diagramm ist unendlich (wenn wir das gesamte Viertel der Koordinatenebene betrachten). Die Additivität der Maßnahme ermöglicht es uns jedoch, genau zu zeigen, dass dies nicht verhindert, dass die Bereiche der schattierten und weißen Bereiche gleich sind. In expliziter Form haben die Gleichungen für unsere Kurven die Form$$$\omega = n/t$ . Ist der Bereich unter der Kurve $$ω = 1 / t ist gleich$\omega = 1/t$$$S , dann aufgrund der Additivitätseigenschaft die Fläche unter der Kurve$S$$$ω = n / t ist gleich$\omega = n/t$$$$S_n = n S$ . Für einzelne Streifen erhalten wir wiederum: $$$S_{n} - S_{n-1} = n S - (n-1)S = S$ .Es stellt sich heraus, dass der Flächenunterschied nicht von der "Anzahl" der Hyperbel abhängt. Dies ist nichts Besonderes in Bezug auf Hyperbeln, die gleiche Schlussfolgerung kann für jede Kurve der Form gezogen werden$$y = n f ( x ) , wenn nur die Funktion$y = n f(x)$$$f war messbar. Und wenn ja, dann ist es für den gesamten Definitionsbereich ebenso wahrscheinlich, in den weißen Teil des Diagramms oder in den schattierten zu gelangen, wie es für eine „ehrliche“ Münze erwartet wird. Die Argumentation, die wir gerade gegeben haben, scheint einfach zu sein, aber sie liefert ein sehr allgemeines Ergebnis, das auf alle additiven Mengen anwendbar ist. Das abstrakte Maßkonzept ermöglichte es uns, endlose Größen untereinander zu vergleichen und dabei im Rahmen von Logik und gesundem Menschenverstand zu bleiben. Abstraktion ist gut, aber es kann argumentiert werden, dass wir in Wirklichkeit nicht Münzen mit allen möglichen Parametern werfen. Wie Experimente mit einer Hochgeschwindigkeitskamera zeigten, fallen die Winkelgeschwindigkeiten in den Bereich von$f$



$$$20$ vorher $$40 Umdrehungen pro Sekunde und die Flugdauer beträgt eine halbe bis eine Sekunde. Dieser Bereich wird im Diagramm durch ein Rechteck hervorgehoben. Darin ist die Gesamtfläche der weißen Streifen etwas größer als die der orangefarbenen, und wir können daraus schließen, dass die Wahrscheinlichkeit, von derselben Seite zu fallen, die während des Werfens war, groß ist$40$$$$50.6\%$ .

2007 veröffentlichte eine Gruppe von Percy Deaconess et al. Aus Stanford einen Artikel , der eine detaillierte Analyse des Prozesses des Münzwurfs enthält. Eine detaillierte Beschreibung der Mechanik einer fliegenden und rotierenden Scheibe, die sich nicht nur dreht, sondern auch bewegt - die Rotationsachse selbst dreht sich im Flug - zeigt, dass bei einem manuellen Wurf aus der Position „Adler von oben“ die Wahrscheinlichkeit, dass der „Adler“ um ein Hundertstel fällt, mehr als die Hälfte beträgt.

Ist es viel oder wenig? Wie viele Experimente benötigen Sie, um einen solchen Unterschied zu machen? Wenn sich experimentelle Daten ansammeln, nimmt der Standardfehler des Mittelwerts, der den Fehler widerspiegelt, mit dem der Mittelwert berechnet werden kann, proportional zur Quadratwurzel der Anzahl der Tests ab:$$σ μ = σ / √n hier$\sigma_{\mu} = \sigma/\sqrt{n}$$$σ ist die Standardabweichung für die untersuchte Verteilung. In unserem Fall für die Bernoulli-Verteilung mit Wahrscheinlichkeit$\sigma$$$0,51, was gleich ist$0.51$$$$\sqrt{0.51\times0,49}\approx0.5$ . Um die Abweichung des Durchschnitts von einem Hundertstel sicher zu identifizieren, sollte diese Abweichung überschritten werden $$3 Standardabweichungen. Somit können wir die Anzahl der Versuche abschätzen:$3$

$$

$$n = \left(\frac{\sigma}{\sigma_{\mu}}\right)^2 = \left(\frac{3\times0.5}{0.01}\right)^2 \approx 22500$$

So oft müssen Sie eine Münze werfen, um die mechanistische Vorbestimmung des Ergebnisses zu bemerken. Um klarer zu machen, was gemeint ist, werde ich ein Beispiel von zweihundert Tests idealer und leicht unvollkommener "Münzen" geben, die durchgeführt wurden, um die Wahrscheinlichkeit des Verlusts beispielsweise eines Adlers zu berechnen. Jeder Test besteht aus$$40.000 Würfe. Die Wörter "Münze" und "Werfen" stehen in Anführungszeichen, da tatsächlich keine physische Münze verwendet wurde, sondern ein Zufallszahlengenerator, der der Bernoulli-Verteilung gehorcht.$40000$

Experimente mit dem Werfen einer idealen und leicht unvollkommenen Münze, um die Unvollkommenheit zu beheben.

Es ist zu sehen, dass erst nach$$20.000 Tests der „Wolke“ der beobachteten Mittelwerte beginnen sich deutlich zu trennen. Nun, für den häuslichen Gebrauch können wir davon ausgehen, dass die Münze ein guter Generator für eine zufällige Auswahl von zwei gleich wahrscheinlichen Optionen ist.$20000$

Tourismusrecht

Die Äquivalenz der geometrischen und Frequenzbestimmung der Wahrscheinlichkeit enthüllt das Geheimnis eines Gesetzes der Gemeinheit, das Touristen, Geologen und allen, die topografische Karten verwenden, bekannt ist:

Der Ort, an den der Tourist geht, befindet sich meistens entweder auf der Falte der Karte oder am Rand des Blattes.

Angenommen, wir interessieren uns gleich häufig für Objekte in allen Teilen der Karte. Wir sind jedoch selten an Objekten mit Nullmaß interessiert - der springende Punkt bei der Verwendung einer Karte ist die Vermessung der Umgebung des Objekts, dh eines endlichen Bereichs. Lass uns einen kleinen Bruchteil reichen$$α aus dem Bereich der gesamten Karte$\alpha$$$S, um herauszufinden, wie man zum Objekt kommt. Wenn sich das Objekt in einem kritischen Abstand einer Biegung oder Kante nähert$S$$$d , wir werden das Tourismusgesetz als erfüllt betrachten. Der Anteil der Grenzgebiete an der Gesamtfläche der Karte gibt uns die Möglichkeit, dieses Gesetz der Gemeinheit an uns selbst zu erfahren. So sehen die unangenehmen Teile der Karte aus, wenn$d$$$α = 0,5 % und in einer Biegung.$\alpha=0.5\%$

Grau zeigt "schlechte" Bereiche an. Ein Diagramm mit einer Fläche von einem halben Prozent für eine 40 cm breite Karte wird separat angezeigt. Der Durchmesser beträgt etwas mehr als 3 cm.

Für eine quadratische Karte$$$d = \sqrt{\alpha S}$ . Unangenehme Streifen haben eine Fläche $$$d \sqrt{S} = S\sqrt{\alpha}$ .Vier Streifen, zwei vertikale und zwei horizontale, befinden sich am Rand. Jede zusätzliche horizontale oder vertikale Biegung fügt einen weiteren Streifen hinzu. Gleichzeitig fügen sich kreuzende Streifen zusätzliche Quadrate mit einer Fläche hinzu$$$d^2 = \alpha S$ . Durch Falten der Karte, so dass es sich herausstellt $$$n$ horizontal und $$$m$ Bei vertikalen Biegungen ergibt sich eine Gesamtfläche der unangenehmen Zone von: $$$S (n + 2) \ sqrt {\ alpha} + S (m + 2) \ sqrt {\ alpha} -S (n + 2) (m + 2) \ alpha$ . Wenn wir es in den Bereich der gesamten Karte bringen, erhalten wir einen unangenehmen Anteil an der Gesamtfläche:

$$

$$p = (n + m + 4) \ sqrt {\ alpha} - (n + 2) (m + 2) \ alpha.$$

Die Abbildung zeigt die Bereiche, in denen dieser Anteil übersteigt $$$50 \%$ für verschiedene Werte $$$\ alpha$ .

Bereiche, in denen die Wahrscheinlichkeit erhöht ist, dass sie sich am Rand der Karte oder am Rand befinden. Zahlen geben den Bruchteil der Fläche der betrachteten Nachbarschaft von der Fläche der gesamten Karte an.

Es stellt sich heraus, dass eine zweimal gefaltete Karte in Bezug auf einen Touristen bereits formal als unehrlich angesehen werden kann. Meistens haben Karten drei vertikale und drei horizontale Falten, was die Wahrscheinlichkeit ergibt, das Gemeinheitsgesetz mit einer Wahrscheinlichkeit von ungefähr zu erfüllen $$$60 \%$ bei $$$\ alpha = 0,5 \%$

Woher kommt der Zufall?

In Souvenirläden finden Sie Magnetpendel für "Wahl der Wünsche". Auch sie sind mechanische Zufallsgeneratoren und werden manchmal fälschlicherweise als „chaotische Pendel“ bezeichnet. Das Pendel startet die Bewegung von einer Ausgangsposition und Geschwindigkeit aus, führt eine Reihe von „unvorhersehbaren“ Schwingungen aus und stoppt schließlich in einem der Sektoren. Die Schwankungen sind hier jedoch nicht unvorhersehbar, sie sind einfach sehr empfindlich gegenüber den Anfangsbedingungen. Für jeden Sektor, in dem das Pendel anhalten kann, gibt es einen Anziehungsbereich im Koordinatengeschwindigkeitsraum. Dies ist eine Reihe solcher Anfangsbedingungen, unter denen das Pendel notwendigerweise bis zu einem bestimmten Punkt im angegebenen Sektor anzieht. Der Haltepunkt des Pendels wird als Attraktor bezeichnet - als Anziehungspunkt. Bei einem Pendel aus dem Bild ist der Raum der Koordinaten und Geschwindigkeiten vierdimensional, so dass es nicht einfach ist, den Anziehungsbereich darzustellen. Wenn wir uns jedoch auf nur zwei Sektoren beschränken und das Problem auf eindimensional reduzieren (ein solches Pendel wird als Duffing-Oszillator bezeichnet), wird der Raum der Anfangswerte zu einer Ebene, sodass die Anziehungsbereiche sichtbar werden. Sie sehen aus wie ein kompliziertes Yin-Yang-Symbol und verwandeln sich schnell in schmale Streifen, die die Anziehungsbereiche trennen.

Anziehungspunkte von Attraktoren für ein eindimensionales Pendel von Wünschen - der Duffing-Oszillator.

Wie bei der Münze, bei der sich die Anfangsbedingungen leicht verschieben, gelangen wir von einem Attraktor zum anderen. Würfel und Roulette funktionieren auf die gleiche Weise, aber sie sind selbst keine zufälligen Generatoren. Dies sind keine wirklich chaotischen Systeme und ihr Verhalten kann genau berechnet werden.

Aber was ist ein echter Zufall? Ein gutes Beispiel für ein echtes stochastisches System ist das Auftreten von Autos auf der Straße. Die Leute sind sich nicht einig, koordinieren ihre Pläne nicht, jedes Element des Ensembles außerhalb der Straße handelt unabhängig. Und obwohl das Verhalten der Menschen bestimmte Verhaltensmuster aufweist - Hauptverkehrszeiten morgens und abends, leere Straßen nachts usw., haben und werden wir nicht genug Informationen über jeden Teilnehmer der Bewegung haben, um das Auftreten eines von ihnen vorherzusagen. Die Mechanik von Elementarteilchen auf Quantenebene, der Zerfall instabiler Atome, Änderungen des genetischen Codes, höchstwahrscheinlich Erdbeben und Börsenkurse an der Börse sind ebenfalls stochastisch. Für den Forscher bleibt nur noch, sie als Zufallsvariablen zu betrachten und mit der Wahrscheinlichkeitstheorie zu beschreiben.

Aber es gibt noch eine andere Zufallsquelle - dynamisches Chaos . Chaotische Systeme unterscheiden sich von stochastischen darin, dass sie durch exakte Gleichungen und Parameter beschrieben werden, die keine Zufälligkeit enthalten. Ihr Verhalten ist jedoch nicht nur kompliziert, sondern auch chaotisch und wirklich unvorhersehbar. Wenn wir beginnen, das Pendel der Wünsche sehr sorgfältig mit genau gesteuerter Frequenz und Amplitude zu schwingen, werden wir feststellen, dass seine gleichmäßigen Bewegungen für eine lange Zeit nicht berechnet werden können. Keine Algorithmen auf willkürlich genauen Computern erlauben es uns, das genaue Verhalten des Pendels für eine willkürlich entfernte Zukunft zu berechnen. Er wird in keinem Sektor anhalten, sondern sanfte Bewegungen ausführen, aber niemals zweimal zum selben Punkt im Koordinatengeschwindigkeitsraum zurückkehren. Ein weiteres Beispiel für ein extrem einfaches chaotisches System ist ein idealer Ball, der im Schwerefeld auf einem idealen Tisch mit Feder springt. Die relativ einfachen Lorentz-Gleichungen haben gezeigt, dass wir das Wetter nie länger als ein paar Wochen vorhersagen können - dies ist auch ein chaotisches System.

Die Theorie des dynamischen Chaos konnte die Natur einer solchen Unvorhersehbarkeit erklären. Das einfache eindimensionale Pendel der Wünsche, das wir untersucht haben, hatte zwei stabile stationäre Punkte - zwei Attraktoren und einen instabilen, von dem das System zu entkommen versucht. Dies wird durch einen weißen Kreis dargestellt. Im chaotischen Modus erscheint anstelle einer Reihe von Attraktoren eine unendliche Anzahl instabiler stationärer Trajektorien im System. Diese Menge ist unendlich, hat aber ein Nullmaß und ist eine sehr komplizierte disjunkte Struktur. Einmal auf einer dieser Trajektorien, ist es im Prinzip unmöglich, sie mit endlichen Algorithmen zu verfolgen. Am überraschendsten war jedoch, dass diese unendliche Anzahl instabiler Flugbahnen an sich attraktiv ist! 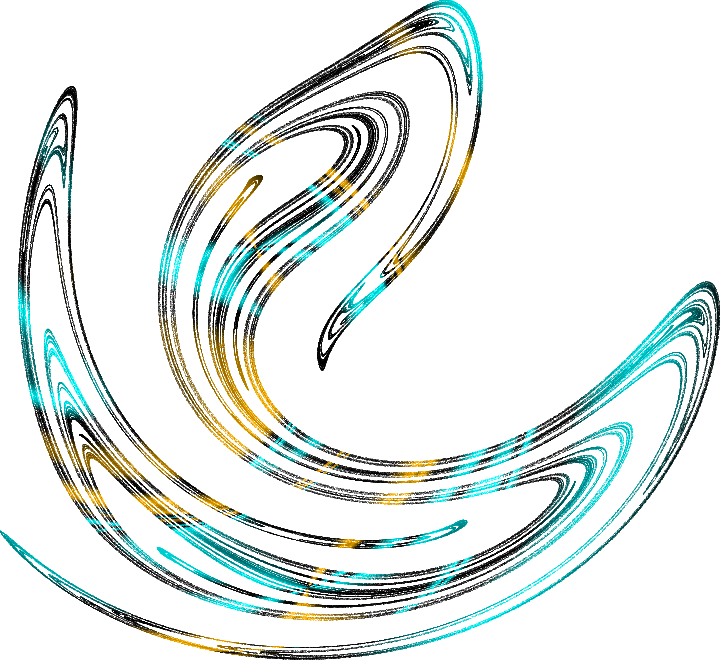Das chaotische System springt kontinuierlich von der Nähe einer instabilen Flugbahn zur nächsten und bleibt dabei innerhalb der Grenzen dieses seltsamen Attraktors. Diese Sets heißen also: seltsame Attraktoren . So sieht der Abschnitt eines seltsamen Attraktors für ein Pendel von Wünschen, der harmonischen Schwingungen ausgesetzt ist, faszinierend schön aus. Dieses Objekt für ein eindimensionales Pendel kann im dreidimensionalen Raum (Koordinate, Geschwindigkeit, Phase der erzwungenen Schwingung) beschrieben werden. Wenn Sie einen Attraktor in diesem Raum durch eine Ebene schneiden, können Sie seine Struktur sehen, dies wird als Poincare-Abschnitt bezeichnet . Jeder Punkt hier ist eine Spur der Flugbahn, und die Farbe der Punkte spiegelt die relative Geschwindigkeit wider, mit der die Flugbahnen voneinander streuen. Hier sind ein paar schöne seltsame Attraktoren:


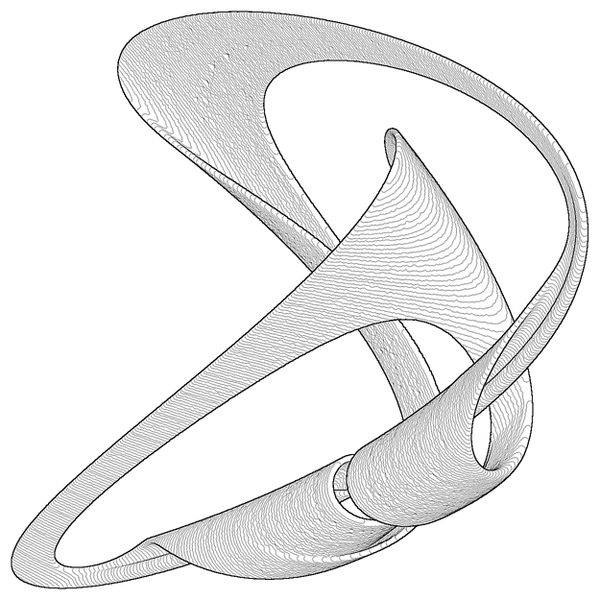Links: Poincare-Abschnitt für die Flugbahn eines Balls, der auf einem federbelasteten Tisch springt. Viele Punkte gehören zur Oberfläche der Kugel, die dem Gesetz der Energieerhaltung entspricht. Rechts: Ein Volumenbereich, der einen seltsamen Attraktor umschließt, der bei erzwungenen Vibrationen einer dicken Platte entsteht.

Die Glätte der chaotischen Flugbahn ermöglicht es Ihnen, ein wenig in die Zukunft zu schauen. Dies erklärt eine ärgerliche Beobachtung: Einerseits können Wettervorhersager das Wetter manchmal nicht sicher für eine Woche vorhersagen, andererseits, wenn Sie sagen, dass morgen das gleiche Wetter wie heute sein wird, werden Sie sich in etwa drei von vier Fällen nicht irren . Im Allgemeinen sind Witze über Wettervorhersagen unfair und wir müssen dem menschlichen Denken und der Beharrlichkeit Tribut zollen, die es ermöglicht haben, das Wetter auf einem modernen Niveau vorherzusagen!

Dynamisches Chaos ist theoretisch sehr komplex und schön, es entstehen Bilder von erstaunlicher Eleganz, aber es kann auch nützlich sein. Beispielsweise sind auch die Algorithmen, mit denen Zufallszahlen in Computern erzeugt werden, deterministisch. Für die Beispiele in diesem Buch habe ich einen Pseudozufallszahlengenerator verwendet, der den eigentlichen stochastischen Prozess (Alpha-Zerfall oder Zählen von Autos auf der Straße) nicht gestartet hat, sondern die nächste "Zufallszahl" basierend auf den vorherigen berechnet hat, die er zuvor erhalten hat.

Von Münzen über Schmetterlinge bis hin zum Schicksal

Beobachtungen, wie kleine Abweichungen zu globalen Veränderungen im System führen, führen zum Gedanken an den „Schmetterlingseffekt“. Ich möchte Sie daran erinnern, dass dieser Effekt eine Kette weitreichender dramatischer Konsequenzen eines auf den ersten Blick unbedeutenden Ereignisses bedeutet. Der Schmetterling in Ray Bradburys Kurzgeschichte "And the Thunder schlug ein" wurde von Forschern der Vergangenheit zerquetscht und führte zu einer radikalen Umstrukturierung der Zukunft. Und einer seiner Vorträge, Edward Lorenz, Schöpfer der Theorie des dynamischen Chaos, mit dem Titel: "Kann ein Flügelschlag eines Schmetterlings in Brasilien einen Tornado in Texas verursachen?"

Wir beziehen uns implizit auf diesen Effekt und beklagen: "Wenn ich nicht um die Ecke gegangen wäre, wäre alles anders gewesen!", "Wenn er nicht in diesen Zug gestiegen wäre, hätte es keine Katastrophe gegeben!" oder "Wegen solcher Kleinigkeiten haben sie sich gestritten und getrennt !!" Wir sehen jedoch, dass eine wahrhaft stochastische Quantenwelt und ultrapräzise Atomuhren in der Welt nebeneinander existieren, stabile Hamilton-Systeme in der Welt der Sterne und Galaxien und das Chaos der Saturn- oder Kuiperringe, die thermische Bewegung von Molekülen und die erstaunliche Genauigkeit des Betriebs biologischer Systeme oder Automobilmechanismen. Nein, die Flügelklappe eines Schmetterlings verursacht keine Hurrikane, sondern verschwindet spurlos und führt zu einer Kette von Wirbeln, die Energie und Informationen an immer kleinere Wirbel übertragen, bis sowohl Energie als auch Informationen im Chaos der Schwankungen verschwinden. Es sollte klar sein, dass kleine Abweichungen nur dann zu einer grundlegenden Reorganisation des Systems führen, wenn es instabil ist oder kurz vor einer Gabelung oder Katastrophe steht - so wird die globale Umstrukturierung des Verhaltens des Systems mit kleinen Änderungen der Parameter in der Sprache der Mathematik bezeichnet. Und Gabelungen bilden im Parameterraum immer Mengen von Nullmaßen - das sind Punkte oder Grenzen. Kleine Störungen führen nicht fast überall zu Katastrophen (dies ist auch ein genauer Begriff, der „überall, mit Ausnahme eines Satzes von Null“ bedeutet), und instabile Zustände in der Natur werden selten beobachtet, ohne den „Test der Zeit“ zu bestehen.

Wenn sich das Paar „wegen Unsinns“ trennte, war sie auf jeden Fall dazu bestimmt, sich zu trennen, sie war instabil. Stabile Paare durchleben Kriege und Hungersnöte und lösen sich manchmal auf, aber nicht aufgrund von Kleinigkeiten, sondern aufgrund tiefgreifender Veränderungen, die einem Menschen während seines Lebens passieren können. In der Kette von Ereignissen, die zum Zugunglück geführt haben, ist es nicht einfach, ein Schlüsselereignis (einen bestimmten Fehler oder einen tödlichen Unfall) herauszufinden, und höchstwahrscheinlich ist der Schlüssel kein Ereignis, sondern ein systematischer Verstoß gegen die Regeln, der das System in einen instabilen Zustand führt. Wenn das System viele Parameter enthält und einige davon zufällig sind und unser Leben so strukturiert ist, gehen die Informationen in einem solchen System verloren, und es ist nicht möglich, genau zu dem Zeitpunkt in unserem Leben wiederherzustellen, an dem „alles schief gelaufen ist“. Quälen Sie sich nicht mit Bedauern darüber, was passiert ist, sondern schauen Sie sich genauer an, was jetzt mit Ihnen passiert, um den eigentlichen Punkt der Gabelung nicht zu verpassen.

In dieser Hinsicht können wir uns an eines der Gesetze der Merphologie erinnern, das von einem bestimmten Dreisen als Wiederherstellungsgesetz bezeichnet wird :

Der Zeitpunkt der Verbesserung der Situation ist umgekehrt proportional zum Zeitpunkt ihrer Verschlechterung.

Die folgende Beobachtung wird als Beispiel gegeben: Das Verkleben der Vase dauert länger als das Zerbrechen. Dieses Gesetz beschreibt überraschend genau die Beziehung zwischen den charakteristischen Raten für den Relaxationsprozess eines stabilen Systems, die durch ein abnehmendes Exponentialgesetz beschrieben werden kann $$$e ^ {- \ lambda t}$ und die Entwicklungsrate des katastrophalen Prozesses in einem instabilen System in linearer Näherung - das exponentielle Wachstum einer kleinen Störung $$$e ^ {\ lambda t}$ . Diese Geschwindigkeiten sind tatsächlich umgekehrt proportional zueinander. Das Vasenbeispiel ist jedoch nicht Entspannung - ein Übergang in den wahrscheinlichsten Zustand. Es ist näher an einem anderen Prozess - an der Selbstorganisation wird dieser Prozess in erster Näherung durch das Logistikgesetz beschrieben und näher an der Entspannung als an der Katastrophe.

Typische instationäre Prozesse: Katastrophe, Entspannung und Selbstorganisation bei gleicher charakteristischer Zeit.

$$

$$* * *$$

Manchmal bin ich beim Gehen im Schnee überrascht, dass mir eine Schneeflocke auf die Nase fällt. Ich bin überrascht, dass die Wahrscheinlichkeit dieses Ereignisses vernachlässigbar war. Demnach zu urteilen, wurde sie hoch am Himmel über dem Pazifik geboren, kreiste in unregelmäßigen turbulenten Strömungen in der Wolke, fiel ständig in eine andere Richtung ... um an meine Nasenspitze zu gelangen! Und was für ein atemberaubender Weg reisten Photonen von einem fernen Stern! Zehntausende von Jahren stürmten sie durch das Universum, sie wurden nicht von Staub verschluckt, sie trafen keinen Asteroiden! Sie wurden in der Quantenwelt eines fernen Sterns geboren und beendeten ihre Reise in die Quantenwelt des Opsinproteins auf der Netzhaut in meinem Auge. Es macht keinen Sinn, auch nur die Wahrscheinlichkeit dieses Ereignisses zu berücksichtigen, es ist Null, aber das Ereignis passiert, und ich sehe das flackernde Licht eines Sterns. Jetzt ist klar, dass dies alles daran liegt, dass der Bereich meiner Nase und sogar die Moleküle ein Maß ungleich Null haben, aber immer noch erstaunlich: Was mit ziemlicher Sicherheit nicht hätte passieren dürfen, passiert immer noch!

Lassen Sie die Philosophen über das vorbestimmte oder zufällige Schicksal, die Wahrheit oder das Phantom unseres Naturwissens streiten. Ich fordere den Leser auf, die Welt von der Höhe der mathematischen Abstraktionen aus zu betrachten und ihre Schönheit und Beständigkeit zu bewundern.