Dreiwertige Logik
Liste der Erfolge
- Grundlegende ternäre Logikgatter: T_NOT, T_OR, T_AND, T_NAND, T_NOR, T_XOR und mehr
- Synthese, Minimierung und Realisierung für ternäre Funktionen
- Ternärer Halbaddierer, Ternärer Volladdierer, Ternärer Ripple-Carry-Addierer
- Ternärer Vollsubtrahierer, Komparator, Multiplikator, Multiplexer / Demultiplexer
- Ternäre Flip Flap Flops und Latches
- Eine primitive ternäre arithmetische und logische Einheit (ALU)
Konventionen und verwendete Technologien
- Bei der Implementierung wurde Unbalanced Ternary (0, 1, 2) verwendet
- 1 Trit wird durch 2 Bits ausgedrückt: 0 ~ 00, 1 ~ 01, 2 ~ 10 (11 ist undefiniert)
- ModelSim, Quartus Prime, Logisim
Einführung
Als Studienanfänger der Innopolis University hatten wir die Möglichkeit, Projekte während unseres Computerarchitekturkurses zu realisieren. Unsere Gruppe war besonders an dem ternären System und seiner Funktionsweise interessiert, daher beschlossen wir, ein einfaches ternäres System mit grundlegenden Komponenten (Gates) zu implementieren.
In der Logik ist eine dreiwertige Logik (auch trinäre Logik, dreiwertig, ternär) eines von mehreren vielwertigen Logiksystemen, in denen es drei Wahrheitswerte gibt, die wahr, falsch und einen unbestimmten dritten Wert anzeigen.
Die ternäre Logik ist MVL -konform (Multi-Valued Logic). Es werden jedoch nur drei logische Zustände verwendet, ' 0 ', ' 1 ' und ' 2 '. Der optimale Radix ( r ) einer Bruchzahl ist der natürliche Logarithmus ( e ). Die ternäre Logik verwendet die Zahlendarstellung mit r = 3 im Vergleich zur binären Logik, die r = 2 verwendet . Daher ist die Basis 3 der wirtschaftlichste ganzzahlige Radix, der dem natürlichen Logarithmus e am nächsten kommt. Diese spezielle Eigenschaft der Basis 3 inspirierte den frühen Computer Designer, um einen ternären Computer zu bauen.
Der erste funktionierende ternäre Computer wurde 1958 in Russland an der Moskauer Staatsuniversität gebaut. Der Computer wurde von Nikolay Brusentsov und seinen Kollegen entworfen. Sie nannten es Setun , wie der Fluss, der in der Nähe des Universitätscampus fließt.
Ternäre Logik
Eine ternäre Logikfunktion ist eine Abbildung F: {0,1,2} n -> {0,1,2} . Wir werden die Vor- und Nachteile der ternären Logik gegenüber der binären Logik diskutieren.
Wenn die Boolesche Logik 2 2 = 4 unäre Operatoren hat, führt das Hinzufügen eines dritten Werts in der ternären Logik zu insgesamt 3 3 = 27 verschiedenen Operatoren für einen einzelnen Eingabewert. Wenn die Boolesche Logik 2 2 2 = 16 verschiedene binäre Operatoren (Operatoren mit 2 Eingängen) hat, hat die ternäre Logik 3 3 2 = 19.683 solcher Operatoren. Wenn wir leicht einen signifikanten Bruchteil der Booleschen Operatoren benennen können (nicht und, oder, und, noch, ausschließlich oder, Äquivalenz, Implikation), ist es unvernünftig zu versuchen, alle bis auf einen kleinen Bruchteil der möglichen ternären Operatoren zu benennen.
Vorteile der ternären Logik
Eine ternäre Logikdarstellung ermöglicht eine kompaktere und effizientere Informationscodierung als die entsprechende binäre Logikdarstellung. Das angegebene Argument lautet wie folgt: Wenn wir annehmen, dass eine digitale Schaltung N mögliche Eingangskombinationen hat, benötigt eine binäre Schaltung log 2 N Eingangsleitungen und eine ternäre Schaltung log 3 N Eingangsleitungen.
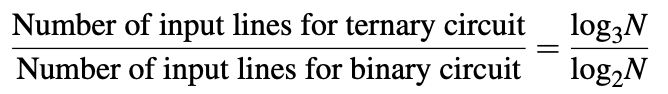

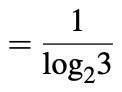

Daher sollte eine ternär codierte Implementierung einer gegebenen binären Logikfunktion das 0,63-fache der Eingabezeilen erfordern als die entsprechende binäre Implementierung.
Nachteile der ternären Logik
Obwohl ternäre Logikschaltungen weniger Eingangsleitungen als die entsprechenden binären Logikschaltungen erfordern sollten, sind ternäre Logikschaltungen derzeit keine praktische Wahl. Die Gründe sind
- Die Technologie zur Implementierung ternärer Hardware befindet sich noch in den Bereichen Theorie, Simulation und Labortest
- Die Darstellung von drei ternären Logikpegeln (0, 1 und 2) unter Verwendung der Spannungspegel der vorhandenen Technologie ist noch nicht effektiv definiert
- Es wird kein Rechenmodell und keine Programmiersprache entwickelt. Die Simulation der Ergebnisse der Implementierung ternärer Schaltkreise unter Verwendung von komplementären Metalloxidhalbleitern (CMOS), Resonanztunneldioden (RTD) und Kohlenstoff-Nanoröhrentechnologien zeigt jedoch, dass ternäre Logik eine Wahl für zukünftige Berechnungen sein kann.
Verschiedene mögliche Darstellungen für das ternäre System
- Ternäres Zahlensystem (Unausgeglichenes ternäres) , jede Ziffer ist ein Trit (trinäre Ziffer) mit einem Wert von: 0, 1 oder 2
- Ausgeglichen ternär , jede Ziffer hat einen von 3 Werten: -1, 0 oder +1; Diese Werte können auch auf -, 0, + vereinfacht werden (am häufigsten verwendet).
- Redundante binäre Darstellung , jede Ziffer kann einen Wert von -1, 0, 0/1 haben (der Wert 0/1 hat zwei verschiedene Darstellungen)
- Schräg-Binärzahlensystem , nur die höchstwertige Ziffer ungleich Null hat einen Wert 2, und die verbleibenden Ziffern haben einen Wert von 0 oder 1
Mehr zum ausgeglichenen ternären Nummerierungssystem
Heutzutage ist fast die gesamte Hardware für das binäre Rechnen ausgelegt. Wenn wir eine stabile elektronische Komponente mit drei stabilen Zuständen hätten, hätte sich die Welt vielleicht dem ternären Rechnen zugewandt. Dies ist jedoch heute nicht die Wahrheit. Die ausgeglichene ternäre Radixnotation hat einige vorteilhafte Eigenschaften:
- Die ternäre Inversion ist einfach, tauschen Sie einfach -1 gegen 1 aus und umgekehrt. Wenn wir ein Beispiel verwenden, wird 24 als 1T0 und -24 als T10 in ausgeglichener ternärer Notation dargestellt (T ist einfach eine Notation für -1). Dies ist einfacher als die Regel für das Zweierkomplement in der binären Logik.
- Das Vorzeichen einer Zahl wird durch das bedeutendste "Trit" ungleich Null angegeben.
- Der Vorgang des Rundens auf die nächste ganze Zahl ist identisch mit dem Abschneiden.
- Addition und Subtraktion sind im Wesentlichen dieselbe Operation (dh Sie addieren lediglich die Ziffern nach den Regeln für die Addition von Ziffern).
Beispiele:
21 10 = 1T10 3 ; 296 10 = 11T00T 3 ;
-24 10 = T10 3 ; -137 10 = T110T1 3
Ternäre Arithmetik
Ternäre Arithmetik kann eine kompaktere Notation bieten als binäre Arithmetik und wäre eine naheliegende Wahl gewesen, wenn die Hardwarehersteller einen ternären Schalter gefunden hätten.
Ausgewogene ternäre Addition und Multiplikation
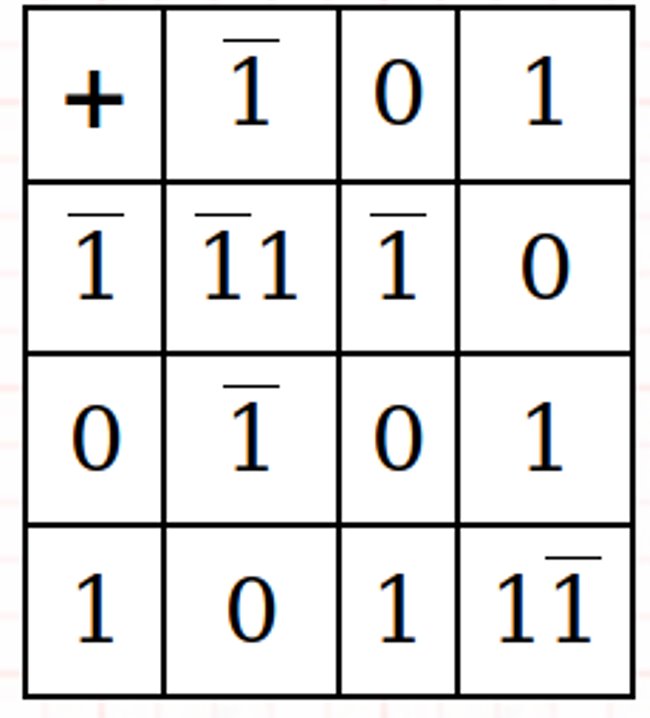
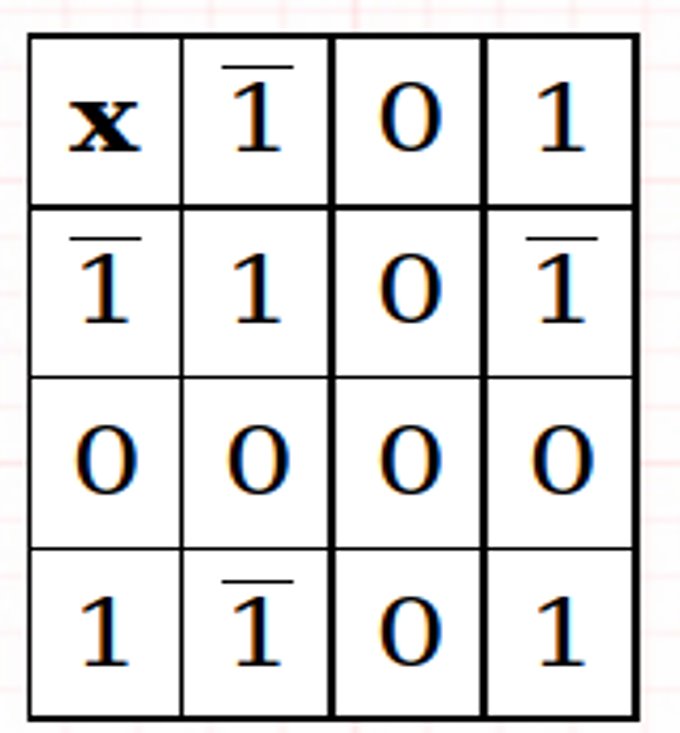
Beispiele:
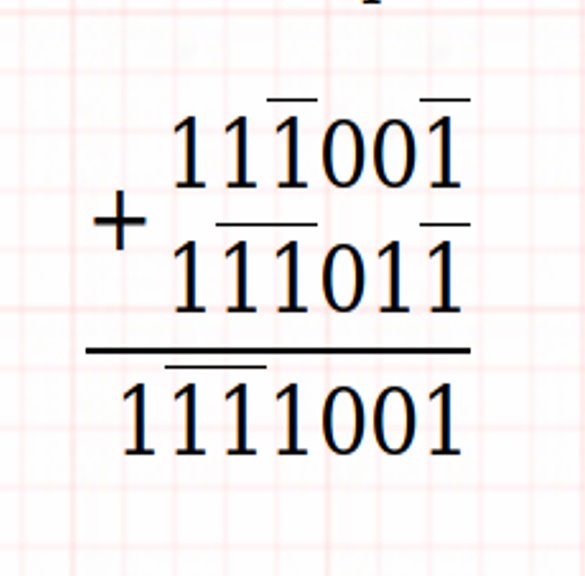
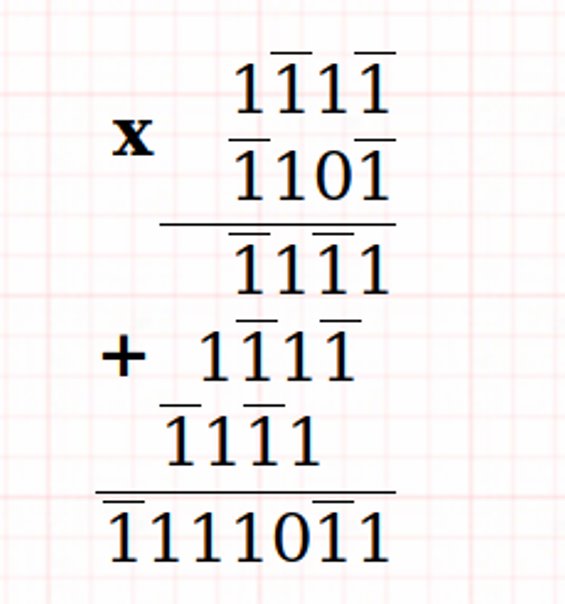
Ternäre Kombinationsschaltungen (Ternäre Tore)
Eine Kombinationsschaltung besteht aus Eingangsvariablen, ternären Logikgattern und Ausgangsvariablen. Der Ausgang der Schaltung hängt nur vom aktuellen Eingang ab. Logikgatter akzeptieren Signale von den Eingangsvariablen und erzeugen Ausgangssignale. Dieser Prozess transformiert ternäre Informationen aus
die angegebenen Eingabedaten zu den erforderlichen ternären Ausgabedaten.
Wie oben erwähnt, können wir leicht einen signifikanten Bruchteil der Booleschen Operatoren benennen (nicht und oder, und, noch, ausschließlich oder, Äquivalenz, Implikation), es ist jedoch unvernünftig zu versuchen, alle bis auf einen kleinen Bruchteil der möglichen zu benennen ternäre Operatoren. Wir werden die folgenden ternären Schaltkreise betrachten:
Und (Min) : Es ist natürlich, den Booleschen Wert und die Funktion auf eine ternäre Funktion zu erweitern, indem erklärt wird, dass das Ergebnis nur dann wahr ist, wenn beide Eingaben wahr sind, falsch, wenn eine Eingabe falsch ist, und ansonsten unbekannt.
Und Schaltung / Wahrheitstabelle Oder (Max) : Es ist auch natürlich, den Booleschen Wert oder die Funktion auf ternär zu erweitern, indem erklärt wird, dass das Ergebnis wahr ist, wenn eine Eingabe wahr ist, falsch nur, wenn beide Eingaben falsch sind, und ansonsten unbekannt.
Oder Schaltung / Wahrheitstabelle Konsens : In der Booleschen Logik ist die Umkehrung von exklusiv oder wahr, wenn die beiden Eingaben gleich sind, und falsch, wenn sie unterschiedlich sind. Es gibt mehrere natürliche Erweiterungen dieser Idee für die ternäre Logik. Eine davon ist der logische Konsens einer Reihe von Variablen, der wahr ist, wenn alle wahr sind, falsch, wenn alle falsch sind und ansonsten unbekannt
Konsensschaltung / Wahrheitstabelle Beliebig : Wenn der Konsens erfordert, dass beide Eingaben übereinstimmen, bevor etwas anderes als unbekannt behauptet wird, erklärt der Operator "Alles akzeptieren" nur dann eine unbekannte Schlussfolgerung, wenn beide Eingaben unbekannt sind oder aktiv nicht übereinstimmen. Andernfalls springt es zu einer Schlussfolgerung aus einer nicht unbekannten Eingabe, die ihm zur Verfügung steht.
Beliebige Schaltung / Wahrheitstabelle Inkrementieren und Dekrementieren : In der Booleschen Logik kann der Wechselrichter als Inkrementieren oder Dekrementieren seines Arguments Modulo 2 angesehen werden. Interne Logik, die Modulo 3-Inkrementierungs- und Dekrementierungsfunktionen unterscheiden sich stark von der Inversion.
Inkrement- und Dekrementschaltung Synthese, Minimierung und Realisierung für ternäre Funktionen
Beziehungen, die im ternären Logiksystem miteinander zusammenhängen
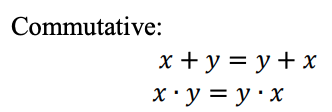
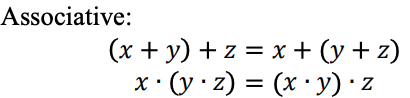
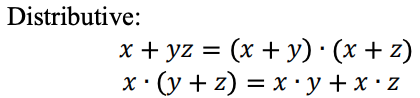
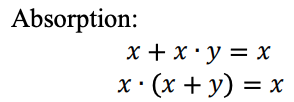
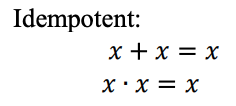
Eine ternäre Logikfunktion kann als Max-Min-Ausdruck dargestellt werden. Ternäre Max-Min-Ausdrücke sind wie folgt definiert:
Variable : Jedes Symbol, das einen Wert aus der Menge T ∈ {0,1,2} annimmt, ist eine ternäre Variable.
Literal : Literale sind transformierte Formen einer Variablen. Sie werden verwendet, um Max-Min-Ausdrücke zu bilden.
In der Literatur werden üblicherweise zwei Arten von Literalen verwendet: 1-reduzierte Post-Literale und 2-reduzierte Post-Literale. Ein 1-reduziertes Post-Literal einer Variablen x wird als x i dargestellt , wobei i ∈ {0,1,2} ist. Wenn x = i, dann ist x i = 1, andernfalls ist x i = 0. Die 1-reduzierten Post-Literale einer Variablen sind unten gezeigt.
Ein 2-reduziertes Post-Literal einer Variablen x wird als x i dargestellt , wobei i ∈ {0,1,2} ist. Wenn x = i, dann ist x i = 2, andernfalls ist x i = 0. Die 2-reduzierten Post-Literale einer Variablen sind unten gezeigt. In diesem Beispiel werden verschiedene Sätze von Literalen verwendet, um Max-Min-Ausdrücke zu bilden, wie zuvor erläutert.
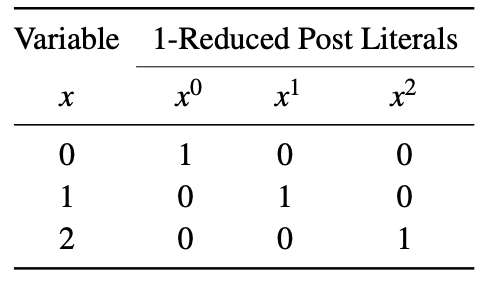
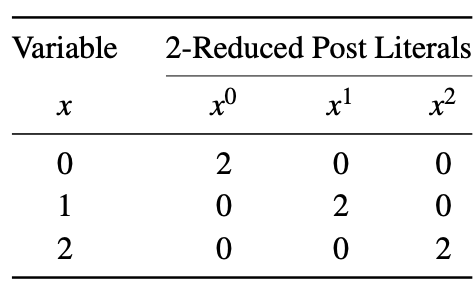
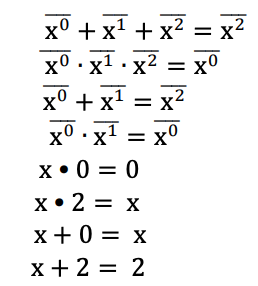
Minterm : Wenn Literale von Variablen einer Funktion mit der Min-Operation kombiniert werden, wird der Begriff als Minterm bezeichnet. Zum Beispiel sind für eine ternäre Logikfunktion mit drei Variablen F (x, y, z) xyz und xz zwei Beispiele für Zwischenzeiten.
Max-Min-Ausdruck : Wenn zwei oder mehr Intervalle mit Max-Operationen kombiniert werden, wird der Ausdruck als Max-Min-Ausdruck (Max-Min) bezeichnet. Beispielsweise ist für eine ternäre Logikfunktion mit 3 Variablen F (x, y, z) = xy + yz + xyz ein Beispiel für einen Max-Min-Ausdruck.
Jede Funktion F (x, y, z) kann immer als dargestellt werden
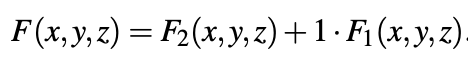
Drei grundlegende Methoden zur Minimierung ternärer Funktionen sind:
- Manipulation des Algebraausdrucks wie in der Booleschen Algebra.
- Die tabellarische Methode.
- Ternäre K. Kartenmethode.
Für die Implementierung von ternären Schaltkreisen ist es erforderlich, ternäre Variablen in unäre Variablen umzuwandeln (unter Verwendung der Tabelle 2-Reduced Post Literals).
Ternärer Halbaddierer
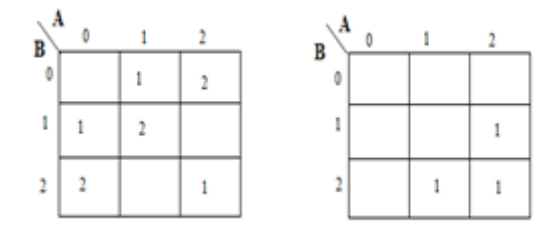
Eine Schaltung für die Addition von zwei 1-Trit-Zahlen wird als Halbaddierer bezeichnet. Die Schaltung berücksichtigt keinen Übertrag, der in der vorherigen Addition erzeugt wurde. Der Additionsprozess im ternären Logiksystem ist unten gezeigt. Hier sind A und B zwei Eingänge und Summe (S) und Übertrag (CARRY)
sind zwei Ausgänge.
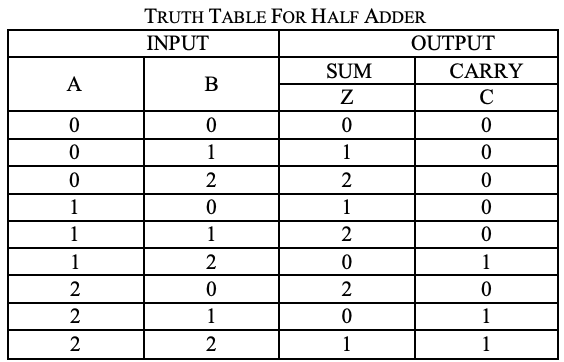
Analyse
Eine Karnaugh-Karte (K-Karte) wird verwendet, um die Summe darzustellen und die Ausgabe zu übertragen. K-Maps sind nützlich zur Minimierung und Optimierung von Logikschaltungen. Hier wird eine K-Map mit 2 Eingängen verwendet. Da keine Gruppierung von 2 und 1 möglich ist, ist die Ausgangsgleichung wie folgt.
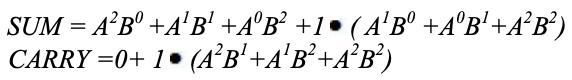
Implementierung
Ternäre Halbaddiererschaltung / Verilogmodule half_adder ( input [1:0] A, [1:0] B, output [1:0] sum, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; wire [1:0] c0, c1, c2, c3; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a2,b0,i0); andgate and_2(a1,b1,i1); andgate and_3(a0,b2,i2); // partial products orgate or_1(i0, i1, o0); orgate or_2(o0, i2, o1); // f1 andgate and_4(a1,b0,i3); andgate and_5(a0,b1,i4); andgate and_6(a2,b2,i5); // partial products orgate or_3(i3, i4, o2); orgate or_4(o2, i5, o3); // f2 andgate and_7(o3,temp,o4); // 1.f2 andgate andc_0(a2,b1,c0); andgate andc_1(a1,b2,c1); orgate orc_0(c0,c1,c2); orgate orc_1(c2,i5,c3); andgate andc_2(c3,temp,carry); // carry orgate or_5(o1, o4, sum); // sum endmodule
Ternärer Volladdierer
Wie bei Halbaddierern kann eine Stufe eines ternären Volladdierers durch eine numerische Tabelle beschrieben werden, die die Summe SUMME angibt und CARRY als Funktion der drei Eingänge A, B zusammen mit dem Übertrag in C ausführt :
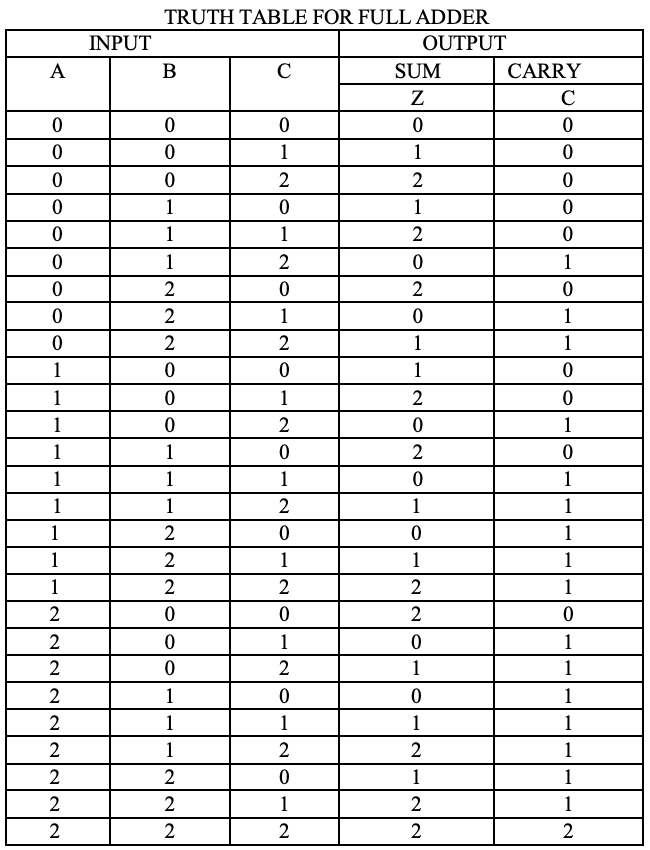
Analyse
Eine Karnaugh-Karte (K-Karte) wird verwendet, um die Summe darzustellen und die Ausgabe zu übertragen. K-Maps sind nützlich zur Minimierung und Optimierung von Logikschaltungen. Hier wird eine K-Map mit 3 Eingängen verwendet.
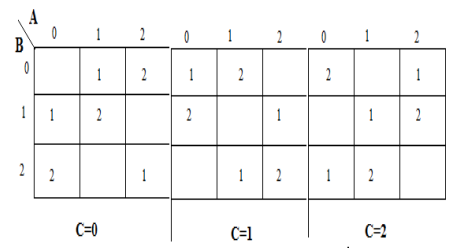
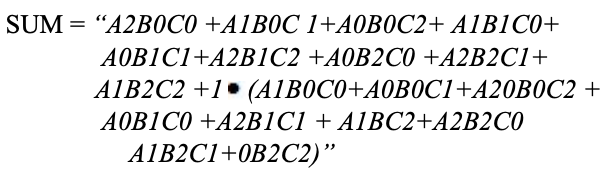
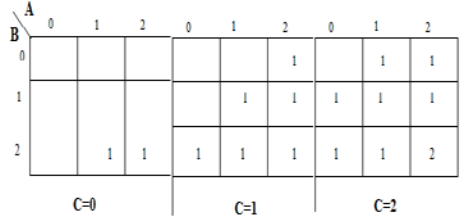
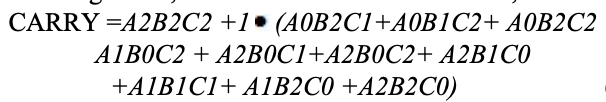
Implementierung
Ternäre Volladdiererschaltung / Verilog module ternary_full_adder ( input [1:0] A, [1:0] B, [1:0] c_in, output [1:0] sum, [1:0] c_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b00; wire [1:0] a0, a1, a2, b0, b1, b2, a20; wire [1:0] i0, i1, i2, i3, i4; wire [1:0] i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] o0, o1, o2, o3, o4, o5, o6, o7, o8, o9; wire [1:0] c0, c1, c2; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12, t13, t14, t15, t16; wire [1:0] g0, g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15; mask mk_1(A, a0, a1, a2); mask mk_2(B, b0, b1, b2); mask mk_3(c_in, c0, c1, c2); andgate3 and3_1(a2,b0,c0, i0); andgate3 and3_2(a1,b0,c1, i1); andgate3 and3_3(a0,b0,c2, i2); andgate3 and3_4(a1,b1,c0, i3); andgate3 and3_5(a0,b1,c1, i4); andgate3 and3_6(a2,b1,c2, i5); andgate3 and3_7(a0,b2,c0, i6); andgate3 and3_8(a2,b2,c1, i7); andgate3 and3_9(a1,b2,c2, i8); andgate3 and3_10(a1,b0,c0, i9); andgate3 and3_11(a0,b0,c1, i10); orgate or__(a2, a0, a20); andgate3 and3_12(a20,b0,c2, i11); // note a20 andgate3 and3_13(a0,b1,c0, i12); andgate3 and3_14(a2,b1,c1, i13); andgate3 and3_15(a1,B,c2, i14); andgate3 and3_16(a2,b2,c0, i15); andgate3 and3_17(a1,b2,c1, i16); andgate3 and3_18(temp2,b2,c2, i17); orgate or_1(i9, i10, o0); orgate or_2(o0, i11, o1); orgate or_3(o1, i12, o2); orgate or_4(o2, i13, o3); orgate or_5(o3, i14, o4); orgate or_6(o4, i15, o5); orgate or_7(o5, i16, o6); orgate or_8(o6, i17, o7); andgate and_1(o7, temp1, o8); // 1.f2 orgate or_9(i0, i1, h0); orgate or_10(h0, i2, h1); orgate or_11(h1, i3, h2); orgate or_12(h2, i4, h3); orgate or_13(h3, i5, h4); orgate or_14(h4, i6, h5); orgate or_15(h5, i7, h6); orgate or_16(h6, i8, h7); orgate or_17_(h7, o8, sum); // sum // carry andgate3 and3_19(a2,b2,c2, t0); // f1 andgate3 and3_20(a0,b1,c2, t1); andgate3 and3_21(a0,b2,c2, t2); andgate3 and3_22(a0,b2,c1, t3); andgate3 and3_23(a1,b2,c0, t4); andgate3 and3_24(a2,b2,c0, t5); andgate3 and3_25(a1,b1,c1, t6); andgate3 and3_26(a1,b2,c1, t7); andgate3 and3_27(a1,b0,c2, t8); andgate3 and3_28(a1,b1,c2, t9); andgate3 and3_29(a1,b2,c2, t10); andgate3 and3_25_(a2,b0,c2, t11); andgate3 and3_26_(a2,b1,c2, t12); andgate3 and3_27_(a2,b0,c1, t13); andgate3 and3_28_(a2,b1,c1, t14); andgate3 and3_29_(a2,b2,c1, t15); andgate3 and3_9_(a2,b1,c0, t16); orgate or_17(t1, t2, g0); orgate or_18(g0, t3, g1); orgate or_19(g1, t4, g2); orgate or_20(g2, t5, g3); orgate or_21(g3, t6, g4); orgate or_22(g4, t7, g5); orgate or_23(g5, t8, g6); orgate or_24(g6, t9, g7); orgate or_25(g7, t10, g8); orgate or_21_(g8, t11, g9); orgate or_22_(g9, t12, g10); orgate or_23_(g10, t13, g11); orgate or_24_(g11, t14, g12); orgate or_25_(g12, t15, g13); orgate or_5_(g13, t16, g14); //f2 andgate and_2(g14, temp1, g15); // 1.f2 orgate or_26(g15, t0, c_out); // carry endmodule
Ternärer Vollsubtrahierer
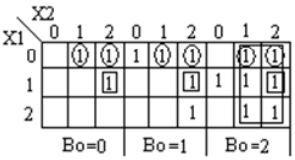
Der ternäre Vollsubtrahierer ist eine Schaltung, die zwei Eingänge und das vorherige Ausleihen subtrahiert. Die Wahrheitstabelle für den Subtrahierer ist unten gezeigt

Analyse und Implementierung des ternären Vollsubtrahierers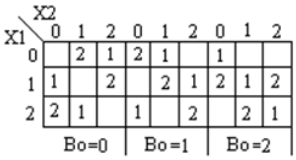
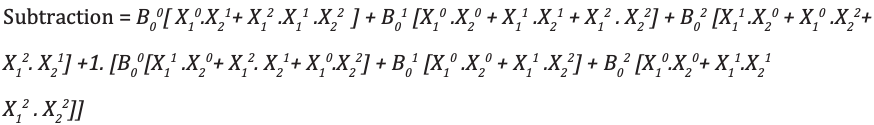
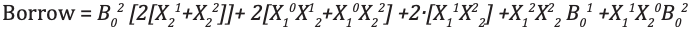
Code module full_subtractor( input [1:0] P, Q, b_in, output [1:0] diff, b_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b10; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] c0, c1, c2, c3; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7, h8, h9, h10, h11; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9; wire [1:0] p0, p1, p2; wire [1:0] q0, q1, q2; mask mk_1(P, p0, p1, p2); mask mk_2(Q, q0, q1, q2); mask mk_3(b_in, b0, b1, b2); andgate and_0(p0, q1, i0); andgate3 and3_0(p2, p1, q2, i1); orgate or_0(i0, i1, i2); andgate and_1(b0, i2, i3); // first expression andgate and_2(p0, q0, i4); andgate and_3(p1, q1, i5); andgate and_4(p2, q2, i6); orgate or_1(i4, i5, i7); orgate or_2(i7, i6, i8); andgate and_5(i8, b1, i9); // second expression andgate and_6(p1, q0, i10); andgate and_7(p0, q2, i11); andgate and_8(p2, q1, i12); orgate or_3(i10, i11, i13); orgate or_4(i13, i12, i14); andgate and_9(i14, b2, i15); // third expression orgate or_5(i3, i9, i16); orgate or_6(i16, i15, c0); //f1 orgate or_7(i10, i12, t0); orgate or_8(t0, i11, t1); andgate and_10(t1, b0, t2); // 1 expression andgate and_11(p1, q2, i17); orgate or_9(i4, i17, t3); andgate and_12(t3, b1, t4); // 1- expression orgate or_10(i4, i5, t5); orgate or_11(t5, i6, t6); andgate and_12_(t6, b2, t7); // 1-- expression orgate or_12(t2, t4, t8); orgate or_13(t8, t7, t9); andgate and_13(t9, temp1, c1); orgate or_14(c0, c1, diff); // difference orgate or_15(q1, q2, h0); andgate and_14(h0, temp2, h1); andgate and_15(h1, b2, h3); // 1 b orgate or_16(i0, i11, h4); andgate and_16(h4, temp2, h5); // 1- b andgate and_17(i17, temp2, h6); // 1-- b andgate3 and3_1(p2, q2, b1, h7); // 1--- b andgate3 and3_2(p1, q0, b2, h8); // 1---- b orgate or_17(h3, h5, h9); orgate or_18(h9, h6, h10); orgate or_19(h10, h7, h11); orgate or_20(h11, h8, b_out); // borrow endmodule
Ternary Ripple Carry Addierer
Ripple-Carry-Addierer (RCA) ist eine bekannte Schaltung zum Addieren von zwei Zahlen durch Kaskadieren von ternären Volladdierern. Ein ternärer RCA ist seinem binären Gegenstück ziemlich ähnlich. Ein ternärer Halbaddierer wird verwendet, um die am wenigsten signifikanten ternären Ziffern hinzuzufügen. Der Rest wird von Ternary Full Adders zusammengefasst. Wie bereits erwähnt, fügt Ternary Full Adder drei ternäre Eingabevariablen hinzu.
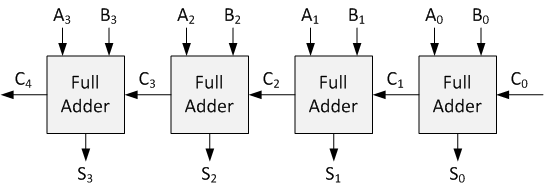
Implementierung
Verilog-Code: Ternärer Ripple-Carry-Addierer module ternary_ripple_adder ( input [15:0] input1 , input [15:0] input2 , output [15:0] out , output [1:0] overflow_trit ); wire [15:0] carry ; reg tem; assign carry[0] = tem; assign carry[1] = tem; always @(input1, input2) begin tem <= 1'b0; end generate genvar i; for (i = 0; i <= 12; i=i+2) begin full_add af({input1[i+1],input1[i]}, {input2[i+1],input2[i]}, {carry[i+1],carry[i]}, {out[i+1], out[i]}, {carry[i+3],carry[i+2]}); end full_add af({input1[15],input1[14]}, {input2[15],input2[14]}, {carry[15],carry[14]}, {out[15], out[14]}, overflow_trit); endgenerate endmodule
Ternäre Komparatoren
Ternäre Komparatorschaltung Camper zwei Eingänge X 1 , X 2 und erzeugt dementsprechend Ausgang als X 1 = X 2 , X 1 > X 2 , X 1 <X 2 . Die Wahrheitstabelle für einen ternären Komparator ist unten gezeigt
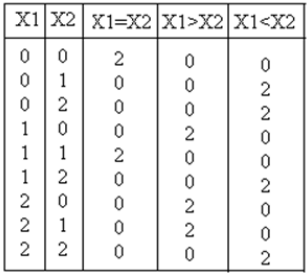
Analyse und ImplementierungDie Ausgangsgleichung für X 1 = X 2 , X 1 > X 2 , X 1 <X 2 lautet:
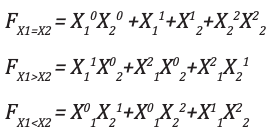
Entsprechende k-Maps sind unten dargestellt

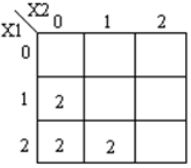
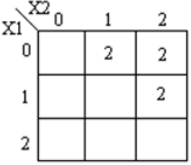
Code module ternary_comparators ( input [1:0] x1, x2, output [1:0] f1, f2, f3 ); wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7; wire [1:0] h0, h1, h2, h3, h4, h5; wire [1:0] x10, x11, x12; wire [1:0] x20, x21, x22; mask mk_1(x1, x10, x11, x12); mask mk_2(x2, x20, x21, x22); andgate and_0(x10, x20, t0); andgate and_1(x22, x22, t1); orgate or_0(t0, t1, h0); orgate or_1(h0, x11, h1); orgate or_2(h1, x21, f1); // x1 == x2 andgate and_2(x11, x20, t2); andgate and_3(x12, x20, t3); andgate and_4(x12, x21, t4); orgate or_3(t2, t3, h3); orgate or_4(h3, t4, f2); // x1>x2 andgate and_5(x10, x21, t5); andgate and_6(x10, x22, t6); andgate and_7(x11, x22, t7); orgate or_5(t5, t6, h4); orgate or_6(h4, t7, f3); // x1<X2 endmodule
Ternärer Multiplikator
Der ternäre Multiplikator ist eine Schaltung, die zwei Eingangszahlen multipliziert und ein entsprechendes Produkt erzeugt. Die Wahrheitstabelle für diese Schaltung ist unten gezeigt:
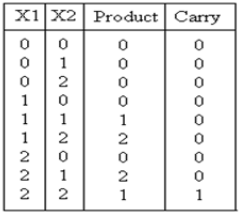
Analyse und ImplementierungDer resultierende Ausdruck für das Produkt und den Carry wird angezeigt:
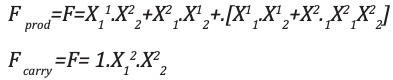
Die entsprechenden K-Maps werden angezeigt:
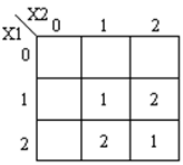
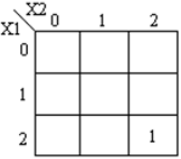
Code module ternary_multiplier ( input [1:0] A, [1:0] B, output [1:0] product, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a1,b2,i0); andgate and_2(a2,b1,i1); orgate or_1(i0, i1, o0); // f1 andgate and_4(a1,b1,i3); andgate and_5(a2,b2,i4); orgate or_3(i3, i4, o2); andgate and_3(temp,o2,o3); orgate or_4(o3, o0, product); // product andgate andc_0(a2,b2,o4); andgate andc_1(temp,o4,carry); // carry endmodule
Ternäre Multiplexer und Demultiplexer
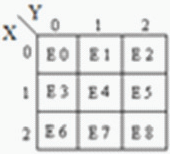
Multiplexer ist eine Schaltung mit mehreren Eingängen und einem einzigen Ausgang. Es ist auch als Decoder bekannt. Die Ausgangsfunktion des Multiplexers wird durch die Anzahl der Funktionsleitungen bestimmt. Also für 2 trit
Multiplexer der Ausgang ist 3 2 = 9 und zwei sind die Funktionsauswahlleitungen. Multiplexer dh Funktion
Auswahllogik wählt 1 von 9 Funktionen als Ausgang aus. Die Funktionsauswahllogik wird unter Verwendung von Logikgattern implementiert. Die Ausgangsgleichung der Funktionsauswahllogik lautet:
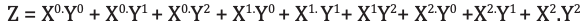
Analyse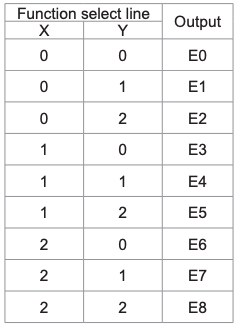
Demultiplexer wird auch als Encoder bezeichnet. Seine Funktionalität ist umgekehrt zu der des Multiplexers. Es akzeptiert den einzelnen Eingang und verteilt ihn auf mehrere Ausgänge
Einfache ternäre Verriegelung
Obwohl der Entwurf von Schaltungen, die eine kombinatorische ternäre Logik implementieren, unkompliziert ist, war der Entwurf eines einfachen und robusten ternären Speicherelements (dh eines Latch), das für die Implementierung einer integrierten Schaltung (IC) geeignet ist, eine Herausforderung. Ein einfacher ternärer Latch kann jedoch erhalten werden, indem die verwendeten binären NOR- oder NAND-Gatter durch entsprechende ternäre T_NOR- oder T_NAND-Gatter ersetzt werden.
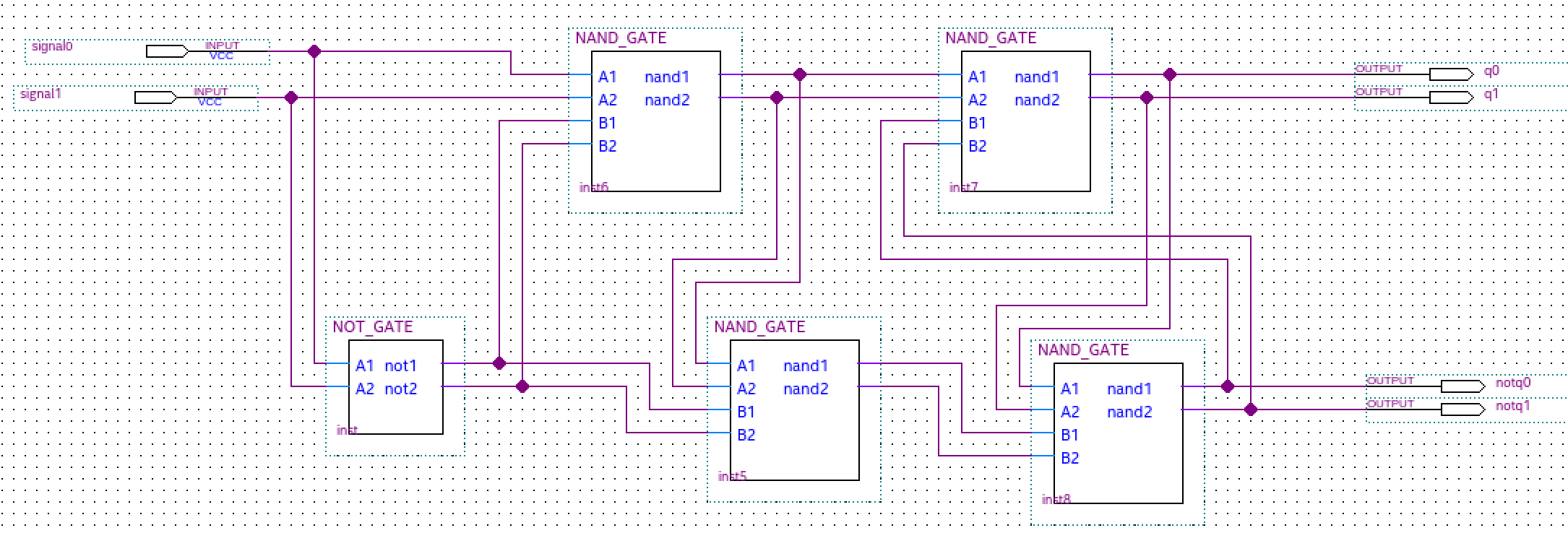
Einfacher ternärer D Flip-Flap-Flop
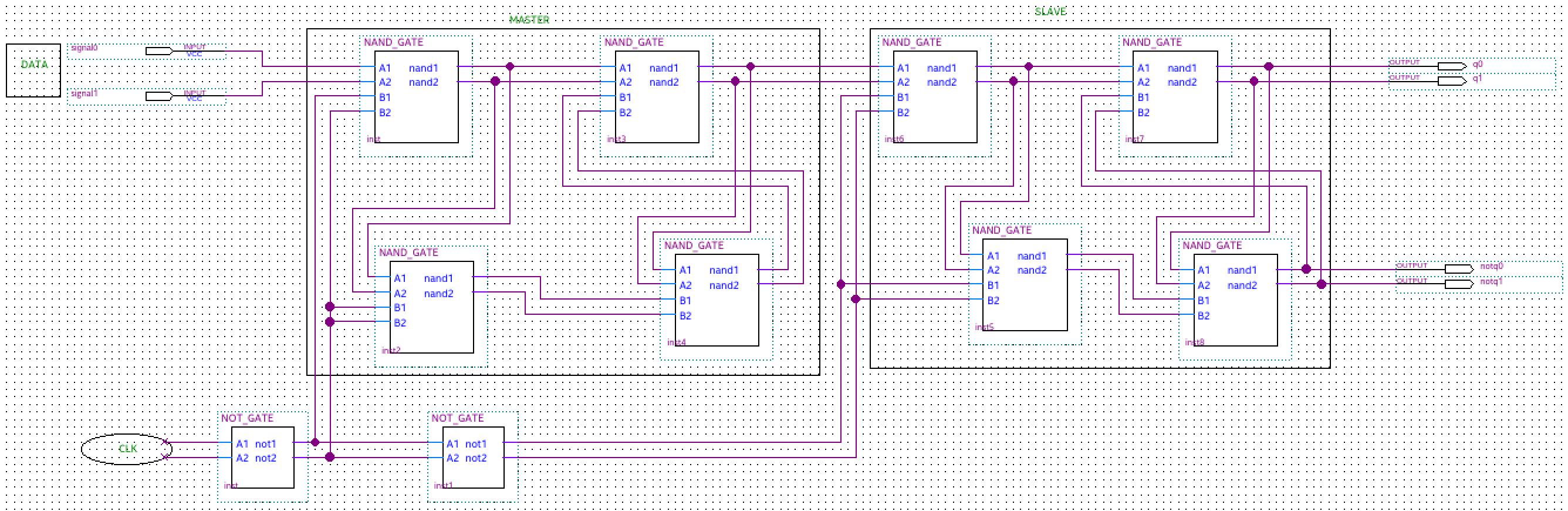
Das ternäre D-Flip-Flap-Flop (FFF) des Master-Slave (MS) wird basierend auf den ternären D-Latches realisiert. Dies ähnelt der Art und Weise, wie das binäre D-Flip-Flop (FF) unter Verwendung von binären D-Latches realisiert wird. Das Logikdiagramm und die Betriebsbeschreibung des MS-Binär-D-Flipflops sind bekannt. Um das ternäre MS- FFF zu implementieren, ersetzen wir die binären D-Latches durch ternäre D-Latches (realisiert mit ternären Negated-Minimun-Gates zweier Eingänge - NAND) und die binären Inverter durch einfache ternäre Inverter (STI). Die Wahrheitstabellen sowohl für die ternären NAND-Schaltungen als auch für die ternären STI-Schaltungen werden angezeigt
Wahrheitstabelle für Nand- und Sti-Schaltungen Für MS ternäre D FFF mit binärem Takt sind die Daten ternär (0, 1 und 2 Logik) und der Takt ist binär (niedrig und hoch - in unserem
Implementierung, 0 und 2 Logik). Die MS ternäre D FFF mit
Die binäre Uhr kann die Daten lesen, wenn die Uhr von niedrig nach geht
hoch (positive Flanke) oder von hoch nach niedrig (negative Flanke), je nachdem
auf die Anzahl der STIs.
Die Eingänge des ternären D FFF sind Data und Clk, und die Ausgänge sind Q und Not_Q. Das Taktsignal ist binär und die Logikpegel werden mit 0 und 2 bezeichnet, um die Entsprechung mit der elektrischen Implementierung aufrechtzuerhalten
Ternäre 1-Bit-Arithmetik- und Logikeinheit (T-ALU)
Die Ternary Arithmetic Logic Unit (ALU) ist eine digitale Schaltung, mit der arithmetische und logische Operationen ausgeführt werden. Es stellt den Grundbaustein der Central Processing Unit (CPU) eines ternären Computers dar. ALU führt arithmetische Operationen wie Addition, Subtraktion, Multiplikation und Vergleich von logischen Operationen, NAND, NOR, NOT, AND und OR aus. Unten ist eine primitive Architektur einer 1-Trit-ALU gezeigt
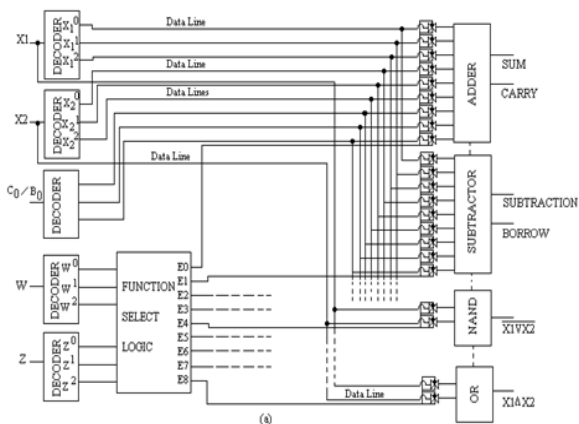
Wahrheitstabelle und Funktionsweise für T-ALU Grundbausteine der ALU sind Decoder, Funktionsauswahllogik (Multiplexer), Übertragungsgatter und separate Verarbeitungsmodule. Die Funktionsauswahllogik wählt 1 von 9 aufgelisteten Funktionen aus, abhängig vom Logikzustand auf den Funktionsauswahlleitungen W und Z.
Ausgangsleitungen der Auswahllogik sind mit TG (Ternary Gate) verbunden, das jedem Modul zugeordnet ist. Jedes Modul wird nur ausgewählt, wenn die zugehörige TG aktiviert ist, andernfalls ist es von Datenleitungen isoliert. Wenn beispielsweise die Eingabe von den Auswahlleitungen W und Z = 0 ist, ist die Ausgabe E 0 der Auswahllogik hoch (2), während E 1 bis E 8 niedrig (0) ist, so dass die dem Addierermodul zugeordnete TG aktiviert wird, um Daten zuzulassen
Leitungen, die an Addierermodule angeschlossen werden sollen, während andere Module von den Datenleitungen isoliert sind.
Schließlich kann durch Kaskadieren von n / 2 Trit-ALU-Schichten eine N- Trit-ALU gebildet werden.