Einführung
Wir haben einen synthetisierbaren Verilog-Code zur Berechnung einer ganzzahligen Kubikwurzel einer ganzzahligen Zahl über einen binären Suchalgorithmus erstellt. Dieser Code wurde auf einer Cyclone IV FPGA-Karte getestet. Hier können Sie über die Implementierung lesen und verstehen, wie die Dinge funktionieren.
Github-Link:
KubikwurzelWas ist eine Kubikwurzel?
Die Kubikwurzel einer Zahl
y ist eine Zahl
x, so dass
$$ display $$ x ^ 3 = y $$ display $$
Beispiele:
$$ display $$ \ sqrt [3] {8} = 2 \\ \ sqrt [3] {27} = 3 \\ \ sqrt [3] {64} = 4 $$ display $$
In unserer Implementierung verwenden wir also eine
ganzzahlige Kubikwurzel .
Dies bedeutet, dass eine Kubikwurzel einer Ganzzahl
x eine andere Ganzzahl
a ist, so dass:
$$ Anzeige $$ a ^ 3 \ leqslant x, \\ (a + 1) ^ 3 \ geqslant x $$ Anzeige $$
Beispiele:
$$ display $$ \ sqrt [3] {26} = 2 \\ \ sqrt [3] {28} = 3 \\ \ sqrt [3] {63} = 3 \\ \ sqrt [3] {65} = 4 $$ Anzeige $$
Hauptlogik
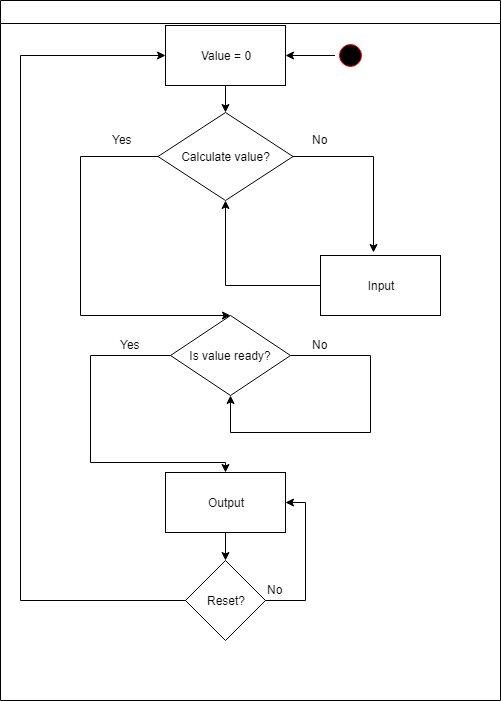
Das Hauptmodul ist für alle Aktionen mit einer Nummer während der Eingabe verantwortlich.
Es gibt 4 mögliche Aktionen:
- Inkrement mit 10 multiplizieren
- Inkrement durch 10 teilen (Inkrement ist immer nicht kleiner als 1)
- Anzahl erhöhen
- Anzahl verringern
Hauptmodulmodule cube_root( input inc, input sub, input next, input prev, input enter, input clk, output wire [7:0] leds, output wire [7:0] control ); reg signed [31:0] exit; wire ready; wire [31:0] res; reg zero = 0; // input // reg inc1 = 0; reg next1 = 0; reg prev1 = 0; reg sub1 = 0; reg enter1 = 0; reg [31:0] decimal = 1; ////////// reg [31:0] to_display; display_bcd display( .clk(clk), .value(ready == 0 ? exit : res), .control(control), .leds(leds) ); calculate calc( .clk(clk), .ready_to_calc(~enter), .num(exit), .ready(ready), .res(res) ); always @(posedge clk) begin if (enter == 1) begin if ((inc1 == 1'b0) && (~inc == 1'b1)) begin exit = exit + decimal; end inc1 = ~inc; if ((sub1 == 1'b0) && (~sub == 1'b1)) begin if (exit > 0) begin exit = exit - decimal; end end sub1 = ~sub; if ((next1 == 1'b0) && (~next == 1'b1)) begin decimal = decimal * 10; end next1 = ~next; if ((prev1 == 1'b0) && (~prev == 1'b1)) begin if (decimal >= 1 && decimal <= 9) begin decimal = 1; end else begin decimal = decimal / 10; end end prev1 = ~prev; end else begin if (ready == 1'b1) begin exit = 0; decimal = 1; end end end endmodule
Im Hauptmodul
cube_root gibt es noch zwei weitere Module:
berechne und
display_bcd . Das erste Modul führt alle erforderlichen Berechnungen durch, während das zweite Modul für die Anzeige der Eingabe- und Ausgabewerte während der Programmausführung verantwortlich ist.
Lassen Sie uns nun verstehen, wie sie funktionieren.
Modul berechnen
Das Berechnungsmodul verwendet einen binären Suchalgorithmus. Wenn alle Berechnungen abgeschlossen sind, wird die
Bereitschaftsvariable auf 1 gesetzt. Dies ist ein Signal für das Anzeigemodul, die Antwort auszugeben.
Modul berechnen module calculate( input clk, input ready_to_calc, input [31:0] num, output reg ready, output [31:0] res ); integer mid; integer start; integer final; integer counter; assign res = mid; always @(posedge clk) begin if (ready_to_calc == 1) begin if (ready == 0) begin mid = (start + final )/2; if ((mid*mid*mid) > num) begin final = mid; end else begin start = mid; end if (counter == 27) begin ready = 1; counter = 0; end else begin counter = counter + 1; end end end else begin final = 465; start = 0; ready = 0; counter = 0; end end endmodule
Warum führt dieses Modul genau 27 Iterationen aus?- Die maximale Eingabenummer ist 99999999. Die maximal mögliche Anzahl von Iterationen beträgt also
$ inline $ \ log_2 99999999 = 26.575424745 \ ca. 27 $ inline $
Warum wird die Obergrenze der binären Suche mit 465 initialisiert?- Weil es die maximale Anzahl ist, die wir als Ergebnis erhalten können.
$ inline $ \ sqrt [3] {99999999} \ ca. 464 $ inline $
Anzeigemodul
Dieses Modul ist für die Leistung verantwortlich. Es werden acht Acht-Segment-Anzeigen verwendet, die über 16 Pins bedient werden. Wenn 8 Pins für bestimmte ausgestellte LEDs "verantwortlich" sind und andere 8 Steuersegmente Steuersegmente sind, repräsentieren sie unterschiedliche Ziffern.
Wir übergeben diesem Modul also einen ganzzahligen Wert, den wir anzeigen möchten. Anschließend wird dieser Wert an das Modul
Binary_to_BCD übergeben, das die Binärzahl mithilfe des
Double Dabble-Algorithmus in die binär codierte Dezimalzahl konvertiert. Danach wird der konvertierte Wert einfach angezeigt.
Anzeigemodul module display_bcd ( input clk, input [31:0] value, output [7:0] control, output [7:0] leds ); bcd_convert #(32, 8) bcd_convert( .i_Clock(clk), .i_Binary(value_temp), .i_Start(1'b1), .o_BCD(bcd_number), .o_DV(bcd_ready) ); integer delay = 0; integer final_bcd; reg [2:0] ctrl = 0; reg [4:0] digit; wire bcd_ready; wire [31:0] bcd_number; wire [31:0] digits; assign digits = final_bcd; wire [31:0] value_temp; assign value_temp = value; assign control = ~(1 << ctrl); assign leds = ~ (digit == 0 ? 8'b00111111 : (digit == 1 ? 8'b00000110 : (digit == 2 ? 8'b01011011 : (digit == 3 ? 8'b01001111 : (digit == 4 ? 8'b01100110 : (digit == 5 ? 8'b01101101 : (digit == 6 ? 8'b01111101 : (digit == 7 ? 8'b00000111 : (digit == 8 ? 8'b01111111 : (digit == 9 ? 8'b01101111 : 8'b00000000)))))))))); always @(posedge clk) begin if (bcd_ready) final_bcd = bcd_number; case(ctrl) 0: digit = digits[3:0]; 1: digit = digits[31:4] ? digits[7:4] : 10; 2: digit = digits[31:8] ? digits[11:8] : 10; 3: digit = digits[31:12] ? digits[15:12] : 10; 4: digit = digits[31:16] ? digits[19:16] : 10; 5: digit = digits[31:20] ? digits[23:20] : 10; 6: digit = digits[31:24] ? digits[27:24] : 10; 7: digit = digits[31:28] ? digits[31:28] : 10; endcase delay = delay + 1; if (delay == 10000) ctrl = ctrl + 1; end endmodule
Bcd konvertieren module bcd_convert #(parameter INPUT_WIDTH, parameter DECIMAL_DIGITS) ( input i_Clock, input [INPUT_WIDTH-1:0] i_Binary, input i_Start, output [DECIMAL_DIGITS*4-1:0] o_BCD, output o_DV ); parameter s_IDLE = 3'b000; parameter s_SHIFT = 3'b001; parameter s_CHECK_SHIFT_INDEX = 3'b010; parameter s_ADD = 3'b011; parameter s_CHECK_DIGIT_INDEX = 3'b100; parameter s_BCD_DONE = 3'b101; reg [2:0] r_SM_Main = s_IDLE; // The vector that contains the output BCD reg [DECIMAL_DIGITS*4-1:0] r_BCD = 0; // The vector that contains the input binary value being shifted. reg [INPUT_WIDTH-1:0] r_Binary = 0; // Keeps track of which Decimal Digit we are indexing reg [DECIMAL_DIGITS-1:0] r_Digit_Index = 0; // Keeps track of which loop iteration we are on. // Number of loops performed = INPUT_WIDTH reg [7:0] r_Loop_Count = 0; wire [3:0] w_BCD_Digit; reg r_DV = 1'b0; always @(posedge i_Clock) begin case (r_SM_Main) // Stay in this state until i_Start comes along s_IDLE : begin r_DV <= 1'b0; if (i_Start == 1'b1) begin r_Binary <= i_Binary; r_SM_Main <= s_SHIFT; r_BCD <= 0; end else r_SM_Main <= s_IDLE; end // Always shift the BCD Vector until we have shifted all bits through // Shift the most significant bit of r_Binary into r_BCD lowest bit. s_SHIFT : begin r_BCD <= r_BCD << 1; r_BCD[0] <= r_Binary[INPUT_WIDTH-1]; r_Binary <= r_Binary << 1; r_SM_Main <= s_CHECK_SHIFT_INDEX; end // Check if we are done with shifting in r_Binary vector s_CHECK_SHIFT_INDEX : begin if (r_Loop_Count == INPUT_WIDTH-1) begin r_Loop_Count <= 0; r_SM_Main <= s_BCD_DONE; end else begin r_Loop_Count <= r_Loop_Count + 1; r_SM_Main <= s_ADD; end end // Break down each BCD Digit individually. Check them one-by-one to // see if they are greater than 4. If they are, increment by 3. // Put the result back into r_BCD Vector. s_ADD : begin if (w_BCD_Digit > 4) begin r_BCD[(r_Digit_Index*4)+:4] <= w_BCD_Digit + 3; end r_SM_Main <= s_CHECK_DIGIT_INDEX; end // Check if we are done incrementing all of the BCD Digits s_CHECK_DIGIT_INDEX : begin if (r_Digit_Index == DECIMAL_DIGITS-1) begin r_Digit_Index <= 0; r_SM_Main <= s_SHIFT; end else begin r_Digit_Index <= r_Digit_Index + 1; r_SM_Main <= s_ADD; end end s_BCD_DONE : begin r_DV <= 1'b1; r_SM_Main <= s_IDLE; end default : r_SM_Main <= s_IDLE; endcase end // always @ (posedge i_Clock) assign w_BCD_Digit = r_BCD[r_Digit_Index*4 +: 4]; assign o_BCD = r_BCD; assign o_DV = r_DV; endmodule // Binary_to_BCD
Autoren: Tyurin Leonid, Tikhonov Nikita.