Zusammenführungssorten arbeiten nach diesem Prinzip:

1. Geordnete Subarrays werden durchsucht (optional - gebildet).
2. Geordnete Subarrays werden zu einem gemeinsamen geordneten Subarray verkettet.

Ein geordnetes Subarray innerhalb des Arrays hat für sich genommen nicht viel Wert. Wenn wir jedoch in einem Array zwei geordnete Subarrays finden, ist dies eine völlig andere Sache. Tatsache ist, dass Sie sie sehr schnell und zu minimalen Kosten zusammenführen können - um aus einem Paar geordneter Subarrays ein allgemein geordnetes Subarray zu bilden.



Wie Sie sehen können, ist das Kombinieren von zwei geordneten Arrays zu einem nicht einfach, aber sehr einfach. Sie müssen sich in beiden Arrays gleichzeitig von links nach rechts bewegen und die nächsten Elementpaare aus beiden Arrays vergleichen. Das kleinere Element wird zum gemeinsamen Kessel geschickt. Wenn die Elemente in einem der Arrays enden, werden die verbleibenden Elemente aus dem anderen Array einfach der Reihe nach in die Hauptliste übertragen.

Dies ist das Salz der Algorithmen dieser Klasse. Anfänglich kann ein zufälliges Array in viele kleine geordnete Subarrays unterteilt werden. Beim paarweisen Zusammenführen nimmt die Anzahl der geordneten Subarrays ab, und die Länge jedes einzelnen nimmt zu. Im letzten Schritt besteht das Array nur aus zwei geordneten Subarrays, die zu einer einzigen geordneten Struktur zusammengeführt werden.


Der Autor dieses Konzepts ist John von Neumann. Manchmal gibt es eine kontroverse Behauptung, dass er während der Arbeit am Manhattan-Projekt auf das Sortieren gekommen sei, weil er vor der Aufgabe stand, eine große Menge statistischer Daten bei der Entwicklung einer Atombombe effektiv zu berechnen. Es ist schwierig, die Glaubwürdigkeit dieser Version zu beurteilen, da seine ersten Arbeiten zur Sortierung nach Fusionen aus dem Jahr 1948 stammen und die Erstellung der Bombe drei Jahre zuvor abgeschlossen wurde. Was für eine atomare Sortierung gibt es jedoch? Schauen wir uns das an.

Natürliche Neumann-Fusion

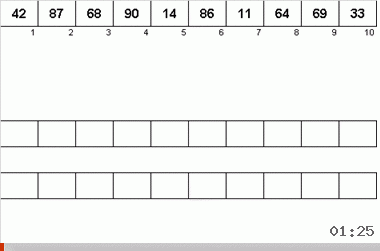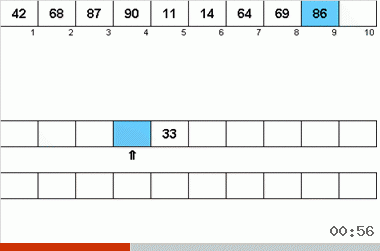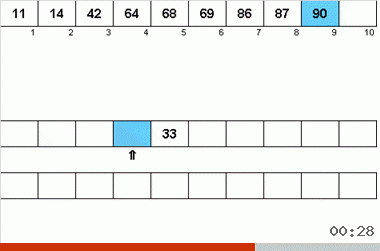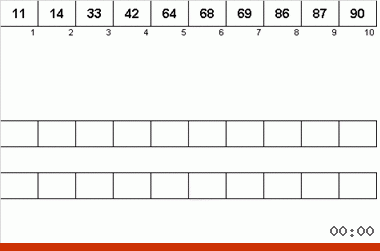
Der Neyman-Algorithmus wurde von den Konstruktionsmerkmalen der Computer der 40er Jahre beeinflusst. Es sah so aus:

1. Insgesamt werden drei Magnetbänder verwendet - das Hauptband, auf dem unsortierte Daten und zwei Hilfsdaten aufgezeichnet werden.
2. Die Daten werden nacheinander vom Hauptband gelesen.
3. Während sequentiell gelesene Daten ein geordnetes Subarray sind, werden sie auf eines der Hilfsbänder kopiert.
4. Sobald das nächste sortierte Subarray fertig ist (d. H. Ein Element, das kleiner als das vorherige ist, befindet sich auf dem Hauptband), wird ein Zeiger auf das Hilfsband (Ende des Subarrays) gesetzt und es erfolgt ein Wechsel zu einem anderen Hilfsband.
5. Die Punkte 2 bis 4 werden erneut wiederholt, nur die Daten werden auf ein anderes Hilfsband übertragen. Am Ende des nächsten bestellten Subarrays wechselt das Hauptband abwechselnd zu einem Hilfsband und dann zu einem anderen.
6. Wenn alle Daten vom Hauptband gelesen wurden, erfolgt die Verarbeitung der Hilfsbänder.
7. Beide Hilfsbänder lesen nacheinander Daten.
8. In diesem Fall werden die nächsten Daten von zwei Bändern miteinander verglichen. Entsprechend den Vergleichsergebnissen wird das kleinste Element des Paares auf dem Hauptband aufgezeichnet.
9. Da die Grenzen von Arrays auf Hilfsbändern mit Zeigern markiert sind, erfolgt das Lesen und Vergleichen nur innerhalb der Grenzen sortierter Subarrays.
10. Wenn auf einem der Hilfsbänder die Elemente des nächsten Subarrays beendet sind, wird der Rest des Subarrays vom verbleibenden Band einfach auf das Hauptband übertragen.
11. Wir wiederholen den gesamten Vorgang erneut, bis die Daten auf dem Hauptband ein vollständig geordnetes Array sind.

Die Neumann-Sortierung ist ein adaptiver Algorithmus: Sie fixiert nicht nur die sortierten Teile des Arrays, sondern versucht auch zunächst, sie zu vergrößern, so dass auf der Basis länglicher geordneter Subarrays noch länger geordnete Subarrays entstehen. Daher wird es auch als adaptive Zusammenführungssortierung bezeichnet .

Die Komplexität dieses Algorithmus ist bescheiden - O ( n ² ), und dennoch war dies für die Pioniere des Röhrencomputers ein Durchbruch.

Am Beispiel dieser ersten Zusammenführungssortierung ist bereits ein Nachteil dieser Klasse von Algorithmen sichtbar - die Kosten für zusätzlichen Speicher. In dieser Hinsicht erfordern fast alle Zusammenführungssortierungen zusätzlich O ( n ), elegante Ausnahmen sind jedoch selten.

Direkte Fusion von Bowes und Nelson

Genau genommen ist der Bowes-Nelson-Algorithmus ein Sortiernetzwerk, keine Sortierung. Dabei werden das Array und alle seine Subarrays in zwei Hälften geteilt, und nichts hindert alle diese Hälften daran, in allen Phasen parallel verarbeitet zu werden. Es kann jedoch auch in Form einer Sortierung dargestellt werden. Und wir kommen auch zum Thema Sortieren von Netzwerken.

1. Das Array ist in zwei Hälften unterteilt - in die linke und rechte Hälfte.
2. Elemente sind in Gruppen unterteilt.
3. Bei der ersten Iteration sind dies die beiden Elemente (das 1. Element der linken Hälfte + das 1. Element der rechten Hälfte, das 2. Element der linken Hälfte + das 2. Element der rechten Hälfte usw.), bei der zweiten Iteration die vier Elemente (1- 2. und 2. Element der linken Hälfte + 1. und 2. Element der rechten Hälfte, 3. und 4. Element der linken Hälfte + 3. und 4. Element der rechten Hälfte usw.), auf der dritten - Acht usw.
4. Elemente jeder Gruppe aus der linken Hälfte sind sortierte Subarrays, Elemente jeder Gruppe aus der rechten Hälfte sind ebenfalls sortierte Subarrays.
5. Führen Sie die sortierten Subarrays aus dem vorherigen Absatz zusammen.
6. Wir kehren zu Punkt 1 zurück. Der Zyklus wird fortgesetzt, bis die Größen der Gruppen kleiner als die Größe des Arrays sind.

Es scheint, dass hier zusätzlicher Speicher benötigt wird. Aber nein! Für eine verständlichere Wahrnehmung in der Animation befinden sich die linke und die rechte Hälfte des Arrays aufeinander, so dass die relative Position der verglichenen Subarrays offensichtlicher ist. Aufgrund der strengen Halbierung ist jedoch ein Algorithmus möglich, bei dem alle Vergleiche und Austausche durchgeführt werden, ohne dass zusätzliche Ressourcen aus dem Speicher erforderlich sind. Was für die Zusammenführungssortierung sehr ungewöhnlich ist.

def bose_nelson(data): m = 1 while m < len(data): j = 0 while j + m < len(data): bose_nelson_merge(j, m, m) j = j + m + m m = m + m return data def bose_nelson_merge(j, r, m): if j + r < len(data): if m == 1: if data[j] > data[j + r]: data[j], data[j + r] = data[j + r], data[j] else: m = m // 2 bose_nelson_merge(j, r, m) if j + r + m < len(data): bose_nelson_merge(j + m, r, m) bose_nelson_merge(j + m, r - m, m) return data 

Es gibt etwas in allen Sortierzusammenführungen, das sie der Wasserstoffbombe ähnlich macht. Zuerst erfolgt die Teilung, dann die Synthese.

Referenzen

Zusammenführen / Zusammenführen

Serienartikel:

• Excel-Anwendung AlgoLab.xlsm
• Sorte austauschen
• Insertion Sorts
• Nach Auswahl sortieren
• Sortierungen zusammenführen
  • Ausgewogene Top-Down- und Bottom-Up-Fusion
  • Mehrphasige Zusammenführungssortierung
  • Kaskadierende Zusammenführungssortierung
  • Oszillierende Zusammenführungssortierung
  • Gewindesortierungen und nicht mischbare Sortierungen
  • Sortiervergleich zusammenführen
• Nach Verteilung sortieren
• Hybridsortierung

Beide im heutigen Artikel erwähnten Sortierungen sind jetzt in der AlgoLab-Anwendung verfügbar (für diejenigen, die Algorithmen mit dieser Excel-Anwendung studieren, aktualisieren Sie die Datei). Und in nur wenigen Tagen, mit der Veröffentlichung einer bevorstehenden Fortsetzung von Merge Sortes, werden mehrere weitere Algorithmen dieser Klasse verfügbar sein.

Es gibt eine Einschränkung für die Bowes-Nelson-Sortierung - die Größe des Arrays muss eine Zweierpotenz sein. Wenn diese Bedingung nicht erfüllt ist, schneidet das Makro das Array auf eine geeignete Größe zu.

Dieser Artikel wurde mit Unterstützung von EDISON Software verfasst, einem Unternehmen, das 3D-Rekonstruktionssoftware schreibt und hochentwickelte Messgeräte entwickelt .