Nach dem wirklichen Boom der Brettspiele Ende der 00er Jahre hinterließ die Familie mehrere Kisten mit Spielen. Eines davon ist das Spiel „Hare and Hedgehog“ in der deutschen Originalversion. Ein Spiel für mehrere Spieler, bei dem das Element der Zufälligkeit minimiert wird und die nüchterne Berechnung und die Fähigkeit des Spielers, in mehreren Schritten nach vorne zu schauen, gewinnt.
Meine häufigen Niederlagen im Spiel führten dazu, dass ich Computer-Intelligenz schrieb, um den besten Zug zu wählen. Intelligenz, idealerweise in der Lage, den Großmeister des Hasen und des Igels zu bekämpfen (und was, Tee, nicht Schach, das Spiel wird einfacher sein). Der Rest des Artikels beschreibt den Entwicklungsprozess, die KI-Logik und einen Link zur Quelle.
Spielregeln Hase und Igel
Auf dem Spielfeld von 65 Zellen gibt es mehrere Spielerchips von 2 bis 6 Teilnehmern (meine Zeichnung, nicht kanonisch, sieht natürlich so lala aus):
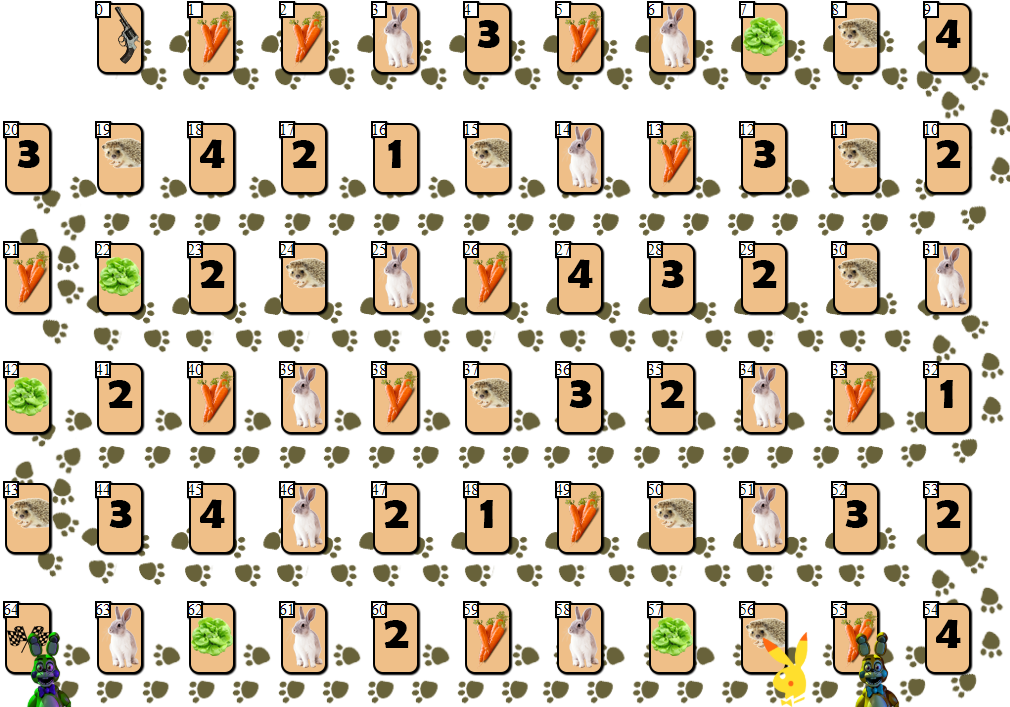
Abgesehen von den Zellen mit den Indizes 0 (Start) und 64 (Ende) kann in jeder Zelle nur ein Spieler platziert werden. Das Ziel eines jeden Spielers ist es, vor den Rivalen in die Zielzelle vorzudringen.
"Treibstoff" für die Weiterentwicklung ist Karotte - die "
Währung " des Spiels. Zu Beginn erhält jeder Spieler 68 Karotten, die er gibt (und manchmal erhält), wenn er sich bewegt.
Zusätzlich zu den Karotten erhält der Spieler zu Beginn 3 Salatkarten. Salat ist ein spezielles „Artefakt“, das ein Spieler vor dem Ziel
loswerden muss. Salat loswerden (und das kann nur mit einem speziellen Salatkäfig gemacht werden, wie folgt:

) erhält der Spieler einschließlich zusätzliche Karotten. Vorher überspringen Sie Ihren Zug. Je mehr Spieler vor dem Salat die Karte verlassen, desto mehr Karotten erhält der Spieler: 10 x (die Position des Spielers auf dem Spielfeld im Verhältnis zu anderen Spielern). Das heißt, der Spieler, der als Zweiter auf dem Feld steht, erhält 20 Karotten und verlässt den Käfig des Salats.
Zellen mit den Nummern 1 bis 4 können mehrere zehn Karotten bringen, wenn die Position des Spielers mit der Nummer auf der Zelle übereinstimmt (1 bis 4, die Zelle mit der Nummer 1 ist auch für die 4. und 6. Position auf dem Spielfeld geeignet), analog zur Salatzelle.
Der Spieler kann den Zug überspringen, mit dem Bild der Karotten auf dem Käfig bleiben und 10 Karotten für diese Aktion erhalten oder geben. Warum sollte ein Spieler "Treibstoff" geben? Tatsache ist, dass ein Spieler nach seinem letzten Zug nur noch 10 Karotten haben kann (20, wenn Sie Zweiter werden, 30, wenn Sie Dritter werden usw.).
Schließlich kann der Spieler 10 x N Karotten erhalten, indem er N Schritte auf dem
nächsten freien Igel macht (wenn der nächste Igel beschäftigt ist, ist eine solche Bewegung unmöglich).
Die Kosten für die Weiterentwicklung werden nicht proportional zur Anzahl der Umzüge gemäß der Formel (mit Aufrundung) berechnet:
,
Dabei ist N die Anzahl der Schritte vorwärts.
Um eine Zelle vorwärts zu bringen, gibt der Spieler 1 Karotte, 3 Karotten für 2 Zellen, 6 Karotten für 3 Zellen, 10 für 4, ..., 210 Karotten, um 20 Zellen vorwärts zu bewegen.
Die letzte Zelle - die Zelle mit dem Bild eines Hasen - bringt ein zufälliges Element in das Spiel. Nachdem der Spieler mit einem Hasen auf einem Käfig gestanden hat, zieht er eine spezielle Karte vom Stapel, woraufhin eine Aktion ausgeführt wird. Abhängig von der Karte und der Spielsituation kann der Spieler einige Karotten verlieren, zusätzliche Karotten erhalten oder eine Runde überspringen. Es ist erwähnenswert, dass es unter den Karten mit „Effekten“ mehrere weitere negative Szenarien für den Spieler gibt, die das Spiel dazu ermutigen, vorsichtig und kalkuliert zu sein.
Implementierung ohne KI
In der allerersten Implementierung, die dann die Grundlage für die Entwicklung des Spiels „Intellekt“ bilden wird, habe ich mich auf die Option beschränkt, bei der jeder Spieler einen Zug macht - eine Person.
Ich habe beschlossen, das Spiel als Client zu implementieren - eine statische einseitige Website, deren „Logik“ auf dem JS und dem Server implementiert ist - der WEB-API-Anwendung. Der Server ist in .NET Core 2.1 geschrieben und erzeugt ein Assembly-Artefakt - eine DLL-Datei, die unter Windows / Linux / Mac OS ausgeführt werden kann.
Die „Logik“ des Client-Teils wird minimiert (ebenso wie die UX, da die GUI rein zweckmäßig ist). Beispielsweise führt der Webclient die Überprüfung selbst nicht durch, um festzustellen, ob die vom Spieler angeforderten Regeln akzeptabel sind. Diese Prüfung wird auf dem Server durchgeführt. Der Server teilt dem Client mit, welche Bewegungen der Spieler von der aktuellen Spielposition aus ausführen kann.
Der Server ist eine klassische
Moore-Maschine . In der Serverlogik fehlen Konzepte wie "verbundener Client", "Spielsitzung" usw.
Der Server verarbeitet lediglich den empfangenen Befehl (HTTP POST). Das
Befehlsmuster ist auf dem Server implementiert. Der Client kann die Ausführung eines der folgenden Befehle anfordern:
- ein neues Spiel starten, d.h. Legen Sie Chips der angegebenen Anzahl von Spielern auf ein "sauberes" Brett
- Führen Sie die im Befehl angegebene Bewegung aus
Für das zweite Team sendet der Client dem Server die aktuelle Spielposition (Objekt der Disposition-Klasse), d. H. Eine Beschreibung der folgenden Form:
- Position, Anzahl der Karotten und Salat für jeden Hasen sowie ein zusätzliches Boolesches Feld, das anzeigt, dass der Hase nicht an der Reihe ist
- Index des Hasen, der sich bewegt.
Der Server muss keine zusätzlichen Informationen senden, z. B. Informationen zum Spielfeld. Genau wie beim Aufzeichnen einer Schachskizze ist es nicht erforderlich, die Anordnung der schwarzen und weißen Zellen auf die Tafel zu malen - diese Information wird als Konstante genommen.
Als Antwort zeigt der Server an, ob der Befehl erfolgreich ausgeführt wurde. Technisch kann ein Client beispielsweise einen ungültigen Umzug anfordern. Oder versuchen Sie, ein neues Spiel für einen einzelnen Teilnehmer zu erstellen, was offensichtlich keinen Sinn ergibt.
Wenn das Team erfolgreich ist, enthält die Antwort eine neue
Spielposition sowie eine Liste der Züge, die der nächste Spieler in der Warteschlange ausführen kann (aktuell für die neue Position).
Darüber hinaus enthält die Serverantwort einige Servicefelder. Zum Beispiel der Text einer Karte eines Hasen, der von einem Spieler bei einem Schritt auf dem entsprechenden Käfig „herausgezogen“ wurde.
Spieler an der Reihe
Der Zug des Spielers wird als Ganzzahl codiert:
- 0, wenn der Spieler gezwungen ist, in der aktuellen Zelle zu bleiben,
1, 2, ... N für 1, ... N tritt vor, - -1, -2, ... -M, um 1 ... M Zellen zurück zum nächsten freien Igel zu bewegen,
- 1001, 1002 - spezielle Codes für den Spieler, der sich entschieden hat, in der Karottenzelle zu bleiben und dafür 10 Karotten zu erhalten (1001) oder zu geben (1002).
Software-Implementierung
Der Server empfängt den JSON des angeforderten Befehls, analysiert ihn in eine der entsprechenden Anforderungsklassen und führt die angeforderte Aktion aus.
Wenn der Client (Spieler) von der an das Team übertragenen Position (POS) einen Zug mit dem CMD-Code anfordert, führt der Server die folgenden Aktionen aus:
- prüft, ob ein solcher Umzug möglich ist
- erstellt eine neue Position aus der aktuellen und nimmt entsprechende Änderungen daran vor,
bekommt viele mögliche Züge für eine neue Position. Ich möchte Sie daran erinnern, dass der Index des Spielers, der den Zug ausführt, bereits in dem Objekt enthalten ist, das die Position beschreibt. - gibt dem Kunden eine Antwort mit einer neuen Position, möglichen Bewegungen oder dem Erfolgsflag gleich false und einer Beschreibung des Fehlers zurück.
Die Logik, die Zulässigkeit des angeforderten Umzugs (CMD) zu überprüfen und eine neue Position zu konstruieren, erwies sich als etwas enger miteinander verbunden, als wir es gerne hätten. Mit dieser Logik hat die Methode, akzeptable Bewegungen zu finden, etwas gemeinsam. All diese Funktionen werden von der TurnChecker-Klasse implementiert.
Bei der Eingabe der Check / Execute-Methoden erhält TurnChecker ein Objekt der Klasse der Spielposition (Disposition). Das Disposition-Objekt enthält ein Array mit Spielerdaten (Haze [] hazes), dem Index des Spielers, der den Zug ausführt, sowie einigen Serviceinformationen, die während des Betriebs des TurnChecker-Objekts eingegeben wurden.
Das Spielfeld beschreibt die FieldMap-Klasse, die als
Singleton implementiert ist. Die Klasse enthält ein Array von Zellen + einige Overhead-Informationen, die zur Vereinfachung / Beschleunigung nachfolgender Berechnungen verwendet werden.
LeistungsüberlegungenBei der Implementierung der TurnChecker-Klasse habe ich versucht, Schleifen so weit wie möglich zu vermeiden. Tatsache ist, dass Verfahren zum Erhalten des Satzes zulässiger Bewegungen / Ausführung einer Bewegung anschließend während des Suchvorgangs für eine quasi optimale Bewegung Tausende (Zehntausende) Mal aufgerufen werden.
So berechne ich zum Beispiel anhand der folgenden Formel, wie viele Zellen ein Spieler mit N Karotten vorwärts bringen kann:
return ((int)Math.Pow(8 * N + 1, 0.5) - 1) / 2;
Wenn ich überprüfe, ob Zelle i von einem der Spieler besetzt ist, gehe ich nicht die Liste der Spieler durch (da diese Aktion wahrscheinlich viele Male ausgeführt werden muss), sondern wende mich dem Wörterbuch der Form
[cell_index, Busy_cage_ Flag] zu, das im Voraus ausgefüllt wurde.
Bei der Überprüfung, ob die angegebene
Igelzelle der aktuellen Zelle, die der Spieler belegt, am nächsten (dahinter) liegt, vergleiche ich auch die angeforderte Position mit einem Wert aus einem Wörterbuch der Form
[cell_index, next_back_dezh] _index] - statische Informationen.
Implementierung mit AI
Der Liste der vom Server verarbeiteten Befehle wird ein Befehl hinzugefügt: Führen Sie eine vom Programm ausgewählte quasi-optimale Bewegung aus. Dieses Team ist eine kleine Modifikation des Befehls "Spieler bewegen", aus dem das Bewegungsfeld (
CMD ) entfernt wurde.
Die erste Entscheidung, die mir in den Sinn kommt, ist die Verwendung von Heuristiken, um den „bestmöglichen“ Zug auszuwählen. In Analogie zum Schach können wir jede der mit unserem Zug erhaltenen Spielpositionen bewerten, indem wir eine Bewertung für diese Position festlegen.
Heuristische Positionsbewertung
Zum Beispiel ist es im Schach ganz einfach, eine Bewertung vorzunehmen (ohne in die Wildnis der Öffnungen zu kriechen): Zumindest können Sie die Gesamtkosten der Figuren berechnen, indem Sie den Ritter- / Bischofswert für 3 Bauern, den Wert eines Turmes auf 5 Bauern, die Königin auf 9 und den König auf
int setzen .MaxValue Bauern. Es ist einfach, die Schätzung zu verbessern, indem Sie sie beispielsweise hinzufügen (mit einem Korrekturfaktor - Faktor / Exponent oder einer anderen Funktion):
- die Anzahl der möglichen Bewegungen von der aktuellen Position,
- Verhältnis von Bedrohungen zu feindlichen Figuren / Bedrohungen durch den Feind.
Die Position der Matte wird speziell bewertet:
int.MaxValue , wenn der Schachmatt den Computer platziert hat,
int.MinValue, wenn der Schachmatt die Person platziert hat.
Wenn Sie dem Schachprozessor befehlen, den nächsten Zug zu wählen, der nur von einer solchen Bewertung geleitet wird, wird der Prozessor wahrscheinlich nicht die schlechtesten Züge wählen. Insbesondere:
- Verpassen Sie nicht die Gelegenheit, ein größeres Stück oder Schachmatt zu nehmen.
- höchstwahrscheinlich wird es die Figuren in den Ecken nicht treiben,
- Die Figur wird nicht erneut angegriffen (angesichts der Anzahl der Bedrohungen in der Bewertung).
Natürlich lassen solche Bewegungen des Computers ihm keine Chance auf Erfolg mit einem Gegner, der seine Bewegungen im geringsten Sinne macht. Der Computer ignoriert alle Stecker. Außerdem zögert er wahrscheinlich nicht, die Königin gegen einen Bauern einzutauschen.
Trotzdem ist der Algorithmus zur heuristischen Bewertung der aktuellen Schachposition im Schach (ohne die Lorbeeren des Champion-Programms zu beanspruchen) ziemlich transparent. Über das Spiel Hare and Hedgehog kann man nichts sagen.
Im allgemeinen Fall funktioniert im Spiel Hase und Igel eine eher verschwommene Maxime: „
Es ist besser, mit mehr Karotten und weniger Salat weiter zu gehen “. Allerdings ist nicht alles so einfach. Wenn ein Spieler mitten im Spiel 1 Salatkarte hat, kann diese Option recht gut sein. Aber der Spieler, der mit einer Salatkarte an der Ziellinie steht, ist offensichtlich in einer Verlustsituation. Neben dem Bewertungsalgorithmus möchte ich auch einen Schritt weiter „gucken“ können, so wie Bedrohungen für Figuren in einer heuristischen Bewertung einer Schachposition gezählt werden können. Zum Beispiel lohnt es sich, den Bonus von Karotten zu berücksichtigen, die ein Spieler erhält, der die Salatzelle / Positionszelle verlässt (1 ... 4), wobei die Anzahl der Spieler vor ihm zu berücksichtigen ist.
Ich habe die Abschlussnote als Funktion abgeleitet:
E = Ks · S + Kc · C + Kp · P,
Dabei sind S, C, P Noten, die mit Salatkarten (S) und Karotten © in den Händen des Spielers berechnet wurden. P sind die Noten, die dem Spieler für die zurückgelegte Strecke gegeben wurden.
Ks, Kc, Kp sind die entsprechenden Korrekturfaktoren (sie werden später diskutiert).
Am einfachsten ist es, die Markierung für
den zurückgelegten Weg zu bestimmen:
P = i * 3, wobei i der Index der Zelle ist, auf der sich der Spieler befindet.
Die Einstufung C (Karotten) ist bereits schwieriger.
Um einen bestimmten C-Wert zu erhalten, wähle ich eine von 3 Funktionen
von einem Argument (die Anzahl der Karotten auf den Händen). Der Index der Funktion C ([0, 1, 2]) wird durch die relative Position des Spielers auf dem Spielfeld bestimmt:
- [0] Wenn der Spieler weniger als die Hälfte des Spielfelds abgeschlossen hat,
- [2] wenn ein Spieler genug (mb, sogar reichlich) Karotten hat, um fertig zu werden,
- [1] in anderen Fällen.
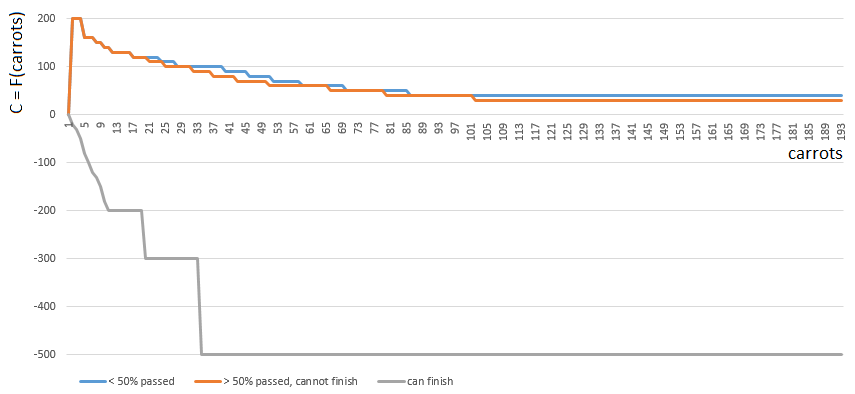
Die Funktionen 0 und 1 sind ähnlich: Der „Wert“ jeder Karotte in den Händen des Spielers nimmt mit zunehmender Anzahl von Karotten in den Händen allmählich ab. Das Spiel ermutigt die Plyushkins selten. Im Fall 1 (die Hälfte des Feldes passiert) nimmt der Wert der Karotten etwas schneller ab.
Funktion 2 (der Spieler kann fertig werden) verhängt im Gegenteil eine hohe Geldstrafe (negativer Koeffizientenwert) gegen jede Karotte in den Händen des Spielers - je mehr Karotten, desto größer der Strafkoeffizient. Da bei einem Überschuss an Karotten das Finish nach den Spielregeln verboten ist.
Vor der Berechnung der Karottenmenge auf den Händen des Spielers wird unter Berücksichtigung der Karotten pro Zug aus der Salatzelle / Zellnummer 1 ... 4 angegeben.
In ähnlicher Weise wird eine „
Salat “ -Sorte S abgeleitet. Abhängig von der Menge an Salat auf den Händen des Spielers (0 ... 3) wird eine Funktion ausgewählt
oder
. Funktionsargument
. - wieder der "relative" Pfad, den der Spieler zurückgelegt hat. Die Anzahl der Zellen, vor denen Salat verbleibt (relativ zu der vom Spieler belegten Zelle):
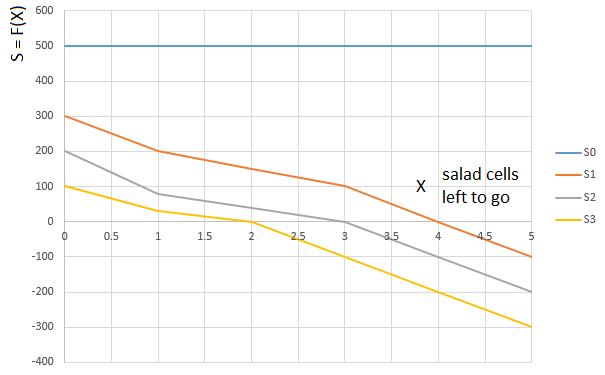
Die Kurve
- Bewertungsfunktion (S) für die Anzahl der Salatzellen vor dem Spieler (0 ... 5) für einen Spieler mit 0 verfügbaren Salatkarten;
die Kurve
- die gleiche Funktion für einen Spieler mit einer Salatkarte usw.
Die Abschlussnote (E = Ks * S + Kc * C + Kp * P) berücksichtigt somit:
- die zusätzliche Menge an Karotten, die der Spieler unmittelbar vor seinem eigenen Zug erhält,
- den Pfad des Spielers
- die Menge an Karotten und Salat auf den Händen, die die Punktzahl nichtlinear beeinflusst.
Und so spielt ein Computer und wählt den nächsten Zug mit der maximalen heuristischen Punktzahl:
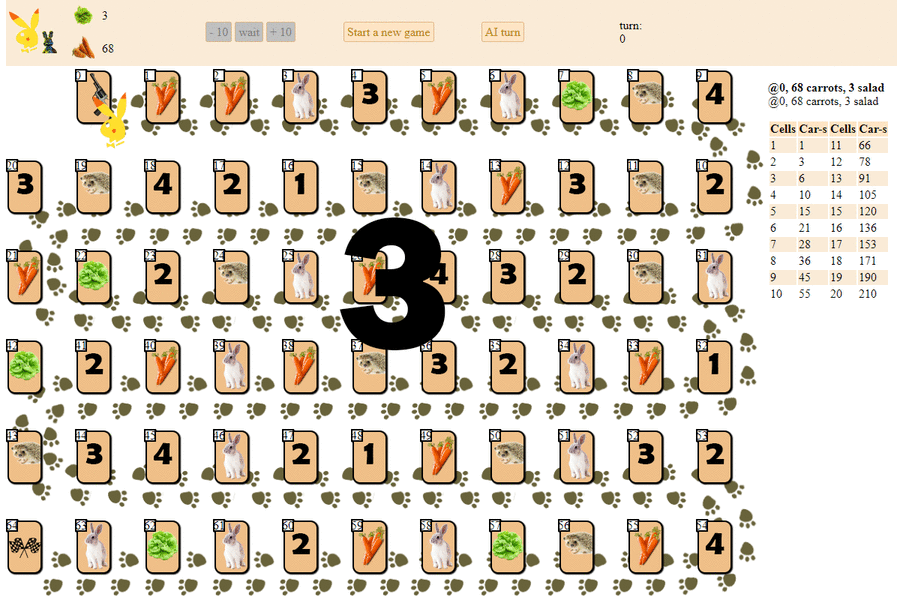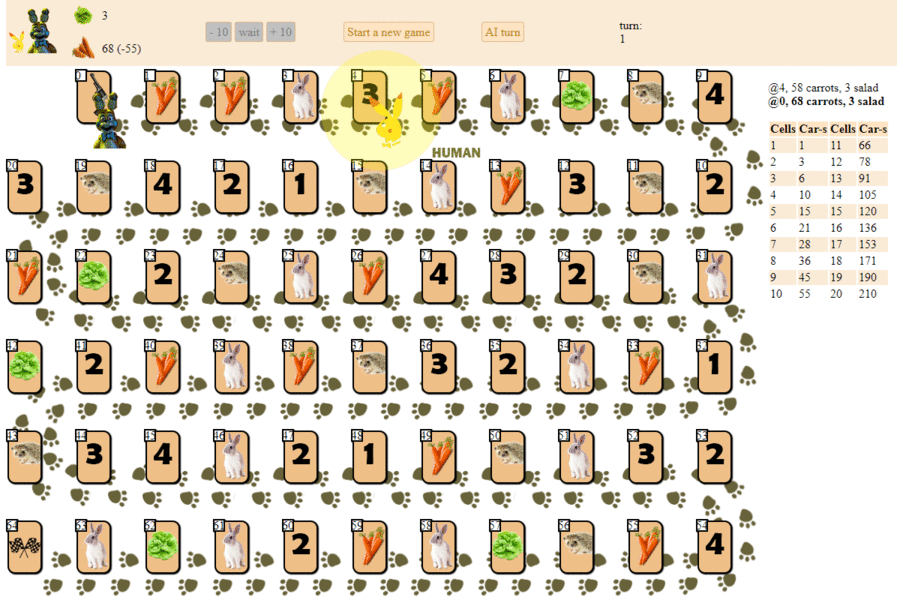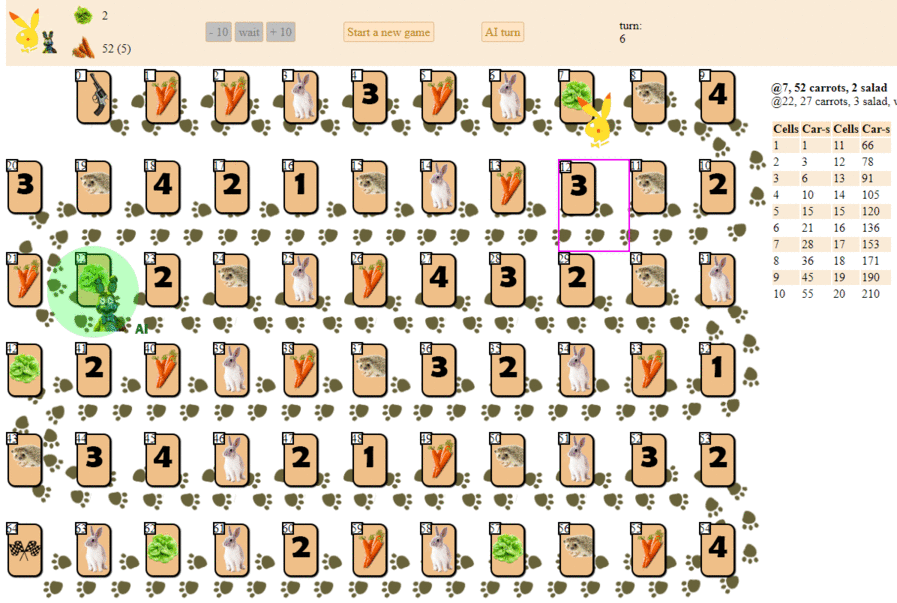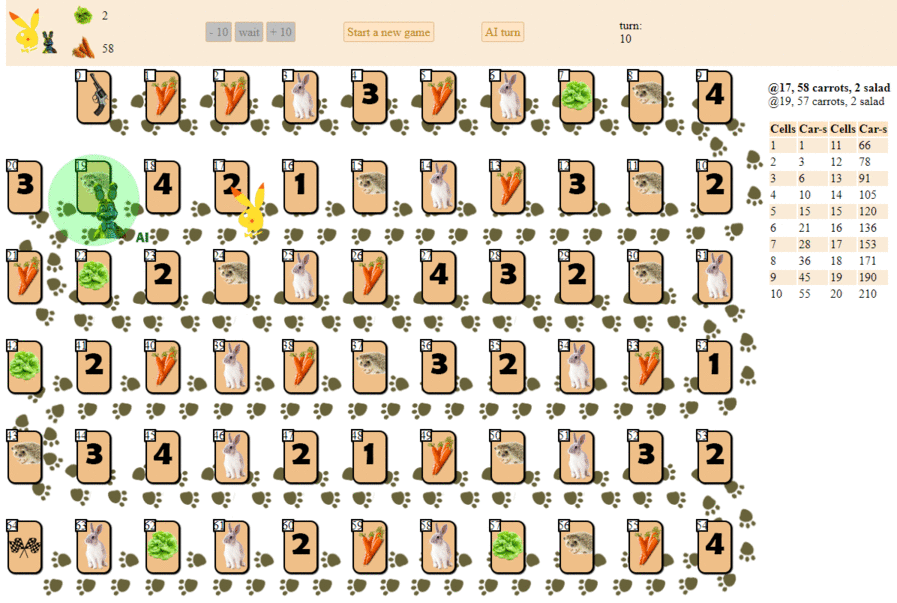
Im Prinzip ist das Debüt nicht so schlecht. Von einer solchen KI sollte man jedoch kein gutes Spiel erwarten: In der Mitte des Spiels beginnt der grüne „Roboter“, wiederholte Bewegungen auszuführen, und am Ende führt er mehrere Iterationen von Bewegungen vorwärts - rückwärts zum Igel durch, bis er schließlich beendet ist. Teilweise zufällig wird er hinter dem Spieler landen - eine Person mit einem Dutzend Zügen.
ImplementierungshinweiseDie Berechnung der Bewertung wird von einer speziellen Klasse verwaltet - EstimationCalculator. Die Funktionen zur Bewertung der Position relativ zu Karottensalatkarten werden im statischen Konstruktor der Rechnerklasse in Arrays geladen. Bei der Eingabe empfängt die Positionsschätzungsmethode das Positionsobjekt selbst und den Index des Spielers, aus dessen „Sicht“ die Position vom Algorithmus bewertet wird. Das heißt, dieselbe Spielposition kann mehrere unterschiedliche Bewertungen erhalten, je nachdem für welchen Spieler die virtuellen Punkte berücksichtigt werden.
Entscheidungsbaum und Minimax-Algorithmus
Wir verwenden den Entscheidungsalgorithmus im antagonistischen Minimax-Spiel. Sehr gut, meiner Meinung nach ist der Algorithmus in
diesem Beitrag beschrieben (Übersetzung) .
Wir bringen dem Programm bei, ein paar Schritte vorauszuschauen. Angenommen, von der aktuellen Position aus (und der Hintergrund ist für den Algorithmus nicht wichtig - wie wir uns erinnern, funktioniert das Programm wie
eine Moore-Maschine ), nummeriert durch die Nummer 1, kann das Programm zwei Züge ausführen. Wir erhalten zwei mögliche Positionen, 2 und 3. Als nächstes ist der Spieler an der Reihe - die Person (im allgemeinen Fall der Feind). Ab der 2. Position hat der Gegner 3 Züge, ab der dritten nur noch zwei Züge. Als nächstes fällt die Runde, um wieder einen Zug zu machen, auf das Programm, das insgesamt 10 Züge von 5 möglichen Positionen machen kann:
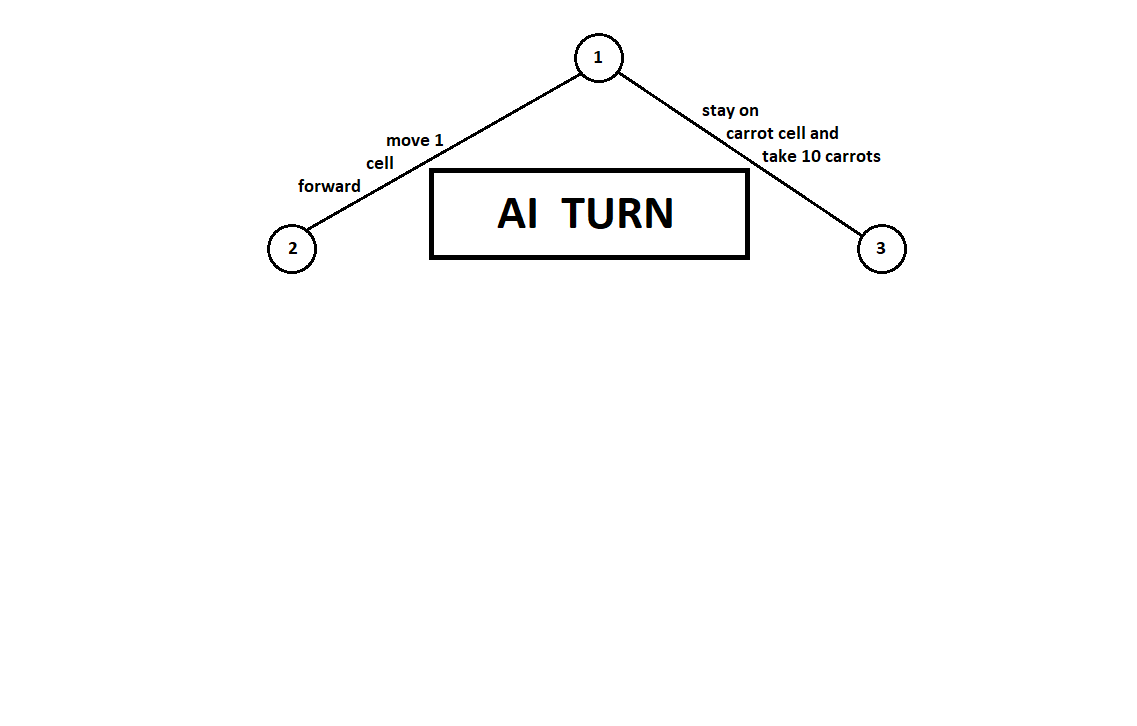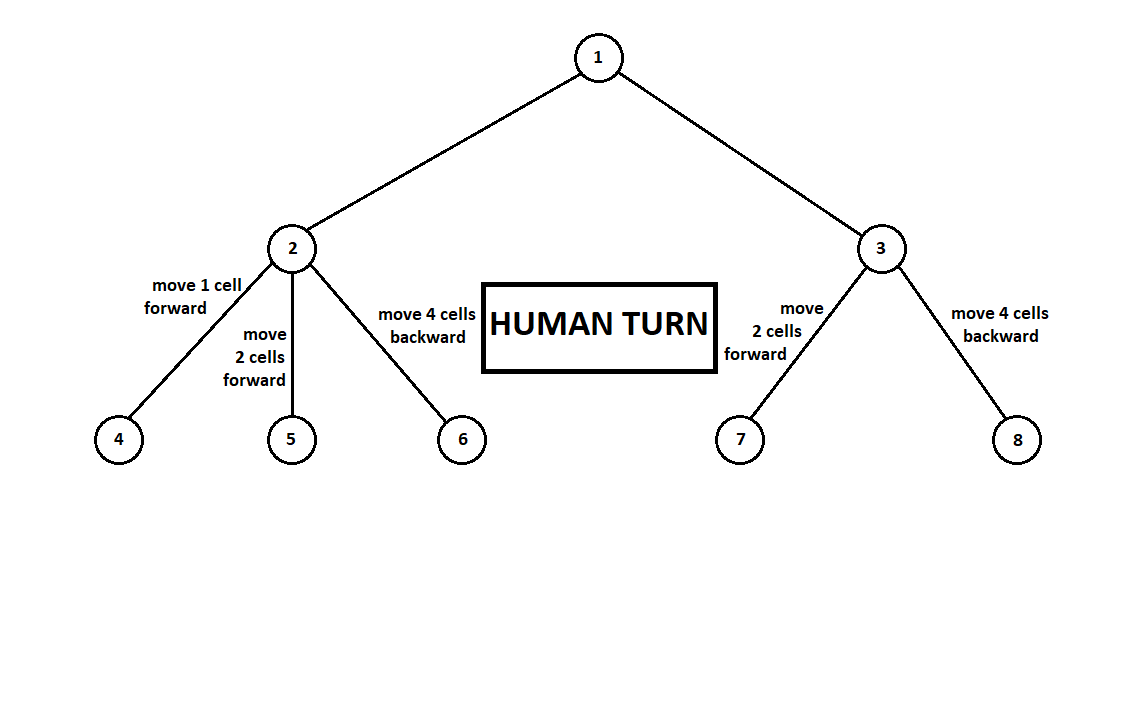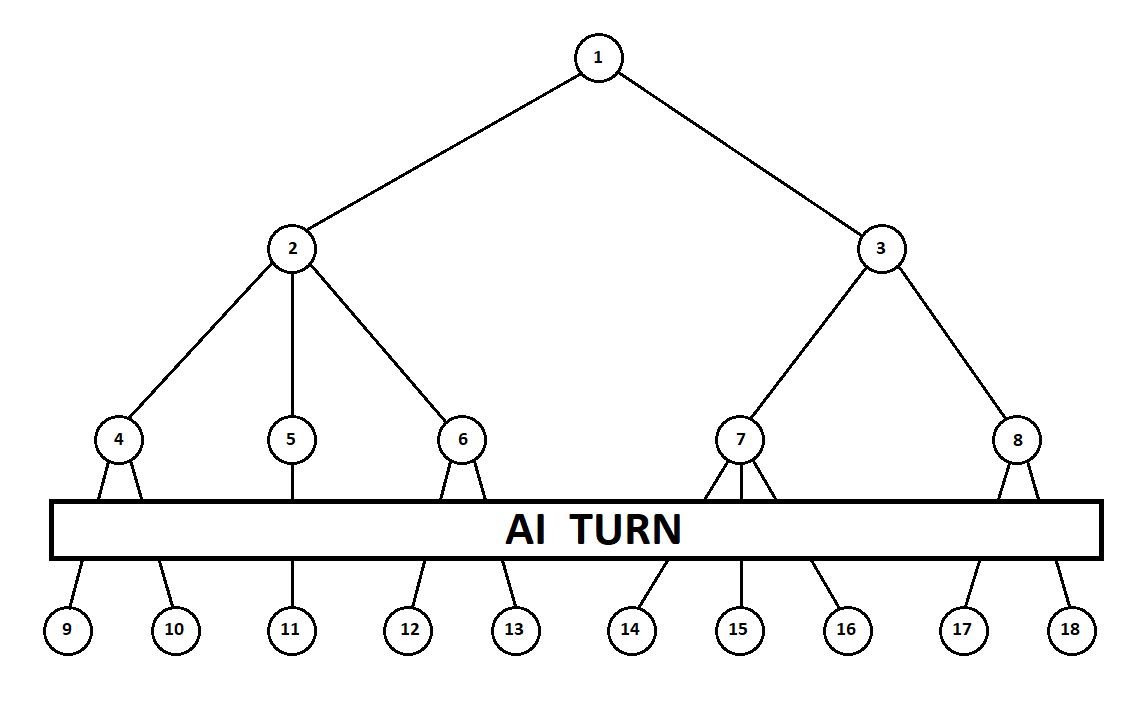
Angenommen, nach dem zweiten Zug des Computers endet das Spiel und jede der empfangenen Positionen wird aus der Sicht des ersten und des zweiten Spielers bewertet. Und wir haben den Bewertungsalgorithmus bereits implementiert. Bewerten wir jede der Endpositionen (Blätter des Baumes 9 ... 18) in Form eines Vektors
,
wo
- Punktzahl berechnet für den ersten Spieler,
- Punktzahl des zweiten Spielers:
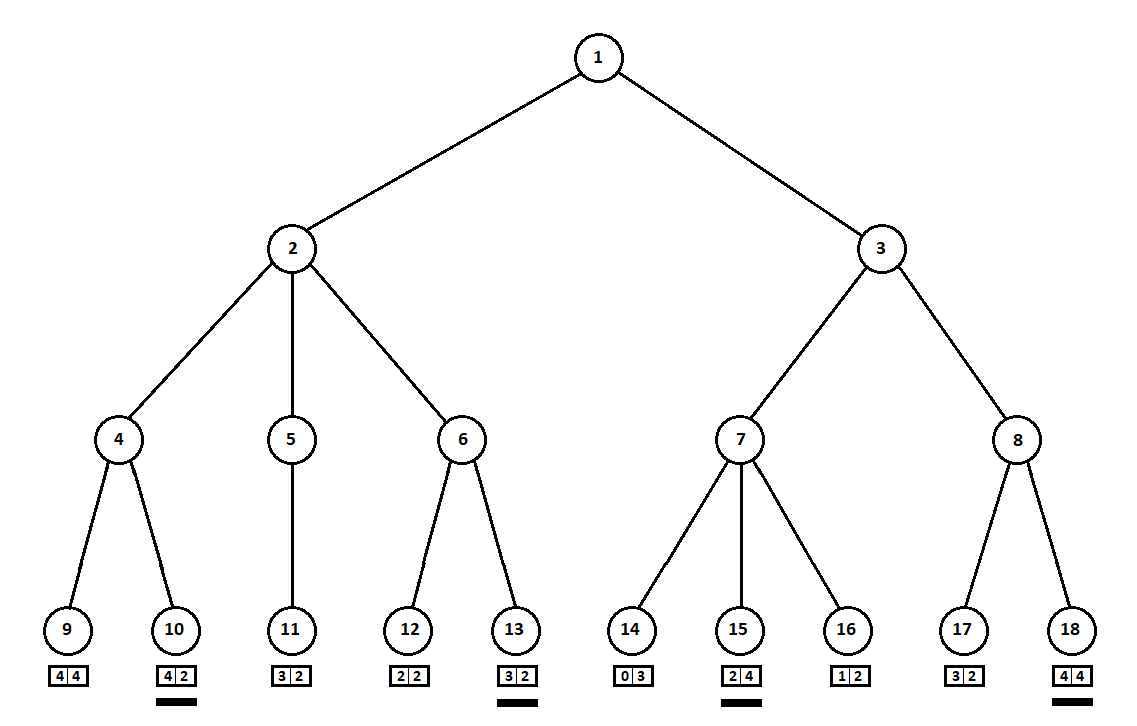
Da der Computer den letzten Schritt macht, wählt er offensichtlich die Optionen in jedem der Teilbäume aus ([9, 10], [11], [12, 13], [14, 15, 16], [17, 18]). das gibt ihm eine bessere Bewertung. Es stellt sich sofort die Frage: Nach welchem Prinzip sollte man die „beste“ Position wählen?
Zum Beispiel gibt es zwei Züge, nach denen wir Positionen mit Ratings haben [5; 5] und [2; 1]. Wertet den ersten Spieler aus. Zwei Alternativen liegen auf der Hand:
- Positionsauswahl mit dem maximalen Absolutwert der i-ten Punktzahl für den i-ten Spieler. Mit anderen Worten, der edle Rennfahrer Leslie, der ohne Rücksicht auf die Konkurrenten den Sieg anstrebt. In diesem Fall ist eine Position mit einer Schätzung von [5; 5].
- Die Wahl einer Position mit der maximalen Bewertung im Verhältnis zu den Schätzungen der Wettbewerber ist der listige Professor Faith, der die Gelegenheit nicht verpasst, dem Feind schmutzige Tricks zuzufügen. Bleiben Sie beispielsweise absichtlich hinter einem Spieler zurück, der von der zweiten Position aus starten möchte. Ein Artikel mit Bewertung [2; 1].
In meiner Software-Implementierung habe ich den Notenauswahlalgorithmus (eine Funktion, die den Notenvektor einem Skalarwert für den i-ten Spieler zuordnet) zu einem benutzerdefinierten Parameter gemacht. Weitere Tests zeigten zu meiner Überraschung die Überlegenheit der ersten Strategie - die Wahl der Position durch den maximalen absoluten Wert
.
Merkmale der Software-ImplementierungWenn die erste Option zur Auswahl der besten Note in den Einstellungen der KI (TurnMaker-Klasse) angegeben ist, hat der Code der entsprechenden Methode die Form:
int ContractEstimateByAbsMax(int[] estimationVector, int playerIndex) { return estimationVector[playerIndex]; }
Die zweite Methode - das Maximum im Verhältnis zu den Positionen der Wettbewerber - ist etwas komplizierter implementiert:
int ContractEstimateByRelativeNumber(int[]eVector, int player) { int? min = null; var pVal = eVector[player]; for (var i = 0; i < eVector.Length; i++) { if (i == player) continue; var val = pVal - eVector[i]; if (!min.HasValue || min.Value > val) min = val; } return min.Value; }
Ausgewählte Schätzungen (in der Abbildung unterstrichen) werden auf die Ebene nach oben übertragen. Jetzt muss der Feind eine Position auswählen und wissen, welche nachfolgende Position der Algorithmus wählen wird:
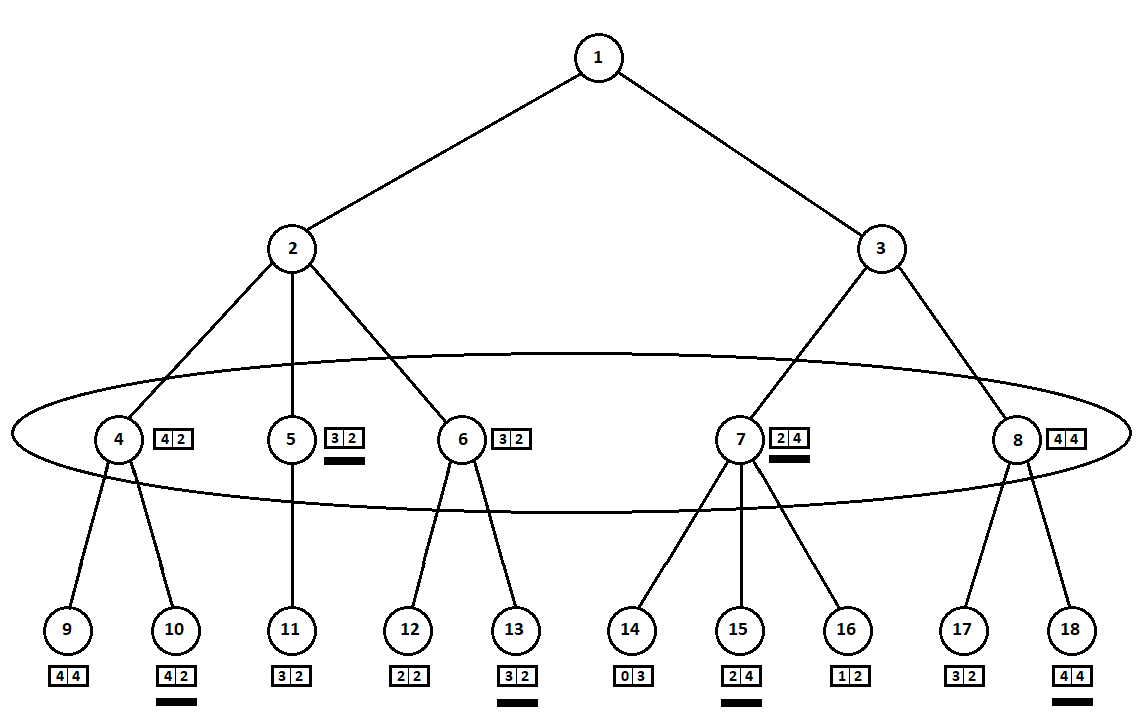
Der Gegner wählt offensichtlich die Position mit der besten Bewertung für sich selbst (diejenige, an der die
zweite Koordinate des Vektors den größten Wert annimmt). Diese Schätzungen sind in der Grafik erneut unterstrichen.
Schließlich kehren wir zum ersten Schritt zurück. Der Computer wählt aus und bevorzugt die Bewegung mit der größten ersten Koordinate des Vektors:
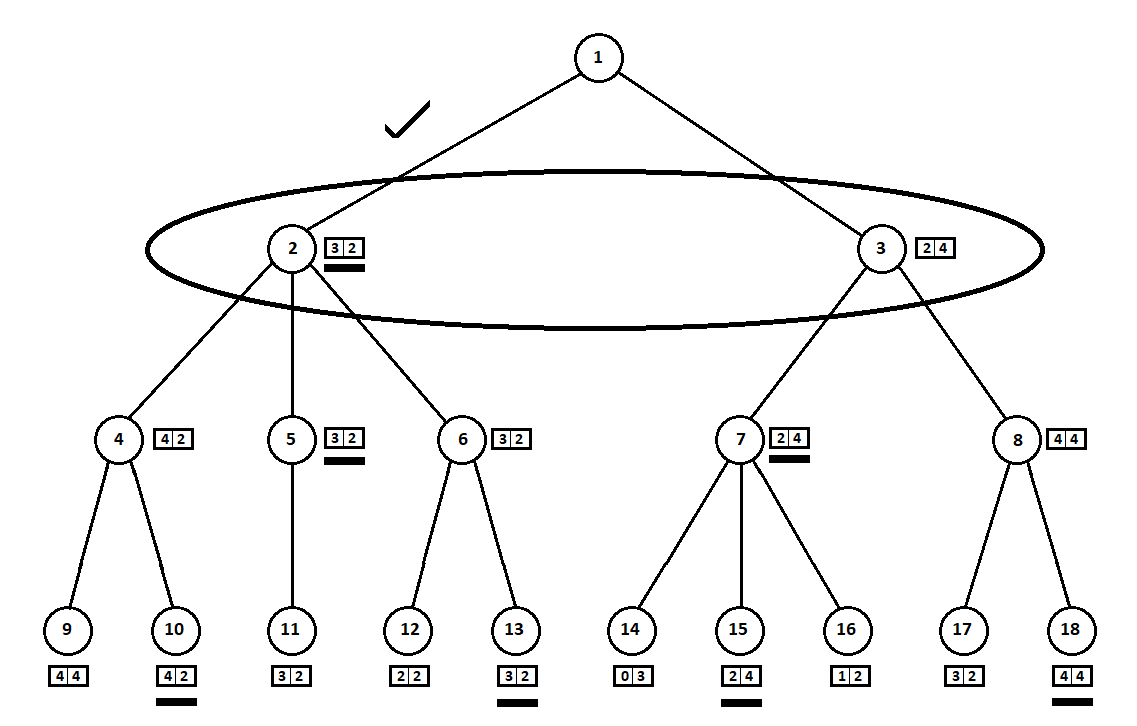
Damit ist das Problem gelöst - es wird ein quasi optimaler Zug gefunden. Angenommen, eine heuristische Bewertung von 100% in Blattpositionen auf einem Baum zeigt einen zukünftigen Gewinner an. Dann wählt unser Algorithmus eindeutig den bestmöglichen Zug.
Die heuristische Punktzahl ist jedoch nur dann 100% genau, wenn die
endgültige Position des Spiels bewertet wurde - ein (oder mehrere) Spieler sind fertig, der Gewinner wird ermittelt. Wenn Sie also die Möglichkeit haben, nach vorne zu schauen, können Sie den optimalen Zug wählen. So viel Zeit erforderlich ist, um Rivalen mit gleicher Stärke zu gewinnen.
Ein typisches Spiel für 2 Spieler dauert durchschnittlich 30 bis 40 Züge (für drei Spieler etwa 60 Züge usw.). Von jeder Position aus kann ein Spieler normalerweise ungefähr 8 Züge machen. Folglich besteht ein vollständiger Baum möglicher Positionen für 30 Züge aus ungefähr
= 1237940039285380274899124224 Spitzen!
In der Praxis dauert das Erstellen und "Parsen" eines Baums mit ~ 100.000 Positionen auf meinem PC ungefähr 300 Millisekunden. Dies gibt uns eine Grenze für die Tiefe des Baums in 7 - 8 Ebenen (Bewegungen), wenn wir eine Computerantwort von nicht mehr als einer Sekunde erwarten möchten.
Merkmale der Software-ImplementierungOffensichtlich ist eine rekursive Methode erforderlich, um einen Baum von Positionen zu erstellen und den besten Zug zu finden. Am Eingang der Methode - die aktuelle Position (an der, wie wir uns erinnern, der Spieler bereits einen Zug macht) und die aktuelle Baumstufe (Zugnummer). Sobald wir auf das von den Algorithmuseinstellungen maximal zulässige Niveau absteigen, gibt die Funktion einen heuristischen Positionsschätzungsvektor aus der Sicht jedes Spielers zurück.
Ein wichtiger Zusatz : Der Abstieg unter dem Baum muss auch gestoppt werden, wenn der aktuelle Spieler fertig ist. Andernfalls (wenn der Algorithmus zur Auswahl der besten Position im Verhältnis zu den Positionen anderer Spieler ausgewählt ist) kann das Programm lange Zeit im Ziel „stampfen“ und den Gegner „verspotten“. Außerdem werden wir auf diese Weise die Größe des Baums im Endspiel geringfügig reduzieren.
Wenn wir uns noch nicht auf der endgültigen Rekursionsstufe befinden, wählen wir die möglichen Züge aus, erstellen für jeden Zug eine neue Position und übergeben sie an den rekursiven Aufruf der aktuellen Methode.
Warum ist Minimax?In der ursprünglichen Interpretation der Spieler sind immer zwei. Das Programm berechnet die Punktzahl ausschließlich aus der Position des ersten Spielers. Dementsprechend sucht der Spieler mit Index 0 bei der Auswahl der „besten“ Position nach einer Position mit einer maximalen Bewertung, der Spieler mit Index 1 nach einer minimalen Bewertung.
In unserem Fall sollte die Bewertung ein Vektor sein, damit jeder der N Spieler sie unter seinem „Gesichtspunkt“ bewerten kann, wenn die Bewertung im Baum steigt.
KI einstellen
Meine Praxis, gegen den Computer zu spielen, hat gezeigt, dass der Algorithmus nicht so schlecht ist, aber den Menschen immer noch unterlegen. Ich habe beschlossen, die KI auf zwei Arten zu verbessern:
- die Konstruktion / Durchquerung des Entscheidungsbaums optimieren,
- Heuristik verbessern.
Minimax-Algorithmusoptimierung
Im obigen Beispiel könnten wir uns weigern, Position 8 zu berücksichtigen und 2 - 3 Eckpunkte des Baums zu "speichern":
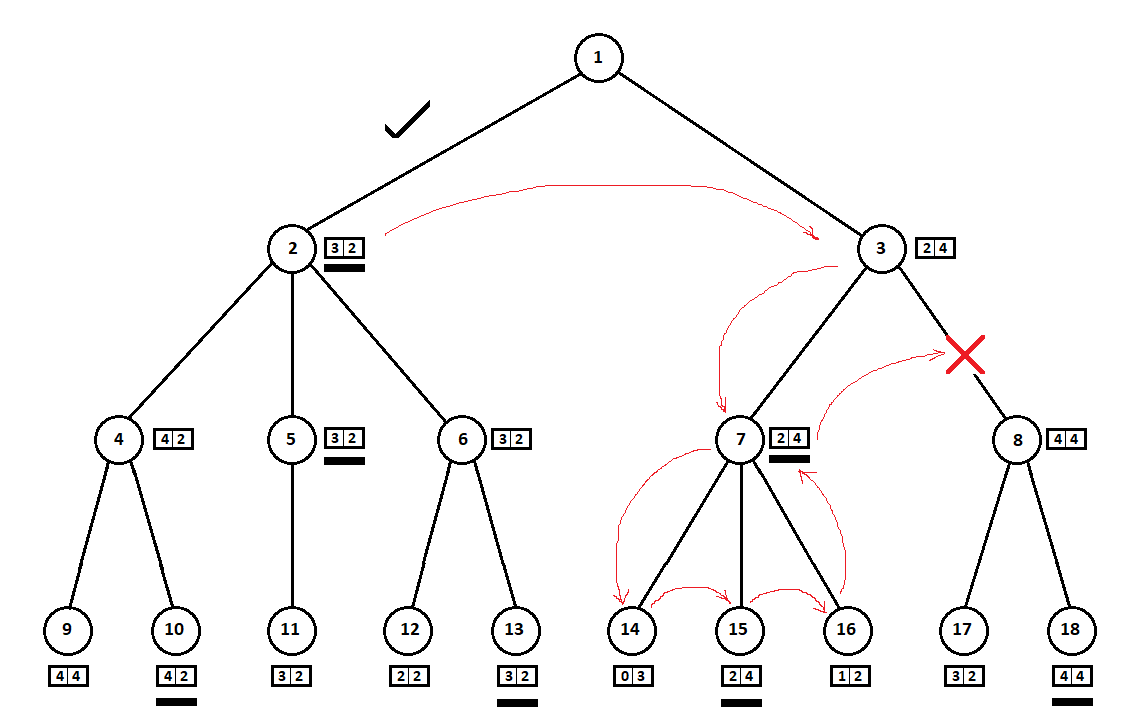
Wir gehen von oben nach unten um den Baum herum, von links nach rechts. Unter Umgehung des Teilbaums ab Position 2 haben wir die beste Schätzung für Zug 1 -> 2 abgeleitet: [3, 2]. Unter Umgehung des Teilbaums mit der Wurzel in Position 7 haben wir die aktuelle Bewertung (am besten für Zug 3 -> 7) ermittelt: [2, 4]. Aus Sicht des Computers (erster Spieler) ist die Punktzahl [2, 4] schlechter als die Punktzahl [3, 2]. Und da der Gegner des Computers unabhängig von der Punktzahl für Position 8 den Zug von Position 3 aus wählt, ist die endgültige Punktzahl für Position 3 a priori schlechter als die Punktzahl für die dritte Position. Dementsprechend kann der Teilbaum mit der Wurzel in Position 8 nicht erstellt und nicht ausgewertet werden.
Die optimierte Version des Minimax-Algorithmus, mit der Sie überschüssige Teilbäume abschneiden können, wird als
Alpha-Beta-Clipping-Algorithmus bezeichnet . Die Implementierung dieses Algorithmus erfordert geringfügige Änderungen am Quellcode.
Merkmale der Software-ImplementierungZwei ganzzahlige Parameter werden zusätzlich an die CalcEstimate-Methode der TurnMaker-Klasse übergeben - alpha, die anfänglich int.MinValue entspricht, und beta, die int.MaxValue entspricht. Ferner wird nach Erhalt einer Schätzung der aktuellen betrachteten Bewegung ein Pseudocode des Formulars ausgeführt:
e = _[0]
Ein wichtiges Merkmal der Software-ImplementierungDie Alpha-Beta-Clipping-Methode führt per Definition zu derselben Lösung wie der „saubere“ Minimax-Algorithmus. Um zu überprüfen, ob sich die Logik der Entscheidungsfindung geändert hat (oder besser gesagt, die Ergebnisse sind Züge), habe ich einen Komponententest geschrieben, bei dem der Roboter 8 Züge für jeden von 2 Gegnern (insgesamt 16 Züge) machte und die resultierende Reihe von Zügen speicherte - mit Clipping-Option deaktiviert .
Dann wurde im gleichen Test der Vorgang mit aktivierter Clipping-Option wiederholt. Danach wurde die Reihenfolge der Bewegungen verglichen. Die Diskrepanz in den Bewegungen zeigt einen Fehler bei der Implementierung des Alpha-Beta-Clipping-Algorithmus an (der Test ist fehlgeschlagen).
Kleinere Optimierung des Alpha-Beta-Clipping
Bei aktivierter Beschneidungsoption in den AI-Einstellungen wurde die Anzahl der Scheitelpunkte im Positionsbaum um das Durchschnitt dreimal reduziert. Dieses Ergebnis kann etwas verbessert werden.
Im obigen Beispiel:

so erfolgreich „zusammenfiel“, dass wir vor dem Teilbaum mit dem Scheitelpunkt in Position 3 den Teilbaum mit dem Scheitelpunkt in Position 2 untersuchten. Wenn die Sequenz anders war, konnten wir mit dem „schlechtesten“ Teilbaum beginnen und nicht zu dem Schluss kommen, dass es keinen Sinn machte, die nächste Position in Betracht zu ziehen .
In der Regel erweist sich das Abschneiden eines Baums als „wirtschaftlicher“. Die untergeordneten Eckpunkte auf derselben Ebene (dh alle möglichen Bewegungen von der i-Position) sind bereits nach der aktuellen Positionsschätzung (ohne tief in die Position zu schauen) sortiert. Mit anderen Worten, wir gehen davon aus, dass der beste Zug (aus heuristischer Sicht) eher eine bessere Abschlussnote erzielt. Daher sortieren wir den Baum mit einiger Wahrscheinlichkeit so, dass der „beste“ Teilbaum vor dem „schlechtesten“ Teil betrachtet wird, wodurch wir mehr Optionen abschneiden können.
Die Beurteilung der aktuellen Position ist ein kostspieliges Verfahren. Wenn es früher ausreichte, nur die Endpositionen (Blätter) zu bewerten, wird jetzt die Bewertung für alle Eckpunkte des Baums vorgenommen. Wie die Tests zeigten, war die Gesamtzahl der vorgenommenen Schätzungen jedoch immer noch etwas geringer als in der Variante ohne die anfängliche Sortierung möglicher Bewegungen.
Merkmale der Software-ImplementierungDer Alpha-Beta-Clipping-Algorithmus gibt den gleichen Zug zurück wie der ursprüngliche Minimax-Algorithmus. Dies überprüft den von uns geschriebenen Komponententest und vergleicht zwei Bewegungssequenzen (für einen Algorithmus mit und ohne Clipping). Alpha-Beta-Clipping mit Sortierung kann im allgemeinen Fall auf eine andere Bewegung als eine quasi optimale hinweisen.
Um den korrekten Betrieb des modifizierten Algorithmus zu testen, benötigen Sie einen neuen Test. Trotz der Modifikation sollte der sortierte Algorithmus genau den gleichen endgültigen Schätzvektor ([3, 2] im Beispiel in der Abbildung) wie der nicht sortierte Algorithmus wie der ursprüngliche Minimax-Algorithmus erzeugen.
Im Test habe ich eine Reihe von Testpositionen erstellt und aus jeder nach der „besten“ Bewegung ausgewählt, wobei die Sortieroption ein- und ausgeschaltet wurde. Dann verglich er den auf zwei Arten erhaltenen Bewertungsvektor.
Da die Positionen für jede der möglichen Bewegungen im aktuellen Scheitelpunkt des Baums durch heuristische Auswertung sortiert sind, schlägt die Idee außerdem vor, einige der schlechtesten Optionen sofort zu verwerfen. Zum Beispiel kann ein Schachspieler einen Zug in Betracht ziehen, bei dem er seinen Turm durch einen Bauerntreffer ersetzt. Wenn er jedoch die Situation in der Tiefe um 3, 4 ... Vorwärtsbewegungen "abrollt", wird er die Optionen sofort bemerken, wenn beispielsweise der Gegner den Bischof seiner Königin angreift.
In den KI-Einstellungen habe ich den Vektor "Abschneiden der schlechtesten Optionen" festgelegt. Zum Beispiel bedeutet ein Vektor der Form [0, 0, 8, 8, 4], dass:
- Wenn man einen [0] und zwei [0] Schritte vorwärts betrachtet, berücksichtigt das Programm alle möglichen Bewegungen, weil 0 ,
- [8] [8] , 8 “” , , ,
- Mit fünf oder mehr Schritten nach vorne [4] bewertet das Programm nicht mehr als vier „beste“ Züge.
Nachdem die Sortierung für den Alpha-Beta-Clipping-Algorithmus und einen ähnlichen Vektor in den Clipping-Einstellungen aktiviert war, verbrachte das Programm etwa 300 Millisekunden damit, eine quasi-optimale Bewegung auszuwählen und 8 Schritte vorwärts „tiefer zu gehen“.Heuristische Optimierung
Trotz der anständigen Anzahl von Scheitelpunktpositionen, die im Baum durchlaufen wurden und auf der Suche nach einer quasi optimalen Bewegung „tief“ nach vorne blickten, hatte die KI mehrere Schwächen. Ich habe eine davon als „ Kaninchenfalle “ definiert.Hasenfalle. ( 8 — 10 15), . “” ( !):
. :
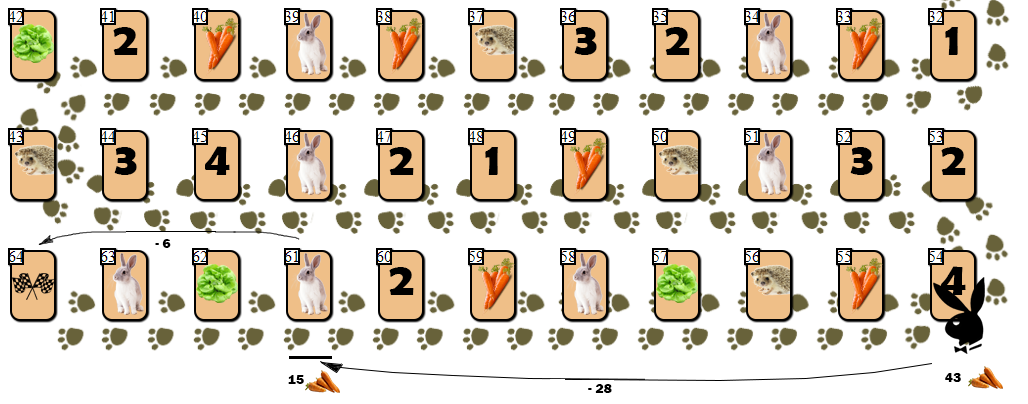
54 (43), — 10 55 . AI, , (61), 28 . , 6 9 ( 10 ).
, ( ), , 4 — 6 . , , , AI ?
,
, . AI . , , . “ ” :
65 — “” , , . , , , () .
Korrekturfaktoren
Unter Berufung auf die heuristische Formel zur Bewertung der aktuellen PositionE = Ks * S + Kc * C + Kp * P habeich bereits Korrekturfaktoren erwähnt, aber nicht beschrieben.Tatsache ist, dass sowohl die Formel selbst als auch die Funktionssätze wurden von mir intuitiv auf Basis des sogenannten abgeleitet "Gesunder Menschenverstand." Zumindest möchte ich solche Koeffizienten Ks, Kc und Kp auswählen, damit die Schätzung so angemessen wie möglich ist. Wie ist die „Angemessenheit“ der Bewertung zu bewerten? Die Bewertung ist eine dimensionslose Größe und kann nur mit einer anderen Schätzung verglichen werden. Ich konnte die einzige Möglichkeit finden, die Korrekturkoeffizienten zu verfeinern: Ichhabe eine Reihe von „Studien“ in das Programm aufgenommen, die in einer CSV-Datei mit Daten des Formulars gespeichert sind 45;26;2;f;29;19;0;f;2 ...
Diese Zeile bedeutet wörtlich Folgendes:- Der erste Spieler ist auf Feld 45, er hat 26 Karottenkarten und 2 Salatkarten in der Hand, der Spieler verpasst keinen Zug (f = falsch). Das Bewegungsrecht ist immer der erste Spieler.
- Der zweite Spieler in Zelle 29 mit 19 Karottenkarten und ohne Salatkarten verpasst keinen Zug.
- Die zweite Zahl bedeutet, dass ich bei der „Entscheidung“ für die Studie davon ausgegangen bin, dass sich der zweite Spieler in einer Gewinnsituation befindet.
Nachdem ich 20 Skizzen in das Programm aufgenommen hatte, lud ich sie in den Web-Client des Spiels herunter und sortierte dann jede skizzierte. Bei der Analyse der Skizze habe ich abwechselnd für jeden Spieler Züge gemacht, bis ich mich für den „Gewinner“ entschieden habe. Nachdem ich die Bewertung abgeschlossen hatte, schickte ich sie in einem speziellen Team an den Server.Nachdem ich 20 Etüden ausgewertet hatte (natürlich lohnt es sich, mehr davon zu analysieren), bewertete ich jede der Etüden durch das Programm. Bei der Auswertung werden die Werte der einzelnen Korrekturfaktoren von 0,5 bis 2 in Schritten von 0,1 - insgesamt angegeben = 4096 Varianten von Dreifachkoeffizienten. Wenn sich herausstellte, dass die Punktzahl für den ersten Spieler höher war als die Punktzahl des zweiten Spielers, und eine ähnliche Anweisung in der Zeile des Etüden-Datensatzes gespeichert wurde (der letzte Wert der Zeile ist 1), wurde der „Treffer“ gezählt. Ähnliches gilt für eine Spiegelsituation. Ansonsten wurde ein Beleg gezählt.Infolgedessen habe ich die Tripel ausgewählt, für die der Prozentsatz der „Treffer“ maximal war (16 von 20). Es kamen ungefähr 250 von 4096 Vektoren heraus, von denen ich die "besten" wieder "per Auge" auswählte und sie in den KI-Einstellungen installierte.Zusammenfassung
Als Ergebnis habe ich ein Arbeitsprogramm bekommen, das mich in der Regel in der Eins-zu-Eins-Version gegen den Computer schlägt. Ernste Statistiken über Siege und Niederlagen für die aktuelle Version des Programms wurden noch nicht gesammelt. Vielleicht macht die anschließende einfache KI-Abstimmung meine Siege unmöglich. Oder fast unmöglich, da der Hasenzellenfaktor immer noch besteht.Zum Beispiel würde ich in der Logik der Auswahl von Bewertungen (absolutes Maximum oder Maximum im Verhältnis zu anderen Spielern) definitiv eine Zwischenoption versuchen. Wenn der absolute Wert der Punktzahl des i-ten Spielers gleich ist, ist es zumindest sinnvoll, einen Zug zu wählen, der zu einer Position mit einem höheren relativen Wert der Punktzahl führt (eine Mischung aus dem edlen Leslie und dem tückischen Feith).Das Programm ist für die Version mit 3 Spielern voll funktionsfähig. Es besteht jedoch der Verdacht, dass die „Qualität“ der KI-Bewegungen beim Spielen mit 3 Spielern geringer ist als beim Spielen mit zwei Spielern. Während des letzten Tests verlor ich jedoch gegen den Computer - vielleicht fahrlässig, indem ich beiläufig die Menge der Karotten in meinen Händen auswertete und mit einem Überschuss an „Kraftstoff“ ins Ziel kam.Bisher wird die Weiterentwicklung der KI durch das Fehlen einer Person behindert - eines „Testers“, dh eines lebenden Gegners eines Computer- „Genies“. Ich selbst habe genug von Hare und Hedgehog gespielt, um Übelkeit zu bekommen, und war gezwungen, in der gegenwärtigen Phase zu unterbrechen.→ Link zum Repository mit Quelle