Mathe in Gamedev ist einfach. Matrizen und affine Transformationen

Hallo allerseits! Mein Name ist Grisha und ich bin der Gründer von CGDevs. Heute möchte ich das Thema Mathematik in der Spieleentwicklung fortsetzen. In einem früheren Artikel haben wir grundlegende Beispiele für die Verwendung von Vektoren und Integralen in Unity-Projekten gezeigt. Lassen Sie uns nun über Matrizen und affine Transformationen sprechen. Wenn Sie sich mit Matrixarithmetik auskennen; Sie wissen, was TRS ist und wie Sie damit arbeiten können. Was ist die Householder-Transformation? Sie werden wahrscheinlich nichts Neues für sich finden. Wir werden im Zusammenhang mit 3D-Grafiken sprechen. Wenn Sie sich für dieses Thema interessieren - willkommen bei cat.



Beginnen wir mit einem der wichtigsten Konzepte im Kontext des Artikels - affine Transformationen . Affine Transformationen sind im Wesentlichen die Transformation des Koordinatensystems (oder des Raums) durch Multiplikation des Vektors mit einer speziellen Matrix. Zum Beispiel Transformationen wie Bewegung, Rotation, Skalierung, Reflexion usw. Die Haupteigenschaften affiner Transformationen sind, dass Sie im selben Raum bleiben (es ist unmöglich, einen zweidimensionalen Vektor aus zweidimensional zu erstellen) und dass die Linien sich schneiden / parallel sind Wurde vor der Konvertierung gekreuzt, bleibt diese Eigenschaft nach der Konvertierung erhalten. Darüber hinaus verfügen sie über viele mathematische Eigenschaften, die Kenntnisse der Theorie von Gruppen, Mengen und linearer Algebra erfordern, was die Arbeit mit ihnen erleichtert.

TRS-Matrix

Das zweite wichtige Konzept in der Computergrafik ist die TRS-Matrix . Mithilfe dieser Funktion können Sie die häufigsten Vorgänge beschreiben, die beim Arbeiten mit Computergrafiken verwendet werden. Eine TRS-Matrix besteht aus drei Transformationsmatrizen. Verschiebungsmatrizen (Translation), Rotation um jede Achse (Rotation) und Skalierung (Scale).
Sie sieht so aus.



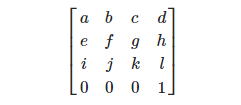
Wo:
Die Bewegung ist t = neuer Vektor3 (d, h, l).
Skalierung - s = neuer Vektor3 (neuer Vektor3 (a, e, i) .Magnitude, neuer Vector3 (b, f, j) .Magnitude, neuer Vector3 (c, g, k) .Magnitude);

Eine Rotation ist eine Matrix der Form:



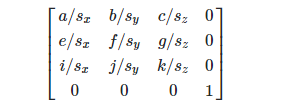
Lassen Sie uns nun etwas tiefer in den Kontext der Einheit gehen. Zunächst ist die TRS-Matrix eine sehr praktische Sache, sollte aber nicht überall verwendet werden. Da eine einfache Anzeige der Position oder Addition von Vektoren in einer Einheit schneller funktioniert, sind Matrizen in vielen mathematischen Algorithmen um ein Vielfaches bequemer als Vektoren. Die TRS-Funktionalität in Unity ist weitgehend in der Matrix4x4- Klasse implementiert, aus Sicht der Anwendung jedoch nicht praktisch. Da die Matrix nicht nur durch Multiplikation angewendet werden kann, sondern im Allgemeinen auch Informationen zur Ausrichtung des Objekts speichern kann, möchte ich für einige Transformationen nicht nur die Position berechnen, sondern auch die Ausrichtung des gesamten Objekts ändern können (z. B. Reflexion, die nicht in Unity implementiert ist).

Alle Beispiele für das lokale Koordinatensystem sind nachstehend aufgeführt (der Ursprung des GameObject wird als Ursprung der Koordinaten betrachtet, innerhalb derer sich das Objekt befindet. Wenn das Objekt die Wurzel der Hierarchie in der Einheit ist, ist der Ursprung die Welt (0,0,0)).

Da wir mit der TRS-Matrix grundsätzlich die Position eines Objekts im Raum beschreiben können, benötigen wir eine Zerlegung von TRS zu den spezifischen Werten für Position, Rotation und Skalierung für Unity. Dazu können Sie Erweiterungsmethoden für die Matrix4x4-Klasse schreiben


Darüber hinaus können Sie für eine bequeme Arbeit einige Erweiterungen der Transform-Klasse implementieren, um mit TRS darin zu arbeiten.


Damit enden die Vorteile der Einheit, da die Matrizen in der Einheit im Betrieb sehr schlecht sind. Viele Algorithmen erfordern eine Matrixarithmetik, die selbst in vollständig einfachen Operationen wie dem Hinzufügen von Matrizen und dem Multiplizieren von Matrizen mit einem Skalar nicht in der Einheit implementiert ist. Aufgrund der Besonderheit der Implementierung von Vektoren in Unity3d gibt es außerdem eine Reihe von Unannehmlichkeiten, die mit der Tatsache verbunden sind, dass Sie einen 4x4-Vektor erstellen können, aber nicht sofort 1x4 erstellen können. Da wir mehr über die Transformation des Haushaltsinhabers für Überlegungen sprechen werden, implementieren wir zunächst die dafür erforderlichen Operationen.

Das Addieren / Subtrahieren und Multiplizieren mit einem Skalar ist einfach. Es sieht ziemlich sperrig aus, aber hier gibt es nichts Kompliziertes, da die Arithmetik einfach ist.


Zur Reflexion benötigen wir jedoch die Operation der Matrixmultiplikation in einem bestimmten Fall. Multiplikation eines Vektors der Dimension 4x4 mit 1x4 (transponiert) Wenn Sie mit der Matrixmathematik vertraut sind, wissen Sie, dass Sie bei dieser Multiplikation die extremen Zahlen der Dimension betrachten müssen, und Sie erhalten die Dimension der Matrix am Ausgang, dh in diesem Fall 4x4. Es gibt genügend Informationen darüber, wie Matrizen multipliziert werden, daher werden wir dies nicht malen. Hier ist ein Beispiel für einen bestimmten Fall, der sich in Zukunft als nützlich erweisen wird.

Transformation der Haushalte

Auf der Suche nach der Reflektion eines Objekts relativ zu einer Achse stoße ich häufig auf Ratschläge, eine negative Skala in die erforderliche Richtung zu setzen. Dies ist im Kontext von Unity ein sehr schlechter Rat, da viele Systeme in der Engine beschädigt werden (Butching, Kollisionen usw.). In einigen Algorithmen wird dies zu nicht trivialen Berechnungen, wenn Sie in Bezug auf Vector3.up oder Vector3.forward nicht trivial reflektieren müssen. aber in eine beliebige Richtung. Die Reflexionsmethode in einer Einheit außerhalb der Box selbst ist nicht implementiert, daher habe ich die Householder-Methode implementiert.

Die Householder-Transformation wird nicht nur in der Computergrafik verwendet, sondern ist in diesem Zusammenhang eine lineare Transformation, die ein Objekt relativ zu einer Ebene widerspiegelt, die durch den „Ursprung“ verläuft und durch die Normale zur Ebene bestimmt wird. In vielen Quellen wird es ziemlich kompliziert und unverständlich beschrieben, obwohl seine Formel elementar ist.

H = I-2 * n * (n ^ T)

Wenn H die Transformationsmatrix ist, ist I in unserem Fall Matrix4x4.identity und n = neuer Vektor4 (planeNormal.x, planeNormal.y, planeNormal.z, 0). Das Symbol T bedeutet Transposition, dh nach Multiplikation von n * (n ^ T) erhalten wir eine 4x4-Matrix.

Die implementierten Methoden werden sich als nützlich erweisen und die Aufnahme wird sehr kompakt sein.


Wichtig: planeNormal sollte normalisiert werden (was logisch ist) und die letzte Koordinate n sollte 0 sein, damit sich die Dehnung in Richtung nicht auswirkt, da dies von der Länge des Vektors n abhängt.

Zur Vereinfachung in Unity implementieren wir jetzt die Erweiterungsmethode für die Transformation


Das ist alles für heute, wenn diese Artikelserie weiterhin interessant sein wird, werde ich auch andere Anwendungen der Mathematik in der Spieleentwicklung aufzeigen. Dieses Mal wird es kein Projekt geben, da der gesamte Code im Artikel platziert ist, aber das Projekt mit der spezifischen Anwendung wird im nächsten Artikel enthalten sein. Auf dem Bild können Sie erraten, worum es im nächsten Artikel geht.



Vielen Dank für Ihre Aufmerksamkeit!