Benötigen Sie mehr verschiedene Unschärfen

Bildunschärfe mit dem Gaußschen Unschärfefilter wird häufig für eine Vielzahl von Aufgaben verwendet. Aber manchmal möchten Sie für alle Gelegenheiten etwas mehr Abwechslung als nur einen Filter, bei dem sich nur ein Parameter zur Anpassung eignet - seine Größe. In diesem Artikel werden wir uns einige andere Unschärfeimplementierungen ansehen.

Einführung

Der Gaußsche Unschärfeeffekt ist eine lineare Operation und repräsentiert mathematisch eine Faltung des Bildes mit der Filtermatrix. In diesem Fall wird jedes Pixel im Bild durch die Summe der in der Nähe befindlichen Pixel ersetzt, die mit bestimmten Gewichtungsfaktoren aufgenommen wurden.

Der Filter heißt Gauß, weil er aus einer Funktion aufgebaut ist, die als Gauß bekannt ist. $$$e ^ {- x ^ 2}$ ::



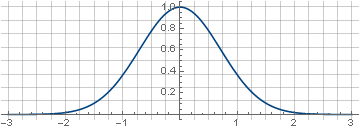
eine zweidimensionale Version davon wird durch ihre Drehung um die Ordinatenachse erhalten, $$$e ^ {- (x ^ 2 + y ^ 2)}$ ::



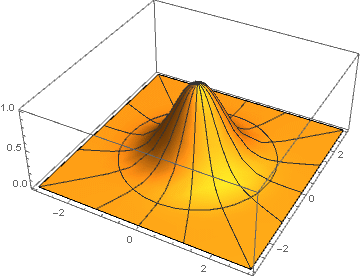
Hier für jedes Koordinatenpaar $$$(x, y)$ Der Abstand zum Zentrum wird nach der Formel berechnet $$$\ sqrt {x ^ 2 + y ^ 2}$ , die als Argument an die Gaußsche Funktion übergeben wird - und, wie Sie leicht sehen können, $$$e ^ {- \ left (\ sqrt {x ^ 2 + y ^ 2} \ right) ^ 2}$ reduziert auf $$$e ^ {- (x ^ 2 + y ^ 2)}$ .

Matrix auf einem Segment aufgebaut $$$[- 3.3]$ und mit einem gewissen Grad an Stichproben wird es so aussehen:

$$

$$\ left (\ begin {array} {ccccccc} 1,52 \ mal 10 ^ {- 8} & 2,26 \ mal 10 ^ {- 6} & 0,0000454 & 0,000123 & 0,0000454 & 2,26 \ mal 10 ^ {- 6} & 1,52 \ mal 10 ^ {- 8} \\ 2,26 \ mal 10 ^ {- 6} & 0,000335 & 0,00674 & 0,0183 & 0,00674 & 0,000335 & 2,26 \ mal 10 ^ {- 6} \\ 0,0000454 & 0,00674 & 0,135 & 0,368 & 0,135 & 0,00674 & 0,0000454 \\ 0,000123 & 0,0183 & 0,368 & 1,00 & 0,368 & 0,0183 & 0,000123 \\ 0,0000454 & 0,00674 & 0,135 & 0,368 & 0,135 & 0,00674 & 0,0000454 \\ 2,26 \ mal 10 ^ {- 6} & 0,000335 & 0,00674 & 0,0183 & 0,00674 & 0,000335 & 2,26 \ mal 10 ^ {- 6} \\ 1,52 \ mal 10 ^ {- 8} & 2,26 \ mal 10 ^ {- 6} & 0,0000454 & 0,000123 & 0,0000454 & 2,26 \ mal 10 ^ { -6} & 1,52 \ mal 10 ^ {- 8} \\ \ end {array} \ right)$$

Oder wenn wir die Werte der Matrixelemente als Helligkeitsstufe betrachten, wie folgt:



In Bezug auf die Signalverarbeitung wird dies als Impulsantwort bezeichnet, da genau dies das Ergebnis der Faltung dieses Filters mit einem einzelnen Impuls (in diesem Fall einem Pixel) ist.

Zunächst wird ein Gaußscher Wert in einem unendlichen Intervall definiert. Aufgrund der Tatsache, dass es ziemlich schnell abfällt, ist es jedoch möglich, Werte nahe Null von den Berechnungen auszuschließen, da sie das Ergebnis immer noch nicht beeinflussen. In realen Anwendungen ist auch eine Wertnormalisierung erforderlich, damit sich die Bildhelligkeit nach der Faltung nicht ändert. und im Fall der Unschärfe eines Bildes, in dem jedes Pixel die gleiche Farbe hat, sollte sich das Bild selbst nicht ändern.

Der Einfachheit halber wird die Normalisierung häufig auch in Koordinaten verwendet, indem ein zusätzlicher Parameter eingeführt wird $$$\ sigma$ (gelesen als "Sigma") - um ein Argument im Bereich zu betrachten $$$[- 1,1]$ und $$$\ sigma$ bestimmt das Kompressionsverhältnis des Gaußschen:

$$

$$\ frac {e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}}} {2 \ pi \ sigma ^ 2}$$

Teiler normalisieren $$$2 \ pi \ sigma ^ 2$ hier analytisch durch ein bestimmtes Integral im Unendlichen erhalten:

$$

$$\ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}} \, dx dy = 2 \ pi \ sigma ^ 2$$

Aufgrund der Tatsache, dass Gleichheit gilt $$$e ^ {- \ left (x ^ 2 + y ^ 2 \ right)} = e ^ {- x ^ 2} e ^ {- y ^ 2}$ Gaußsche Unschärfe kann nacheinander implementiert werden, zuerst in Zeilen und dann in Spalten - wodurch Sie eine Menge an Berechnungen sparen können. In diesem Fall muss die Normalisierungsformel für den eindimensionalen Fall verwendet werden -

$$

$$\ frac {e ^ {- \ frac {x ^ 2} {2 \ sigma ^ 2}}} {\ sqrt {2 \ pi \ sigma ^ 2}}$$

Starten Sie

Für einen beliebigen Filter müssen wir zunächst unsere eigene Dämpfungsfunktion aus einer Variablen definieren $$$f$ , aus dem die Funktion zweier Variablen durch Rotation durch Ersetzen erhalten wird $$$x$ auf $$$\ sqrt {x ^ 2 + y ^ 2}$ wo $$$x$ und $$$y$ Dies sind die Koordinaten des Matrixelements im Bereich $$$(- 1,1)$ und wird dann verwendet, um die Elemente der Matrix zu füllen. Die Normalisierung wird nicht analytisch betrachtet, sondern eine direkte Summierung aller Elemente der Matrix - dies ist sowohl einfacher als auch genauer -, da die Funktion nach der Diskretisierung „ausgedünnt“ wird und der Normalisierungswert vom Diskretisierungsgrad abhängt.

Falls die Matrixelemente von Grund auf neu nummeriert sind, die Koordinate $$$x$ oder $$$y$ wird nach der Formel berechnet

$$

$$\ frac {2 index} {size-1} -1$$

wo $$$index$ - die Seriennummer des Elements in der Zeile oder Spalte und $$$size$ - Gesamtzahl der Elemente.

Für eine 5 x 5-Matrix würde dies beispielsweise folgendermaßen aussehen:

$$

$$\ left (\ begin {array} {ccccc} f (-1, -1) & f \ left (- \ frac {1} {2}, - 1 \ right) & f (0, -1) & f \ left (\ frac {1} {2}, - 1 \ right) & f (1, -1) \\ f \ left (-1, - \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2}, - \ frac {1} {2} \ rechts) & f \ links (0, - \ frac {1} {2} \ rechts) & f \ links (\ frac { 1} {2}, - \ frac {1} {2} \ rechts) & f \ links (1, - \ frac {1} {2} \ rechts) \\ f (-1,0) & f \ links (- \ frac {1} {2}, 0 \ rechts) & f (0,0) & f \ links (\ frac {1} {2}, 0 \ rechts) & f (1,0) \\ f \ left (-1, \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2}, \ frac {1} {2} \ right) & f \ left (0, \ frac {1} {2} \ rechts) & f \ links (\ frac {1} {2}, \ frac {1} {2} \ rechts) & f \ links (1, \ frac {1} {2 } \ rechts) \\ f (-1,1) & f \ links (- \ frac {1} {2}, 1 \ rechts) & f (0,1) & f \ links (\ frac {1} { 2}, 1 \ right) & f (1,1) \\ \ end {array} \ right)$$

Wenn wir Grenzwerte ausschließen, die noch Null sind, werden die Koordinaten nach der Formel berechnet

$$

$$\ frac {2 Indexgröße + 1} {Größe}$$

und die Matrix wird dementsprechend die Form annehmen

$$

$$\ left (\ begin {array} {ccccc} f \ left (- \ frac {4} {5}, - \ frac {4} {5} \ right) & f \ left (- \ frac {2} { 5}, - \ frac {4} {5} \ rechts) & f \ links (0, - \ frac {4} {5} \ rechts) & f \ links (\ frac {2} {5}, - \ frac {4} {5} \ rechts) & f \ links (\ frac {4} {5}, - \ frac {4} {5} \ rechts) \\ f \ links (- \ frac {4} {5 }, - \ frac {2} {5} \ right) & f \ left (- \ frac {2} {5}, - \ frac {2} {5} \ right) & f \ left (0, - \ frac {2} {5} \ rechts) & f \ links (\ frac {2} {5}, - \ frac {2} {5} \ rechts) & f \ links (\ frac {4} {5}, - \ frac {2} {5} \ rechts) \\ f \ links (- \ frac {4} {5}, 0 \ rechts) & f \ links (- \ frac {2} {5}, 0 \ rechts ) & f (0,0) & f \ links (\ frac {2} {5}, 0 \ rechts) & f \ links (\ frac {4} {5}, 0 \ rechts) \\ f \ links ( - \ frac {4} {5}, \ frac {2} {5} \ rechts) & f \ links (- \ frac {2} {5}, \ frac {2} {5} \ rechts) & f \ links (0, \ frac {2} {5} \ rechts) & f \ links (\ frac {2} {5}, \ frac {2} {5} \ rechts) & f \ links (\ frac {4} {5}, \ frac {2} {5} \ rechts) \\ f \ links (- \ frac {4} {5}, \ frac {4} {5} \ rechts) & f \ links (- \ frac {2} {5}, \ frac {4} {5} \ rechts) & f \ links (0, \ frac {4} {5} \ rechts) & f \ links (\ frac {2} {5}, \ frac {4} {5} \ right) & f \ left (\ frac {4} {5}, \ frac {4} {5} \ right) \\ \ end {array} \ right)$$

Nachdem die Matrixelemente durch die Formel berechnet wurden, ist es notwendig, ihre Summe zu berechnen und die Matrix darin zu teilen. Zum Beispiel, wenn wir eine Matrix bekommen

$$

$$\ left (\ begin {array} {ccc} 1 & 4 & 1 \\ 4 & 20 & 4 \\ 1 & 4 & 1 \\ \ end {array} \ right)$$

dann ist die Summe aller seiner Elemente 40 und nach der Normalisierung nimmt sie die Form an

$$

$$\ left (\ begin {array} {ccc} \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ frac {1} {10} & \ frac {1} {2} & \ frac {1} {10} \\ \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ end {array } \ right)$$

und die Summe aller seiner Elemente wird 1.

Lineare Dämpfung

Nehmen Sie zunächst die einfachste Funktion - die Zeile:

$$

$$\ left \ {\ begin {array} {ll} 1-x, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

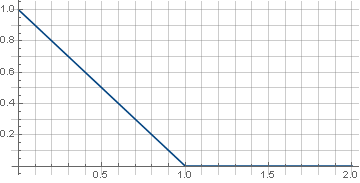
Eine stückweise kontinuierliche Definition erfordert hier, dass die Funktion garantiert auf Null geht und während der Drehung keine Artefakte an den Ecken der Matrix auftreten. Da die Drehung die Wurzel der Summe der Quadrate der Koordinaten verwendet, die immer positiv ist, reicht es außerdem aus, die Funktion nur im positiven Teil der Werte zu bestimmen. Als Ergebnis erhalten wir:

Weiche lineare Dämpfung

Ein scharfer Übergang von einer schrägen Linie zu Nullfunktionen kann einen Widerspruch mit einem Sinn für Schönheit verursachen. Um es zu lösen, hilft uns die Funktion.

$$

$$1- \ frac {n x-x ^ n} {n-1}$$

in dem $$$n$ bestimmt die "Steifigkeit" des Andockens, $$$n> 1$ . Zum Beispiel $$$n = 3$ wir bekommen

$$

$$\ left \ {\ begin {array} {ll} 1- \ frac {3 xx ^ 3} {2}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

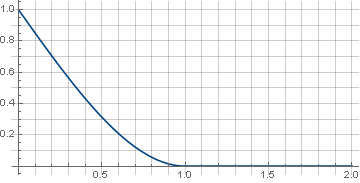
und der Filter selbst wird so aussehen

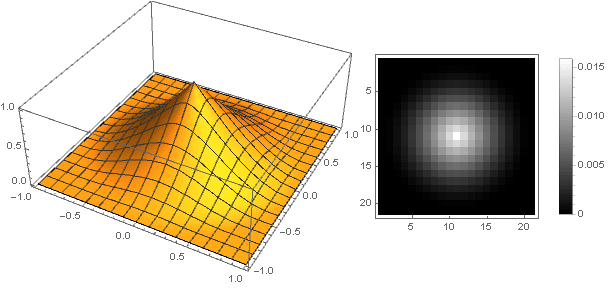
Hyperbolische Dämpfung

Der Filter kann „schärfer“ und sanfter auf Null gestellt werden, indem eine andere Funktion, beispielsweise eine Hyperbel, übernommen wird, und durch Summieren mit einer Parabel ein reibungsloser Übergang auf Null sichergestellt werden.



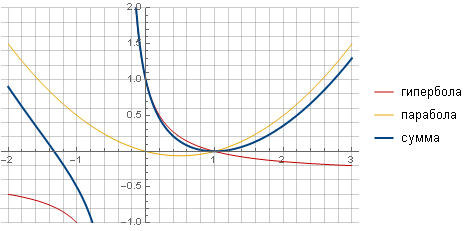
Nach all den Berechnungen und Vereinfachungen erhalten wir die Formel

$$

$$\ left \ {\ begin {array} {ll} \ frac {(x-1) ^ 2 (k x + k + 1)} {(k + 1) (k x + 1)}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

in welchem ​​Parameter $$$k> 0$ bestimmt die Art der Dämpfung:



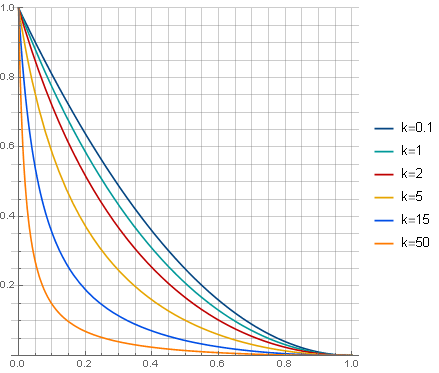
und der Filter selbst wird suchen (nach $$$k = 5$ ) wie

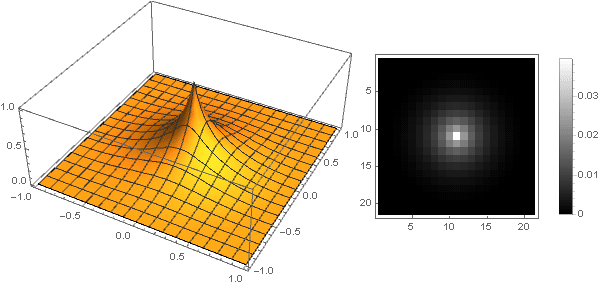
Bokeh-Effekt

Sie können einen anderen Weg gehen - um die Oberseite des Filters nicht scharf, sondern dumm zu machen. Der einfachste Weg, dies zu implementieren, besteht darin, die Dämpfungsfunktion als Konstante festzulegen:

$$

$$\ left \ {\ begin {array} {ll} 1, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

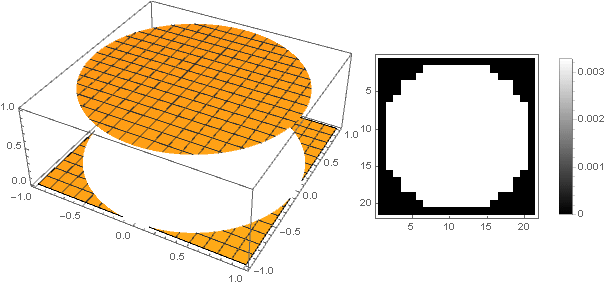
In diesem Fall erhalten wir jedoch eine starke Pixelung, die im Gegensatz zum Sinn für Schönheit steht. Um es an den Rändern glatter zu machen, hilft uns eine Parabel höherer Ordnung, von der wir durch Bewegen entlang der Ordinatenachse und Quadrieren erhalten

$$

$$\ left \ {\ begin {array} {ll} \ left (1-x ^ n \ right) ^ 2, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

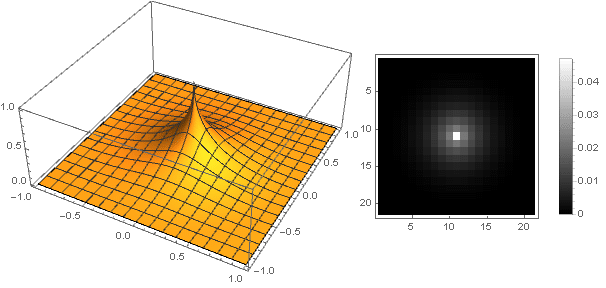
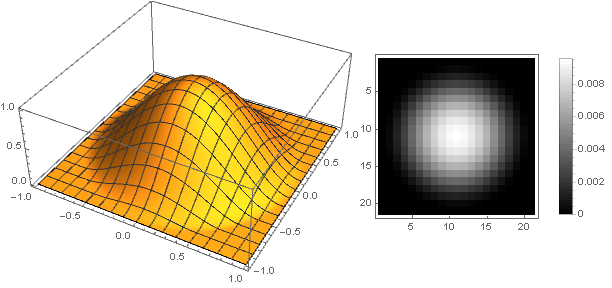
Variierender Parameter $$$n$ Sie können eine Vielzahl von Filteroptionen erhalten:

$$

$$n = 0,5$$

$$

$$n = 2$$

$$

$$n = 10$$

$$

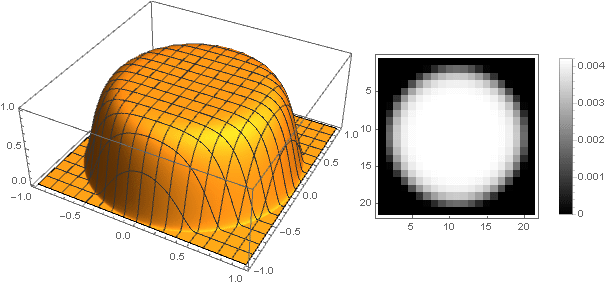
$$n = 50$$

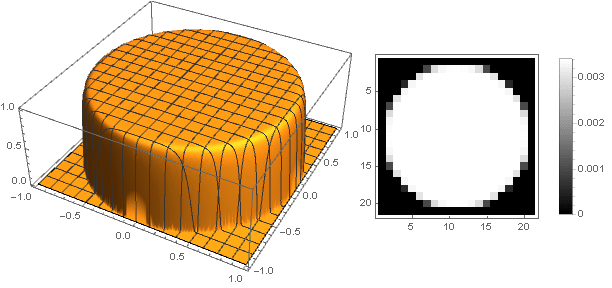
Und indem Sie die Dämpfungsfunktion leicht ändern, können Sie den Ring an den Rändern des Filters stärker ausdrücken, zum Beispiel wie folgt:

$$

$$\ left \ {\ begin {array} {ll} \ left (1-x ^ n \ right) ^ 2 \ left (d + x ^ m \ right), & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

Hier Parameter $$$d$ bestimmt die Höhe des Zentrums und $$$m$ - die Schärfe des Übergangs zu den Kanten.
Für $$$d = 0,2, m = 2, n = 10$ wir bekommen



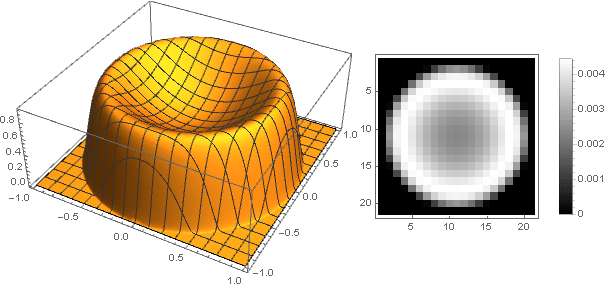
aber für $$$d = 0, m = 12, n = 2$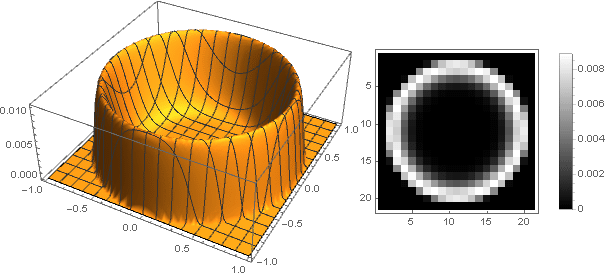

Gaußsche Variationen

Die Funktion des Gaußschen selbst kann auch direkt geändert werden. Der naheliegendste Weg, dies zu tun, besteht darin, den Exponenten zu parametrisieren - wir werden ihn jetzt nicht betrachten, sondern eine interessantere Option wählen:

$$

$$\ left \ {\ begin {array} {ll} e ^ {\ frac {kx ^ 2} {x ^ 2-1}}, & -1 <x <1 \\ 0, andernfalls \\ \ end { Array} \ right.$$

Aufgrund der Tatsache, dass mit $$$x$ Einheitsnenner $$$x ^ 2-1$ neigt zu Null Bruch $$$\ frac {k x ^ 2} {x ^ 2-1}$ neigt dazu, unendlich zu minus, und der Exponent selbst tendiert auch zu null. Also dividieren durch $$$x ^ 2-1$ ermöglicht das Komprimieren des Bereichs der Funktionsdefinition mit $$$(- \ infty, \ infty)$ vorher $$$(- 1,1)$ . Darüber hinaus, wenn $$$x = \ pm 1$ aufgrund der Division durch Null ( $$$1 ^ 2-1 = 0$ ) Der Wert der Funktion ist nicht definiert, hat aber zwei Grenzen - die Grenze einerseits (von innen) ist Null und andererseits unendlich:

$$

$$\ underset {x \ bis 1 ^ -} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = 0$$

$$

$$\ underset {x \ bis 1 ^ +} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = \ infty$$

Da die Grenzwerte nicht im Intervall enthalten sind, reicht eine Null im Grenzwert nur auf einer Seite völlig aus. Interessanterweise erstreckt sich diese Eigenschaft auf alle Ableitungen dieser Funktion, was eine perfekte Übereinstimmung mit Null gewährleistet.

Parameter $$$k$ bestimmt die Ähnlichkeit mit dem Gaußschen - je größer er ist, desto stärker wird die Ähnlichkeit erhalten - aufgrund der Tatsache, dass ein zunehmend linearer Abschnitt $$$\ frac {1} {x ^ 2-1}$ fallen in die Mitte der Funktion. Man könnte davon ausgehen, dass man aus diesem Grund im Limit den ursprünglichen Gaußschen erhalten kann - aber leider nein - die Funktionen sind immer noch unterschiedlich.



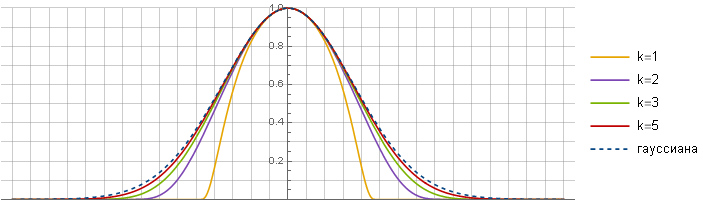
Jetzt können Sie sehen, was passiert ist:

$$

$$k = 5$$

$$

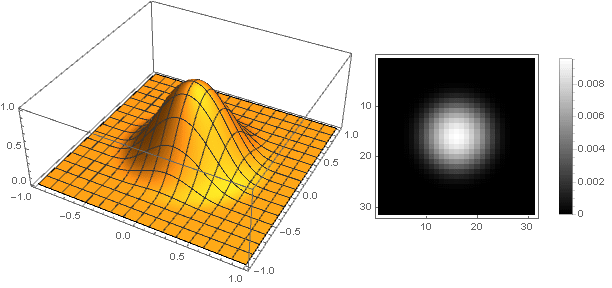
$$k = 2$$

$$

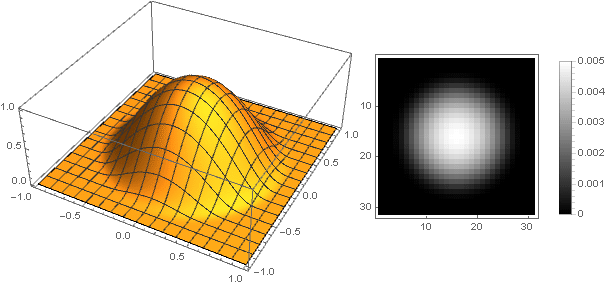
$$k = 0,5$$

$$

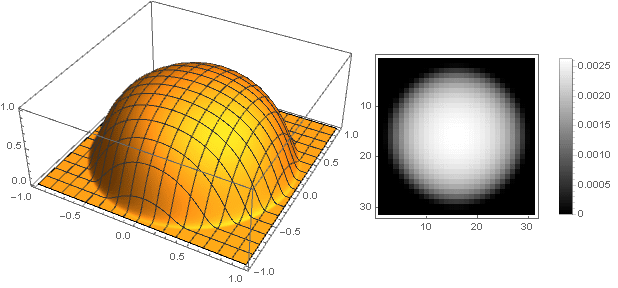
$$k = 0,1$$

$$

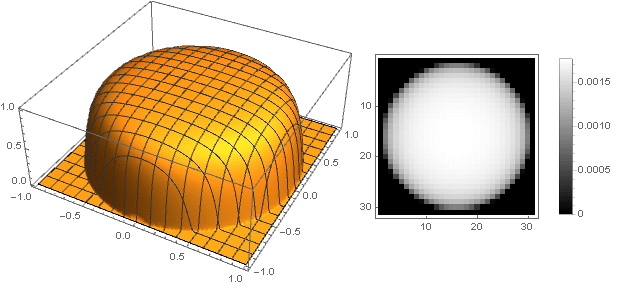
$$k = 0,01$$

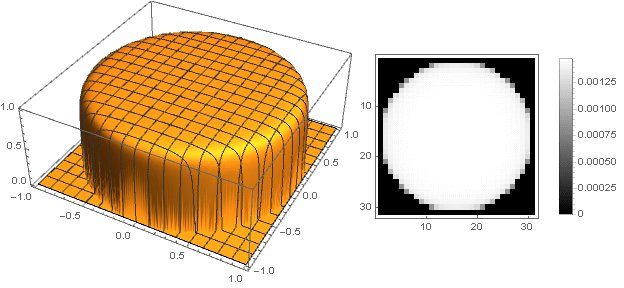
Formvariationen

Durch Ändern der Übergangsfunktion von zwei Koordinaten auf eine $$$\ sqrt {x ^ 2 + y ^ 2}$ können Sie andere Formen erhalten, nicht nur eine Scheibe. Zum Beispiel:

$$

$$f \ left (\ frac {\ left | x-y \ right | + \ left | x + y \ right |} {2} \ right)$$

$$

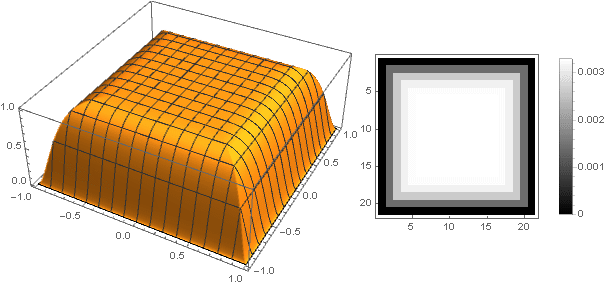
$$f (\ left | x \ right | + \ left | y \ right |)$$

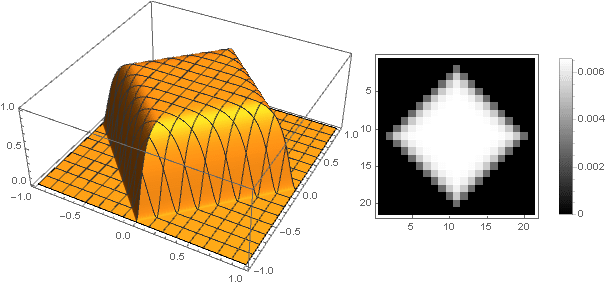
Wenn Sie zu komplexen Zahlen wechseln, können Sie komplexere Zahlen konstruieren:

$$

$$f \ left (\ frac {\ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {0} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {3}} \ rechts) \ rechts | + \ links | \ Re \ links ((x + iy) (-1) ^ {\ frac { 2} {3}} \ right) \ right |} {\ sqrt {3}} \ right)$$

$$

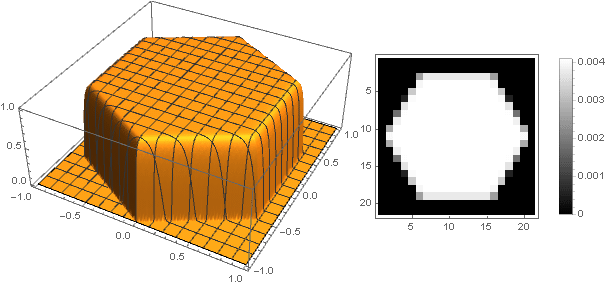
$$f \ biggl (10 \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {8}} \ right) \ right | \ biggr) \ cdot f (\ left | x + iy \ right |)$$

$$

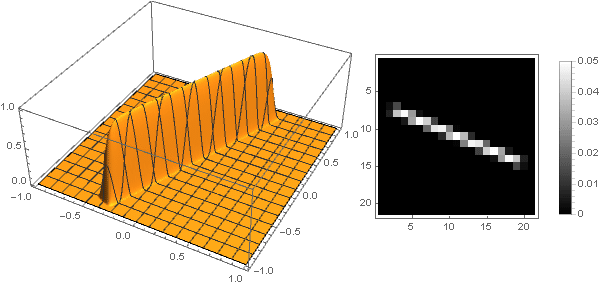
$$f \ biggl (\ biggl | 5 \ left | x + iy \ right | (x + iy) \ Re \ biggl (\ cos \ left (\ frac {5} {2} \ arg (x + iy) \ right ) \ biggr) \ biggr | \ biggr) \ cdot f (\ left | x + iy \ right |)$$

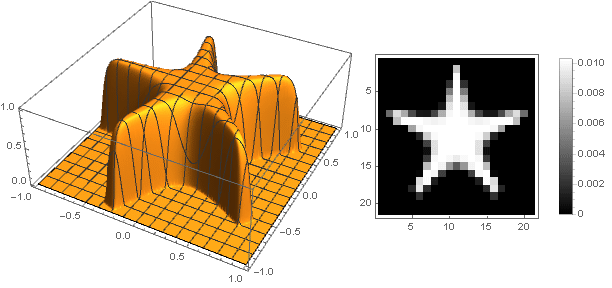
In diesem Fall müssen Sie sicherstellen, dass beim Konvertieren von Koordinaten das Intervall nicht überschritten wird $$$(0,1)$ - Nun, oder umgekehrt, definieren Sie die Dämpfungsfunktion für negative Werte des Arguments neu.

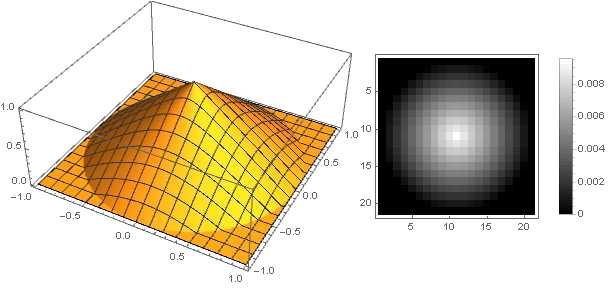
Einige konkrete Beispiele

Ein Artikel wäre ohne praktische Tests an bestimmten Bildern nicht vollständig. Da wir keine wissenschaftliche Arbeit haben, werden wir auch nicht das Bild von Lena aufnehmen - wir werden etwas Weiches und Flauschiges nehmen:


















Die gleichen Filter, aber für Text:

Fazit

In ähnlicher Weise können Sie komplexere Filter erstellen, einschließlich solcher mit Schärfen oder Konturen. und ändern Sie auch die bereits berücksichtigten.

Von besonderem Interesse ist die nichtlineare Filterung, wenn die Werte der Filterkoeffizienten von den Koordinaten oder dem direkt gefilterten Bild abhängen - dies ist jedoch bereits Gegenstand anderer Studien.

Im Einzelnen wird hier die Ableitung von Funktionen zum Andocken an eine Konstante betrachtet. Die hier betrachteten Fensterfunktionen können auch als Dämpfungsfunktion verwendet werden. Sie müssen lediglich das Argument c (0,1) auf (skalieren) $$$\ frac {1} {2}$ , 1) oder zunächst Fensterfunktionen nach der Formel betrachten $$$\ frac {1} {2} \ left (f \ left (\ frac {t x + 1} {t-1} \ right) -f \ left (\ frac {t x-1} {t-1} \ right) \ right)$ .

Das Wolfram Mathematica-Quelldokument für diesen Artikel kann hier heruntergeladen werden .