Anstelle des Vorworts
Angenommen, als Sie abends im warmen Sessel saßen, kam Ihnen ein verrückter Gedanke: "Hmm, warum finde ich nicht heraus, warum die Hyperparameter des Modells zufällig ausgewählt werden und warum alles funktioniert?"
Dies ist ein rutschiger Hang - Sie denken, ein paar Abende mit einer gemütlichen Lektüre des Kapitels „Deep Learning“ oder 5-minütigen Youtube-Clips aus verschiedenen MOOCs reichen aus; Um Verständnis und nicht seine Illusion zu schaffen, ist eine angemessene Zeit erforderlich (für die Fanatiker sicherlich nicht weniger als sechs Monate). Das Traurigste ist jedoch, dass der Gewinn aus diesem Ereignis nicht offensichtlich ist - zum Glück (oder leider) ist die Welt nicht nach den Gesetzen der Mathematik geordnet, und wenn Sie dreimal Doktor der Physik und Physik sind, funktionieren einige Modelle nur dann besser, wenn Sie einwerfen Sie haben mehr vorverarbeitete Daten oder bilden ein riesiges Ensemble.
Ich betrachte es als meine Pflicht, Sie zu warnen, dass dies ein Kurvenpfad ist, und es ist möglich, dass sich Investitionen in Mathematik nicht auszahlen, sobald wir möchten. Aber Mathematik ist an sich interessant, unabhängig von den Anwendungen. Wenn Sie interessiert sind und wissen, was in dieser Black Box mit Hyperparametern passiert, bedeutet dies außerdem, dass Ihnen die Mathematik höchstwahrscheinlich nicht gleichgültig ist.
Noch etwas zu meinen Empfehlungen: Ich mag keine mathematische Literatur, die voller Indizes, Perlen wie „a_ijk mit drei Unterstrichen und einem konjugierten Hut“ ist. Ich glaube, dass Ideen wichtiger sind als strenge Schlussfolgerungen. Gleichzeitig sollten Ideen nicht in „Hände“ geraten, alles sollte recht streng sein. Ich mag keine Bücher wie Bourbaki und Knut. Meiner Meinung nach sind diese Bücher für alles gedacht, aber nicht zum Lesen und nicht zum Studieren des Themas. Sie sind gut als Links und als Enzyklopädien.
Am Ende werde ich etwas von Bertrand Russell zitieren:
Euklid verachtete den praktischen Nutzen, den Platon einführte. Sie sagen, dass ein Student, nachdem er die Beweise angehört hatte, fragte, was er durch das Studium der Geometrie gewonnen habe; dann rief Euklid einen Sklaven an und sagte: "Gib dem jungen Mann einen Cent, denn er muss sicherlich von dem profitieren, was er studiert."
Jetzt gehe ich zum Hauptteil über.
Voraussetzungen
- Ich gehe davon aus, dass Sie sich mehr oder weniger an einem Mathematikkurs orientieren.
- Ich gehe davon aus, dass Sie mit „Ihnen“ nicht ganz auf Englisch sind, da viele gute Literatur und Kurse in dieser Sprache geschrieben und erzählt werden. Mathematisches Englisch ist nicht so beängstigend wie Englisch im Allgemeinen; Dies ist ein eher begrenztes Vokabular mit normal aufgebauten Sätzen, ohne Zeitmischung, ohne Farbenrausch usw.
- Ich gehe davon aus, dass Sie ein Seil haben, mit dem Sie sich an einen Stuhl binden können.
Schwierigkeitsgrad
Es ist kein Geheimnis, dass zu jeder mathematischen Disziplin viel Literatur geschrieben wurde, und manchmal wird sogar die einfache Auswahl des richtigen Buches zum Problem. Ich werde einige Komplexitätsebenen in der Literatur hervorheben, von denen Sie wussten, wo Sie sich einmischen und wo Sie klettern mussten (bisher), was nicht erforderlich war (oder woran Sie sich wenden können, um umfassendere Informationen zu erhalten).
- Bring es an - das Hauptarbeitspferd; Dies sind Bücher, die als "Muss" bezeichnet werden.
- Tut mir sehr weh - eine Stufe höher, ermöglicht es Ihnen, Stufe 1 aus der Vogelperspektive zu betrachten, Wissen zu systematisieren, verschiedene Wissensbereiche zu kombinieren.
- Albtraum - für die Starken im Geist, das Niveau von Mehmat, für Liebhaber von Mathematik und Elfenbeintürmen.
Roadmap
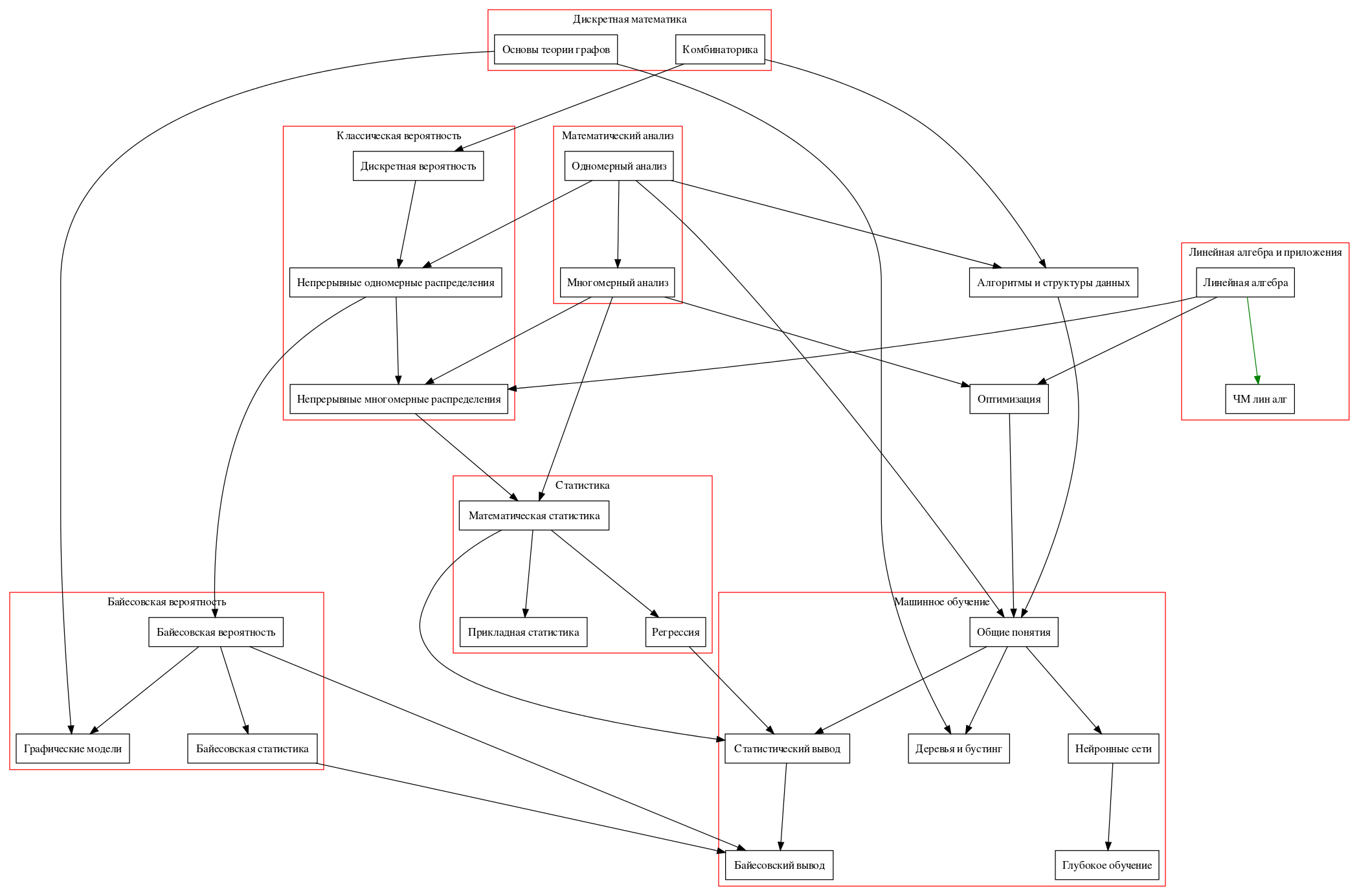
Ich werde tatsächlich zu bestimmten Kursen übergehen.
Analyse, er ist Kalkül
Interessanterweise wird er an russischen Universitäten unterrichtet: Die meisten von ihnen erinnern sich einige Jahre nach Ende des Kurses nur vage an einige Integrale, und etwas anderes scheint zu sein. Und dies trotz der Tatsache, dass die Analyse eine Disziplin ist, die tatsächlich zu den Grundlagen der Mathematik im Allgemeinen gehört. In der Regel gibt es keine Brücken von der Theorie zur Praxis, und dieser Kurs schwebt wie eine fliegende Insel irgendwo im Kopf, völlig getrennt vom wirklichen Leben. Es ist notwendig, dies zu überwinden, indem Probleme gelöst werden, die nicht nur aus dem Bereich der Mathematik, sondern auch aus dem „realen Leben“ wünschenswert sind.
Was müssen Sie aus der Analyse wissen?
Die wichtigsten Dinge, die wir brauchen werden, sind die Konzepte von Grenze, Kontinuität, Ableitung, Funktion vieler Variablen, Gradient, Integral, Integral mit variabler Obergrenze, mehrdimensionales Integral *.
Literatur
Bring it on : Hier ist alles mehr oder weniger Standard -
Piskunov / Fichtenholtz .
Tut mir sehr weh :
Zorich, Band 1 . Ich liebe dieses Buch sehr, sehr; Dies ist kein Lehrbuch, sondern ein Roman in Formeln, so etwas wie Eugene Onegin. Leider ist es komplizierter als Standard-Analysekurse, da viele Dinge allgemeiner gegeben werden und Sie sich daran gewöhnen müssen. Aufgrund dieser Gemeinsamkeit sind jedoch viele unterschiedliche Dinge miteinander verbunden (siehe die gleichen Grenzen auf der Basis).
Albtraum :
Zorich Band 1 + Band 2, Rudin „Grundlagen der mathematischen Analyse“, Lemberg „Vorlesungen zur mathematischen Analyse“, Ramanan „Global Calculus“.Im Allgemeinen lautet die Zusammenfassung hier: Die Analyseliteratur, auch in russischer Sprache, ist voll; Lehrbücher sind in der Regel rein mathematisch. Als Ergänzung zu Lehrbüchern der Stufe 2-3 kann ich verschiedene Kurse empfehlen:
Ich habe mir die Kurse aus dem MIPT-Hörsaal zur Analyse nicht angesehen, aber der Vollständigkeit halber werde ich auch Folgendes geben:
Übe
Das Üben und Anwenden des erworbenen Wissens ist nicht nur „optional“, sondern streng obligatorisch, da sonst die gesamte Theorie mit einem toten Gewicht an Ihnen hängt und Sie schnell auf den Grund sinken, ohne es zu merken.
Ich schlage vor, die folgenden Optionen in Betracht zu ziehen:
Demidovich, Problemstellungen aus den MIT-Kursen (https://ocw.mit.edu/courses/mathematics/18-01sc-single-variable-calculus-fall-2010/index.htm)
Lineare Algebra
Tägliches Brot für Data Science und für die Wissenschaft im Allgemeinen. Leider haben die Menschen gelernt, nur lineare Gleichungen und ihre Systeme gut zu lösen. Für Gleichungen ab Grad 2 gibt es alle möglichen sehr nicht trivialen Theorien (kommutative Algebra, algebraische Geometrie und ähnliche). Daher werden bei der Analyse von Daten hauptsächlich lineare Modelle verwendet (oder verallgemeinerte lineare Modelle wie logistische Regressionen, Perzeptrone usw.).
Es gibt viele Bücher über lineare Algebra auf Russisch. Das Problem ist, dass sie entweder für Mathematiker geschrieben sind oder deprimierend viele Indizes enthalten (und hinter den Bäumen kein Wald sichtbar ist). Oft liegt der Schwerpunkt in Universitätskursen auf der jordanischen Form; andere Standardformen werden oft nicht erwähnt; Es gibt Gauß und dummen Kramer, aber selten, was mit LU passiert, mit SVD.
Was müssen Sie aus der linearen Algebra wissen?
Das Konzept von Vektor und Vektorraum; das Konzept eines linearen Operators; Kommunikation von Operatoren und Matrizen; Matrixzerlegungen (mindestens LU, SVD); Eigenvektoren und Eigenwerte; orthogonale, einheitliche Operatoren; symmetrische und hermitische Operatoren; quadratische Formen, Reduktion auf die Hauptachsen.
Literatur
Bring it on :
Gilbert Strangs OCW-MIT-Kurs über lineare Algebra + sein Buch .
ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/index.htmDas Beste an diesem Kurs ist das Fehlen von „komplexen“ und ziemlich dummen Theoremen der linearen Algebra, allen Arten von dualen Räumen, einer Vielzahl von Problemen im Buch, einem praxisorientierten Ansatz (nicht „was ist das“, sondern „wie man es berechnet“). Weitere Erklärungskurse in linearer Algebra habe ich noch nicht getroffen.
Tut mir sehr weh :
Axler „Lineare Algebra richtig gemacht“; Gelfand "Vorlesungen zur linearen Algebra "; MIPT-Kurs
lectoriy.mipt.ru/course/LinearAlgebra ;
Kostrikin „Einführung in die Algebra, Teil 2“, Tyrtyshnikov „Matrixanalyse und lineare Algebra“.Das Problem bei Büchern und Kursen dieser Komplexität ist, dass sie theoretisch orientiert sind. Es gibt lineare Funktionale und duale Räume, aber es gibt keine Projektionsmatrix auf dem Unterraum und praktische Methoden zur Berechnung von Eigenwerten. Kurse dieser Stufe müssen höchstwahrscheinlich durch starke Übung ergänzt werden. zum Beispiel durch numerische Methoden der linearen Algebra.
Über das letzte Buch separat. Meiner Meinung nach ist dies eines der erfolgreichsten russischsprachigen Bücher über lineare Algebra in dem Sinne, dass es nicht sehr von der Praxis getrennt ist. Gleichzeitig enthält es alle Arten von "fortgeschrittenen" Themen. Bis zu einem gewissen Grad kann es Strangs Vorlesungen vollständig ersetzen, aber es muss durch einfache Aufgaben ergänzt werden, um „Ihre Hand zu füllen“. Es gibt Probleme in diesem Buch, aber sie sind ziemlich schwerwiegend.
Albtraum :
Kostrikin-Manin „Lineare Algebra und Geometrie“, Shafarevich-Remizov „Lineare Algebra und Geometrie“.Im Allgemeinen gibt es viel gute russische Literatur, insbesondere auf der letzten Ebene, aber sie leidet unter übermäßiger Komplexität.
Übe
Wie im ersten Fall ist Übung erforderlich. Go SVD - Lernen Sie die Bildkomprimierung. Gehen Sie Matrixmultiplikationen durch - lernen Sie die schnelle Fourier-Transformation, den Strassen-Algorithmus; viele Probleme lösen (zum Beispiel aus den
Problembüchern von Kostrikin oder Proskuryakov ); Schreiben Sie Ihre LU-Zerlegung, Gauß. Für die Beständigsten kann ich wunderbare Bücher über numerische Methoden der linearen Algebra anbieten, wie
Trefethen, Bau "NUMERICAL LINEAR ALGEBRA"; Horn, Johnson "Matrix Analysis" . Diese Bücher werden zuallererst nützlich sein, um Ihre Hände zu „stopfen“; zweitens wird sofort klar, dass viele theoretische Methoden über die Prosa des Lebens (Maschinengenauigkeit, Instabilität der Methoden, Arbeiten mit spärlichen Matrizen) in Chips zerlegt werden.
Diskrete Mathematik
Ein weiterer Wal der modernen CS. Hier interessieren uns vor allem die Kombinatorik und die Grundlagen der Graphentheorie.
Was müssen Sie aus der Kombinatorik und Graphentheorie wissen?
Binomialkoeffizienten, ihre Asymptotik; Grafiken; Bäume; Tiefen- und Breitensuche; Wiederholungsbeziehungen und ihre Lösungen;
Literatur
Bring it on :
Anderson J. "Diskrete Mathematik und Kombinatorik"; Haggarti, Schlipf J., Whitesides S. "Diskrete Mathematik für Programmierer", Ore O. "Graphen und ihre Anwendung .
"Die ersten beiden Bücher - exzellente Talmuds in diskreter Mathematik - decken fast alle Fragen ab, die Sie wissen müssen.
Tut mir sehr weh :
Graham, Knut, Patashnik "Konkrete Mathematik", Harari "Graphentheorie", Erz "Graphentheorie".Albtraum :
Sachkov „Einführung in kombinatorische Methoden der diskreten Mathematik“, Omelchenko „Graphentheorie“.Übe
In Lehrbüchern zur Kombinatorik sind in der Regel zahlreiche Probleme enthalten; sie müssen gelöst werden. Tatsächlich ist jede Kombinatorik die Kunst, verschiedene Probleme zu lösen, und nicht nur eine einzige Theorie.