Amateur-Mathematiker entdeckte die kleinste universelle Abdeckung

Durch schwierige geometrische Berechnungen entdeckte Philip Gibbs die kleinste bekannte Beschichtung für jede mögliche Form.

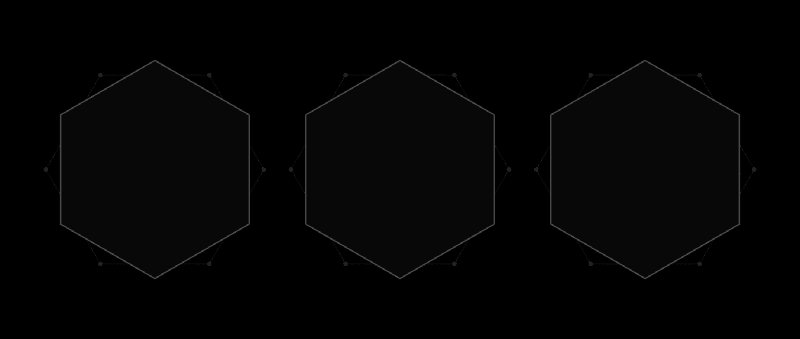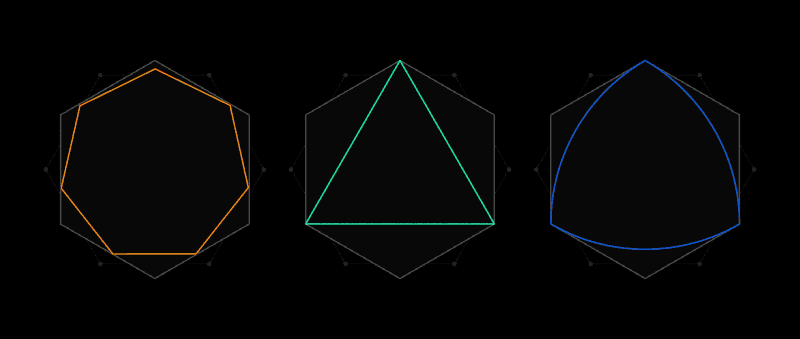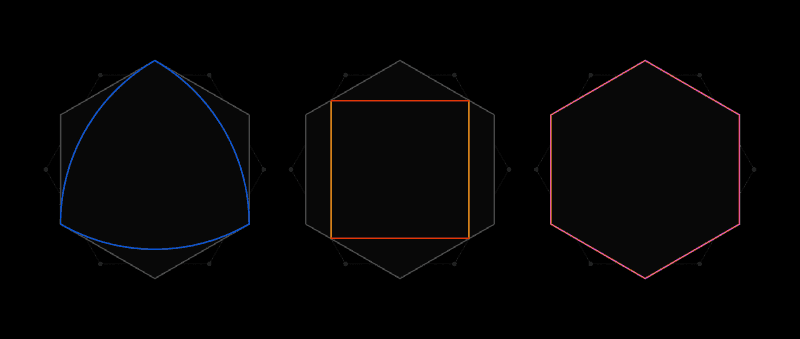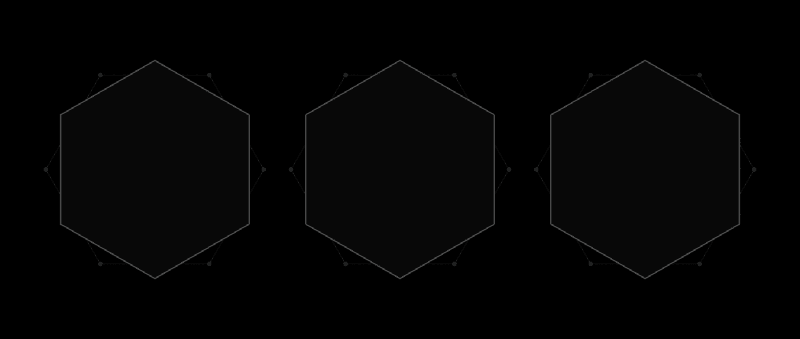Eine universelle Abdeckung wie ein Sechseck kann um jede Form beschrieben werden.

Philip Gibbs ist kein professioneller Mathematiker. Als er über eine Aufgabe nachdenken wollte, suchte er nach einer, die ein Amateur bewältigen konnte. Er entdeckte eine schwierige Aufgabe, die selbst die besten Köpfe verrückt machen kann. Und in einem in diesem Jahr veröffentlichten Artikel hat Gibbs bedeutende Fortschritte bei der Lösung der Frage vor hundert Jahren erzielt, abhängig von der Fähigkeit, die Fläche bis auf atomare Skalen genau zu messen.

Der erste , der dieses Problem vorschlug , war der französische Mathematiker Henri Leon Lebesgue in einem Brief an seinen Freund Julius Pal aus dem Jahr 1914. Lebesgue fragte: Wie ist die Form des kleinstmöglichen Bereichs, der eine große Anzahl anderer Formen vollständig abdecken kann (mit einer gemeinsamen Eigenschaft, die unten beschrieben wird)?

Im letzten Jahrhundert hat sich die Aufgabe, eine universelle Abdeckung zu finden, in eine Mausefalle verwandelt: Die Fortschritte bei der Lösung waren, wenn sie regelmäßig stattfanden, immer erstaunlich gering. Gibbs 'Verbesserung ist dramatisch geworden - obwohl Sie noch ein bisschen darüber nachdenken müssen.

Stellen Sie sich ein Dutzend Papierausschnitte in verschiedenen Größen und Formen vor, die auf Ihrem Boden liegen. Stellen Sie sich nun vor, Ihnen wird angeboten, eine weitere Form zu entwickeln, die groß genug ist, um eine der verfügbaren Formen abzudecken. Durch Experimentieren - indem Sie Formen überlagern und umdrehen - können Sie einen Weg finden, um dieses Problem zu lösen. Aber können Sie nach einer universellen Abdeckung sicher sein, dass Sie die kleinste gefunden haben? Sie können sich vorstellen, dass Sie tagsüber regelmäßig zu Ihrem Formular zurückkehren und hier und da die Möglichkeit finden, zusätzliche Teile abzuschneiden.

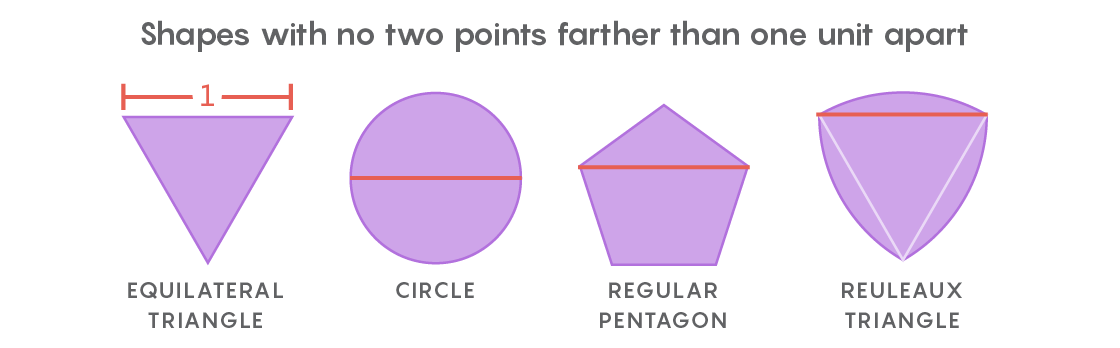
Dies ist der Geist des Lebesgue-Problems der universellen Abdeckung. Anstelle von Papierausschnitten werden Formen berücksichtigt, bei denen zwei beliebige Punkte nicht weiter als eine Längeneinheit voneinander entfernt sind. Die offensichtlichste Form ist ein Kreis mit einem Durchmesser von 1, aber es gibt unendlich viele davon: ein gleichseitiges Dreieck, ein regelmäßiges Fünfeck, ein regelmäßiges Sechseck, eine dreieckige Form mit geschwollenen Seiten, bekannt als Röhlo-Dreieck - und dies ist nur für den Anfang. Die Vielfalt der Formen macht es schwierig, für alle die kleinste Abdeckung zu finden.



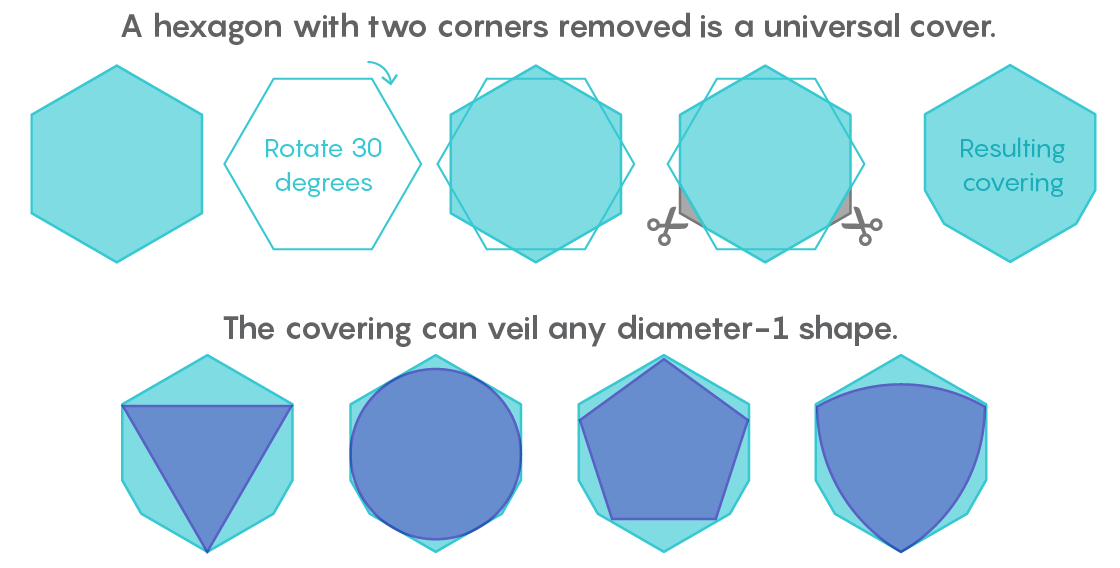
Kurz nachdem Pal einen Brief von Lebesgue erhalten hatte, erkannte er, dass das reguläre Sechseck die universelle Abdeckung sein würde. Und dann verbesserte er dieses Ergebnis, indem er feststellte, dass durch Schneiden von zwei Ecken des Sechsecks, die nicht nebeneinander stehen, eine Form mit kleinerem Bereich erhalten werden kann, die sich immer noch als universelle Beschichtung herausstellt.

„Nimm ein Sechseck, lege ein zweites darauf, drehe es um 30 Grad und schneide zwei Ecken ab. Hier hat Pal die Recherche abgeschlossen “, sagte Gibbs.

In den nächsten 80 Jahren schnitten zwei andere Mathematiker schmale Streifen von Pal's Universalabdeckung ab. 1936 entfernte Roland Sprag ein kleines Stück neben einer der Ecken. 1992 wird Hansen zwei Miniaturkeile aus der unteren rechten und linken Ecke entfernen. Hansens Illustrationen könnten die Position dieser Teile wiedergeben, aber nicht ihre Größe: Ihre Fläche betrug 0,00000000004 Einheiten.



"Man kann sie nicht auf einer Skala zeichnen, sie hätten die Größe eines Atoms", sagte John Baez , Mathematiker an der University of California in Riverside.

Baez nahm Lebesgues Aufgabe aus der Vergessenheit, als er 2013 in seinem Blog über populäre Mathematik darüber schrieb . Er gab zu, dass er von dieser Aufgabe so fasziniert war, dass ein Video mit einem ertrinkenden Insekt Sie faszinieren könnte. "Mein Interesse an der Aufgabe war ungesund", schrieb BAez. "Ich weiß nicht, warum es wichtig sein könnte." Ich sehe nicht, wie es sich mit vielen anderen wunderbaren Aufgaben verbinden kann. Es scheint einfach unglaublich komplex im Vergleich zum ersten Eindruck. Ich bewundere die Leute, die daran arbeiten, genauso wie die Leute, die beschließen, die Antarktis mit Skiern zu durchqueren. “

Philip Gibbs hat die Antarktis nie mit Skiern überquert, sondern den Baez-Blog gelesen. Als er eine Aufzeichnung von Lebesgues Problem traf, dachte er: "Nun, genau das brauche ich."

Atomschere

Gibbs dachte einmal, er könnte Wissenschaftler werden. Er erhielt ein Diplom in Mathematik von der University of Cambridge und einen Doktortitel in theoretischer Physik von der University of Glasgow. Er verlor jedoch bald seine Begeisterung für akademische Forschung und wurde Programmierer. Er arbeitete an Systemen für Schiffsdesign, Flugverkehrsmanagement und Finanzen und ging 2006 in den Ruhestand.

Gibbs interessierte sich weiterhin für akademische Angelegenheiten, aber als Laienforscher konnte er wenig tun. "Für einen unabhängigen Wissenschaftler ist es schwierig, den Überblick zu behalten", sagte er. "Aber wenn Sie die richtige Nische finden, können Sie etwas tun und nützliche Ergebnisse erzielen."


Amateur Mathematiker Philip Gibbs

Eine solche Nische war das Problem der universellen Abdeckung in Lebesgue. Diese Aufgabe erhielt nie die Aufmerksamkeit von Mathematikern, so dass er vermutete, dass er einige Fortschritte erzielen könnte. Gibbs erkannte auch, dass seine Programmiererfahrung von Vorteil sein könnte. "Ich suche immer nach Problemen, bei denen Computer und experimentelle Mathematik verwendet werden können", sagte er.

Im Jahr 2014 führte Gibbs eine Computersimulation für 200 zufällige Formen des Durchmessers 1 durch. Aus den Simulationen ging hervor, dass er möglicherweise ein kleines Stück aus der oberen Ecke der vorherigen kleinsten Abdeckung schneiden konnte. Er verwandelte dies in einen Beweis dafür, dass die neue Beschichtung für alle möglichen Formen von Durchmesser 1 geeignet ist. Gibbs schickte den Beweis an Baez, der zusammen mit einer seiner Schülerinnen, Karina Baghdasaryan, Gibbs half, der Arbeit einen formalen mathematischen Stil zu verleihen.

Die drei veröffentlichten ihre Arbeiten im Februar 2015 im Internet. Dadurch wurde der Bereich der kleinstmöglichen universellen Abdeckung von 0,8441377 auf 0,8441153 Einheiten reduziert. Die Einsparungen von 0,0000224 Einheiten waren fast eine Million Mal höher als die von Hansen im Jahr 1992.

Gibbs war zuversichtlich, dass er das Ergebnis verbessern konnte. In einer im Oktober veröffentlichten Arbeit schnitt er ein weiteres relativ großes Stück von einer Universalbeschichtung ab und brachte seine Fläche auf 0,84409359 Einheiten.



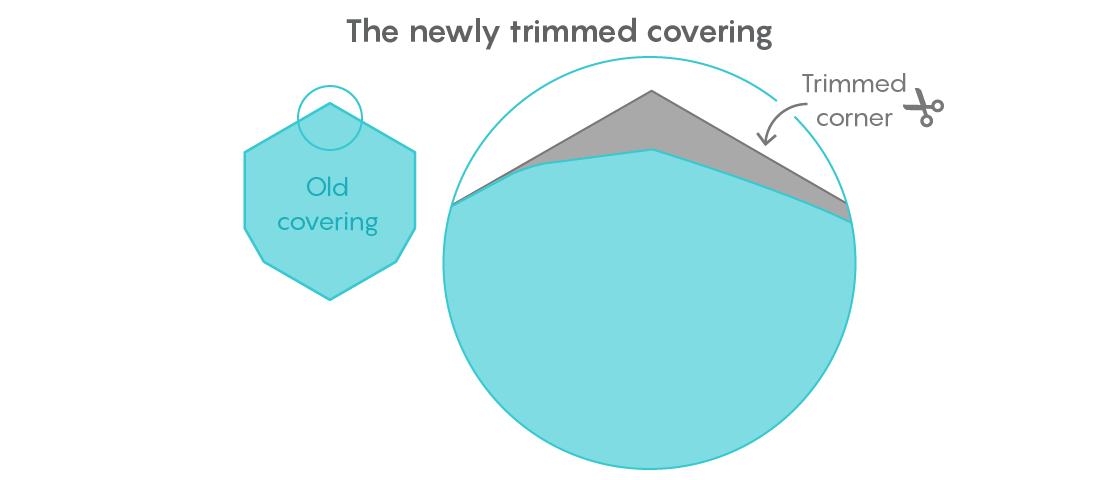
Seine Strategie bestand darin, alle Formen mit einem Durchmesser von 1 in die Ecke der Universalbeschichtung zu verschieben, die er vor einigen Jahren entdeckt hatte, und dann den gesamten verbleibenden Bereich der gegenüberliegenden Ecke zu entfernen. Eine genaue Messung des eingesparten Platzes hat sich jedoch als schwierig erwiesen. Die von Gibbs verwendeten Techniken basierten auf der euklidischen Geometrie, wurden jedoch mit einer solchen Präzision durchgeführt, dass jeder Schüler schockiert würde.

„Aus mathematischer Sicht ist das alles Geometrie für die High School. Aber mit fanatischer Spannung aufgeführt “, schrieb Baez.

Bisher hält Gibbs den ersten Platz auf der Suche nach der kleinsten universellen Berichterstattung, aber sein Preis ist in Gefahr. Gibbs glaubt, dass es eine Möglichkeit gibt, die Abdeckung noch kleiner zu finden. Baez hofft, dass die Aufmerksamkeit, die Gibbs dem Lebesgue-Problem widmete, das Interesse anderer Mathematiker weckt. Vielleicht ist es an der Zeit, das Lineal und den Kompass beiseite zu lassen und das gesamte Arsenal der modernen Mathematik zu nutzen.

"Es ist möglich, dass der richtige Weg, um dieses Rätsel zu lösen, völlig andere Ideen verwendet", sagte er, "obwohl ich keine Ahnung habe, welche Ideen dies sein könnten."