Perspektive: MultiClet S1

Es ist also Zeit, über die nächste Generation mehrzelliger Prozessoren zu sprechen: MultiClet S1. Wenn Sie zum ersten Mal davon hören, lesen Sie unbedingt die Geschichte und Ideologie der Architektur in diesen Artikeln:

• "Ein mehrzelliger Prozessor ist was?"
• "Multiclet R1 - die ersten Tests"
• "LLVM-basierter C / C ++ - Compiler für mehrzellige Prozessoren: sein oder nicht sein?"

Im Moment befindet sich der neue Prozessor in der Entwicklung, aber die ersten Ergebnisse sind bereits erschienen und Sie können bewerten, wozu er in der Lage sein wird.

Beginnen wir mit den größten Änderungen: Grundfunktionen.

Eigenschaften

Folgende Indikatoren sollen erreicht werden:

1. Anzahl der Zellen: 64
2. Technischer Prozess: 28 nm
3. Taktfrequenz: 1,6 GHz
4. Die Größe des Speichers auf dem Chip: 8 MB
5. Kristallfläche: 40 mm ²
6. Leistungsaufnahme: 6 W.

Die tatsächlichen Zahlen werden auf der Grundlage der Ergebnisse der Tests der hergestellten Muster im Jahr 2019 bekannt gegeben. Zusätzlich zu den Eigenschaften des Chips selbst unterstützt der Prozessor bis zu 16 GB DDR4 3200 MHz Standard-RAM, PCI Express-Bus und PLL.

Es sollte beachtet werden, dass der 28-nm-Herstellungsprozess der niedrigste Haushaltsbereich ist, für dessen Verwendung keine besonderen Berechtigungen erforderlich sind. Daher wurde er ausgewählt. Durch die Anzahl der Zellen wurden verschiedene Optionen in Betracht gezogen: 128 und 256, aber mit zunehmender Fläche des Kristalls nimmt der Prozentsatz der Ausschussprodukte zu. Wir haben uns auf 64 Zellen und dementsprechend auf eine relativ kleine Fläche niedergelassen, was eine größere Ausbeute an geeigneten Kristallen auf der Platte ergibt. Eine Weiterentwicklung ist im Rahmen des ICS (System im Fall) möglich , wo es möglich sein wird, mehrere 64-Zell-Kristalle in einem Fall zu kombinieren.

Es muss gesagt werden, dass sich der Zweck und die Verwendung des Prozessors radikal ändern. S1 wird kein Mikroprozessor sein, der wie P1 und R1 zum Einbetten ausgelegt ist, sondern ein Beschleuniger für Berechnungen. Genau wie bei der GPGPU kann eine S1-basierte Karte in die PCI Express-Hauptplatine eines normalen PCs eingesetzt und für die Datenverarbeitung verwendet werden.

Architektur

In S1 ist die "Mehrfachzelle" jetzt die minimale Recheneinheit: ein Satz von 4 Zellen, die eine bestimmte Folge von Befehlen ausführen. Zunächst war geplant, Multizellen zu Gruppen zu kombinieren, die als Cluster für die gemeinsame Ausführung von Befehlen bezeichnet werden: Ein Cluster musste 4 Multizellen enthalten, insgesamt befanden sich 4 separate Cluster auf einem Kristall. Jede Zelle hat jedoch eine vollständige Verbindung mit allen anderen Zellen im Cluster, und mit einer Zunahme der Bindungsgruppe wird sie zu stark, was das topologische Design der Mikroschaltung erheblich kompliziert und ihre Eigenschaften verringert. Daher beschlossen sie, die Clusterteilung aufzugeben, da Komplikationen die Ergebnisse nicht rechtfertigen. Darüber hinaus ist es für maximale Leistung am vorteilhaftesten, Code auf jeder Multizelle parallel auszuführen. Insgesamt enthält der Prozessor jetzt 16 separate Mehrzellen.

Eine Mehrzelle, obwohl sie aus 4 Zellen besteht, unterscheidet sich von einer 4-Zellen-R1, in der jede Zelle ihren eigenen Speicher, ihren eigenen Block von Beispielbefehlen und ihre eigene ALU hatte. S1 ist etwas anders angeordnet. ALU besteht aus 2 Teilen: einem Gleitkomma-Arithmetikblock und einem Ganzzahl-Arithmetikblock. Jede Zelle hat einen separaten ganzzahligen Block, aber es gibt nur zwei Blöcke mit einem Gleitkomma in einer Mehrzelle, und daher teilen zwei Zellenpaare sie unter sich auf. Dies geschah hauptsächlich, um die Fläche des Kristalls zu verkleinern: Die 64-Bit-Gleitkomma-Arithmetik nimmt im Gegensatz zur Ganzzahl-Arithmetik viel Platz ein. Eine solche ALU in jeder Zelle zu haben, stellte sich als redundant heraus: Durch das Abrufen von Befehlen wird keine ALU geladen, und sie sind inaktiv. Während die Anzahl der ALU-Blöcke reduziert und das Tempo beim Abrufen von Befehlen und Daten beibehalten wird, ändert sich, wie die Praxis gezeigt hat, die Gesamtzeit zum Lösen von Problemen praktisch nicht oder nur geringfügig, und ALU-Blöcke sind vollständig geladen. Außerdem wird Gleitkomma-Arithmetik nicht so oft verwendet wie bei Ganzzahlen.

Eine schematische Ansicht der Prozessorblöcke R1 und S1 ist in der folgenden Abbildung dargestellt. Hier:

• CU (Control Unit) - Befehlsabrufeinheit
• ALU _FX - arithmetische Logikeinheit der Ganzzahlarithmetik
• ALU _FP - Arithmetische Logikeinheit der Gleitkomma-Arithmetik
• DMS (Data Memory Scheduler) - Datenspeicher-Steuereinheit
• DM - Datenspeicher
• PMS (Program Memory Scheduler) - Programmspeichersteuergerät
• PM - Programmspeicher

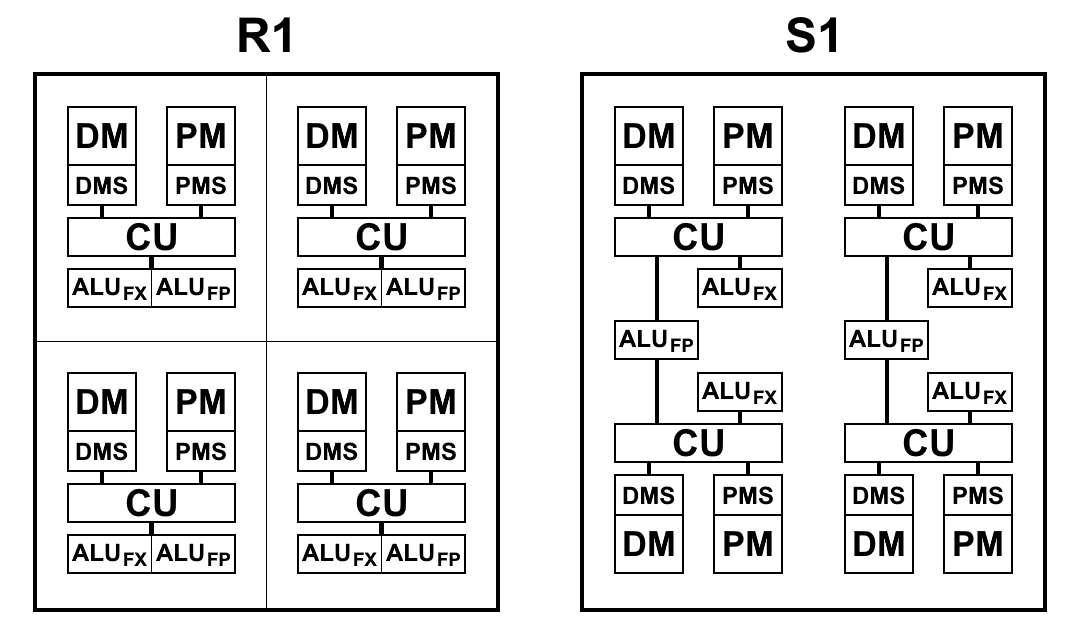
Architektonische Unterschiede S1:

1. Teams können jetzt auf Teamergebnisse aus vorherigen Absätzen zugreifen. Dies ist eine sehr wichtige Änderung, mit der Sie die Übergänge beim Verzweigen des Codes erheblich beschleunigen können. Die Prozessoren P1 und R1 hatten keine andere Wahl, als die gewünschten Ergebnisse in den Speicher zu schreiben und sie sofort mit den ersten Befehlen im neuen Absatz zurückzulesen. Selbst wenn Speicher auf einem Chip verwendet wird, dauern Schreib- und Lesevorgänge jeweils 2 bis 5 Zyklen, die durch einfaches Verweisen auf das Ergebnis des Befehls aus dem vorherigen Absatz gespeichert werden können
2. Das Schreiben in den Speicher und in die Register erfolgt jetzt sofort und nicht mehr am Ende eines Absatzes, sodass Sie vor dem Ende des Absatzes mit dem Schreiben von Befehlen beginnen können. Dadurch wird die potenzielle Ausfallzeit zwischen Absätzen reduziert.
3. Das Befehlssystem wurde optimiert, nämlich:
   
   • 64-Bit-Ganzzahlarithmetik hinzugefügt: Addition, Subtraktion, Multiplikation von 32-Bit-Zahlen, wodurch ein 64-Bit-Ergebnis zurückgegeben wird.
   • Die Methode zum Lesen aus dem Speicher wurde geändert: Jetzt können Sie für jeden Befehl einfach die Adresse angeben, von der Sie Daten als Argument lesen möchten, während die Reihenfolge der Lese- und Schreibbefehle beibehalten wird.
     
     Außerdem wurde ein separater Speicherlesebefehl überflüssig. Stattdessen wird der Befehl load value im Ladeschalter verwendet (zuvor get ), wobei die Adresse im Speicher als Argument angegeben wird:
     
     

     .data foo: .long 0x1234 .text habr: load_l foo ;      foo load_l [foo] ;    0x1234 add_l [foo], 0xABCD ;       ;   complete 

     
     
   • Es wurde ein Befehlsformat hinzugefügt, das die Verwendung von 2 konstanten Argumenten ermöglicht.
     Bisher konnten Sie eine Konstante nur als zweites Argument angeben. Das erste Argument sollte immer eine Verknüpfung zum Ergebnis im Switch sein. Die Änderung gilt für alle Teams mit zwei Argumenten. Das Konstantenfeld ist immer 32 Bit, so dass dieses Format beispielsweise das Generieren von 64-Bit-Konstanten mit einem Befehl ermöglicht.
     
     Es war:
     
     

      load_l 0x12345678 patch_q @1, 0xDEADBEEF 

     
     Es wurde:
     
     

      patch_q 0x12345678, 0xDEADBEEF 

     
     
   • Geänderte und ergänzte Vektordatentypen.
     Was früher als "gepackte" Datentypen bezeichnet wurde, kann jetzt sicher als vektoriell bezeichnet werden. In P1 und R1 nahmen Operationen an gepackten Zahlen nur eine Konstante als zweites Argument an, d. H. Zum Beispiel wurde beim Hinzufügen jedes Element des Vektors mit derselben Zahl hinzugefügt, und dies konnte nicht intelligent angewendet werden. Nun können ähnliche Operationen auf zwei vollständige Vektoren angewendet werden. Darüber hinaus stimmt diese Art der Arbeit mit Vektoren vollständig mit dem Mechanismus der Vektoren in LLVM überein, der es dem Compiler nun ermöglicht, Code unter Verwendung von Vektortypen zu generieren.
     
     

      patch_q 0x00010002, 0x00030004 patch_q 0x00020003, 0x00040005 mul_ps @1, @2 ;  - 00020006000C0014 

     
     
   
   
4. Prozessorflags entfernt.
   
   Infolgedessen wurden ungefähr 40 Teams entfernt, die ausschließlich auf den Werten der Flaggen basierten. Dies hat die Anzahl der Teams und dementsprechend die Fläche des Kristalls erheblich reduziert. Und alle notwendigen Informationen werden jetzt direkt in der Schaltzelle gespeichert.
   
   
   • Beim Vergleich mit Null wird anstelle des Null-Flags nur noch der Wert im Schalter verwendet
   • Anstelle des Vorzeichen-Flags wird jetzt ein Bit verwendet, das dem Befehlstyp entspricht: 7. für Byte, 15. für kurz, 31. für lang, 63. für Quad. Aufgrund der Tatsache, dass das Zeichen unabhängig vom Typ bis zum 63. Bit multipliziert wird, können Sie Zahlen verschiedener Typen vergleichen:
     
     

      .data long: .long -0x1000 byte: .byte -0x10 .text habr: a := load_b [byte] ;     0xFFFFFFFFFFFFFFF0, ;   byte 7    63. b := loadu_b [byte] ;     0x00000000000000F0, ; ..  loadu_b    c := load_l [long] ;     0xFFFFFFFFFFFFF000. ge_l @a, @c ;   "  "  1: ;   31 ,   . lt_s @a, @b ; 1, .. b     complete 

     
     
   • Das Übertragsflag wird nicht mehr benötigt, da es eine 64-Bit-Arithmetik gibt
   
   
5. Die Übergangszeit von Absatz zu Absatz wurde auf 1 Takt reduziert (anstelle von 2-3 in R1).

LLVM-basierter Compiler

Der C-Sprach-Compiler für S1 ähnelt R1, und da sich die Architektur nicht grundlegend geändert hat, sind die im vorherigen Artikel beschriebenen Probleme leider nicht verschwunden.

Bei der Implementierung des neuen Befehlssystems verringerte sich jedoch die Menge des Ausgabecodes von selbst, einfach aufgrund der Aktualisierung des Befehlssystems. Darüber hinaus gibt es viele weitere kleinere Optimierungen, die die Anzahl der Befehle im Code verringern, von denen einige bereits ausgeführt wurden (z. B. Generieren von 64-Bit-Konstanten mit einem einzigen Befehl). Es müssen jedoch noch ernsthaftere Optimierungen vorgenommen werden, die in aufsteigender Reihenfolge sowohl hinsichtlich der Effizienz als auch der Komplexität der Implementierung erstellt werden können:

1. Die Fähigkeit, alle Befehle mit zwei Argumenten mit zwei Konstanten zu generieren.
   
   Das Generieren einer 64-Bit-Konstante über patch_q ist nur ein Sonderfall, aber wir brauchen einen allgemeinen. Tatsächlich besteht der Zweck dieser Optimierung darin, den Teams zu ermöglichen, nur das erste Argument als Konstante zu ersetzen, da das zweite Argument immer eine Konstante sein kann, und dies ist seit langem implementiert. Dies ist kein sehr häufiger Fall, aber wenn Sie beispielsweise eine Funktion aufrufen und die Rücksprungadresse von dort oben in den Stapel schreiben müssen, können Sie dies tun
   
   

    load_l func wr_l @1, #SP 

   
   optimieren auf
   
   

    wr_l func, #SP 

   
   
2. Die Möglichkeit, den Speicherzugriff durch ein Argument in einem beliebigen Befehl zu ersetzen.
   Wenn Sie beispielsweise zwei Zahlen aus dem Speicher hinzufügen müssen, können Sie dies tun
   
   

    load_l [foo] load_l [bar] add_l @1, @2 

   
   optimieren auf
   
   

    add_l [foo], [bar] 

   
   Diese Optimierung ist eine Erweiterung der vorherigen, hier ist jedoch bereits eine Analyse erforderlich: Ein solcher Austausch kann nur durchgeführt werden, wenn die geladenen Werte in diesem Additionsbefehl nur einmal und nirgendwo anders verwendet werden. Wenn das Leseergebnis auch nur in zwei Befehlen verwendet wird, ist es rentabler, einmal als separaten Befehl aus dem Speicher zu lesen und in den anderen beiden über den Schalter darauf zu verweisen.
   
3. Optimierung der Übertragung virtueller Register zwischen Basiseinheiten.
   Für R1 erfolgte die Übertragung aller virtuellen Register über den Speicher, was zu einer sehr großen Anzahl von Lese- und Schreibvorgängen im Speicher führt, aber es gab einfach keine andere Möglichkeit, Daten zwischen Absätzen zu übertragen. Mit S1 können Sie auf die Ergebnisse der Befehle der vorherigen Absätze zugreifen. Daher können theoretisch viele Speicheroperationen entfernt werden, was den größten Effekt unter allen Optimierungen erzielen würde. Dieser Ansatz ist jedoch immer noch durch den Wechsel begrenzt: Es können bisher nicht mehr als 63 vorherige Ergebnisse von jeder Übertragung des virtuellen Registers auf diese Weise implementiert werden. Wie dies zu tun ist, ist keine triviale Aufgabe, und eine Analyse der Lösungsmöglichkeiten muss noch durchgeführt werden. Die Compilerquellen werden möglicherweise gemeinfrei angezeigt. Wenn also jemand Ideen hat und Sie sich an der Entwicklung beteiligen möchten, können Sie dies tun.
   

Benchmarks

Da der Prozessor noch nicht auf dem Chip freigegeben wurde, ist es schwierig, seine tatsächliche Leistung zu beurteilen. Der RTL-Kernel-Code ist jedoch bereits bereit, sodass Sie eine Bewertung mithilfe von Simulation oder FPGA vornehmen können. Um die folgenden Benchmarks auszuführen, haben wir eine Simulation mit dem ModelSim-Programm verwendet, um die genaue Ausführungszeit (in Maßen) zu berechnen. Da es schwierig ist, den gesamten Kristall zu simulieren, und dies sehr lange dauert, wurde eine Mehrfachzelle simuliert und das Ergebnis mit 16 multipliziert (wenn die Aufgabe für Multithreading ausgelegt ist), da jede Mehrfachzelle völlig unabhängig von den anderen arbeiten kann.

Gleichzeitig wurde auf Xilinx Virtex-6 eine Mehrzellenmodellierung durchgeführt, um die Leistung von Prozessorcode auf realer Hardware zu testen.

Coremark

CoreMark - eine Reihe von Tests zur umfassenden Bewertung der Leistung von Mikrocontrollern und Zentralprozessoren sowie deren C-Compilern. Wie Sie sehen können, ist der S1-Prozessor weder der eine noch der andere. Es ist jedoch beabsichtigt, absolut Arbitrierungscode auszuführen, d.h. Jeder, der auf dem Zentralprozessor ausgeführt werden könnte. CoreMark eignet sich also zur Bewertung der Leistung von S1 nicht schlechter.

CoreMark enthält Arbeiten mit verknüpften Listen, Matrizen, einer Zustandsmaschine und einer CRC- Summenberechnung. Im Allgemeinen stellt sich heraus, dass der größte Teil des Codes streng sequentiell ist (wodurch die mehrzellige Hardware-Parallelität auf Stärke getestet wird) und viele Zweige aufweist, weshalb die Compiler-Funktionen eine wichtige Rolle für die endgültige Leistung spielen. Der kompilierte Code enthält einige kurze Absätze, und trotz der Tatsache, dass die Übergangsgeschwindigkeit zwischen ihnen zugenommen hat, umfasst die Verzweigung die Arbeit mit dem Speicher, die wir maximal vermeiden möchten.

CoreMark-Scorecard:

	Multiclet R1 (llvm-Compiler)	Multiclet S1 (llvm-Compiler)	Elbrus-4C (R500 / E)	Texas Inst. AM5728 ARM Cortex-A15	Baikal-t1	Intel Core i7 7700K
Baujahr	2015	2019	2014	2018	2016	2017
Taktfrequenz, MHz	100	1600	700	1500	1200	4500
CoreMark Gesamtpunktzahl	59	18356	1214	15789	13142	182128
Coremark / MHz	0,59	11.47	5.05	10.53	10,95	40,47

Das Ergebnis einer Mehrfachzelle ist 1147 oder 0,72 / MHz, was höher als das von R1 ist. Dies spricht für die Vorteile der Entwicklung einer mehrzelligen Architektur im neuen Prozessor.

Weizenstein

Schleifstein - eine Reihe von Tests zur Messung der Prozessorleistung bei der Arbeit mit Gleitkommazahlen. Hier ist die Situation viel besser: Der Code ist ebenfalls sequentiell, jedoch ohne große Anzahl von Zweigen und mit guter interner Parallelität.

Whetstone besteht aus vielen Modulen, mit denen Sie nicht nur das Gesamtergebnis, sondern auch die Leistung für jedes einzelne Modul messen können:

1. Array-Elemente
2. Array als Parameter
3. Bedingte Sprünge
4. Ganzzahlige Arithmetik
5. Trigonometrische Funktionen (tan, sin, cos)
6. Prozeduraufrufe
7. Array-Referenzen
8. Standardfunktionen (sqrt, exp, log)

Sie sind in Kategorien unterteilt: Die Module 1, 2 und 6 messen die Leistung von Gleitkommaoperationen (Zeilen MFLOPS1-3); Module 5 und 8 - mathematische Funktionen (COS MOPS, EXP MOPS); Module 4 und 7 - Ganzzahlarithmetik (FIXPT MOPS, EQUAL MOPS); Modul 3 - Bedingte Sprünge (IF MOPS). In der folgenden Tabelle ist die zweite Zeile von MWIPS ein allgemeiner Indikator.

Im Gegensatz zu CoreMark wird Whetstone auf einem Kern oder, wie in unserem Fall, auf einer Mehrzelle verglichen. Da die Anzahl der Kerne in verschiedenen Prozessoren sehr unterschiedlich ist, betrachten wir für die Reinheit des Experiments die Indikatoren pro Megahertz.

Wetzstein-Scorecard:

CPU	MultiClet R1	MultiClet S1	Core i7 4820K	ARM v8-A53
Frequenz, MHz	100	1600	3900	1300
MWIPS / MHz	0,311	0,343	0,887	0,642
MFLOPS1 / MHz	0,157	0,156	0,341	0,268
MFLOPS2 / MHz	0,153	0,111	0,308	0,241
MFLOPS3 / MHz	0,029	0,124	0,167	0,239
COS MOPS / MHz	0,018	0,008	0,023	0,028
EXP MOPS / MHz	0,008	0,005	0,014	0,004
FIXPT MOPS / MHz	0,714	0,116	0,998	1.197
WENN MOPS / MHz	0,081	0,196	1,504	1.436
GLEICHE MOPS / MHz	0,143	0,149	0,251	0,439

Whetstone enthält viel direktere Rechenoperationen als CoreMark (was sich im folgenden Code sehr bemerkbar macht). Daher ist es wichtig, sich hier daran zu erinnern: Die Anzahl der Gleitkomma-ALUs wird halbiert. Die Rechengeschwindigkeit wurde jedoch im Vergleich zu R1 fast nicht beeinflusst.

Einige Module passen sehr gut zu einer mehrzelligen Architektur. Zum Beispiel zählt Modul 2 viele Werte in einem Zyklus, und dank der vollständigen Unterstützung von Gleitkommazahlen mit doppelter Genauigkeit durch den Prozessor und den Compiler erhalten wir nach der Kompilierung große und schöne Absätze, die die Rechenfähigkeiten einer mehrzelligen Architektur wirklich offenbaren:

popcnt

Um die Eigenschaften der Architektur selbst (unabhängig vom Compiler) widerzuspiegeln, messen wir etwas, das in Assembler geschrieben wurde, unter Berücksichtigung aller Merkmale der Architektur. Zum Beispiel das Zählen von Einheitsbits in einer 512-Bit-Zahl (popcnt). Zur Verdeutlichung werden wir die Ergebnisse einer Mehrzelle nehmen, damit sie mit R1 verglichen werden können.

Vergleichstabelle, Anzahl der Taktzyklen pro 32-Bit-Berechnungszyklus:

Algorithmus	Multiclet r1	Multiclet S1 (eine Multizelle)
Bithacks	5.0	2,625

Hier wurden neue aktualisierte Vektoranweisungen verwendet, die es uns ermöglichten, die Anzahl der Anweisungen im Vergleich zu demselben in R1-Assembler implementierten Algorithmus zu halbieren. Die Arbeitsgeschwindigkeit erhöhte sich jeweils um fast das Zweifache.

Ethereum

Benchmarks sind natürlich gut, aber wir haben eine bestimmte Aufgabe: einen Berechnungsbeschleuniger zu erstellen, und es wäre schön zu wissen, wie er mit realen Aufgaben umgeht. Moderne Kryptowährungen eignen sich am besten für eine solche Überprüfung, da Mining-Algorithmen auf vielen verschiedenen Geräten ausgeführt werden und daher als Vergleichsmaßstab dienen können. Wir haben mit Ethereum und dem Ethash-Algorithmus begonnen, der direkt auf dem Mining-Gerät ausgeführt wird.

Ethereum wurde aus folgenden Gründen ausgewählt. Wie Sie wissen, werden Algorithmen wie Bitcoin von spezialisierten ASIC-Chips sehr effizient implementiert, sodass die Verwendung von Prozessoren oder Grafikkarten zum Mining von Bitcoin und seinen Klonen aufgrund der geringen Leistung und des hohen Stromverbrauchs wirtschaftlich nachteilig wird. Um dieser Situation zu entkommen, entwickelt die Bergarbeitergemeinschaft Kryptowährungen nach anderen algorithmischen Prinzipien, wobei der Schwerpunkt auf der Entwicklung von Algorithmen liegt, die Allzweckprozessoren oder Grafikkarten für das Bergbau verwenden. Dieser Trend dürfte sich auch in Zukunft fortsetzen. Ethereum ist die bekannteste Kryptowährung, die auf diesem Ansatz basiert. Das Hauptwerkzeug für den Abbau von Ethereum sind Grafikkarten, die in Bezug auf die Effizienz (Hashrate / TDP) den Mehrzweckprozessoren deutlich (mehrmals) voraus sind.

Ethash ist ein sogenannter speichergebundener Algorithmus, d.h. Die Berechnungszeit wird hauptsächlich durch die Größe und Geschwindigkeit des Speichers und nicht durch die Geschwindigkeit der Berechnungen selbst begrenzt. Für das Ethereum-Mining sind Grafikkarten am besten geeignet, aber ihre Fähigkeit, viele Vorgänge gleichzeitig auszuführen, hilft nicht viel, und sie beruhen immer noch auf der Geschwindigkeit des Arbeitsspeichers, die in diesem Artikel deutlich gezeigt wird. Von dort aus können Sie ein Bild aufnehmen, das die Funktionsweise des Algorithmus veranschaulicht, um zu erklären, warum dies geschieht.



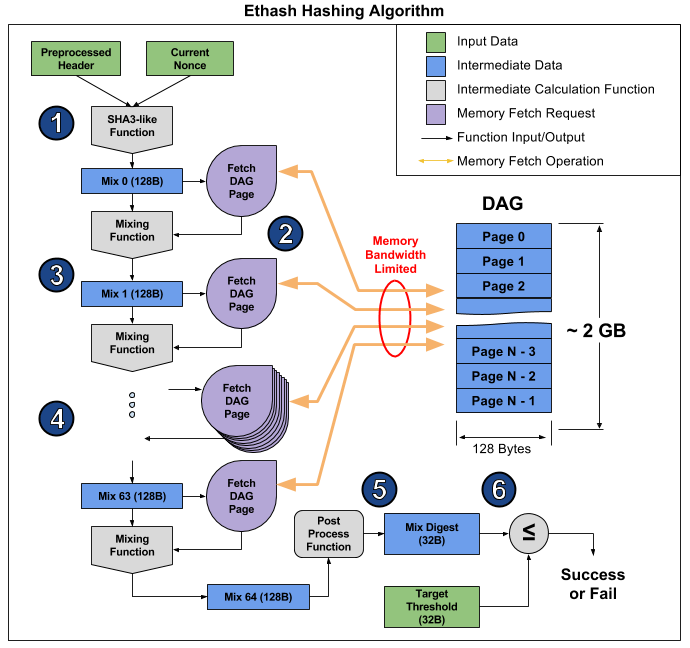
Der Artikel unterteilt den Algorithmus in 6 Punkte, aber 3 Stufen können für noch mehr Klarheit unterschieden werden:

1. Start: SHA-3 (512) zur Berechnung des ursprünglichen 128-Byte-Mix 0 (Punkt 1)
2. 64-fache Neuberechnung des Mix-Arrays durch Lesen der nächsten 128 Bytes und Mischen mit den vorherigen über die Mischfunktion für insgesamt 8 Kilobyte (Absätze 2-4)
3. Finalisierung und Überprüfung des Ergebnisses

Das Lesen von zufälligen 128 Bytes aus dem RAM dauert viel länger als es scheint. Wenn Sie die MSI RX 470-Grafikkarte mit 2048 Computergeräten und einer maximalen Speicherbandbreite von 211,2 GB / s verwenden, benötigen Sie für die Ausstattung jedes Geräts 1 / (211,2 GB / (128 b * 2048)) = 1241 ns oder etwa 1496 Zyklen mit einer bestimmten Frequenz. Angesichts der Größe der Mischfunktion können wir davon ausgehen, dass das Lesen des Speichers von einer Grafikkarte um ein Vielfaches länger dauert als das Neuberechnen der empfangenen Informationen. Infolgedessen nimmt Stufe 2 des Algorithmus viel Zeit in Anspruch, viel länger als die Stufen 1 und 3, die letztendlich nur geringe Auswirkungen auf die Leistung haben, obwohl sie mehr Berechnungen enthalten (hauptsächlich in SHA-3). Sie können sich nur die Hashrate dieser Grafikkarte ansehen: 26.375 Megaschritzen / s theoretisch (nur durch die Speicherbandbreite begrenzt) gegenüber 24 Megachehes / s tatsächlich, dh die Stufen 1 und 3 benötigen nur 10% der Zeit.

Auf S1 können alle 16 Multizellen parallel und mit unterschiedlichem Code arbeiten. Zusätzlich wird Zweikanal-RAM entlang eines Kanals für 8 Mehrzellen installiert. In Stufe 2 des Ethash-Algorithmus sieht unser Plan wie folgt aus: Eine Mehrfachzelle liest 128 Bytes aus dem Speicher und beginnt, sie neu zu zählen, dann liest die nächste den Speicher und zählt neu und so weiter bis zum 8., d. H. Eine Mehrfachzelle hat nach dem Lesen von 128 Byte Speicher 7 * [Lesezeit von 128 Byte], um das Array neu zu berechnen. Es wird angenommen, dass ein solcher Messwert 16 Zyklen dauert, d.h. 112 Maßnahmen werden zur Nachzählung angegeben. Die Berechnung der Mischfunktion dauert ungefähr den gleichen Taktzyklus, sodass S1 nahe am idealen Verhältnis von Speicherbandbreite zu Prozessorleistung liegt. Da in der zweiten Stufe keine Zeit verschwendet wird, sollten die verbleibenden Teile des Algorithmus so weit wie möglich optimiert werden, da sie sich dann wirklich auf die Leistung auswirken.

Um die Rechengeschwindigkeit SHA-3 (Keccak) zu bewerten, wurde ein C-Programm entwickelt und getestet, auf dessen Grundlage derzeit die optimale Version im Assembler erstellt wird. Die Auswertungsprogrammierung zeigt, dass eine Mehrzelle eine SHA-3 (Keccak) -Berechnung in 1550 Taktzyklen durchführt. Daher beträgt die Gesamtzeit für die Berechnung eines Hashs pro Multizelle 1550 + 64 * (16 + 112) = 9742 Zyklen. Bei einer Frequenz von 1,6 GHz und 16 parallelen Mehrfachzellen beträgt die Hash-Rate des Prozessors 2,6 MHash / s.

Beschleuniger	MultiClet S1	NVIDIA GeForce GTX 980 Ti	Radeon RX 470	Radeon RX Vega 64	NVIDIA GeForce GTX 1060	NVIDIA GeForce GTX 1080 Ti
Preis		$ 650	$ 180	500 Dollar	300 Dollar	$ 700
Hash-Rate	2,6 MHash / s	21,6 MHash / s	25,8 MHash / s	43,5 MHash / s	25 MHash / s	55 MHash / s
TDP	6 W.	250 W.	120 W.	295 W.	120 W.	250 W.
Hashrate / TDP	0,43	0,09	0,22	0,15	0,22	0,21
Prozesstechnik	28 nm	28 nm	14 nm	14 nm	16 nm	16 nm

Bei Verwendung von MultiClet S1 als Mining-Tool können tatsächlich 20 oder mehr Prozessoren auf den Platinen installiert werden. In diesem Fall ist die Hashrate einer solchen Karte gleich oder höher als die Hashraten vorhandener Grafikkarten, während der Stromverbrauch einer Karte mit S1 halb so hoch ist wie der von Grafikkarten mit topografischen Standards von 16 und 14 nm.

Abschließend muss ich sagen, dass die Hauptaufgabe jetzt die Herstellung einer Multiprozessor-Karte für einen mehrzelligen Cryptocurrency Miner und Supercomputing Miner ist. Die Wettbewerbsfähigkeit soll aufgrund des geringen Stromverbrauchs und der Architektur erreicht werden, die sich gut für beliebiges Computing eignen.

Der Prozessor befindet sich noch in der Entwicklung, aber Sie können bereits mit der Programmierung in Assemblersprache beginnen und die aktuelle Version des Compilers auswerten. Es gibt bereits ein minimales SDK mit Assembler, Linker, Compiler und Funktionsmodell, auf dem Sie Ihre Programme starten und testen können.