Hey, volle Stapel, lass uns die Fähigkeiten trainieren. Ich schlage vor, Gyrus zu kneten, es scheint mir interessant, dies mit einem anderen, ungewöhnlichen Paradigma zu tun. Die meisten Entwickler verfügen über eine ausgeprägte Fähigkeit zur Algorithmusisierung - die Aufgabe wird zu Bausteinen, die verbunden werden müssen, um über die Abfolge der Bewegungen nachzudenken, die zum gewünschten Ergebnis führen.
Hier wurde vor einer Woche der Prolog erwähnt, ich möchte antworten, dass die Prolog-Sprache zur Lösung von Problemen geeignet ist. Ich habe dieses Thema bereits angesprochen und mehrere Lösungen für zufällige Aufgaben zitiert, die mir von einer Site mit Aufgaben für Algorithmen zur Verfügung stehen. Ich möchte zeigen, dass jede komplexe Lösung in einer deklarativen Sprache verfügbar ist und nicht langsamer (naja, vielleicht merklich) funktionieren kann nicht sehr langsam).
Es hat lange gedauert, bis das nächste Problem vorgestellt wurde, und die erste Lösung ist bereits eingegangen. Ich demonstriere das Problem und finde heraus, wie langsam es ist.
Der Prolog ist insofern interessant, als Sie ein deduktives Programm erstellen können, das viele Lösungen zeigt und diese sogar einschränken kann, aber keine Möglichkeit zum Iterieren bietet.
Der Algorithmus wird entwickelt Löser Dolmetscher.
Die Aufgabe ist also :
- Regenwasser einfangen ii
Berechnen Sie anhand einer mxn-Matrix positiver Ganzzahlen, die die Höhe jeder Einheitszelle in einer 2D-Höhenkarte darstellt, das Wasservolumen, das sie nach dem Regen einfangen kann.
Hinweis:
Sowohl m als auch n sind kleiner als 110. Die Höhe jeder Einheitszelle ist größer als 0 und kleiner als 20.000.
Beispiel:
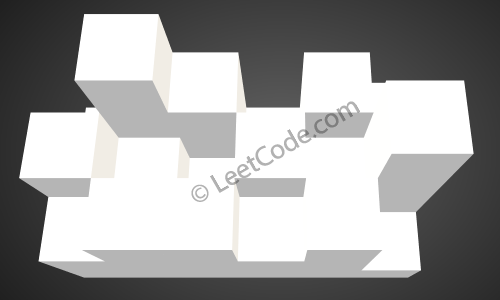
Gegeben die folgende 3x6 Höhenkarte:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]]
Rückgabe 4.
Nach langwierigen Versuchen, eine Lösung zu formulieren, kam ich zu folgendem Wortlaut:
Es ist notwendig, maximal Wasser in jede Zelle zu gießen, das nicht aus der Zelle austreten würde . Ich schlage vor, eine bestimmte Menge Wasser in jede Zelle zu gießen, aber damit es weniger als der maximal mögliche Wert ist.
Es stellte sich so heraus:
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!.
Dieses Prädikat nimmt die Eingabeliste (Matrix) und wandelt sie in eine Lösung um, in eine Matrix, in der es andere Werte gibt, die eine gültige Antwort sind. Dann nimmt ein anderes Prädikat diese beiden Listen Element für Element und ermittelt den Gesamtbetrag.
repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X).
Dieses Prädikat nimmt eine der Lösungen und prüft, ob es „normal“ gefüllt ist. Wenn es die Bedingung des Problems erfüllt, ist dies die Lösung.
Dies ist die Methode "generieren und überprüfen". Wir sagen, dass sich der Wert in einer solchen Menge befindet, und wir überarbeiten alle Elemente dieser Menge, indem wir eine Art von Exit-Bedingung überprüfen.
Dann erhalte ich eine neue Lösung mit dem Prädikat "Puts" (Vals, X0, X1). Hier ist zunächst eine Liste aller möglichen Höhen in dieser Matrix, aus der wir die möglichen Höhen für jede Zelle auswählen. Bei der Analyse der Eingangstests wurde festgestellt, dass es bei diesem Problem möglich ist, die gesamte Zelle zu füllen, wenn so viel Wasser um sie herum eingeführt werden kann, dass sie „über den Kopf“ gegossen wird.
Insgesamt sieht dieses Prädikat komplizierter aus. Es ist notwendig, die Dreifachlinien von Linien zu verarbeiten, die ein 3x3-Quadrat bilden (ja, es gibt kein Array im Prolog, aber es sieht aus wie die Beschreibung der Eingabedaten, und wir verwenden es in der deklarativen Programmierung. Möglicherweise kennen Sie die Indizes der Elemente im Array nicht gibt es nur eine Liste mit Kopf und Schwanz. Beschreiben Sie einfach eine Vorlage, die der Eingabespezifikation entspricht.
puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St).
Auf diese Weise wird ein Bypass der Matrix ausgedrückt, aus dem Sie die ersten drei (und weitere) Zeilen entnehmen können, aus denen Sie auch von links nach rechts drei Elemente auswählen können. Zwischen den acht Nachbarn befindet sich eine [Itaya] [Utaya] -Zelle der Landschaft. Mit Hilfe von sel_biger (R2, V, R21) wird eine neue Bedeutung dieser Zelle hergestellt.
Dieser Wert kann auf die aktuelle Zelle gesetzt werden, es kann eine der möglichen Höhen sein, und sogar die Liste wird in absteigender Reihenfolge sortiert, so dass die erste die höchste Höhe ist, die überhaupt verfügbar ist, und dann jede folgende:
sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X).
Es war eine Beschreibung eines „Entscheidungsgenerators“, und dann müssen Sie sicherstellen, dass die Matrix, die aus den willkürlich gefüllten Höhen an jedem Punkt erhalten wird, der von uns benötigten Antwort ähnlich ist.
Und es war erforderlich, einen solchen Zustand zu finden, dass sich das Wasser in den Löchern absetzt. Ich werde versuchen, es so auszudrücken:
von neun Werten eines Quadrats ist drei mal drei, in der Mitte sollte es immer eine solche Höhe geben, dass sie der Eingabekarte nicht widerspricht, so dass die ursprünglich in diesen Zellen vorgenommene Gleichgewichtsänderung nicht erhalten wurde, wenn es eine Höhe gab, dann sollten keine Zellen darüber sein, selbst wenn alles wird mit Wasser überflutet, dann können wir hier sagen, dass die hohe Zelle für sich bleiben oder durch einen höheren Wert ersetzt werden sollte, aber so, dass sie allen Nachbarn gleich ist, d. h. Die Zellen links, rechts und von oben nach unten vom Strom sollten größer oder gleich sein. Wenn sich mehr Wasser in der Zelle befindet, dann nur, wenn es um ... herum gestiegen ist.
Und die letzten beiden Prädikate, die die Eingabematrix verwenden, starten die Suche nach einem geeigneten Ergebnis, subtrahieren die Summe der Elemente untereinander und finden die endgültige Summe, die für das Problem erforderlich war:
diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. %% , sums(X,S):-reptest(X,X1),diffall(X,X1,S).
Ich werde die von der Website bereitgestellten Tests demonstrieren.
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). % balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). % , 33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). % , % equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-reptest(X,X1),diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([],0),true). :-assert_are_equal(sums([[1]],0),true). :-assert_are_equal(sums([[2,3]],0),true). :-assert_are_equal(sums([[3],[2]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). %:-assert_are_equal(sums([[9,9,9,9,9,9,8,9,9,9,9],[9,0,0,0,0,0,1,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,9,9,9,9,9,9,9,9,9,9]],215),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). %:-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true).
Ich musste die Tests kommentieren . nicht alle gingen durch.
Die Aufgabe ist, wie man es beschleunigt?
Einige Lösungen können aufgrund einer langen Suche nach Lösungen nicht gefunden werden. Sie werden in dieser Reihenfolge zu langsam generiert. Hier beträgt die Komplexität wahrscheinlich n! Alle möglichen Werte für jede Zelle des Arrays werden sortiert.
Es ist praktisch, diese Aufgabe in einem Programmiersystem in Einschränkungen auszudrücken. Nur im Prolog heißt sie wie folgt: CLP (FD): Constraint Logic Programming over Finite Domains.
clp (fd) ist eine Bibliothek, die in der Standard-SWI-Prolog-Distribution enthalten ist. Es löst Probleme mit Variablensätzen, bei denen die Beziehungen zwischen den Variablen erfüllt werden müssen.
>>
Ich formuliere das Problem folgendermaßen:
Wir brauchen eine solche Liste, bei der jedes Element des Wertesatzes in der gesamten Karte größer oder gleich seinem Maximalwert ist, wobei die Einschränkung berücksichtigt wird, dass die Elemente in der Reihenfolge der entsprechenden verschütteten Flüssigkeit klar angeordnet sein müssen.
So mache ich es aus der Eingabeliste, einer neuen Liste, deren Elemente in einem bestimmten Bereich unbekannt geworden sind (vom R2-Wert des aktuellen Elements bis zum Maximalwert von V).
Am Eingang eine Liste von Listen, am Ausgang eine neue Liste mit der maximalen Werteverteilung,
die die Begrenzung der "Flüssigkeitshaushalts" -Ballen erfüllen:
checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
Dies ist gleichzeitig ein Generator und eine Prüfung. Es wird angezeigt, dass sich die Elemente in einer solchen Menge befinden. Wenn dann nach und nach eine Prüfung durchgeführt wird, wird diese Menge eingegrenzt. Ferner bleibt etwas übrig und es kann "markiert" werden, d.h. Legen Sie ganzzahlige Werte fest, die die Summe aller Einschränkungen erfüllen. Das Aufrufen der Beschriftung ([unten], FX2) erzwingt das Füllen (Kontakt) Variablen Unbekannt mit bestimmten Werten, und es kann mehrere solcher Optionen geben, aber wir werden immer die allererste nehmen, da gesagt wurde, dass sich alle Variablen bei der Suche von ihren oberen Grenzen nach unten bewegen. Dies sind die Suchoptionen [nach unten].
Und dort sehen Sie so komplexe Einstellungen wie:16.2.1. Strategie zur Variablenauswahl
Mit der Variablenauswahlstrategie können Sie angeben, welche Variable von Vars als Nächstes gekennzeichnet ist und eine der folgenden ist:
ganz links - Beschriften Sie die Variablen in der Reihenfolge, in der sie in Vars vorkommen. Dies ist die Standardeinstellung.
ff Zuerst scheitern. Beschriften Sie die Variable ganz links mit der kleinsten Domäne als Nächstes, um die Unmöglichkeit frühzeitig zu erkennen. Dies ist häufig eine gute Strategie, wenn bei Auswahl einer ersten Variablen kleine Domänen für die nachfolgenden Variablen vorhanden sind.
ffc Von den Variablen mit den kleinsten Domänen wird die am weitesten links stehende Variable, die an den meisten Einschränkungen teilnimmt, als nächstes gekennzeichnet. Das Anwenden einer Einschränkung muss einen Teilbaum entfernen, daher kann dies eine gute Strategie sein.
min Beschriften Sie die Variable ganz links, deren untere Grenze die niedrigste nächste ist. Beachten Sie, dass dies min / 0 ist, anders als min / 1, was die Lösungslösung bestimmt und im vorherigen Abschnitt oben erläutert wurde. Dies ist eine gute Taktik, wenn Sie versuchen, einen globalen Wert zu minimieren, der wahrscheinlich niedriger ist, wenn verschiedene Variablen vorhanden sind (z. B. eine Lösung mit minimalen Kosten).
max Beschriften Sie die Variable ganz links, deren obere Grenze die höchste nächste ist. Auch dies unterscheidet sich von max / 1. Und der Rat für min gilt für max, wenn versucht wird, einen globalen Wert zu maximieren.
16.2.2. Wertreihenfolge
Die Wertreihenfolge ist eine von:
up Probieren Sie die Elemente der Domäne der ausgewählten Variablen in aufsteigender Reihenfolge aus. Dies ist die Standardeinstellung.
down Probieren Sie die Domain-Elemente in absteigender Reihenfolge aus.
Wenn Sie eine asymmetrische Verteilung haben, wie wir oben gezeigt haben, wie man effizient beschriftet, probieren Sie natürlich Elemente in der gängigsten ersten Reihenfolge aus.
16.2.3. Verzweigungsstrategie
Die Verzweigungsstrategie ist eine von:
Schritt Für jede Variable X wird eine Wahl zwischen X = V und X # \ = V getroffen, wobei V durch die Wertordnungsoptionen bestimmt wird. Dies ist die Standardeinstellung.
enum Für jede Variable X wird für alle Werte V_i der Domäne von X zwischen X = V_1, X = V_2 usw. gewählt. Die Reihenfolge wird durch die Wertordnungsoptionen bestimmt.
halbieren Für jede Variable X wird eine Wahl zwischen X # = <M und X #> M getroffen, wobei M der Mittelpunkt der Domäne von X ist. Wählen Sie diese Option, wenn viele Variablen eine Auswahl aus einem Bereich von ganzen Zahlen, einem Wert, sind. eher als einer unter einer Reihe von aufgezählten Werten (z. B. Prozentsätze, vs a = 0, b = 1, c = 2)
Was nun tatsächlich „ausgeglichen“ ist, ist, wenn das gegossene Wasser nicht von Zelle zu Zelle überläuft. Dies ist die Entsprechung der anfänglichen Reihenfolge der Elemente. Man könnte denken, dass das Füllen der Zellen die Form der ursprünglichen Landschaft beibehält, was bedeutet, dass wenn es eine Wand gab, diese mit Wasser bedeckt werden kann, so dass sie notwendigerweise allen Nachbarn gleich wird, oder wenn es keine Wand ist, die mit Wasser bedeckt ist ...
Betrachten Sie die ausgeglichenen Situationen:
-Wenn die Zelle überflutet ist, dann neben derselben oder sogar höher (plötzlich ist es die Wand).
-Wenn die Zelle gleich der Nachbarzelle war, sollte sie gleich der neuen Nachbarzelle sein.
- Und im Extremfall änderte die Zelle ihre Bedeutung nicht und dennoch, welche Art von Nachbarn sie hatte:
So können Sie Ihre Einstellung zur Aufgabe in das Programm übertragen. Es ist nicht notwendig, über einen Entscheidungsalgorithmus nachzudenken. Es ist wichtig, eine korrekte Beschreibung des Ergebnisses bereitzustellen, um alle anfänglichen Einschränkungen (Wertesätze) korrekt festzulegen. Dieser Ansatz kann einfach mit der üblichen Suche mit Rückkehr und Rekursion, die Prolog innewohnt, „gemischt“ werden. Auf diese Weise können Sie noch deklarativere Programme formulieren als mit den klassischen Prolog-Methoden.
Ich werde die erhaltene Lösung mit einer Reihe von Tests geben:
:- use_module(library(clpfd)). checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
Und noch mehr Tests :-assert_are_equal(sums([[13,16,15,18,15,15],[14,1,8,9,7,9],[19,5,4,2,5,10],[13,1,7,9,10,3],[17,7,5,10,6,1],[15,9,8,2,8,3]],36),true). :-assert_are_equal(sums([[18,13,13,17,12,11],[17,2,6,10,5,10],[11,10,2,8,8,2],[12,6,10,8,8,7],[18,4,7,6,7,4],[20,5,9,2,3,10]],18),true). :-assert_are_equal(sums([[14,20,11,19,19,16],[11,10,7,4,9,6],[17,2,2,6,10,9],[15,9,2,1,4,1],[15,5,5,5,8,7],[14,2,8,6,10,7]],11),true). :-assert_are_equal(sums([[19383,10886,12777,16915,17793,18335,15386,10492,16649,11421],[12362,27,8690,59,7763,3926,540,3426,9172,5736],[15211,5368,2567,6429,5782,1530,2862,5123,4067,3135],[13929,9802,4022,3058,3069,8167,1393,8456,5011,8042],[16229,7373,4421,4919,3784,8537,5198,4324,8315,4370],[16413,3526,6091,8980,9956,1873,6862,9170,6996,7281],[12305,925,7084,6327,336,6505,846,1729,1313,5857],[16124,3895,9582,545,8814,3367,5434,364,4043,3750],[11087,6808,7276,7178,5788,3584,5403,2651,2754,2399],[19932,5060,9676,3368,7739,12,6226,8586,8094,7539]],79058),true). :-assert_are_equal(sums([[10795,10570,11434,10378,17467,16601,10097,12902,13317,10492],[16652,756,7301,280,4286,9441,3865,9689,8444,6619],[18440,4729,8031,8117,8097,5771,4481,675,709,8927],[14567,7856,9497,2353,4586,6965,5306,4683,6219,8624],[11528,2871,5732,8829,9503,19,8270,3368,9708,6715],[16340,8149,7796,723,2618,2245,2846,3451,2921,3555],[12379,7488,7764,8228,9841,2350,5193,1500,7034,7764],[10124,4914,6987,5856,3743,6491,2227,8365,9859,1936],[11432,2551,6437,9228,3275,5407,1474,6121,8858,4395],[16029,1237,8235,3793,5818,4428,6143,1011,5928,9529]],68900),true). :-assert_are_equal(sums([[18776,12404,14443,15763,14613,14538,18606,16840,12904,14818],[15128,688,7369,7917,9917,6996,3324,7743,9470,2183],[18490,5499,9772,6725,5644,5590,7505,8139,2954,9786],[17669,8082,8542,8464,197,9507,9355,8804,6348,8611],[13622,7828,9299,7343,5746,5568,4340,5422,3311,3810],[17605,1801,5661,3730,4878,1305,9320,8736,9444,8626],[18522,3465,6708,3416,8282,3258,2924,7637,2062,5624],[12600,2036,3452,1899,9379,5550,7468,71,973,7131],[13881,4930,8933,5894,8660,163,7199,7981,8899,2996],[12959,3773,2813,9668,7190,1095,2926,6466,5084,1340]],61413),true). :-assert_are_equal(sums([[12090,17684,13376,15542,15936,19107,17445,19756,19179,18418],[16887,9412,3348,2172,1659,2009,2336,5210,6342,7587],[18206,9301,7713,7372,5321,1255,4819,4599,7721,9904],[15939,9811,3940,5667,1705,6228,1127,9150,5984,6658],[13920,9224,2422,7269,1396,4081,5630,84,9292,1972],[17672,3850,7625,5385,1222,9299,6640,6042,3898,713],[12298,6190,524,2590,8209,8581,8819,9336,7732,1155],[15994,8004,379,4769,5273,1776,8850,7255,1860,8142],[15579,5884,1993,3205,7621,9567,2504,613,1961,2754],[11326,4259,8944,8202,3202,3506,6784,2021,2842,868]],89383),true). :-assert_are_equal(sums([[19528,15189,18872,19908,19958,10498,18036,18808,17753,16248],[13303,3333,2133,1648,2890,9754,7567,1746,368,9529],[14500,8046,3788,9797,6249,6990,3303,3033,5363,2497],[10253,4892,7686,9125,1152,3996,5975,9188,9157,3729],[15436,2460,3414,3921,460,6304,28,8027,8050,6748],[17556,8902,4794,7697,8699,1043,1039,2002,428,6403],[14500,681,7647,8538,6159,5151,2535,2134,4339,1692],[12215,6127,504,5629,49,964,8285,6429,5343,6335],[13177,2900,5238,7971,6949,289,5367,7988,2292,5795],[10743,3144,2829,8390,1682,5340,3541,569,3826,4232]],100439),true).
Dies waren Tests von der Baustelle, nur die ersten 30 Stück. Das Ergebnis ist ausgezeichnet, das Problem ist gelöst und sogar schnell, immer bis zu einer Sekunde.
Sie können überprüfen ...
Als Fazit
Die deklarative Programmierung beinhaltet eine detaillierte Formalisierung der Aufgabe, und der Löser sucht nach der effektivsten Lösung, die die Bedingungen erfüllt.
Etwas tiefer in das Thema hinein können Sie minizinc öffnen, eine Programmiersprache, in die dieses Paradigma eingebettet ist. Sie formulierten viele Bedeutungen, wiesen auf Einschränkungen hin und voila, die Antwort. Sie lösen Sudoku , färben Karten, planen Arbeiten , Ressourcenprobleme und planen . Ich schlage vor zu trainieren ...