Mathe in Gamedev ist einfach. Triangulation und Triangle.Net in Unity

Hallo allerseits! Mein Name ist Grisha und ich bin der Gründer von CGDevs. Mathe ist ein sehr cooles Werkzeug bei der Entwicklung von Spielen. Wenn wir jedoch sagen, dass es schwierig ist, ohne das Verständnis von Vektoren und Matrizen auszukommen , sind Triangulationsalgorithmen nicht so notwendig, aber mit ihnen wird eine ziemlich große Anzahl interessanter Probleme gelöst. Heute möchte ich über ein ziemlich wichtiges Werkzeug in der Computergeometrie sprechen, wie Triangulationen und ihre Anwendung in der Spielebranche. Außerdem habe ich einen Port und einige Wrapper für die hervorragende Triangle.Net-Bibliothek für Unity geschrieben. Bei Interesse - willkommen bei cat. Link zum Github beigefügt.

Was ist Triangulation?

Im allgemeinen Fall ist die Triangulation eine Aufteilung eines geometrischen Objekts in Dreiecke. Dieses Konzept an sich ist recht einfach. Ein grundlegendes Beispiel für Triangulation bei Spiel-Engines ist ein Netz. Genau genommen kann ein Netz nicht nur aus Dreiecken bestehen, sondern in Spiel-Engines werden aus verschiedenen Gründen Netze aus Dreiecken genommen.



Triangulationen sind unterschiedlich, aber eine der beliebtesten Arten von Triangulationen ist die Delaunay-Triangulation. Diese Art der Triangulation zeichnet sich durch die Eigenschaft aus, dass in dem um jedes Dreieck umschriebenen Kreis nur die Eckpunkte dieses Dreiecks liegen.

Warum werden sie gebraucht?

Außerhalb der Spielebranche werden im Allgemeinen eine Vielzahl von Aufgaben mithilfe von Triangulationen gelöst. In Game Dev ist die erste Aufgabe, die mir in den Sinn kommt, das Navigationsnetz. Navmesh ist eine Datenstruktur, die bestimmt, wie viel Platz ein Spieler gehen kann. Es vermeidet so komplexe Rechenaufgaben wie das Bestimmen von Kollisionen mit einem Teil der Umgebung.

Das zweite interessante Problem, das mithilfe der Delaunay-Triangulation in der Spieleentwicklung gelöst werden kann, ist die Erzeugung von Terrains und Objekten, die als eine Reihe von Punkten dargestellt werden. Der Hauptvorteil der Delaunay-Triangulation in diesem Fall besteht darin, dass Sie aufgrund ihrer Eigenschaften sehr scharfe Dreiecke vermeiden können, die stören und Artefakte auf dem Tirrain erzeugen.



Darüber hinaus können Sie mithilfe der eingeschränkten Delaunay-Triangulation und Algorithmen wie dem zweiten Algorithmus von Chew und dem Algorithmus von Ruppert noch bessere Netze für Tirrains und gute Netze für eine andere Anwendung erzeugen - die Finite-Elemente-Methode.

Die Finite-Elemente-Methode selbst ist eine der Methoden, mit denen die Probleme der angewandten Physik gelöst werden. In Gamedev können Sie viele Probleme lösen, die mit der Simulation von Verformungen, Flüssigkeitssimulationen und anderen speziellen Problemen verbunden sind. Effekte. Normalerweise für die Aufzeichnung von Effekten in Animationen, da die Methode für Echtzeit einen zu hohen Rechenaufwand aufweist. Ein wichtiges Detail bei der Verwendung der Methode ist, dass der Fehler der Methode von den Winkeln der Dreiecke im Raster abhängt. Wenn das Gitter sehr scharfe Winkel enthält, gibt die Methode einen großen Fehler aus. Aus diesem Grund werden die oben aufgeführten Algorithmen benötigt.



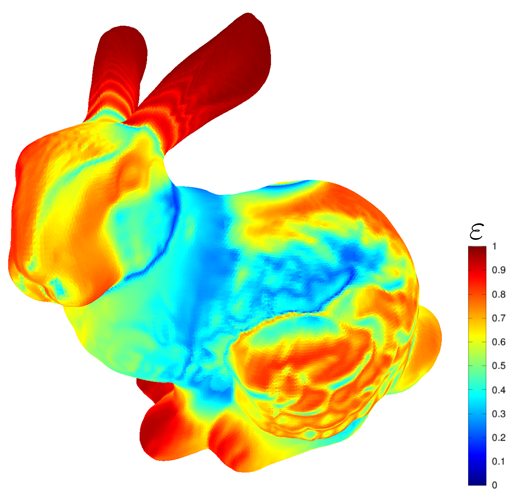
Und natürlich im Allgemeinen die prozedurale Netzgenerierung. Ein Github-Projekt zeigt beispielsweise eine Szene mit der Fähigkeit, Netze zu zeichnen. Einige physikalische Rätsel verwenden diese Anwendung als grundlegende Mechanik. Darüber hinaus ermöglichen Triangulationsalgorithmen die Verwendung der prozeduralen Generierung, um Probleme wie die prozedurale Zerstörbarkeit usw. zu lösen.

Zusätzlich zu Gamedev werden Triangulationen in Netzwerken, Computer Vision, verschiedenen analytischen Algorithmen sowie bei Problemen der Rechengeometrie verwendet, z. B. beim Kombinieren und Entfernen von Polygonen (was häufig bei Problemen bei der Entwicklung von Spielen hilfreich ist).

Ohrschneiden mit Löchern

Vielleicht einer der einfachsten Triangulationsalgorithmen. Es ergibt nicht das beste Gitter und hat im schlimmsten Fall die größte Rechenkomplexität O (n ^ 2).

Sie können mehr darüber in diesem Artikel lesen.

Bowyer-Watson-Algorithmus

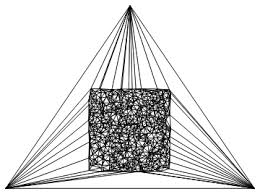
Ein Algorithmus, der eine Delaunay-Triangulation über eine Reihe von Punkten generiert. Wie bei den meisten Delaunay-Algorithmen beträgt die algorithmische Komplexität bei korrekter Implementierung im Allgemeinen O (n log n), wobei n die Anzahl der Eckpunkte ist. In einigen Fällen kann jedoch O (n ^ 2) erforderlich sein.

Die Nachteile beim Ohrschneiden bestehen darin, dass dieser Algorithmus eine konvexe Triangulation erstellt und in der Basisimplementierung keine Löcher im resultierenden Gitter enthält.

Delaunay-Verfeinerungsverarbeitung

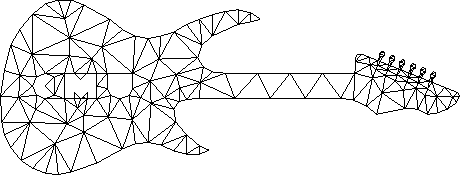
Der zweite Algorithmus von Chew und der Algorithmus von Ruppert sind Algorithmen, mit denen Sie Einschränkungen in die Delaunay-Triangulation eingeben und den Mindestwinkel des Dreiecks im Raster festlegen können. Ein wichtiges Detail der Algorithmen ist, dass sie in eine Endlosschleife gehen können und garantiert Ergebnisse bei Winkeln zwischen ungefähr 20,7 Grad und 29 Grad liefern. Die Fähigkeit, einen minimalen Winkel einzustellen, ist wichtig für die Lösung der oben beschriebenen Probleme.

Der zweite Algorithmus von Chew ist im kostenlosen Paket www.cs.cmu.edu/~quake/triangle.html und seinem Port auf .Net archive.codeplex.com/?p=triangle implementiert

Triangle.Net für die Einheit

Nun, da Sie mit Hilfe von Triangulationen so viele coole Aufgaben lösen können, wollte ich in den Ferien meinen Wrapper für Unity implementieren, damit ich immer ein handliches Werkzeug zur Hand habe. In dieser Implementierung arbeitet der Triangulationsalgorithmus im Durchschnitt für O (n) und im schlimmsten Fall für O (n * log n), wobei n die Anzahl der Eckpunkte ist. Beim Testen auf 1kk-Scheitelpunkte, die zufällig über ein Quadrat verteilt sind, haben die Einheiten im Editor des Intel Core i7-8700 beispielsweise in durchschnittlich 7,56 Sekunden ein Raster erstellt.

Die Hauptunterschiede zur ursprünglichen Bibliothek in Bezug auf auf Unity zugeschnittene Erweiterungsmethoden sowie das Ersetzen von double durch float in der gesamten Bibliothek (+ einige spezifische Operatoren für das Casting) Double in der Einheit sind wenig sinnvoll. Wenn wir physikalische Simulationen betrachten, würde ich eine separate Anwendung für eine Plus-Bibliothek verwenden, und das Ergebnis der Berechnungen gab Unity bereits nur zur Visualisierung. Außerdem wurde der Mesh-Typ in TriangleNetMesh umbenannt, um nicht relativ zum Mesh von Unity herunterzufahren. Ja, sie befinden sich bereits in einem anderen Namespace, aber ich denke, die Neuankömmlinge wären ein bisschen niedergeschlagen von der Tatsache, dass wir mit Hilfe eines Mesh ein anderes bekommen.

Das Wesentliche der Bibliothek ist, dass Sie zuerst das sogenannte Polygon angeben müssen. Generieren Sie dann darauf basierend bereits das Netz. Damit dies mit Einheitendatenstrukturen funktioniert, wurden verschiedene Erweiterungsmethoden eingeführt.



Zur Demonstration und Verwendung wurde eine spezielle Demoszene mit der Möglichkeit erstellt, Netze zu zeichnen. Sie können es und den Port der Bibliothek im Github-Projekt kennenlernen.

Vielen Dank für Ihre Aufmerksamkeit! Ich hoffe, dass der Port und der Artikel für jemanden nützlich sind und ein wenig klarer wird, warum Triangulation und Kenntnisse der Mathematik als Ganzes erforderlich sind. Ich werde weiterhin versuchen, Anwendungen und Methoden zur Lösung verschiedener mathematischer Probleme in der Spieleentwicklung offenzulegen. In der Computergeometrie selbst gibt es noch viele interessante Dinge, aber außerdem gibt es noch viele andere interessante Abschnitte der höheren Mathematik.