Betrachten Sie die Vorhersage von Zeitreihen. Lassen Sie uns versuchen, Anführungszeichen oder etwas anderes vorherzusagen, das sich als nützlich herausstellt.
Nehmen wir als Grundlage die Prognose, die im Artikel
Das Zeitreihen-Prognosemodell für das Beispiel der maximalen Ähnlichkeit vorgestellt wird: Erklärung und Beispiel (dieser Artikel gehört nicht mir). Der kurze Punkt ist, dass das ähnlichste Segment des Diagramms links von der Prognose in der Vergangenheit gesucht wird und von diesem alten Besten dann die Werte rechts vom Diagramm genommen und als Prognose verwendet werden.
Ich werde weiter gehen. Bei der Berechnung der Prognose nehme ich nicht einen Fall, der die beste Korrelation aufweist, sondern eine Packung der besten. Und die Prognose ist der Durchschnitt der Ergebnisse für dieses Paket. Dies macht es möglich zu verstehen, dass der gefundene Wert eine Regelmäßigkeit und kein zufälliges Zusammentreffen mit der gewünschten Prognose oder eine zufällige Abweichung ist, wenn die Prognose von der tatsächlichen abweicht.
Die Verwendung der besten Einzeloption wie in diesem Artikel ist nicht korrekt. Außerdem wird die Wahrscheinlichkeitsverteilung mit einem Wert aus dieser Verteilung bestimmt. Wenn Sie ein sehr großes Diagramm mit zufälligen Daten erstellen und eine Suche nach ihnen starten, werden sicherlich korrelierende Segmente darin sein, und möglicherweise sogar mit einem Koeffizienten von 0,9999, aber es ist überhaupt nicht notwendig, dass ähnliche Segmente diesen Segmenten weiterhin folgen - es ist immer noch so alles ist zufällig. Und Sie müssen nur eine Packung solcher Segmente nehmen und berechnen, dass die Varianz der nachfolgenden Daten geringer ist als die Varianz, die aus einer Zufallsstichprobe dieser Daten gebildet wird. Und wenn die Streuung der Packung geringer ist - dann ist dies die Prognose. Obwohl dies auch keine genaue Darstellung möglicher Fehler ist, reicht dies vorerst aus.
Das heißt,
Prognose ist nicht das Prinzip der Stichprobe und Korrelation der verglichenen Segmente, das wir verwenden. Hauptsache, dass aufgrund der Anwendung dieser Stichprobe die Varianz der gewünschten Werte geringer wäre als aufgrund der Zufallsstichprobe.
Die Varianz dieses Pakets ermöglicht es auch zu bewerten, welche Option besser aus früheren Fällen ausgewählt werden kann. Schließlich ist es möglich, nicht immer ein Segment korrelierender Daten auszuwählen und nicht immer die Pearson-Korrelation zu verwenden. Und eine solche Auswahl kann für jeden prognostizierten Punkt separat getroffen werden. Für welche Art von Stichprobe die Varianz geringer ist, ist diese Option für den aktuellen Punkt besser.
Welche Packungsgröße sollte es sein? Dies beruht auf der Frage der Konfidenzintervalle. Um nicht sehr viel zu laden, wird erwähnt, dass es besser ist, mindestens 30 Beispiele zu verwenden, um den Durchschnittswert zu bestimmen. Wenn es einen Überschuss an Testdaten gibt, würde ich mindestens 100 nehmen.
Das Verhältnis der Standardabweichungen der Stichprobe gemäß dem Algorithmus und dem zufälligen kann als theoretischer Erfolgskoeffizient des Prognosealgorithmus für den aktuellen Punkt zum Zwecke des Vergleichs mit anderen Stichprobenalgorithmen oder zur Bestimmung des Nutzens dieser Prognose im Allgemeinen bezeichnet werden, während der tatsächliche Wert noch nicht verfügbar ist.
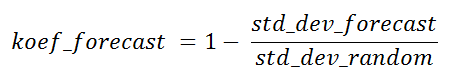
Dieser Koeffizient kann in einigen Fällen negative Werte annehmen. Die Punkte, an denen dies auftritt, sind von geringem Interesse, ebenso wie die Punkte mit einem Koeffizienten von Null. Bei einer Vorhersagbarkeit von 100% ist sie gleich eins.
Kommen wir noch einmal zu praktischen Beispielen aus diesem Artikel. Nachdem wir die kleinen Fehler dort korrigiert haben, erhalten wir das folgende Ergebnis, das mit diesem Artikel und diesem Algorithmus übereinstimmt:
Berechnung der Prognose zum Zeitpunkt 01.09.2012 23:00 Position 52631
Gesamtwerte auf Ähnlichkeit geprüft 2184
die beste Korrelation 0,958174 Position 52295
Übertragungskoeffizienten alpha (1/2) 1.03117 -11.1992
Prognosefehler von Fact Mape 5,210%mape - Der Begriff aus dem Originalartikel Mean Absolute Percentage Error wird nach der Formel berechnet
Abs (Prognose - Fakt) / FaktUnd jetzt treffen wir eine Auswahl nicht einer einzigen besten Ähnlichkeit, sondern einer Packung der besten und aller Dinge, um einen Moment vorherzusagen und zu sehen, was passiert:
0 korr 0,958174 pos 52295 mape 5,210%
1 korr 0,953571 pos 52151 mape 6,566%
2 korr 0,953532 pos 45599 mape 11,642%
3 korr 0,951462 pos 45743 mape 7,033%
4 korr 0,950921 pos 45575 mape 3,300%
5 korr 0,950789 pos 38687 mape 3,538%
Der Korrelationswert ändert sich hier von Wert zu Wert vernachlässigbar. Gleichzeitig variiert der Wert des Prognoseergebnisses zwischen 3% und 11%. Das heißt, Diese anfänglichen 5% sind nichts anderes als ein Zufall, sie könnten 11% und 3% sein.
Unter den in diesem Artikel angegebenen Ähnlichkeitsbedingungen können insgesamt 2184 Werte verglichen werden. Von diesen nahm ich eine Packung der Besten in 1500 Teilen, sortiert nach abnehmender Korrelation, und zeigte sie in einer Grafik an. Die Korrelation in dieser Packung von den besten 0,958 fiel von links nach rechts auf 0,715. Die Schwankung des Ergebnisses hat sich jedoch praktisch nicht geändert:

Es ist ersichtlich, dass die Abhängigkeit des Ergebnisses von der Korrelation sehr gering ist, aber es scheint trotzdem da zu sein. Im Allgemeinen nehmen wir eine Packung mit den Top-100-Werten und berechnen die Prognose, wie bereits erwähnt, anhand des Durchschnitts für diese Packung. Das Ergebnis ist wie folgt:
mape 5,824%, stddev mape 7,035% . Diese 5,8% sind jedoch kein Zufall mehr, sondern der Durchschnitt der Verteilung - die wahrscheinlichste Prognose. Die Mape-Standardabweichung ist größer als die Mape selbst, dies liegt jedoch daran, dass die Mape eine nicht symmetrische Verteilung aufweist.
Ich habe auch die gleiche Prognose berechnet, aber unter Verwendung einer bedingten Zufallsstichprobe, genauer gesagt, einfach gemittelt aus allen möglichen Optionen,
betrug das
Mape- Ergebnis
8,246% . Durch Zufallsstichprobe ist der Fehler etwas größer, aber dieser Wert liegt immer noch im Bereich der Streuung, die aus der besten Stichprobe berechnet wurde. Für den berechneten Punkt liegt der von mir angegebene theoretische Prognosekoeffizient nahe bei Null, genauer gesagt
koef_forecast = -0,041 . Ich habe es nicht aus stddev mape gezählt (es enthält die tatsächliche Prognose), sondern aus den absoluten Werten der Prognose. Wenn Sie sich das Programm ansehen, werden dort die Anfangszahlen dafür angegeben.
Dies gilt jedoch für den Zeitstempel, der im Originalartikel erwähnt wurde. Wenn wir jedoch "9/4/2012 23:00" (Monat / Tag / Jahr) sagen, dann ist der theoretische Effizienzkoeffizient
koef_forecast = 0,21 und
mape = 3,126%, mape_rand = 7,147% . Das heißt, koef_forecast hat im Voraus gezeigt, dass der aktuelle Punkt genauer berechnet wird als der vorherige. Das Wesentliche an der Nützlichkeit dieses Koeffizienten ist, dass Sie das Ergebnis zumindest irgendwie auswerten können, bevor Sie die tatsächlichen Daten erhalten, weil tatsächliche Daten nehmen nicht daran teil. Je höher es ist, desto besser. Ich habe bereits erwähnt, dass ein absolut vorhergesagter Punkt einen Koeffizienten von eins haben wird.
Sie können selbst sehen, wie sich all diese Zahlen in meinem Demo-Programm unter Qt C ++ ändern. Dort können Sie das Datum und die Größe des
Pakets auswählen: die
Quellen auf GithubDie besten Werte werden nach folgendem Algorithmus ausgewählt:
inline void OrdPack::add_value(double koef, int i_pos) { if (std::isfinite(koef)==false) return; if (koef <= 0.0) return; if (mmap_ord.size() < ma_count_for_pack) { if (mmap_ord.size()==0) mi_koef = koef; mi_koef = std::min(mi_koef, koef); mmap_ord.insert({-koef,i_pos}); } else if (koef > mi_koef) { mmap_ord.insert({-koef,i_pos}); while (mmap_ord.size() > ma_count_for_pack) mmap_ord.erase(--mmap_ord.end()); mi_koef = -(--mmap_ord.end())->first; } }
Es macht keinen Sinn, die gesamte Quelle hier zu veröffentlichen, es ist dort nicht kompliziert und mit Kommentaren. Die Basis in der Prozedur MainWindow :: to_do_test () in der Datei
mainwindow.cpp .
Im Moment werde ich weiterhin versuchen, im nächsten Teil etwas vorherzusagen.
PS. Bitte hinterlassen Sie Ihre Kommentare dazu, ob alles klar ist, was fehlt. Ich habe bereits einen ungefähren Plan für das, was als nächstes geschrieben werden soll, erstellt, aber mit Ihren Kommentaren werde ich es besser machen.