Theorie des Glücks. Statistik als wissenschaftlicher Weg, nichts zu wissen

Ich mache die Leser von Habr weiterhin mit den Kapiteln aus seinem Buch "Theory of Happiness" mit dem Untertitel "Mathematical Foundations of the Laws of Meanness" bekannt. Dieses populärwissenschaftliche Buch ist noch nicht veröffentlicht und erzählt sehr informell, wie Mathematik es Ihnen ermöglicht, die Welt und das Leben der Menschen mit einem neuen Grad an Bewusstsein zu betrachten. Es ist für diejenigen, die sich für Wissenschaft interessieren und für diejenigen, die sich für das Leben interessieren. Und da unser Leben komplex und im Großen und Ganzen unvorhersehbar ist, liegt der Schwerpunkt des Buches hauptsächlich auf der Wahrscheinlichkeitstheorie und der mathematischen Statistik. Hier werden Theoreme nicht bewiesen und die Grundlagen der Wissenschaft nicht gegeben, dies ist keineswegs ein Lehrbuch, sondern das, was man Freizeitwissenschaft nennt. Aber genau diese fast spielerische Herangehensweise ermöglicht es uns, Intuition zu entwickeln, Vorlesungen für Studenten mit anschaulichen Beispielen aufzuhellen und schließlich Nicht-Mathematikern und unseren Kindern zu erklären, was wir in unserer trockenen Wissenschaft so interessant fanden.


In diesem Kapitel geht es um Statistik, Wetter und sogar Philosophie. Mach dir keine Sorgen, nur ein bisschen. In einer anständigen Gesellschaft kann das nicht mehr für Tabletalk verwendet werden.

Die Zahlen täuschen, besonders wenn ich sie selbst mache; Bei dieser Gelegenheit ist die Aussage, die Disraeli zugeschrieben wird, wahr: "Es gibt drei Arten von Lügen: Lügen, offensichtliche Lügen und Statistiken."
Mark Twain

Wie oft planen wir im Sommer, ins Freie zu gehen, im Park spazieren zu gehen oder ein Picknick zu machen, und dann bricht der Regen unsere Pläne und sperrt uns im Haus ein! Und nun, wenn dies ein- oder zweimal in der Saison passiert ist, scheint es manchmal, dass das Wetter dem Wochenende folgt und immer wieder auf Samstag oder Sonntag kommt!

Ein relativ neuer Artikel wurde von australischen Forschern veröffentlicht: "Wöchentliche Zyklen der Spitzentemperatur und der Intensität der städtischen Wärmeinseln." Sie wurde von den Nachrichtenmedien aufgegriffen und druckte die Ergebnisse mit der folgenden Überschrift nach: „Glaubst du nicht! Wissenschaftler haben festgestellt, dass das Wetter am Wochenende wirklich schlechter ist als an Wochentagen. “ Das zitierte Papier liefert Statistiken über Temperatur und Niederschlag über viele Jahre in mehreren Städten in Australien und zeigt tatsächlich einen Temperaturabfall um bestimmte Stunden am Samstag und Sonntag. Danach wird eine Erklärung gegeben, die das lokale Wetter mit dem Grad der Luftverschmutzung aufgrund des zunehmenden Verkehrsflusses verbindet. Kurz zuvor wurde in Deutschland eine ähnliche Studie durchgeführt, die zu ungefähr den gleichen Ergebnissen führte.

Stimmen Sie zu, Bruchteile eines Grades sind ein sehr subtiler Effekt. Wir beschweren uns über das schlechte Wetter am lang erwarteten Samstag und diskutieren, ob der Tag sonnig oder regnerisch war. Diese Tatsache ist einfacher zu registrieren und später zu merken, ohne über genaue Instrumente zu verfügen. Wir werden unsere eigene kleine Studie zu diesem Thema durchführen und ein wunderbares Ergebnis erzielen: Wir können zuversichtlich sagen, dass wir nicht wissen, ob der Wochentag und das Wetter in Kamtschatka zusammenhängen. Studien mit einem negativen Ergebnis fallen normalerweise nicht auf die Seiten von Magazinen und in Newsfeeds, aber es ist wichtig, dass Sie und ich verstehen, auf welcher Grundlage ich im Allgemeinen sicher etwas über zufällige Prozesse sagen kann. Und in dieser Hinsicht ist ein negatives Ergebnis nicht schlechter als ein positives.

Ein Wort zur Verteidigung der Statistik

Statistiken werden für die Masse der Sünden verantwortlich gemacht: für Lügen und Manipulationsmöglichkeiten und schließlich für Unverständlichkeit. Aber ich möchte diesen Wissensbereich wirklich rehabilitieren, um zu zeigen, wie schwierig die Aufgabe ist, für die sie bestimmt ist, und wie schwierig es ist, die Antwort zu verstehen, die die Statistik gibt.

Die Wahrscheinlichkeitstheorie verwendet die genaue Kenntnis von Zufallsvariablen in Form von Verteilungen oder umfassenden kombinatorischen Berechnungen. Ich betone noch einmal, dass es möglich ist, eine Zufallsvariable genau zu kennen. Aber was ist, wenn dieses genaue Wissen für uns unzugänglich ist und wir nur über Beobachtung verfügen? Der Entwickler des neuen Arzneimittels hat eine begrenzte Anzahl von Tests, der Schöpfer des Verkehrsflusskontrollsystems hat nur eine Reihe von Messungen auf der realen Straße, der Soziologe hat die Ergebnisse von Umfragen, außerdem kann er sicher sein, dass die Befragten bei der Beantwortung einiger Fragen habe nur gelogen.

Es ist klar, dass eine Beobachtung überhaupt nichts gibt. Zwei - etwas mehr als nichts, drei, vier ... einhundert ... wie viele Beobachtungen benötigen Sie, um eine Zufallsvariable zu kennen, deren Sie sich mit mathematischer Präzision sicher sein können? Und was für ein Wissen wird es sein? Höchstwahrscheinlich wird es in Form einer Tabelle oder eines Histogramms dargestellt, das es ermöglicht, einige Parameter einer Zufallsvariablen auszuwerten. Sie werden als Statistik bezeichnet (z. B. Definitionsbereich, Mittelwert oder Varianz, Asymmetrie usw.). Wenn Sie sich das Histogramm ansehen, können Sie möglicherweise die genaue Form der Verteilung erraten. Aber Aufmerksamkeit! - Alle Beobachtungsergebnisse selbst sind Zufallsvariablen! Solange wir die Verteilung nicht genau kennen, geben uns alle Beobachtungsergebnisse nur eine probabilistische Beschreibung des Zufallsprozesses! Eine zufällige Beschreibung eines zufälligen Prozesses wäre hier immer noch nicht zu verwechseln oder möchte sogar absichtlich verwirren!

Was macht mathematische Statistik zu einer exakten Wissenschaft? Seine Methoden ermöglichen es uns, unsere Unwissenheit in einem klar begrenzten Rahmen zu schließen und ein berechenbares Maß an Vertrauen zu geben, dass unser Wissen innerhalb dieses Rahmens mit den Fakten übereinstimmt. Dies ist die Sprache, in der man über unbekannte Zufallsvariablen argumentieren kann, so dass das Denken Sinn macht. Ein solcher Ansatz ist sehr nützlich in der Philosophie, Psychologie oder Soziologie, wo es sehr einfach ist, lange zu argumentieren und zu diskutieren, ohne auf positives Wissen und insbesondere auf Beweise zu hoffen. Ein Großteil der Literatur widmet sich der kompetenten statistischen Datenverarbeitung, da sie ein absolut notwendiges Werkzeug für Ärzte, Soziologen, Ökonomen, Physiker, Psychologen ist ... kurz gesagt für alle Wissenschaftler, die die sogenannte "reale Welt" erforschen, die sich von der idealen Mathematik nur in dem Grad unserer Unkenntnis darüber unterscheidet.

Schauen Sie sich nun das Epigraph dieses Kapitels noch einmal an und stellen Sie fest, dass Statistiken, die so abfällig als dritter Grad der Lüge bezeichnet werden, die einzigen Dinge sind, die die Naturwissenschaften haben. Ist das nicht das Hauptgesetz der Gemeinheit des Universums? Alle uns bekannten Naturgesetze, von physikalisch bis wirtschaftlich, basieren auf mathematischen Modellen und ihren Eigenschaften, werden jedoch bei Messungen und Beobachtungen durch statistische Methoden verifiziert. Im Alltag macht unser Geist Verallgemeinerungen und beobachtet Muster, isoliert und erkennt sich wiederholende Bilder. Dies ist wahrscheinlich das Beste, was das menschliche Gehirn tun kann. Genau das lehrt künstliche Intelligenz heutzutage. Aber der Geist spart seine Kraft und neigt dazu, aus einzelnen Beobachtungen Schlussfolgerungen zu ziehen, ohne sich um die Richtigkeit oder Gültigkeit dieser Schlussfolgerungen zu sorgen. Bei dieser Gelegenheit gibt es eine wunderbare, in sich konsistente Aussage aus Stephen Brasts Buch Isola: „Jeder zieht allgemeine Schlussfolgerungen aus einem Beispiel. Zumindest mache ich genau das . “ Und während wir über Kunst, die Natur von Haustieren oder über Politik sprechen, können Sie sich darüber keine großen Sorgen machen. Wenn Sie jedoch ein Flugzeug bauen, einen Flughafen-Versanddienst organisieren oder ein neues Medikament testen, können Sie sich nicht mehr auf die Tatsache beziehen, dass „es mir scheint“, „die Intuition erzählt“ und „alles im Leben passiert“. Hier müssen Sie sich auf den Rahmen strenger mathematischer Methoden beschränken.

Unser Buch ist kein Lehrbuch, und wir werden statistische Methoden nicht im Detail untersuchen und uns nur auf eine Sache beschränken - die Technik des Testens von Hypothesen. Aber ich möchte den Verlauf der Argumentation und die Form der Ergebnisse zeigen, die für dieses Wissensgebiet charakteristisch sind. Und vielleicht werden einige der Leser, der zukünftige Student, nicht nur verstehen, warum sie ihn mit Statistiken, all diesen QQ-Diagrammen, t- und F-Verteilungen quälen, sondern es wird auch eine andere wichtige Frage auftauchen: Wie ist es möglich zu wissen, was - Sicherlich wegen eines Unfalls? Und was genau lernen wir mit Statistiken?

Drei Wale der Statistik

Die Hauptpfeiler der mathematischen Statistik sind die Wahrscheinlichkeitstheorie, das Gesetz der großen Zahlen und der zentrale Grenzwertsatz .

Das Gesetz der großen Zahlen legt in einer freien Interpretation nahe, dass eine große Anzahl von Beobachtungen einer Zufallsvariablen mit ziemlicher Sicherheit ihre Verteilung widerspiegelt , so dass die beobachteten Statistiken: Durchschnitt, Varianz und andere Merkmale dazu neigen, Werte zu exakt, die der Zufallsvariablen entsprechen. Mit anderen Worten, das Histogramm der beobachteten Werte mit einer unendlichen Anzahl von Daten tendiert mit ziemlicher Sicherheit zu der Verteilung, die wir als wahr betrachten können. Es ist dieses Gesetz, das die „alltägliche“ Frequenzinterpretation von Wahrscheinlichkeit und Theorie als Maß in einem Wahrscheinlichkeitsraum verbindet.

Der zentrale Grenzwertsatz besagt wiederum in einer freien Interpretation, dass eine der wahrscheinlichsten Formen der Verteilung einer Zufallsvariablen eine Normalverteilung (Gaußsche Verteilung) ist. Der genaue Wortlaut klingt anders: Der Durchschnittswert einer großen Anzahl identisch verteilter realer Zufallsvariablen, unabhängig von ihrer Verteilung, wird durch die Normalverteilung beschrieben. Dieser Satz wird normalerweise mit funktionalen Analysemethoden bewiesen, aber wir werden später sehen, dass er verstanden und sogar erweitert werden kann, indem das Konzept der Entropie als Maß für die Wahrscheinlichkeit eines Systemzustands eingeführt wird: Eine Normalverteilung hat die größte Entropie mit der geringsten Anzahl von Einschränkungen. In diesem Sinne ist es optimal, wenn eine unbekannte Zufallsvariable oder eine Zufallsvariable beschrieben wird, die eine Kombination vieler anderer Variablen ist, deren Verteilung ebenfalls unbekannt ist.

Diese beiden Gesetze liegen quantitativen Schätzungen der Zuverlässigkeit unseres Wissens zugrunde, die auf Beobachtungen beruhen. Hier geht es um die statistische Bestätigung oder Widerlegung der Annahme, die auf einigen gängigen Grundlagen und mathematischen Modellen beruhen kann. Dies mag seltsam erscheinen, aber Statistiken an sich bringen kein neues Wissen hervor. Eine Reihe von Fakten wird erst dann zu Wissen, wenn Verbindungen zwischen Fakten hergestellt werden, die eine bestimmte Struktur bilden. Es sind diese Strukturen und Beziehungen, die es uns ermöglichen, Vorhersagen zu treffen und allgemeine Annahmen zu treffen, die auf etwas basieren, das über die Statistik hinausgeht. Solche Annahmen nennt man Hypothesen . Es ist Zeit, sich an eines der Gesetze der Merphologie zu erinnern, das Persigue-Postulat :

Die Anzahl vernünftiger Hypothesen, die ein bestimmtes Phänomen erklären, ist unendlich.

Die Aufgabe der mathematischen Statistik besteht darin, diese unendliche Zahl zu begrenzen oder vielmehr auf eins zu reduzieren, und dies muss nicht unbedingt zutreffen. Um zu einer komplexeren (und oft wünschenswerteren) Hypothese überzugehen, ist es notwendig, anhand von Beobachtungsdaten die einfachere und allgemeinere Hypothese zu widerlegen oder sie zu verstärken und die Weiterentwicklung der Theorie aufzugeben. Die oft auf diese Weise getestete Hypothese wird als Null bezeichnet , und dies hat einen tiefen Sinn.

Was kann als Nullhypothese wirken? In gewissem Sinne alles, jede Aussage, aber unter der Bedingung, dass sie in die Sprache der Messung übersetzt werden kann. Am häufigsten ist die Hypothese der erwartete Wert eines Parameters, der sich während der Messung in eine Zufallsvariable verwandelt, oder das Fehlen einer Verbindung (Korrelation) zwischen zwei Zufallsvariablen. Manchmal wird angenommen, dass die Art der Verteilung, ein zufälliger Prozess, ein mathematisches Modell vorgeschlagen wird. Die klassische Formulierung der Frage lautet wie folgt: Erlauben uns Beobachtungen, die Nullhypothese abzulehnen oder nicht? Genauer gesagt, mit welcher Sicherheit können wir sagen, dass Beobachtungen nicht auf der Grundlage der Nullhypothese erhalten werden können? Wenn wir auf der Grundlage statistischer Daten nicht beweisen konnten, dass die Nullhypothese falsch ist, wird sie als wahr akzeptiert.

Und hier könnte man denken, dass Forscher gezwungen sind, einen der klassischen logischen Fehler zu machen, der den klangvollen lateinischen Namen ad ignorantiam trägt. Dies ist ein Argument für die Wahrheit einer Aussage, basierend auf dem Mangel an Beweisen für ihre Falschheit. Ein klassisches Beispiel sind die Worte von Senator Joseph McCarthy, als er gebeten wurde, Fakten vorzulegen, um seine Anschuldigung zu stützen, dass eine bestimmte Person Kommunist ist: „Ich habe nur wenige Informationen zu diesem Thema, außer der allgemeinen Aussage der zuständigen Behörden, dass sein Dossier nichts enthält seine Verbindungen zu den Kommunisten auszuschließen . " Oder noch heller: "Bigfoot existiert, da niemand etwas anderes bewiesen hat . " Das Erkennen des Unterschieds zwischen einer wissenschaftlichen Hypothese und ähnlichen Tricks ist Gegenstand eines ganzen Feldes der Philosophie: der Methodik wissenschaftlicher Erkenntnisse . Eines der bemerkenswerten Ergebnisse ist das Kriterium der Fälschbarkeit , das der bemerkenswerte Philosoph Karl Popper in der ersten Hälfte des 20. Jahrhunderts aufgestellt hat. Dieses Kriterium soll wissenschaftliche Erkenntnisse von unwissenschaftlichen trennen und erscheint auf den ersten Blick paradox:

Eine Theorie oder Hypothese kann nur dann als wissenschaftlich angesehen werden, wenn es auch hypothetisch einen Weg gibt, sie zu widerlegen.

Was ist nicht das Gesetz der Gemeinheit! Es stellt sich heraus, dass jede wissenschaftliche Theorie automatisch möglicherweise falsch ist und eine Theorie, die "per Definition" wahr ist, nicht als wissenschaftlich angesehen werden kann. Darüber hinaus erfüllen Wissenschaften wie Mathematik und Logik dieses Kriterium nicht. Sie beziehen sich jedoch nicht auf die Naturwissenschaften, sondern auf die formalen , für die kein Test auf Fälschbarkeit erforderlich ist. Und wenn wir noch ein Ergebnis derselben Zeit hinzufügen: Gödels Prinzip der Unvollständigkeit , das besagt, dass es innerhalb eines formalen Systems möglich ist, eine Aussage zu formulieren, die weder bewiesen noch widerlegt werden kann, dann kann unklar werden, warum man sich im Allgemeinen auf all diese Wissenschaft einlässt. Es ist jedoch wichtig zu verstehen, dass Poppers Fälschbarkeitsprinzip nichts über die Wahrheit einer Theorie aussagt, sondern nur, ob sie wissenschaftlich ist oder nicht. Es kann helfen festzustellen, ob eine Theorie eine Sprache gibt, in der es sinnvoll ist, über die Welt zu sprechen oder nicht.

Aber warum sind wir berechtigt, die Hypothese als wahr zu akzeptieren, wenn wir sie auf der Grundlage statistischer Daten nicht ablehnen können? Tatsache ist, dass die statistische Hypothese nicht dem Wunsch oder den Präferenzen des Forschers entnommen ist, sondern sich aus allgemeinen formalen Gesetzen ergeben sollte. Zum Beispiel aus dem zentralen Grenzwertsatz oder aus dem Prinzip der maximalen Entropie. Diese Gesetze spiegeln den Grad unserer Unwissenheit korrekt wider, ohne unnötig unnötige Annahmen oder Hypothesen hinzuzufügen. In gewissem Sinne ist dies eine direkte Verwendung des berühmten philosophischen Prinzips, das als Occams Rasiermesser bekannt ist :

Was auf der Grundlage weniger Annahmen getan werden kann, sollte nicht auf der Grundlage von mehr angenommen werden.

Wenn wir also die Nullhypothese akzeptieren, die auf dem Fehlen ihrer Widerlegung beruht, zeigen wir formal und ehrlich, dass der Grad unserer Unwissenheit als Ergebnis des Experiments auf dem gleichen Niveau geblieben ist . Im Beispiel des Bigfoot wird explizit oder implizit das Gegenteil angenommen: Das Fehlen von Beweisen dafür, dass diese mysteriöse Kreatur nicht etwas zu sein scheint, das den Grad unseres Wissens darüber erhöhen kann.

Im Allgemeinen ist unter dem Gesichtspunkt des Prinzips der Fälschbarkeit jede Aussage über die Existenz von etwas unwissenschaftlich, da der Mangel an Beweisen nichts beweist. Gleichzeitig kann die Behauptung des Fehlens von irgendetwas leicht widerlegt werden, indem eine Kopie, indirekte Beweise vorgelegt oder die Existenz einer Konstruktion nachgewiesen werden.In diesem Sinne analysiert ein statistischer Hypothesentest Vorwürfe über das Fehlen des gewünschten Effekts und kann in gewissem Sinne eine genaue Widerlegung dieser Aussage liefern. Genau das ist der Begriff „Nullhypothese“ völlig gerechtfertigt: Er enthält das notwendige Mindestwissen über das System.

Wie man Statistiken verwirrt und wie man sie entwirrt

Es ist sehr wichtig zu betonen, dass wenn die Statistiken zeigen, dass die Nullhypothese zurückgewiesen werden kann, dies nicht bedeutet, dass wir damit die Wahrheit einer alternativen Hypothese bewiesen haben. Statistiken sollten nicht mit Logik verwechselt werden, darin liegt eine Menge subtiler Fehler, insbesondere wenn bedingte Wahrscheinlichkeiten für abhängige Ereignisse ins Spiel kommen. Zum Beispiel: Es ist sehr unwahrscheinlich, dass eine Person der Papst sein kann ($$~ 1 / 7 Mrd.) folgt darausdass Papst Johannes Paul II kein Mann war? Die Aussage scheint absurd, aber leider ist eine solche „offensichtliche“ Schlussfolgerung genauso falsch: Der Test zeigte, dass ein mobiler Test auf Blutalkoholgehalt nicht mehr ergibt$\sim 1/7$$$1 % der falsch positiven und falsch negativen Ergebnisse, daher in$1\%$$$In 98 % der Fälle wird er einen betrunkenen Fahrer korrekt identifizieren. Lassen Sie uns testen$98\%$$$1000 Fahrer und lassen$1000$$$100 von ihnen werden wirklich betrunken sein. Als Ergebnis bekommen wir$100$$$900 × 1 % = 9 falsch positiv und$900\times1\%=9$$$100 × 1 % = 1 falsch negatives Ergebnis: Das heißt, für einen Betrunkenen, der hineingeschlichen ist, gibt es neun unschuldig beschuldigte zufällige Fahrer. Was ist nicht das Gesetz der Gemeinheit! Parität wird nur beobachtet, wenn der Anteil der betrunkenen Fahrer gleich ist$100\times1\%=1$$$$1/2$ , . , , !

. , : . , , . : .
Die Schnittwahrscheinlichkeit der Ereignisse A und B ist definiert als das Produkt aus der Wahrscheinlichkeit des Ereignisses B und der Wahrscheinlichkeit des Ereignisses $$A , wenn bekannt ist, dass ein Ereignis aufgetreten ist$A$$$$B$ ::

$$

$$P(A \cap B) = P(B)P(A|B).$$

Jetzt können Sie die Unabhängigkeit von Ereignissen auf drei äquivalente Arten bestimmen: Ereignisse $$$A$ und $$B unabhängig wenn$B$$$P ( A | B ) = P ( A ) oder$P(A|B) = P(A)$$$P ( B | A ) = P ( B ) oder$P(B|A) = P(B)$$$$P(A\cap B) = P(A)P(B)$ .
Damit ist die im ersten Kapitel begonnene formale Definition der Wahrscheinlichkeit abgeschlossen.

Schnittpunkt ist eine kommutative Operation, d.h.$$$P(A\cap B) = P(B\cap A)$ . Daraus folgt unmittelbar der Bayes-Satz

$$

$$P(A|B)P(B) = P(B|A)P(A),$$

die verwendet werden können, um bedingte Wahrscheinlichkeiten zu berechnen.

In unserem Beispiel mit Fahrern und einem Alkoholtest haben wir Ereignisse:$$A - der Fahrer ist betrunken,$A$$$B - Test ergab ein positives Ergebnis. Wahrscheinlichkeiten:$B$$$P ( A ) = 0,1 - die Wahrscheinlichkeit, dass der angehaltene Fahrer betrunken ist;$P(A) = 0.1$$$P ( B | A ) = 99 % - die Wahrscheinlichkeit, dass der Test ein positives Ergebnis liefert, wenn bekannt ist, dass der Fahrer betrunken ist (ausgeschlossen)$P(B|A) = 99\%$$$1 % falsch negativ)$1\%$$$P ( A | B ) = 99 % - die Wahrscheinlichkeit, dass der Test betrunken war, wenn der Test ein positives Ergebnis ergab (ausgeschlossen)$P(A|B) = 99\%$$$1 falsch positive Ergebnisse). Wir berechnen$1%$$$$P (B)$ - die Wahrscheinlichkeit, ein positives Testergebnis auf der Straße zu erzielen:

$$

$$P (B) = \ frac {P (A) P (A | B)} {P (B | A)} = P (A) = 0,1$$

Jetzt ist unsere Argumentation formalisiert und, wie Sie wissen, für manche Menschen vielleicht verständlicher. Das Konzept der bedingten Wahrscheinlichkeit ermöglicht es Ihnen, logisch in der Sprache der Wahrscheinlichkeitstheorie zu argumentieren. Es ist nicht überraschend, dass der Satz von Bayes eine breite Anwendung in der Entscheidungstheorie, in Mustererkennungssystemen, in Spamfiltern, in Programmen zum Testen von Plagiatstests und in vielen anderen Informationstechnologien gefunden hat.

Diese Beispiele werden von Studenten medizinischer Tests oder Rechtspraktiken sorgfältig verstanden. Ich befürchte jedoch, dass Journalisten oder Politikern weder mathematische Statistik noch Wahrscheinlichkeitstheorie beigebracht werden, aber sie appellieren eifrig an statistische Daten, interpretieren sie frei und bringen das gewonnene „Wissen“ in die Massen. Deshalb fordere ich meinen Leser auf: Ich habe die Mathematik selbst herausgefunden, hilf mir, sie für einen anderen herauszufinden! Ich sehe kein anderes Gegenmittel gegen Unwissenheit.

Wir messen unsere Leichtgläubigkeit

Wir werden nur eine der vielen statistischen Methoden betrachten und in der Praxis anwenden: das Testen statistischer Hypothesen. Für diejenigen, die ihr Leben bereits mit den Natur- oder Sozialwissenschaften verbunden haben, wird es in diesen Beispielen nichts erstaunlich Neues geben.

Angenommen, wir messen wiederholt eine Zufallsvariable mit einem Durchschnittswert $$$\ mu$ und Standardabweichung $$$\ sigma$ . Nach dem zentralen Grenzwertsatz wird der beobachtete Mittelwert normal verteilt. Aus dem Gesetz der großen Zahlen folgt, dass sein Durchschnitt dazu tendiert $$$\ mu$ und aus den Eigenschaften der Normalverteilung folgt, dass nach $$$n$ Messung wird die beobachtete Varianz des Mittelwerts als abnehmen $$$\ sigma / \ sqrt {n}$ . Die Standardabweichung kann als absoluter Fehler der Durchschnittsmessung betrachtet werden, der relative Fehler ist in diesem Fall gleich $$$\ delta = \ sigma / (\ sqrt {n} \ mu)$ . Dies sind sehr allgemeine Schlussfolgerungen, unabhängig von ausreichend großen $$$n$ aus der spezifischen Verteilungsform der untersuchten Zufallsvariablen. Daraus ergeben sich zwei nützliche Regeln (keine Gesetze):

1. Mindestanzahl von Tests $$$n$ sollte durch den gewünschten relativen Fehler diktiert werden $$$\ delta$ . Darüber hinaus, wenn

$$

$$n \ geq \ left (\ frac {2 \ sigma} {\ mu \ delta} \ right) ^ 2,$$

dann ist die Wahrscheinlichkeit, dass der beobachtete Durchschnitt innerhalb des angegebenen Fehlers bleibt, mindestens $$$95 \%$ . Bei $$$\ mu$ nahe Null ist der relative Fehler besser, um den absoluten zu ersetzen.

2. Die Hypothese sei die Nullhypothese, dass der beobachtete Mittelwert ist $$$\ mu$ . Dann, wenn der beobachtete Durchschnitt nicht darüber hinausgeht $$$\ mu \ pm 2 \ sigma / \ sqrt {n}$ dann ist die Wahrscheinlichkeit, dass die Nullhypothese wahr ist, mindestens $$$95 \%$ .


Wenn in diesen Regeln ersetzt $$$2 \ sigma$ auf $$$3 \ sigma$ dann steigt der Vertrauensgrad auf $$$99,7 \%$ Dies ist eine sehr starke Regel $$$3 \ sigma$ , was in den Naturwissenschaften Annahmen von experimentell festgestellten Tatsachen trennt.

Es wird für uns nützlich sein, die Anwendung dieser Regeln auf die Bernoulli-Verteilung zu betrachten, die eine Zufallsvariable beschreibt, die mit einer gegebenen Erfolgswahrscheinlichkeit genau zwei Werte annimmt, die bedingt als "Erfolg" und "Misserfolg" bezeichnet werden $$$p$ . In diesem Fall $$$\ mu = p$ und $$$\ sigma = \ sqrt {p (1-p)}$ Für die erforderliche Anzahl von Experimenten und das erforderliche Konfidenzintervall erhalten wir

$$

$$n \ geq \ frac {4} {\ delta ^ 2} \ frac {1-p} {p} \ quad und \ quad np \ pm 2 \ sqrt {np (1-p)}.$$

Die Regel $$$2 \ sigma$ Die Bernoulli-Verteilung kann verwendet werden, um das Konfidenzintervall beim Zeichnen von Histogrammen zu bestimmen. Im Wesentlichen repräsentiert jeder Balken des Histogramms eine Zufallsvariable mit zwei Werten: "Treffer" - "Fehlgeschlagen", wobei die Trefferwahrscheinlichkeit einer simulierten Wahrscheinlichkeitsfunktion entspricht. Zur Demonstration werden wir viele Stichproben für drei Verteilungen generieren: einheitlich, geometrisch und normal. Anschließend vergleichen wir die Schätzungen der Streuung der beobachteten Daten mit der beobachteten Streuung. Und hier sehen wir wieder die Echos des zentralen Grenzwertsatzes, der sich in der Tatsache manifestiert, dass die Verteilung der Daten um die Durchschnittswerte in den Histogrammen nahezu normal ist. Gegen Null wird die Streuung jedoch asymmetrisch und nähert sich einer anderen sehr wahrscheinlichen Verteilung - exponentiell. Dieses Beispiel zeigt gut, was ich damit gemeint habe, dass es sich in der Statistik um Zufallswerte von Parametern einer Zufallsvariablen handelt.


Beispiel, das das Verhältnis der durch die Regel vorgenommenen Streuschätzung zeigt $$$2 \ sigma$ und die beobachtete Streuung für drei Zufallsvariablen.

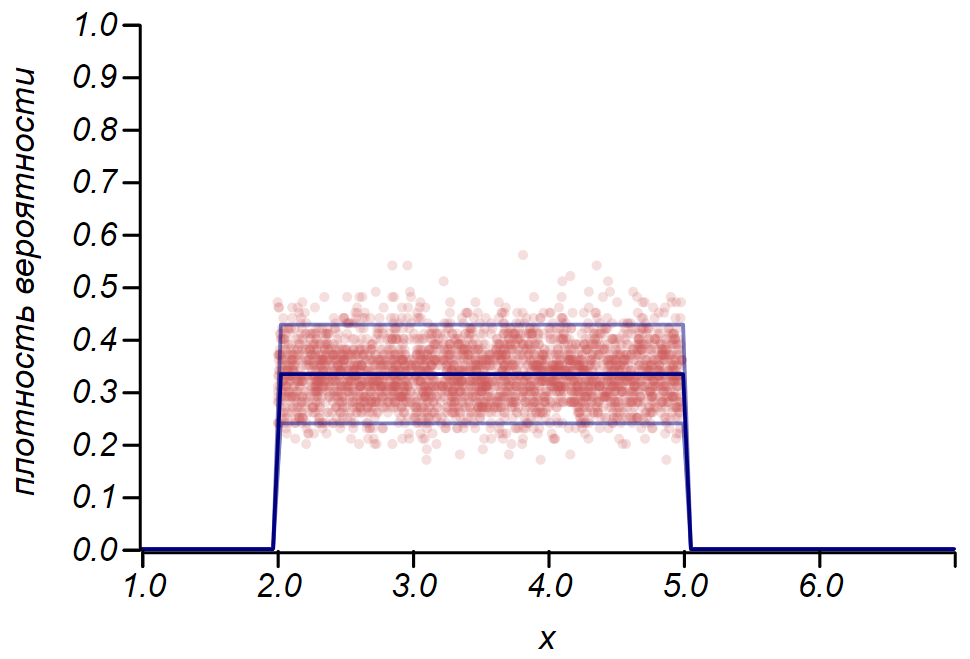
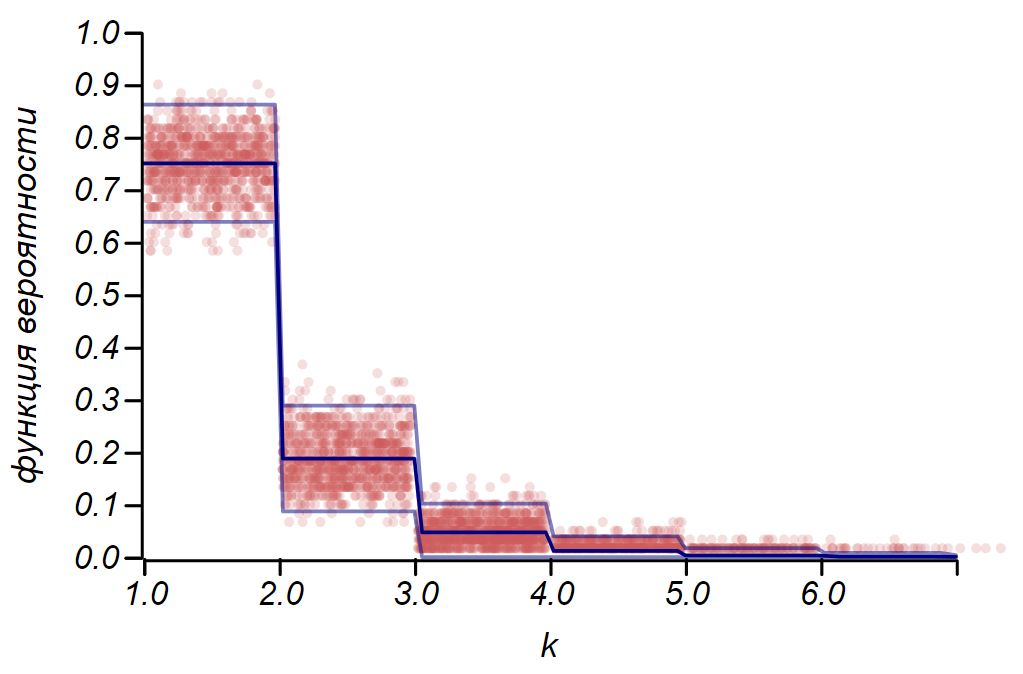
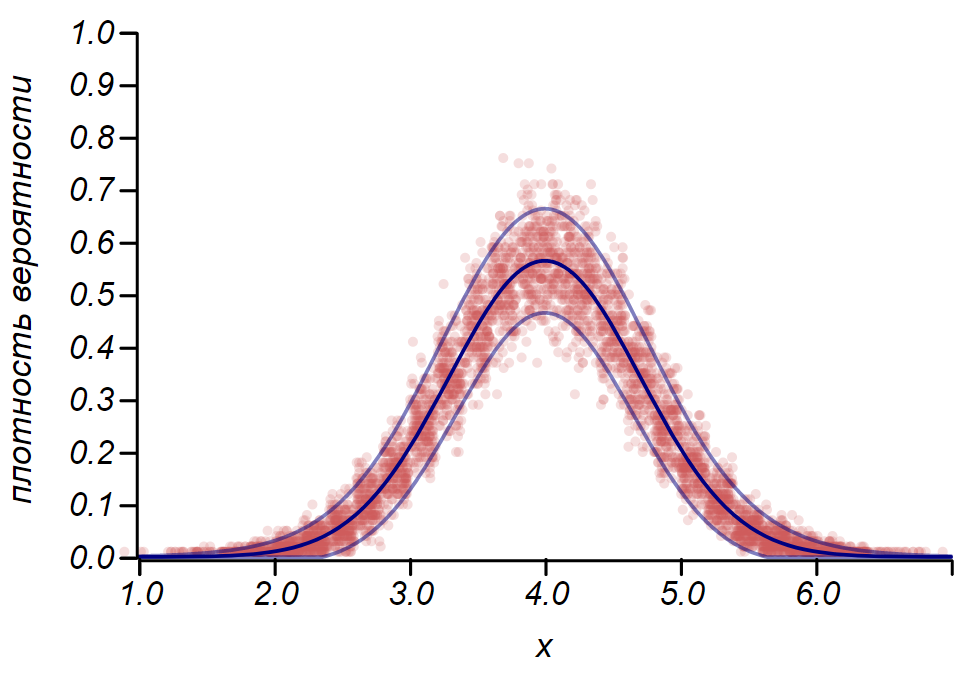
Es ist wichtig zu verstehen, dass die Regeln $$$2 \ sigma$ und sogar $$$3 \ sigma$ rette uns nicht vor Fehlern. Sie garantieren nicht die Wahrheit einer Aussage, sind keine Beweise. Statistiken begrenzen das Misstrauen gegenüber einer Hypothese und nichts weiter.

Der Mathematiker und Autor eines hervorragenden Kurses in Wahrscheinlichkeitstheorie, Gian Carlo Rota, gab in seinen Vorlesungen am MIT ein Beispiel. Stellen Sie sich eine wissenschaftliche Zeitschrift vor, deren Herausgeber eine willensstarke Entscheidung getroffen haben: ausschließlich Artikel mit positiven Ergebnissen zur Veröffentlichung anzunehmen, die der Regel entsprechen $$$2 \ sigma$ oder strenger. Gleichzeitig zeigt die redaktionelle Spalte an, dass die Leser das mit Wahrscheinlichkeit sicher sein können $$$95 \%$ Der Leser wird auf den Seiten dieses Magazins kein falsches Ergebnis finden! Leider kann diese Aussage leicht durch dieselbe Argumentation widerlegt werden, die uns zu eklatanter Ungerechtigkeit geführt hat, als wir Fahrer auf Alkohol getestet haben. Lass $$$1000$ Forscher erfahren $$$1000$ Hypothesen, von denen nur ein Teil wahr ist, sagen wir: $$$10 \%$ . Aufgrund der Bedeutung von Hypothesentests können wir dies erwarten $$$900 \ times0.05 = $ 4$ von falschen Hypothesen werden nicht fälschlicherweise zurückgewiesen und zusammen mit protokolliert $$$100 \ times0.95 = 95$ wahre Ergebnisse. Insgesamt von $$$130$ Ein gutes Drittel wird falsch sein!

Dieses Beispiel zeigt perfekt unser inneres Gesetz der Gemeinheit, das noch nicht in der Anthologie der Merphologie, dem Gesetz von Tschernomyrdin, enthalten ist :

Wir wollten das Beste, aber es stellte sich wie immer heraus.

Es ist einfach, eine allgemeine Schätzung des Prozentsatzes falscher Ergebnisse zu erhalten, die in den Ausgaben des Journals enthalten sein werden, vorausgesetzt, der Anteil der wahren Hypothesen ist $$$0 <\ alpha <1$ und die Wahrscheinlichkeit, eine fehlerhafte Hypothese zu akzeptieren, ist gleich $$$p$ ::

$$

$$x = \ frac {(1- \ alpha) p} {\ alpha (1-p) + (1- \ alpha) p}.$$

Die Bereiche, die den Anteil absichtlich falscher Ergebnisse begrenzen, die im Journal veröffentlicht werden können, sind in der Abbildung dargestellt.

Schätzung des Prozentsatzes der Veröffentlichungen, die offensichtlich falsche Ergebnisse enthalten, wenn verschiedene Kriterien zum Testen von Hypothesen übernommen werden. Es ist ersichtlich, dass Hypothesen durch die Regel akzeptiert werden $$$2 \ sigma$ kann während des Kriteriums riskant sein $$$4 \ sigma$ kann schon als sehr stark angesehen werden.

Das wissen wir natürlich nicht. $$$\ alpha$ und wir werden es nie erfahren, aber es ist sicherlich weniger als eine Einheit, was bedeutet, dass die Aussage aus der redaktionellen Kolumne auf jeden Fall nicht ernst genommen werden kann. Sie können sich auf starre Kriterien beschränken $$$4 \ sigma$ Es erfordert jedoch eine sehr große Anzahl von Tests. Daher ist es notwendig, den Anteil der wahren Hypothesen an den möglichen Annahmen zu erhöhen. Die Standardansätze der wissenschaftlichen Erkenntnismethode zielen darauf ab - die logische Konsistenz von Hypothesen, ihre Konsistenz mit Fakten und Theorien, die ihre Anwendbarkeit bewiesen haben, die Abhängigkeit von mathematischen Modellen und kritisches Denken.

Und wieder über das Wetter

Zu Beginn des Kapitels haben wir darüber gesprochen, dass Wochenenden und schlechtes Wetter häufiger zusammenfallen, als wir möchten. Versuchen wir, diese Studie abzuschließen. Jeder Regentag kann als Beobachtung einer Zufallsvariablen betrachtet werden - der Wochentag, der mit Wahrscheinlichkeit der Bernoulli-Verteilung folgt $$$1/7$ . Nehmen wir als Nullhypothese an, dass alle Wochentage in Bezug auf Wetter und Regen gleich sind und Regen in jedem von ihnen gleich wahrscheinlich regnen kann. Wir haben zwei freie Tage, so dass wir die erwartete Wahrscheinlichkeit eines Zusammentreffens eines schlechten Tages und eines gleichen freien Tages erhalten $$$2/7$ Dieser Wert ist der Bernoulli-Verteilungsparameter. Wie oft regnet es? Zu verschiedenen Jahreszeiten, natürlich auf unterschiedliche Weise, aber in Petropawlowsk-Kamtschatski gibt es durchschnittlich neunzig regnerische oder schneereiche Tage im Jahr. Der Strom von Tagen mit Niederschlag hat also eine Intensität von ungefähr $$$90/365 \ ca. 1/4$ . Berechnen wir, wie viele regnerische Wochenenden wir registrieren sollten, um sicherzugehen, dass es ein Muster gibt. Die Ergebnisse sind in der Tabelle aufgeführt.

Beobachtungszeitraum	Sommer	Jahr	$$$5$ Jahre
Erwartete Anzahl von Beobachtungen	$$$23$	$$$90$	$$$456$
Erwartete Anzahl positiver Ergebnisse	$$$6$	$$$26$	$$$130$
Signifikante Abweichung	$$$4$	$$$9$	$$$19$
Signifikanter Anteil der Schlechten Gesamtzahl der freien Tage	$$$42 \%$	$$$33 \%$	$$$29 \%$

Worüber sprechen diese Zahlen? Wenn es Ihnen so scheint, als ob es seit einem Jahr in Folge keinen Sommer mehr gibt, dieser böse Stein Ihr Wochenende verfolgt, indem er Regen an sie sendet, kann dies überprüft und bestätigt werden. Während des Sommers kann böser Stein jedoch nur gefangen werden, wenn mehr als zwei Fünftel aller Wochenenden regnerisch sind. Die Nullhypothese legt nahe, dass nur ein Viertel des Wochenendes mit schlechtem Wetter zusammenfallen sollte. In fünf Jahren Beobachtung kann man bereits hoffen, subtile Abweichungen zu bemerken, die darüber hinausgehen $$$5 \%$ und fahren Sie gegebenenfalls mit ihrer Erklärung fort.

Ich nutzte das Schulwettertagebuch, das von 2014 bis 2018 geführt wurde, und fand heraus, was in diesen fünf Jahren passiert ist $$$459$ Regentage von ihnen $$$141$ fiel am Wochenende. Dies ist in der Tat mehr als die erwartete Anzahl von $$$11$ Tage, aber signifikante Abweichungen beginnen mit $$$19$ Tage, also dies, wie wir in der Kindheit sagten: "zählt nicht." Hier finden Sie eine Reihe von Daten und ein Histogramm, das die Verteilung des schlechten Wetters nach Wochentagen zeigt. Die horizontalen Linien im Histogramm geben das Intervall an, in dem eine zufällige Abweichung von der Gleichverteilung für dieselbe Datenmenge beobachtet werden kann.


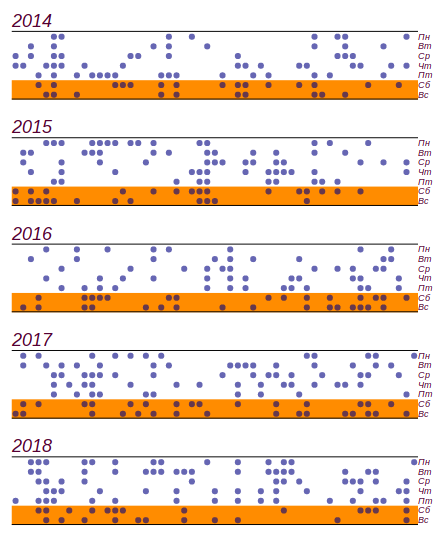
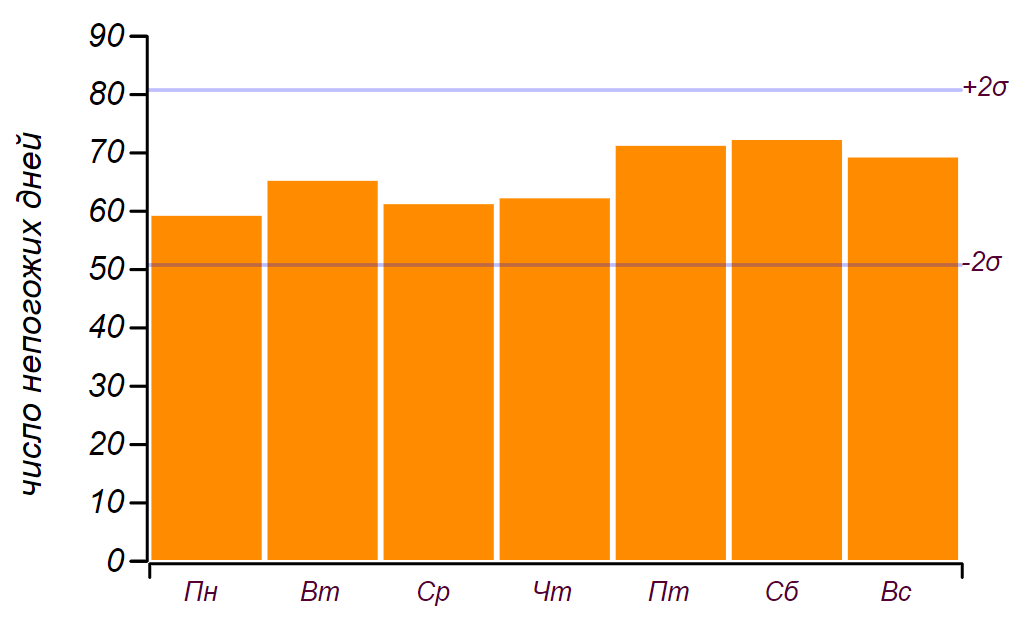Die ersten Datenreihen und die Verteilung der schlechten Tage nach Wochentagen wurden über einen Zeitraum von fünf Jahren beobachtet.

Es ist zu sehen, dass seit Freitag tatsächlich die Anzahl der Tage mit schlechtem Wetter zugenommen hat. Die Voraussetzungen reichen jedoch nicht aus, um einen Grund für dieses Wachstum zu finden: Das gleiche Ergebnis kann einfach durch Sortieren nach Zufallszahlen erzielt werden. Fazit: Während fünf Jahren Beobachtung des Wetters habe ich fast zweitausend Aufzeichnungen gesammelt, aber nichts Neues über die Verteilung des Wetters nach Wochentagen erfahren.

Wenn Sie sich die Tagebucheinträge ansehen, wird deutlich, dass das Wetter nicht alleine kommt, sondern in zwei- bis dreitägigen Perioden oder sogar wöchentlichen Zyklonen. Beeinflusst dies irgendwie das Ergebnis? Sie können versuchen, diese Beobachtung zu berücksichtigen und davon ausgehen, dass es durchschnittlich zwei Tage lang regnet (tatsächlich $$$1,7$ Tage), dann steigt die Wahrscheinlichkeit, das Wochenende zu blockieren, auf $$$3/7$ . Mit einer solchen Wahrscheinlichkeit sollte die erwartete Anzahl von Spielen für fünf Jahre sein $$$195 \ pm21$ d.h. von $$$174$ vorher $$$216$ mal. Beobachteter Wert $$$141$ fällt nicht in diesen Bereich und daher kann die Hypothese der Auswirkung von zwei Tagen schlechten Wetters sicher zurückgewiesen werden. Haben wir etwas Neues gelernt? Ja, wir haben gelernt: Es scheint, dass ein offensichtliches Merkmal des Prozesses keine Auswirkungen hat. Dies ist eine Überlegung wert, und wir werden es etwas später tun. Die Hauptschlussfolgerung ist jedoch, dass es keine Gründe gibt, subtilere Auswirkungen in Betracht zu ziehen, da die Beobachtungen und vor allem ihre Anzahl konsequent für die einfachste Erklärung sprechen.

Aber unser Missfallen ist keine Fünfjahres- oder sogar Jahresstatistik, das menschliche Gedächtnis ist nicht so lang. Es ist eine Schande, wenn es am Wochenende drei- oder viermal hintereinander regnet! Wie oft kann dies beobachtet werden? Besonders wenn Sie sich daran erinnern, dass das böse Wetter nicht alleine kommt. Die Aufgabe kann wie folgt formuliert werden: „Wie hoch ist die Wahrscheinlichkeit, dass $$$n$ Wochenende in Folge wird es regnen? " Es ist anzunehmen, dass schlechtes Wetter einen Poisson-Strom mit Intensität bildet $$$1/4$ . Dies bedeutet, dass im Durchschnitt ein Viertel der Tage eines Zeitraums schlecht ist. Wenn wir nur das Wochenende beobachten, sollten wir die Intensität des Flusses nicht ändern, und von allen Wochenenden sollte das schlechte Wetter im Durchschnitt auch ein Viertel betragen. Wir stellen also die Nullhypothese auf: Der Sturm ist Poisson mit einem bekannten Parameter, was bedeutet, dass die Intervalle zwischen Poisson-Ereignissen durch eine Exponentialverteilung beschrieben werden. Wir interessieren uns für diskrete Intervalle: $$$0, \ 1, \ 2, \ 3$ Tage usw. können wir daher das diskrete Analogon der Exponentialverteilung verwenden - die geometrische Verteilung mit dem Parameter $$$1/4$ . Die Abbildung zeigt, was wir getan haben, und es ist ersichtlich, dass die Annahme, dass wir den Poisson-Prozess beobachten, nicht vernünftig ist, abzulehnen.


Die beobachtete Verteilung der Länge der Ketten von fehlgeschlagenen Wochenenden und theoretischen. Die dünne Linie zeigt die zulässigen Abweichungen für die Anzahl der Beobachtungen, die wir haben.

Sie können sich folgende Frage stellen: Wie viele Jahre brauchen Sie, um Beobachtungen zu machen, damit der Unterschied in $$$11$ Tage könnten sicher bestätigt oder als zufällige Abweichung abgelehnt werden? Es ist einfach zu berechnen: beobachtete Wahrscheinlichkeit $$$141/459 = 0,307$ anders als erwartet $$$2/7 = $ 0,28$ auf $$$0,02$ . Um Unterschiede in Hundertsteln aufzuzeichnen, ein absoluter Fehler von nicht mehr als $$$0,005$ das macht $$$1,75 \%$ von der gemessenen Größe. Von hier erhalten wir die erforderliche Stichprobengröße $$$n \ geq (4 \ cdot 5/7) / (0,0175 ^ 2 \ cdot 2/7) \ ca. 32000$ Regentage. Es wird ungefähr dauern $$$4 \ cdot 32000/365 \ ca. 360$ Jahre kontinuierlicher meteorologischer Beobachtungen, weil es nur jeden vierten Tag regnet oder schneit. Leider ist dies mehr als die Zeit, in der Kamtschatka Teil Russlands ist, daher habe ich keine Chance herauszufinden, wie die Dinge "wirklich" sind. Vor allem, wenn man bedenkt, dass sich das Klima in dieser Zeit dramatisch verändert hat - seit der kleinen Eiszeit kam die Natur zum nächsten Optimum heraus.

Wie haben australische Forscher es geschafft, die Temperaturabweichung in Bruchteilen eines Grades zu erfassen, und warum ist es sinnvoll, diese Studie in Betracht zu ziehen? Tatsache ist, dass sie stündliche Temperaturdaten verwendeten, die durch keinen zufälligen Prozess „ausgedünnt“ wurden. Also darüber hinaus $$$30$ Durch jahrelange meteorologische Beobachtungen konnten mehr als eine Viertelmillion Messwerte gesammelt werden, was die Standardabweichung verringert $$$500$ Zeiten in Bezug auf die tägliche Standardtemperaturabweichung. Dies reicht aus, um über Genauigkeit in Zehntelgraden zu sprechen. Darüber hinaus verwendeten die Autoren eine andere schöne Methode, die das Vorhandensein eines Zeitzyklus bestätigt: das zufällige Mischen der Zeitreihen. Ein solches Mischen bewahrt statistische Eigenschaften wie die Fließintensität, löscht jedoch die zeitlichen Muster und macht den Prozess zu einem echten Poisson. Durch den Vergleich vieler synthetischer und experimenteller Reihen können wir überprüfen, ob die beobachteten Abweichungen des Prozesses von Poisson signifikant sind. In gleicher Weise zeigte der Seismologe A. A. Gusev , dass Erdbeben in jeder Region eine Art selbstähnlichen Fluss mit den Eigenschaften der Clusterbildung bilden. Dies bedeutet, dass Erdbeben dazu neigen, sich mit der Zeit zu sammeln und sehr unangenehme Strömungsdichtungen zu bilden. Später stellte sich heraus, dass die Folge großer Vulkanausbrüche die gleiche Eigenschaft hat.

Eine weitere Quelle der Zufälligkeit

Natürlich kann das Wetter wie Erdbeben nicht durch den Poisson-Prozess beschrieben werden - dies sind dynamische Prozesse, bei denen der aktuelle Zustand eine Funktion der vorherigen ist. Warum bevorzugen unsere wöchentlichen Wetterbeobachtungen ein einfaches stochastisches Modell? Tatsache ist, dass wir den regulären Prozess der Niederschlagsbildung für einen Satz von sieben Tagen oder, in der Sprache der Mathematik, auf einem System von Abzügen Modulo 7 anzeigen. Dieser Projektionsprozess kann aus geordneten Datenreihen Chaos erzeugen. Ab hier gibt es zum Beispiel eine sichtbare Zufälligkeit in der Ziffernfolge der Dezimalschreibweise der meisten reellen Zahlen.

Wir haben bereits über rationale Zahlen gesprochen, die als ganzzahlige Brüche ausgedrückt werden. Sie haben eine interne Struktur, die durch zwei Zahlen bestimmt wird: den Zähler und den Nenner. Wenn Sie jedoch in Dezimalform schreiben, können Sie bei der Darstellung von Zahlen wie z $$$1/2 = 0,5 \ overline {0}$ oder $$$1/3 = 0. \ Overline {3}$ zur periodischen Wiederholung bereits recht zufälliger Folgen in Zahlen wie $$$1/17 = 0. \ Overline {0588235294117647}$ . Irrationale Zahlen haben keine endliche oder periodische Dezimalschreibweise, und in diesem Fall herrscht das Chaos am häufigsten in einer Folge von Zahlen. Dies bedeutet jedoch nicht, dass diese Zahlen keine Reihenfolge aufweisen! Zum Beispiel die erste irrationale Zahl, auf die Mathematiker stoßen $$$\ sqrt {2}$ in Dezimalschreibweise wird eine zufällige Menge von Zahlen erzeugt. Andererseits kann diese Zahl jedoch als unendlicher fortgesetzter Bruch dargestellt werden:

$$

$$\ sqrt {2} = 1 + \ frac {1} {2+ \ frac {1} {2+ \ frac {1} {2+ ...}}}.$$

Es ist leicht zu zeigen, dass diese Kette tatsächlich gleich der Wurzel von zwei ist, indem man die Gleichung löst:

$$

$$x-1 = \ frac {1} {2+ (x-1)}.$$

Fortgesetzte Brüche mit sich wiederholenden Koeffizienten werden kurz geschrieben, wie periodische Dezimalbrüche, zum Beispiel: $$$\ sqrt {2} = [1, \ bar {2}]$ , $$$\ sqrt {3} = [1, \ overline {1,2}]$ . Der berühmte goldene Schnitt in diesem Sinne ist die am einfachsten angeordnete irrationale Zahl: $$$\ varphi = [1, \ bar {1}]$ . Alle rationalen Zahlen werden in Form von endlichen fortgesetzten Brüchen dargestellt, einige irrational - in Form von unendlichen, aber periodischen, sie werden algebraisch genannt , dieselben, die selbst in dieser Form keine endliche Notation haben - transzendent . Das berühmteste der Transzendentalen ist die Zahl $$$\ pi$ , es schafft Chaos sowohl in Dezimalzahl als auch in Form eines fortgesetzten Bruches: $$$\ pi \ ca. [3, 7,15,1,292,1,1,1,2,1,3,1,14,2,1, ...]$ . Und hier ist die Eulernummer $$$e$ Das verbleibende Transzendentale in Form eines fortgesetzten Bruches zeigt die interne Struktur an, die in der Dezimalschreibweise verborgen ist: $$$e \ ca. [2,1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...]$ .

Wahrscheinlich ahnte kein einziger Mathematiker, der mit Pythagoras begann, die Welt der List und entdeckte, was benötigt wird, eine so grundlegende Zahl $$ p i hat eine so schwer fassbare chaotische Struktur. Natürlich kann es als Summe ziemlich eleganter numerischer Reihen dargestellt werden, aber diese Reihen sprechen nicht direkt über die Natur dieser Zahl und sind nicht universell. Ich glaube, dass die Mathematiker der Zukunft eine neue Darstellung von Zahlen entdecken werden, so universell wie fortgesetzte Brüche, die die strenge Ordnung offenbaren wird, die die Natur in Zahlen verbirgt.$\ pi$

$$

$$*\ *\ *$$

Die Ergebnisse dieses Kapitels sind größtenteils negativ. Und als Autor, der den Leser mit versteckten Mustern und unerwarteten Entdeckungen überraschen möchte, bezweifelte ich, dass es in das Buch aufgenommen werden sollte. Unser Gespräch über das Wetter ging jedoch auf ein sehr wichtiges Thema ein - den Wert und die Aussagekraft des naturwissenschaftlichen Ansatzes.

Ein weises Mädchen, Sonya Shatalova, die im Alter von zehn Jahren die Welt durch das Prisma des Autismus betrachtete, gab eine sehr präzise und präzise Definition: „Wissenschaft ist ein Wissenssystem, das auf Zweifeln beruht.“. Die reale Welt ist instabil und bemüht sich, sich hinter der Komplexität, sichtbaren Zufälligkeit und Unzuverlässigkeit von Messungen zu verstecken. Zweifel in den Naturwissenschaften sind unvermeidlich. Die Mathematik scheint ein Bereich der Gewissheit zu sein, in dem man anscheinend Zweifel vergessen kann. Und es ist sehr verlockend, sich hinter den Mauern dieses Königreichs zu verstecken; Betrachten Sie anstelle der nicht erkennbaren Weltmodelle, die gründlich untersucht werden können. zählen und berechnen, der Nutzen der Formel ist bereit, alles zu verdauen. Dennoch ist Mathematik eine Wissenschaft, und Zweifel daran sind eine tiefe innere Ehrlichkeit, die keine Ruhe gibt, bis die mathematische Konstruktion von zusätzlichen Annahmen und unnötigen Hypothesen befreit ist. Im Bereich der Mathematik sprechen sie eine komplexe, aber harmonische Sprache, die sich zum Nachdenken über die reale Welt eignet. Es ist sehr wichtig, sich mit dieser Sprache vertraut zu machen.um zu verhindern, dass die Zahlen vorgeben, Statistiken zu sein, dass Fakten nicht vorgeben, Wissen zu sein, und dass Unwissenheit und Manipulation der realen Wissenschaft gegenüberstehen.