Hallo allerseits! Mein Name ist Grisha und ich bin der Gründer von CGDevs. Reden wir weiter über Mathe oder so. Vielleicht ist VFX die Hauptanwendung der Mathematik in der Spieleentwicklung und der Computergrafik im Allgemeinen. Sprechen wir also über einen solchen Effekt - Regen oder vielmehr über seinen Hauptteil, der Mathematik erfordert - Wellen auf der Oberfläche. Schreiben Sie nacheinander einen Shader für Wellen auf der Oberfläche und analysieren Sie dessen Mathematik. Bei Interesse - willkommen bei cat. Github-Projekt beigefügt.
Manchmal kommt ein Moment im Leben, in dem ein Programmierer sich ein Tamburin schnappen und nach Regen rufen muss. Im Allgemeinen ist das Thema der Regenmodellierung selbst sehr tiefgreifend. Es gibt viele mathematische Arbeiten zu verschiedenen Teilen dieses Prozesses, von Tropfen und den damit verbundenen Effekten bis zur Verteilung der Tröpfchen im Volumen. Wir werden nur einen Aspekt analysieren - den Shader, mit dem wir aus einem Tropfen einen Effekt erzeugen können, der der Welle ähnelt. Es ist Zeit, ein Tamburin zu nehmen!
Mathe WelleWenn Sie im Internet suchen, finden Sie viele lustige mathematische Ausdrücke zum Erzeugen von Wellen. Oft bestehen sie aus einer Art "magischen" Zahlen und periodischen Funktionen ohne Begründung. Im Allgemeinen ist die Mathematik dieses Effekts jedoch recht einfach.
Wir brauchen im eindimensionalen Fall nur eine ebene Wellengleichung. Warum wir etwas später flach und eindimensional analysieren werden.
Die ebene Wellengleichung kann in unserem Fall wie
folgt geschrieben werden:
Ergebnis = A * cos (2 * PI * (x / Wellenlänge - t * Frequenz));Wo:
Ergebnis - Amplitude am Punkt x zum Zeitpunkt t
A ist die maximale Amplitude
Wellenlänge - Wellenlänge
Frequenz - Wellenfrequenz
PI -
PI Nummer = 3.14159 (float)
ShaderLass uns mit den Shadern spielen. Für die "Spitze" ist die Koordinate -Z verantwortlich. Dies ist im 2D-Fall in Unity bequemer. Falls gewünscht, ist es nicht schwierig, den Shader in Y umzuschreiben.
Das erste, was wir brauchen, ist die Gleichung eines Kreises. Die Welle unseres Shaders ist symmetrisch zum Zentrum. Die Gleichung des Kreises im 2d-Fall wird beschrieben als:
r ^ 2 = x ^ 2 + y ^ 2Wir brauchen einen Radius, also hat die Gleichung die Form:
r = sqrt (x ^ 2 + y ^ 2)und dies gibt uns Symmetrie um den Punkt (0, 0) im Netz, wodurch alles auf den eindimensionalen Fall einer ebenen Welle reduziert wird.
Jetzt schreiben wir einen Shader. Ich werde nicht jeden Schritt des Schreibens eines Shaders analysieren, da dies nicht der Zweck des Artikels ist, sondern die Basis aus dem Standard Surface Shader von Unity stammt, dessen Vorlage über Create-> Shader-> StandardSurfaceShader abgerufen werden kann.
Zusätzlich werden die notwendigen Eigenschaften für die Wellengleichung
hinzugefügt :
_Frequency ,
_WaveLength und
_WaveHeight . Eigenschaft
_Timer (es wäre möglich, Zeit mit GPU zu verwenden, aber während der Entwicklung und der anschließenden Animation ist es bequemer, sie manuell zu steuern.
Wir schreiben die Funktion getHeight, um die Höhe (jetzt ist dies die Z-Koordinate) zu erhalten, indem wir die Kreisgleichung in die Wellengleichung einsetzen
Indem wir einen Shader mit unserer Wellengleichung und der Kreisgleichung schreiben, erhalten wir diesen Effekt.
Shader-CodeShader "CGDevs/Rain/RainRipple" { Properties { _WaveHeight("Wave Height", float) = 1 _WaveLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Timer("Timer", Range(0,1)) = 0 _Color ("Color", Color) = (1,1,1,1) _MainTex ("Albedo (RGB)", 2D) = "white" {} _Glossiness ("Smoothness", Range(0,1)) = 0 _Metallic ("Metallic", Range(0,1)) = 0.0 } SubShader { Tags { "RenderType"= "Opaque" } LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _MainTex; struct Input { float2 uv_MainTex; }; half _Glossiness, _Metallic, _Frequency, _Timer, _WaveLength, _WaveHeight; fixed4 _Color; half getHeight(half x, half y) { const float PI = 3.14159; half rad = sqrt(x * x + y * y); half wavefunc = _WaveHeight * cos(2 * PI * (_Frequency * _Timer - rad / _WaveLength)); return wavefunc; } void vert (inout appdata_full v) { v.vertex.z -= getHeight(v.vertex.x, v.vertex.y); } void surf (Input IN, inout SurfaceOutputStandard o) { fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color; o.Albedo = c.rgb; o.Metallic = _Metallic; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
Es gibt Wellen. Aber ich möchte, dass die Animation mit einem Flugzeug beginnt und endet. Die Sinusfunktion hilft uns dabei. Multipliziert man die Amplitude mit sin (_Timer * PI), so erhält man ein glattes Erscheinungsbild und Verschwinden der Wellen. Da _Timer Werte von 0 bis 1 annimmt und der Sinus bei Null und in PI Null ist, ist dies genau das, was Sie brauchen.
Während überhaupt nicht wie ein fallender Tropfen. Das Problem ist, dass die Wellenenergie gleichmäßig verloren geht. Fügen Sie die Eigenschaft _Radius hinzu, die für den Radius des Effekts verantwortlich ist. Und wir multiplizieren die Klemmamplitude (_Radius - rad, 0, 1) und erhalten bereits einen Effekt, der eher der Wahrheit ähnelt.
Nun, der letzte Schritt. Die Tatsache, dass die Amplitude an jedem einzelnen Punkt zu einem Zeitpunkt von 0,5 ihr Maximum erreicht, ist nicht ganz richtig. Es ist besser, diese Funktion zu ersetzen.
Dann fühlte ich mich etwas zu faul, um zu zählen, und ich multiplizierte einfach den Sinus mit (1 - _Timer) und bekam eine solche Kurve.
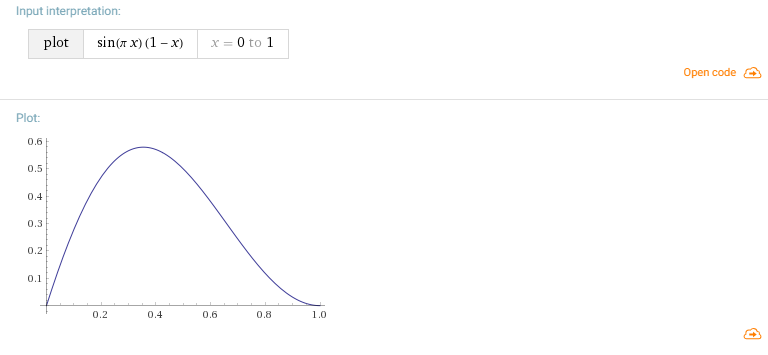
Im Allgemeinen können Sie hier aus mathematischer Sicht auch die gewünschte Kurve basierend auf der Logik auswählen, zu welchem Zeitpunkt Sie einen Peak und eine ungefähre Form wünschen, und dann an diesen Punkten eine Interpolation erstellen.
Das Ergebnis ist ein solcher Shader und Effekt.
Shader-Code Shader "CGDevs/Rain/RainRipple" { Properties { _WaveHeight("Wave Height", float) = 1 _WaveLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Radius("Radius", float) = 1 _Timer("Timer", Range(0,1)) = 0 _Color ("Color", Color) = (1,1,1,1) _MainTex ("Albedo (RGB)", 2D) = "white" {} _Glossiness ("Smoothness", Range(0,1)) = 0 _Metallic ("Metallic", Range(0,1)) = 0.0 } SubShader { Tags { "RenderType"= "Opaque" } LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _MainTex; struct Input { float2 uv_MainTex; }; half _Glossiness, _Metallic, _Frequency, _Timer, _WaveLength, _WaveHeight, _Radius; fixed4 _Color; half getHeight(half x, half y) { const float PI = 3.14159; half rad = sqrt(x * x + y * y); half wavefunc = _WaveHeight * sin(_Timer * PI) * (1 - _Timer) * clamp(_Radius - rad, 0, 1) * cos(2 * PI * (_Frequency * _Timer - rad / _WaveLength)); return wavefunc; } void vert (inout appdata_full v) { v.vertex.z -= getHeight(v.vertex.x, v.vertex.y); } void surf (Input IN, inout SurfaceOutputStandard o) { fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color; o.Albedo = c.rgb; o.Metallic = _Metallic; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
Zurück zum Thema des
vorherigen Artikels . Die Wellen werden vom Vertex-Shader implementiert, sodass das Netz des Netzes eine ziemlich große Rolle spielt. Da die Art der Bewegung bekannt ist, wird die Aufgabe vereinfacht, aber im Allgemeinen hängt das endgültige Bild von der Form des Gitters ab. Der Unterschied wird bei hoher Polygonalität unbedeutend, aber für die Leistung gilt: Je weniger Polygone, desto besser. Unten sehen Sie Bilder, die den Unterschied zwischen Gittern und Grafiken veranschaulichen.
Richtig: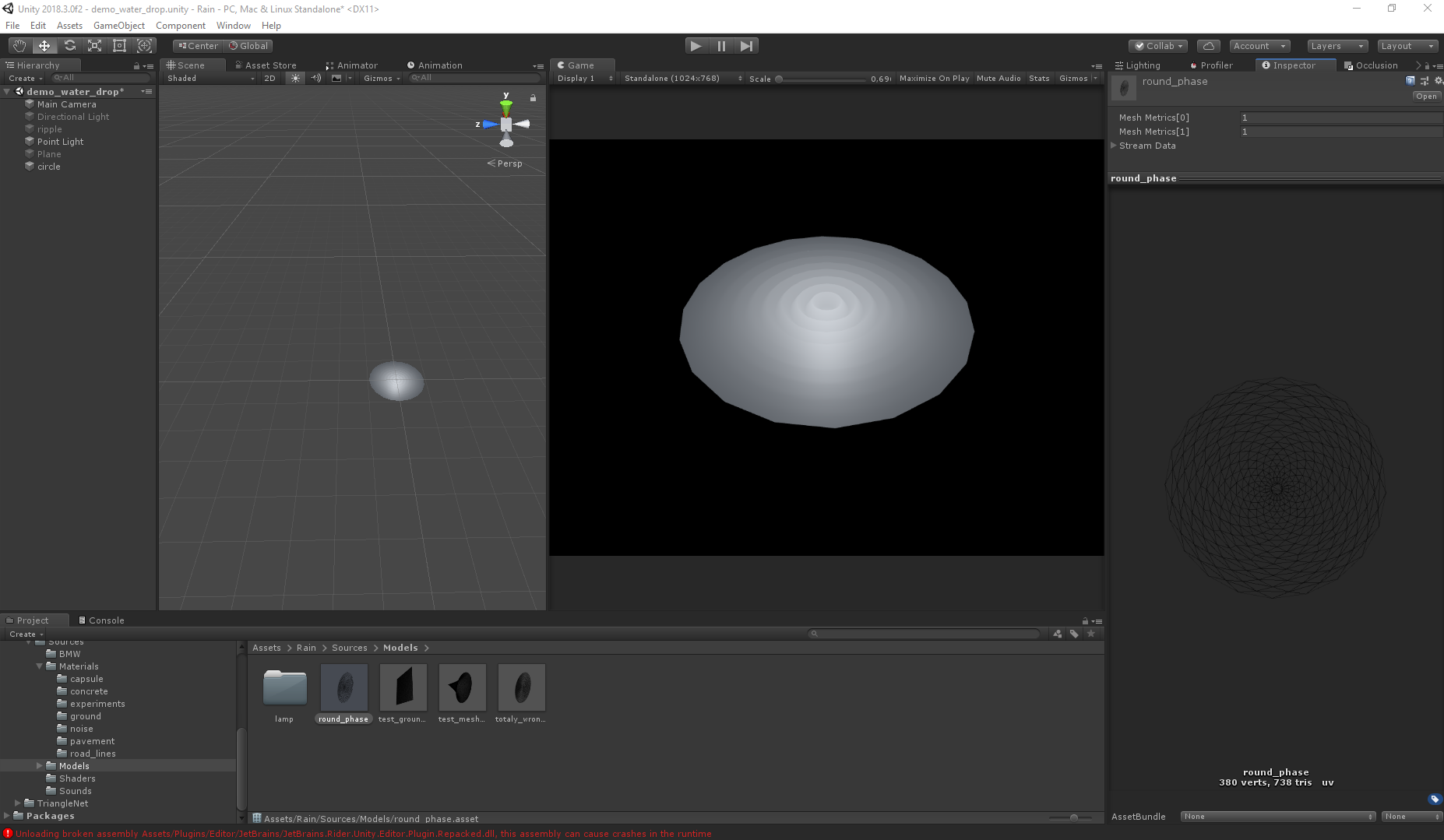
Falsch: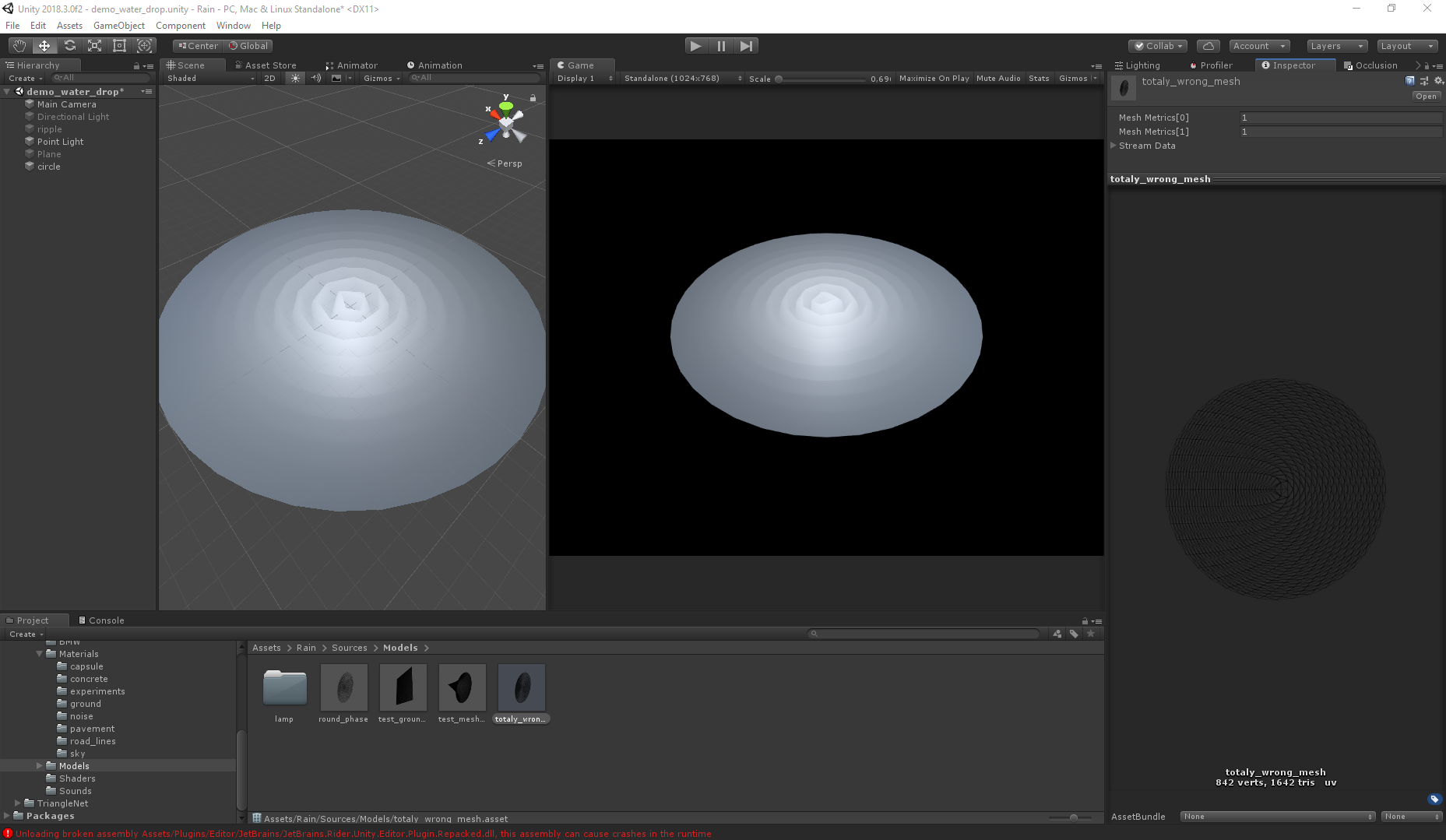
Selbst bei doppelt so vielen Polygonen ergibt das zweite Netz die falsche Darstellung (beide Netze wurden mit Triangle.Net generiert, nur mit unterschiedlichen Algorithmen).
Endgültiges BildIn einer anderen Version des Shaders wurde ein spezieller Teil hinzugefügt, um Wellen nicht ausschließlich in der Mitte, sondern an mehreren Stellen zu erzeugen. Wie dies implementiert wird und wie Sie solche Parameter übergeben können, kann ich in den folgenden Artikeln feststellen, ob das Thema interessant ist.
Hier ist der Shader selbst:
Wellenscheitel mit Stange kräuseln Shader "CGDevs/Rain/Ripple Vertex with Pole" { Properties { _MainTex ("Albedo (RGB)", 2D) = "white" {} _Normal ("Bump Map", 2D) = "white" {} _Roughness ("Metallic", 2D) = "white" {} _Occlusion ("Occlusion", 2D) = "white" {} _PoleTexture("PoleTexture", 2D) = "white" {} _Color ("Color", Color) = (1,1,1,1) _Glossiness ("Smoothness", Range(0,1)) = 0 _WaveMaxHeight("Wave Max Height", float) = 1 _WaveMaxLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Timer("Timer", Range(0,1)) = 0 } SubShader { Tags { "IgnoreProjector" = "True" "RenderType" = "Opaque"} LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _PoleTexture, _MainTex, _Normal, _Roughness, _Occlusion; half _Glossiness, _WaveMaxHeight, _Frequency, _Timer, _WaveMaxLength, _RefractionK; fixed4 _Color; struct Input { float2 uv_MainTex; }; half getHeight(half x, half y, half offetX, half offetY, half radius, half phase) { const float PI = 3.14159; half timer = _Timer + phase; half rad = sqrt((x - offetX) * (x - offetX) + (y - offetY) * (y - offetY)); half A = _WaveMaxHeight * sin(_Timer * PI) * (1 - _Timer) * (1 - timer) * radius; half wavefunc = cos(2 * PI * (_Frequency * timer - rad / _WaveMaxLength)); return A * wavefunc; } void vert (inout appdata_full v) { float4 poleParams = tex2Dlod (_PoleTexture, float4(v.texcoord.xy, 0, 0)); v.vertex.z += getHeight(v.vertex.x, v.vertex.y, (poleParams.r - 0.5) * 2, (poleParams.g - 0.5) * 2, poleParams.b , poleParams.a); } void surf (Input IN, inout SurfaceOutputStandard o) { o.Albedo = tex2D(_MainTex, IN.uv_MainTex).rgb * _Color.rgb; o.Normal = UnpackNormal(tex2D(_Normal, IN.uv_MainTex)); o.Metallic = tex2D(_Roughness, IN.uv_MainTex).rgb; o.Occlusion = tex2D(_Occlusion, IN.uv_MainTex).rgb; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
Das gesamte Projekt und seine Funktionsweise finden Sie
hier . Zwar musste ein Teil der Ressourcen aufgrund von Gewichtsbeschränkungen des Githubs (HDR Skybox und Auto) entfernt werden.
Vielen Dank für Ihre Aufmerksamkeit! Ich hoffe, der Artikel wird jemandem nützlich sein, und es wurde ein wenig klarer, warum Trigonometrie, analytische Geometrie (alles, was mit Kurven zu tun hat) und andere mathematische Disziplinen erforderlich sein können.