One Billion Queens Problem Solution oder "Untersuchung von Mustern in der Liste der Lösungen für das n-Queens-Verteilungsproblem"

Zusammenfassung

Es wird eine Beschreibung der Gesetze gegeben, die in einer sequentiellen Liste aller Lösungen für das n-Queens-Verteilungsproblem festgelegt wurden. Es wird festgestellt, dass:

• Der Anteil vollständiger Lösungen in der allgemeinen Liste aller Lösungen nimmt mit zunehmendem Wert von n ab.
  
• Komplettlösungen werden in einer sequentiellen Liste aller Lösungen so verteilt, dass Komplettlösungen, die sich in der Liste nahe beieinander befinden, am wahrscheinlichsten gefunden werden.
  
• In der allgemeinen Liste aller Lösungen gibt es Symmetrie in der Reihenfolge der vollständigen Lösungen. Wenn an der i-ten Position vom Anfang der Liste die Lösung vollständig ist, ist auch die symmetrische Lösung vom Ende der Liste an der Position n-i + 1 vollständig (die Symmetrieregel der Lösungen).
  
• Alle kurzen und vollständigen Lösungspaare, die sich symmetrisch in der Liste aller Lösungen befinden, sind komplementär - die Summe der Positionsindizes der entsprechenden Linien ist konstant und gleich n + 1 (die Regel der Komplementarität von Lösungen). Dies deutet darauf hin, dass nur die erste Hälfte der Liste aller vollständigen Lösungen „eindeutig“ ist. Jede vollständige Lösung aus der zweiten Hälfte der Liste kann auf der Grundlage der Komplementaritätsregel erhalten werden. Eine Konsequenz dieser Regel ist die Tatsache, dass für jeden Wert von n die Anzahl der vollständigen Lösungen immer eine gerade Zahl ist.
  
• Die Aktivität der Zellen der Zeilen der Lösungsmatrix ist symmetrisch in Bezug auf die horizontale Achse, die durch die Mitte dieser Matrix verläuft. Dies bedeutet, dass die Aktivität der Zellen der i-ten Reihe immer mit der Aktivität der Zellen der Reihe n-i + 1 übereinstimmt. Mit Aktivität ist die Häufigkeit gemeint, mit der der Zellindex in der entsprechenden Zeile der Liste der vollständigen Lösungen auftritt. In ähnlicher Weise ist die Aktivität der Zellen der Spalten der Lösungsmatrix symmetrisch um die vertikale Achse, die die Matrix in zwei gleiche Teile teilt
  
• Unabhängig von n erscheint bei einer sequentiellen Suche aller Lösungen die erste vollständige Lösung erst nach einer bestimmten Folge von kurzen Lösungen. Die Größe der anfänglichen Folge von kurzen Lösungen nimmt mit n zu. Die Länge der Liste der kurzen Lösungen vor dem Erscheinen der ersten vollständigen Lösung für gerade Werte von n ist signifikant länger als für die nächsten ungeraden Werte.
  
• Die Linie in der Entscheidungsmatrix, auf der sich Schwierigkeiten vorwärts zu bewegen beginnen und die erste kurze Entscheidung gebildet wird, teilt die Matrix gemäß der Golden-Ratio-Regel. Für kleine Werte von n ist eine solche Schlussfolgerung ungefähr, jedoch steigt mit einer Erhöhung des Wertes von n die Genauigkeit einer solchen Schlussfolgerung asymptotisch auf das Niveau der Standardregel.
  

Diese Veröffentlichung präsentiert die wichtigsten Ergebnisse des Artikels [1] , der in der Zeitschrift „Modeling of Artificial Intelligence, 2018, 5 (1)“ veröffentlicht wurde. Auf Habré gab es Arbeiten, die mit einem Problem von n-Queens verbunden waren: [2] , [3] ,
Das Problem, n Königinnen auf einem Schachbrett in nxn-Größe zu verteilen, hat eine lange Geschichte. Es wurde ursprünglich 1848 von M. Bezzel [4] als intellektuelle Aufgabe für ein reguläres Schachbrett formuliert. Im Laufe der Zeit wurde die Erklärung des Problems von F. Nauck [5] erweitert, und die Größe eines Schachbretts konnte jeden Wert annehmen.

Einführung

Die Erklärung des Problems ist recht einfach: Sie müssen n Königinnen auf einem Schachbrett der Größe nxn verteilen, sodass in jeder Zeile, jeder Spalte sowie auf der linken und rechten Diagonale, die durch die Zelle verläuft, in der sich die Königin befindet, nicht mehr als eine Königin vorhanden ist. Diese Aufgabe ist leicht zu verstehen oder jemandem zu erklären, aber es ist ziemlich schwierig, sie zu lösen. Tatsache ist, dass es keine Regeln gibt, auf deren Grundlage Sie Königinnen in jeder Zeile anordnen können, um eine Lösung zu erhalten. Eine Lösung kann nur erhalten werden, indem verschiedene Varianten der Anordnung von Königinnen in bestimmten Zeilen aufgezählt werden. Die Komplexität dieser Lösungsmethode liegt jedoch darin, dass die Anzahl aller Varianten der Anordnung von Königinnen mit zunehmendem n exponentiell zunimmt. Wenn Sie einen Schritt nach vorne machen, um die Königin in die freie Position einer bestimmten Zeile zu bringen, ändert sich außerdem die Liste der freien Positionen in den verbleibenden Zeilen. Wenn Sie einen Schritt zurückgehen, müssen Sie die Spuren zuvor ausgeführter Aktionen löschen, um einen Suchzweig zu bilden.

Es gibt eine große Anzahl von Veröffentlichungen, die sich auf verschiedene Aspekte der Lösung des n-Queens-Problems beziehen. Sie können mehreren Forschungsbereichen zugeordnet werden: der Suche nach allen vollständigen Lösungen für einen bestimmten Wert der Größe eines Schachbretts (n), der Entwicklung eines schnellen Algorithmus zum Finden einer Lösung für verschiedene Werte von n, der Lösung des vollständigen Problems zu einer vollständigen Lösung, für eine beliebige Zusammensetzung von k Königinnen, Fragen die rechnerische Komplexität algorithmischer Berechnungen sowie verschiedene Modifikationen der ursprünglichen Formulierung des Problems. Um diese Bereiche kennenzulernen, würde ich interessante Veröffentlichungen von B. Jordan, S. Brett [6] und IP Gent, C. Jefferson, P. Nightingale [7] empfehlen, die einen ziemlich detaillierten Überblick über verschiedene Forschungsbereiche bieten. Besonders hervorzuheben ist die von Walter Costers unterstützte Online-Publikation [8] , die von einer Gruppe der Universität Leiden erstellt wurde und Links zu 342 Publikationen zum Problem der n-Königinnen enthält (Stand Dezember 2018).

Obwohl das n-Queens-Problem seit mehr als 150 Jahren aktiv ist und in dieser Zeit eine große Anzahl von Veröffentlichungen erschienen ist, konnte ich keinen Job finden, der für die Suche nach Mustern in den Ergebnissen der Lösung dieses Problems relevant wäre. Die meisten Projekte im Zusammenhang mit der Suche nach allen Lösungen haben die gefundenen Lösungen höchstwahrscheinlich nicht gespeichert und nicht gesehen, was sich „im Inneren“ befindet. In der Aufgabenstellung gab es andere dominierende Ziele, und unsere geschätzten Kollegen haben sie erreicht. Aus der Ferne schien es mir jedoch ähnlich zu sein, als würde eine Person Eier zum Frühstück kochen, sie aber nicht essen, sondern wegwerfen und nur die Anzahl der gekochten Eier in seinem Gedächtnis belassen. Ich war mir immer sicher, dass wenn die Daten nicht zufällig sind, sie eine gewisse Regelmäßigkeit aufweisen sollten, wenn selbst wir diese Regelmäßigkeit nicht finden können. Diese Überzeugung war der Grund für die Suche nach Mustern in dieser Aufgabe.

Neben dem Wunsch, den Mitgliedern der Habr-Community nützliche Informationen zum Nachdenken zu liefern, möchte ich, dass talentierte Programmierer, von denen die meisten auf Habr sind, einer Entwicklungsrichtung wie der Computersimulation (Computersimulation) mehr Aufmerksamkeit schenken. Als Forschungsmethode wird diese "Algorithmische Mathematik" in vielen Bereichen an der "Spitze" eingesetzt: Künstliche Intelligenz, Software-Wissenschaft, Datenwissenschaft ... und ich bin sicher, dass sehr komplexe und wichtige Probleme für die praktische Anwendung auf der Grundlage der algorithmischen Mathematik gelöst werden sonst.

Definitionen

Im Folgenden bezeichnen wir die Größe des Schachbretts mit dem Symbol n. Eine Lösung wird als vollständig bezeichnet, wenn alle n Königinnen konsistent auf einem Schachbrett platziert sind. Alle anderen Lösungen, wenn die Anzahl der korrekt platzierten Königinnen weniger als n beträgt, werden wir kurze Lösungen nennen. Mit der Länge einer Lösung meinen wir die Anzahl (k) der korrekt platzierten Königinnen. Die Anzahl aller Lösungen für einen gegebenen Wert von n wird mit m bezeichnet. Als Analogon zu einem "Schachbrett" der Größe nx n. Betrachten wir eine "Lösungsmatrix" der Größe nx n.

Starten Sie

Um eine Studie durchzuführen, wurde ein Algorithmus entwickelt, um nach allen Lösungen für einen beliebigen Wert von n zu suchen. Wir haben keine Standardrekursion oder das übliche System verschachtelter Schleifen verwendet. Für große Werte von n wäre ein solcher Ansatz ziemlich problematisch. Der Algorithmus wurde auf der Grundlage einer Reihe von interagierenden Ereignissen erstellt, in denen jeweils ein bestimmtes System von Aktionen stattfindet, die miteinander verbunden sind. Dies ermöglicht es, den Mechanismus zum Ändern des Zustandsraums einfach zu implementieren, wenn der nächste Knoten im Zweig der Problemlösung ausgewählt wird (Vorwärtsverfolgung) oder die Spuren zuvor ausgeführter Aktionen gelöscht werden, wenn ein oder mehrere Schritte zurückgegeben werden (Rückverfolgung). Es gibt keine besonderen Anforderungen an die Speichergröße oder die Prozessorgeschwindigkeit im Algorithmus.

Basierend auf diesem Algorithmus wurden alle sequentiellen Lösungen (sowohl kurz als auch vollständig) für verschiedene Werte der Lösungsmatrix n = (7, ..., 16) gefunden. Da die Größe der Liste der vollständigen Lösungen der benannten Sequenz The On-Line Encyclopedya of Integer Sequences (Sequenz A000170 [9]) entspricht und in vielen Veröffentlichungen angegeben ist, erscheint es mir interessant, die Größe der Liste aller Lösungen (kurz + vollständig) für die von uns berücksichtigten Werte von n aufzulisten: 7 (194), 8 (736), 9 (2 936), 10 (12 774), 11 (61 076), 12 (314 730), 13 (1 716 652), 14 (10 030 692), 15 ( 62 518 772), 16 (415 515 376).

Unter Verwendung der gefundenen Lösungen geben wir den Wortlaut einiger Probleme, Methoden zu ihrer Lösung und eine Beschreibung der Ergebnisse.

1. Der Zustandsraum, in dem nach Lösungen gesucht wird

Die Aufzählung verschiedener Optionen für die Anordnung von Königinnen in bestimmten Zeilen einer Matrix einer Entscheidung der Größe n führt zur Bildung eines Zustandsraums. Wenn es keine Verbote für die Anordnung von Königinnen in der einen oder anderen Zelle der Matrix gäbe, wäre die Größe des Zustandsraums n ⁿ . Wenn wir nur die Regel berücksichtigen, die die Position von mehr als einer Königin in jeder Zeile und jeder Spalte verbietet, erhalten wir eine Teilmenge des Zustandsraums, dessen Größe gleich n ist! Diese Teilmenge des Zustandsraums entspricht dem Problem der Verteilung von n durch den Turm. Wenn wir dabei auch die Regel berücksichtigen, die die Position von mehr als einer Königin auf der linken und rechten Diagonale verbietet, die durch die Zelle verläuft, in der sich die Königin befindet, erhalten wir einen Suchraum, dessen Größe kleiner als n ist! Wir nennen eine solche Teilmenge des Zustandsraums - ein produktiver Suchraum, basierend auf der Tatsache, dass nur in diesem Unterraum alle möglichen Lösungen sind. Alle abgeschlossenen Zweige im produktiven Suchraum sind Lösungen mit einer bestimmten Anzahl korrekt platzierter Königinnen. Grundsätzlich handelt es sich um kurze Entscheidungen, und nur ein kleiner Teil davon sind vollständige Entscheidungen.

Abbildung 1 zeigt Diagramme des natürlichen Logarithmus von drei Indikatoren: a) den Fakultätswert (n!) Zur Größe der Entscheidungsmatrix; b) die Anzahl aller Entscheidungen (sowohl kurz als auch vollständig); c) die Anzahl der vollständigen Lösungen in Abhängigkeit von der Größe der Lösungsmatrix (n). Wie erwartet sind alle Kurven durch einen exponentiellen Anstieg mit zunehmendem n gekennzeichnet. Die Wachstumsraten der Anzahl aller Lösungen und der Anzahl der vollständigen Lösungen unterscheiden sich, obwohl dies in der Grafik aufgrund der geringen Stichprobengröße von n Werten nicht so deutlich erkennbar ist. Beispielsweise beträgt für n = 13 die Differenz zwischen den Logarithmen dieser Indikatoren 3,148, und für n = 16 erhöht sich diese Differenz um 0,190 und beträgt 3,338. Offensichtlich wird diese Diskrepanz mit einem weiteren Anstieg von n signifikanter sein.

Abb. 1 Abhängigkeit des Logarithmus von der Größe des Zustandsraums vom Wert n

2. Wie ändert sich der Anteil vollständiger Entscheidungen in der allgemeinen Liste aller Entscheidungen?

Wenn die Wachstumsrate der Anzahl der vollständigen Lösungen hinter der Wachstumsrate der Anzahl aller Lösungen zurückbleibt, nimmt die Wahrscheinlichkeit, eine vollständige Lösung in der allgemeinen Liste aller Lösungen zu finden, mit zunehmendem Wert von n ab. Abbildung 2 zeigt eine grafische Darstellung des Anteils vollständiger Lösungen in der allgemeinen Liste aller Lösungen zum Wert von n. Es ist ersichtlich, dass mit zunehmender Größe der Lösungsmatrix der Anteil aller vollständigen Lösungen in der allgemeinen Liste abnimmt. Für die Anfangswerte n = (7, ..., 14) nimmt dieser Wert 5,66-mal von 0,2062 auf 0,0364 ab, und dann setzt sich eine allmähliche asymptotische Abnahme dieses Wertes fort. Hier entsteht ein formaler Widerspruch zwischen zwei Aussagen: Einerseits nimmt die Anzahl der vollständigen Lösungen mit zunehmendem n exponentiell zu, andererseits nimmt die Wahrscheinlichkeit einer vollständigen Lösung in einer sequentiellen Liste aller Lösungen ständig ab. Dieses scheinbare Paradoxon wird sehr einfach erklärt: Die Größe des Produktivraums und die damit verbundene Größe der Liste aller Lösungen wächst mit zunehmendem n schneller als die Anzahl der vollständigen Lösungen. Dies ist wie der Versuch, eine Nadel im Heuhaufen zu finden - die Menge an Heu "mit zunehmendem n" wächst schneller als die Anzahl der Nadeln, die dort verloren gehen. Daher können wir annehmen, dass, wenn für n = 27 die Anzahl der vollständigen Lösungen ungefähr 2,346 * 10 ¹⁷ beträgt, der entsprechende Wert der Anzahl aller Lösungen höchstwahrscheinlich 3-4 Größenordnungen größer als ~ 10 ^{20 ist}

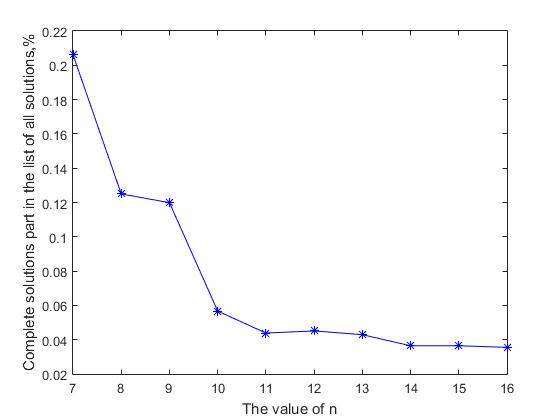
Abb. 2 Verringerung des Anteils an Komplettlösungen in der allgemeinen Liste aller Lösungen mit zunehmendem n

3. Wie häufig sind Lösungen unterschiedlicher Länge in der Liste aller Lösungen?

Wie bereits erwähnt, sind alle abgeschlossenen Zweige im produktiven Suchraum Lösungen mit einer unterschiedlichen Anzahl korrekt platzierter Königinnen.
Es ist für uns von Interesse, mit welcher Häufigkeit Lösungen unterschiedlicher Länge in der allgemeinen Liste aller Lösungen enthalten sind.

Tabelle 1 für die Werte n = (7, ..., 12) zeigt die entsprechenden Werte der relativen Häufigkeiten für Lösungen mit unterschiedlichen Längen. Die entsprechende visuelle Darstellung dieser Daten ist in Abbildung 3 dargestellt.

Die Analyse der Tabelle ermöglicht es uns, die folgenden Schlussfolgerungen zu ziehen:

a) Für jede Matrix der Größe n gibt es eine bestimmte Länge der Lösung mit einer maximalen Häufigkeit (fett hervorgehoben).

Tabelle 1. Relative Häufigkeit (%) von Lösungen unterschiedlicher Länge (k) für eine Matrix der Größe n = (7, ..., 12)

n \ k	4	5	6	7	8	9	10	11	12
7	10.31	31.23	27,84	20.62
8	2.45	20.38	34,78	29,89	12.50
9	0,34	5.79	21.73	35,83	34.32	11.99
10	0,05	1,35	8.41	25.62	32,94	25,96	5.67
11		0,15	2.12	11.80	26.71	34.47	20.36	4.39
12		0,01	0,29	3.28	13.56	29,88	31.29	17.18	4.51

b) Mit zunehmendem n nimmt die Anzahl der Lösungen mit unterschiedlichen Längen zu. Dementsprechend nimmt die relative Häufigkeit aller Entscheidungen ab.

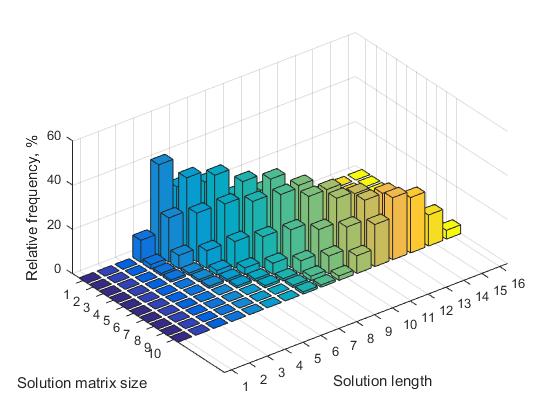
Abb. 3 Häufigkeit von Lösungen unterschiedlicher Länge in Abhängigkeit von der Größe der Lösungsmatrix, n = 7, ..., 16

c) Für jede Matrix der Größe n gibt es eine bestimmte Mindestgröße der Länge der Lösung, unterhalb derer keine kurzen Lösungen auftreten. Mit zunehmendem n steigt der Wert dieser Schwelle. Zum Beispiel ist für n = 8 der Schwellenwert 4 bzw. für n = 16 ist der Schwellenwert 7.

4. Wie ist die relative Anordnung von Komplettlösungen in einer sequentiellen Liste aller Lösungen?

In der Erklärung des Problems "zur Verteilung von n Königinnen" gibt es keine Gründe, die Anlass geben würden, eine Annahme über die Reihenfolge der vollständigen Entscheidungen in der allgemeinen Liste aller Lösungen zu treffen. Wir waren daran interessiert, ob die vollständigen Lösungen in der allgemeinen Liste gleichmäßig, zufällig verteilt sind oder ob sie einige Besonderheiten aufweisen. Um dies herauszufinden, haben wir die Abstände zwischen den nächsten vollständigen Lösungen in einer sequentiellen Liste aller Lösungen analysiert. Wie aus 4 ersichtlich ist, ist für n = 12 ein Diagramm der Änderungen der entsprechenden Frequenzen dargestellt.

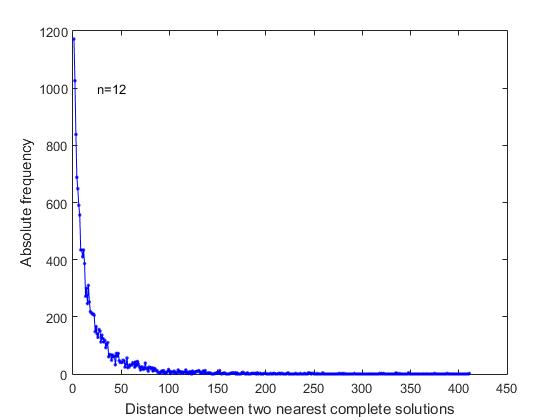
Abb. 4 Häufigkeit gegen Abstand zwischen den nächsten vollständigen Lösungen in einer sequentiellen Liste aller vollständigen Lösungen (n = 12)

Mit der größten Häufigkeit gibt es vollständige Lösungen, die in einer gemeinsamen sequentiellen Liste aller Lösungen unmittelbar aufeinander folgen. Dies sind die Fälle der Bildung des Suchzweigs, wenn die Beziehung der freien Positionen in den letzten Zeilen es Ihnen ermöglicht, zwei oder mehr aufeinanderfolgende vollständige Lösungen zu bilden. Die maximale Häufigkeit sind ferner die vollständigen Lösungen, zwischen denen sich befinden: eine kurze Lösung, zwei kurze Lösungen usw.

5. Gibt es ein Muster bei der Anordnung vollständiger Lösungen in der allgemeinen Liste aller Lösungen?

Um diese Frage zu beantworten, haben wir sequentielle Listen aller Lösungen für die Werte n = (7, ..., 16) analysiert. Um die Ergebnisse in 5 für den Wert n = 8 klar zu demonstrieren, wird ein Diagramm dargestellt, in dem die Länge jeder Lösung in der Liste aller 736 Lösungen nacheinander angegeben ist. Hier sind nur 92 Lösungen vollständig und sie sind rot hervorgehoben, die restlichen 644 Lösungen sind kurz und blau hervorgehoben. Es ist ersichtlich, dass die Komplettlösungen in der Liste aller Lösungen nicht gleichmäßig verteilt sind. Es gibt Bereiche, in denen Komplettlösungen häufiger vorkommen, und es gibt Bereiche, in denen Komplettlösungen selten oder gar nicht sind.

Abb. 5 Die Länge jeder Lösung in einer sequentiellen Liste aller Lösungen für eine 8 x 8-Matrix (rot - vollständige Lösungen, blau - kurze Lösungen). Die Gesamtzahl aller Lösungen beträgt 736

Hier ist jedoch noch etwas anderes wichtig. Wenn Sie sich das Bild genau ansehen, das einem blau-roten Barcode ähnelt, werden Sie ein sehr wichtiges Merkmal bemerken: Alle roten Linien sind symmetrisch in Bezug auf eine bedingte vertikale Linie, die durch die Mitte der Liste der Lösungen verläuft. In der Tat, wie die Prüfung zeigt, wird im Schritt m-i + 1 sicher eine vollständige Lösung gefunden, wenn im i-ten Schritt vom Anfang der allgemeinen Liste eine vollständige Lösung vorhanden ist. Wenn beispielsweise für n = 8 die erste vollständige Lösung in der sequentiellen Suche nach allen Lösungen in Schritt 43 angezeigt wird, wird die letzte vollständige Lösung in der Liste dementsprechend in Schritt 736–43 + 1 = 694 gefunden. Wenn die 17. Lösung für eine 10x10-Matrix in Schritt 368 in der Liste angezeigt wird, wird die dazu symmetrische vollständige Lösung in Schritt 12774-17 + 1 = 12407 in der Liste aller Lösungen angezeigt. Diese Regel gilt für eine Entscheidungsmatrix beliebiger Größe. Daher können wir eine Regel formulieren. Wenn für jeden Wert von n in der sequentiellen Liste aller Lösungen an der i-ten Position vom Anfang der Liste die Lösung vollständig ist, ist auch die symmetrische Lösung vom Ende der Liste an Position m-i + 1 vollständig (die Symmetrieregel der Lösungen). m, , . , n, , . ( – ).

, – . n+1 . , 17- n=10 368- (1, 5, 7, 10, 4, 2, 9, 3, 6, 8).

, 12407 (10, 6, 4, 1, 7, 9, 2, 8, 5, 3). , (11, 11, …,11). n, , , . . n, ( , ), , – n+1 ( ). Q(i ) Q1(i) – ,

<b>`Q ( i ) + Q1 ( i ) = n + 1, i = (1, n) `</b> 

Diese Regel bedeutet, dass, wenn im i- ten Schritt eine vollständige Lösung erhalten wird, die symmetrische vollständige Lösung im Schritt m - i + 1 bekannt wird . Daher reicht es bei der Suche nach allen Komplettlösungen aus, nur die erste Hälfte aller Komplettlösungen zu finden. Die zweite Hälfte der Liste der vollständigen Lösungen kann aus den bereits erhaltenen Lösungen auf der Grundlage der Komplementaritätsregel bestimmt werden. Das Kriterium, dass die Hälfte der Liste der vollständigen Lösungen erreicht wird, ist die Erfüllung der Komplementaritätsregel zwischen der vorherigen vollständigen Lösung Q (i-1) und dem nachfolgenden Q (i) . es ist notwendig, dass die Summe jedes Paares entsprechender Indizes von zwei aufeinanderfolgenden Lösungen gleich n + 1 ist . Da jede vollständige Lösung aus der Liste aller vollständigen Lösungen eindeutig ist, ergänzen sich nur die aufeinander folgenden vollständigen Lösungen, die sich auf beiden Seiten der Grenze befinden, die die Liste in zwei Hälften teilt.

Diese beiden Regeln werden es in Zukunft ermöglichen, bei der Suche nach allen vollständigen Lösungen für einen nächsten Wert von n den Rechenaufwand und dementsprechend die Berechnungszeit um die Hälfte zu reduzieren.

6. Visualisierung der Abfolge der Schritte zum Finden der ersten vollständigen Lösung

Wie werden die Schritte vorwärts (Vorwärtsverfolgung) und zurück (Rückverfolgung) ausgeführt, wenn ein Zweig einer Lösungssuche gebildet wird? Um diese Frage zu beantworten, haben wir für eine 10 x 10-Matrix die Reihenfolge der ersten 194 Übergänge zwischen den Linien bestimmt, bis die erste vollständige Lösung erscheint. Das entsprechende Diagramm ist in Abbildung 6 dargestellt. Blaue Linien zeigen eine Vorwärtsbewegung an und rote Linien zeigen eine Rückkehr an. In diesen 194 Schritten wurden 35 kurze Lösungen erstellt. Die Abbildung zeigt, dass die meisten Übergänge (84,5%) zwischen den Linien (5, 6, 7, 8) auftreten. Dies ist eine Art „Engpass“ auf dem Weg zum „Ziel“. Wie aus der Abbildung hervorgeht, gibt es nur 7 Fälle des Wechsels in die 4. Zeile und einen Fall des Wechsels in die dritte Zeile. Es gibt auch 13 Fälle, in denen auf die 9. Zeile umgeschaltet wird. Drei Versuche, in die 10. Zeile zu wechseln, waren erfolglos, da in diesen Suchzweigen in der 10. Zeile keine leere Position vorhanden war. Dieses Beispiel zeigt alle Zweige von short

Abb. 6 Visualisierung von Backtracking- (rot) und Forwardtracking-Ereignissen (blau) für die ersten 194 Suchschritte (n = 10)

Lösungen, bis zur ersten vollständigen Lösung. Jeder Algorithmus zur Lösung eines solchen Problems ist effektiv, wenn er einen Mechanismus enthält, der alle (oder einen Teil) der Zweige eliminiert, die zu kurzen Lösungen führen.

7. Nach wie vielen kurzen Entscheidungen erscheint die erste vollständige Lösung?

Angesichts der Tatsache, dass vollständige Lösungen in verschiedenen Teilen der Liste aller Lösungen unterschiedlich angezeigt werden, scheint es wichtig zu sein, herauszufinden, in wie vielen kurzen Lösungen die erste vollständige Lösung angezeigt wird, wenn alle Lösungen nacheinander durchsucht werden. Zu diesem Zweck wurden für die Werte n = (7, ..., 35) alle kurzen Lösungen nacheinander bis zum Auftreten der ersten vollständigen Lösung berechnet. Wie aus 7 ersichtlich ist, die ein Diagramm der Abhängigkeit von n, dem natürlichen Logarithmus der Schrittnummer, zeigt, wenn die erste vollständige Lösung erschien, erscheint für gerade Werte von n die erste vollständige Lösung viel später als für die nächsten ungeraden Werte von n. Beispielsweise erscheint für einen ungeraden Wert n = 21 die erste vollständige Lösung in Schritt 3138, und für den nächsten geraden Wert n = 22 erscheint die erste vollständige Lösung in Schritt 628169. Dementsprechend erscheint für den nächsten ungeraden Wert n = 23 die erste vollständige Lösung in Schritt 9155.

Abb. 7 Die Anzahl der kurzen Lösungen bis zur ersten vollständigen Lösung für verschiedene Werte von n

Die Anzahl der Iterationsschritte für gerade n = 22 ist 200,2- bzw. 68,6-mal höher als die nächsten ungeraden Werte. Dies zeigt sich insbesondere in der Zählzeit für n = 34. Hier erscheint die erste vollständige Lösung bei 826 337 184. Schritten und für die nächsten ungeraden Zahlen (33, 35) bei 50 704 900. bzw. 84 888 759 Schritten. Es sollte auch über die Verletzung des monotonen Wachstums der Anzahl von kurzen Lösungen vor dem Auftreten der ersten vollständigen Lösung mit zunehmendem n gesagt werden. Für gerade Werte von n tritt dies bei n = 19 auf, für ungerade Werte bei n = 24 und n = 26.

8. Ist die Zellenfrequenz jeder Zeile in der Liste aller Komplettlösungen gleich?

Die nxn-große Entscheidungsmatrix, die als Analogon eines Schachbretts dient, ist wie eine Szene, in der alle Ereignisse stattfinden. Jede in dieser Szene gebildete vollständige Lösung besteht aus Indizes von Zellen verschiedener Zeilen, weil Jede solche Zelle ist ein Knoten im Lösungssuchzweig. Die Frage, die uns interessieren wird, lautet wie folgt: Ist die Last in jeder Zeile für verschiedene Zellen gleich, wenn eine Liste aller vollständigen Lösungen erstellt wird? Je höher der Frequenzwert ist, desto höher ist natürlich die Aktivität dieser Zelle bei der Erstellung einer Liste vollständiger Lösungen. Um dies festzustellen, bestimmen wir für jede Zeile anhand einer Liste aller vollständigen Lösungen die relative Häufigkeit der verschiedenen Indizes. Zunächst analysieren wir eine Lösungsmatrix der Größe n = 8. Untersuchen wir jede Zeile des Arrays vollständiger Lösungen nacheinander und bestimmen die Häufigkeit verschiedener Indexwerte. Tabelle 2 zeigt die entsprechenden Werte der absoluten Aktivitätsfrequenzen verschiedener Zellen in jeder der acht Reihen und in Fig. 1. 8

Tabelle 2. Absolute Häufigkeit der Zellaktivität in jeder der acht Zeilen der 8x8-Entscheidungsmatrix, basierend auf einer Analyse der Liste aller vollständigen Lösungen

row \ col	1	2	3	4	5	6	7	8
1	4	8	16	18	18	16	8	4
2	8	16	14	8	8	14	16	8
3	16	14	4	12	12	4	14	16
4	18	8	12	8	8	12	8	18
5	18	8	12	8	8	12	8	18
6	16	14	4	12	12	4	14	16
7	8	16	14	8	8	14	16	8
8	4	8	16	18	18	16	8	4

Es wird eine Gruppe von 4 Diagrammen dargestellt, wobei jedes Diagramm die Änderung der relativen Häufigkeiten innerhalb einer Linie charakterisiert. Eine der grundlegend wichtigen Schlussfolgerungen, die aus der Analyse aller erhaltenen Daten gezogen werden können, lautet wie folgt:

• für eine Entscheidungsmatrix beliebiger Größe n fällt die Aktivität der Zellen der i- ten Reihe mit der Aktivität der Zelle n-i + 1 zusammen , d.h. Die Aktivität der Zellen der ersten Reihe stimmt immer mit der Aktivität der Zellen der letzten Reihe überein. Die Aktivität der Zellen der zweiten Reihe stimmt mit der Aktivität der Zellen der vorletzten Reihe überein.
  
  Wenn n ungerade ist, hat nur die mittlere Zeile der Lösungsmatrix kein symmetrisches Paar, für alle anderen Zellen gilt die obige Regel
• Wir nennen dies die "Eigenschaft der horizontalen Symmetrie der Aktivität der Zellen verschiedener Zeilen der Lösungsmatrix" . Aus diesem Grund haben wir nur 4 Diagramme für die Entscheidungsmatrix der Größe n = 8 dargestellt, da die entsprechenden Diagramme der Zellaktivität für die Zeilen (1, 8), (2.7), (3.6) und (4.5) vollständig identisch sind.

Es sollte auch beachtet werden, dass die Frequenzwerte symmetrisch um die vertikale Achse sind, die die Matrix in zwei gleiche Teile teilt (im Fall eines geraden Wertes von n) oder durch die Medianspalte geht (im Fall eines ungeraden Werts von n). Wir nennen dies die "vertikale Symmetrieeigenschaft der Aktivität der Zellen verschiedener Zeilen der Lösungsmatrix" .

Zusätzlich sind, wie aus der Analyse von Tabelle 2 hervorgeht, die Frequenzen in der Lösungsmatrix in Bezug auf die linke und rechte Hauptdiagonale symmetrisch.

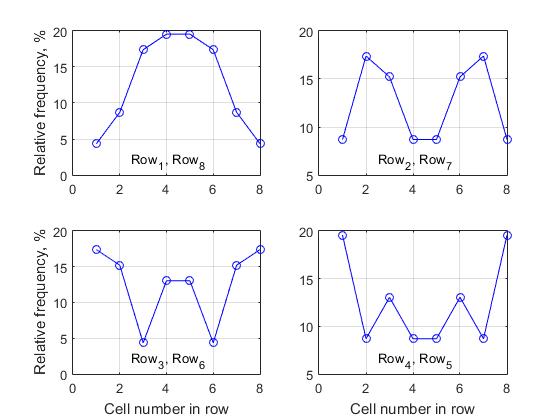
Fig. 8 Zellaktivität der entsprechenden Zeilen bei der Bildung der Liste der vollständigen Lösungen, n = 8

Ich denke, dass das Vorhandensein restriktiver Regeln in der Problemstellung und die damit verbundene Eigenschaft des Nichtdeterminismus eine Art harmonische Beziehung zwischen Knoten in verschiedenen Linien „bilden“. Die Zweige der Suche, die in diese Regeln passen, führen zur Bildung einer vollständigen Lösung. Die verbleibenden Zweige der Suche verstoßen irgendwann gegen diese Regeln und „schließen ihre Reise ab“ in Form von kurzen Entscheidungen. Hierbei ist zu beachten, dass die Zellen der Entscheidungsmatrix nur eine lokale Beziehung innerhalb der Projektionseinflussgruppe haben, es gibt keine vorgeschriebenen Regeln für koordinierte Aktionen zwischen ihnen. Die kollektive Aktivität der Zellen ist nur eine Folge des Einflusses restriktiver Regeln. Daher bleibt eine interessante Frage offen, wie sich restriktive Regeln wie Nichtdeterminismusfaktoren auf die Zellen der Entscheidungsmatrix auswirken, was letztendlich zur Bildung einer „harmonischen“ Zellaktivitätsmatrix führt - symmetrisch in Bezug auf die horizontale und vertikale Achse sowie in Bezug auf die linke und rechte Hauptdiagonalen. Ist dies eine charakteristische Eigenschaft nur dieses Problems oder gilt es auch für andere nicht deterministische Probleme?

9. Ab welcher Zeilennummer wird der Forward Tracking - Back Tracking-Algorithmus aktiviert?

Wenn wir der Operation des sequentiellen Zeilenauswahlalgorithmus in der Entscheidungsmatrix für den Standort der Königin folgen, können wir sehen, dass ab einer bestimmten Zeile, die wir "StopRow" nennen, der Prozess des Vorwärtsbewegens "gebremst" wird. In der Suchbranche ist dies die erste Zeile, in der Probleme mit der Verfügbarkeit von kostenlos auftreten

Abb. 9-1 Abhängigkeit des Verhältnisses des StopRow-Index zu n von der Größe der Entscheidungsmatrix (Teil-1)

Position für den Standort der Königin. Ab dieser Zeile wird der Back-Tracking-Algorithmus aktiviert, um die Spuren zuvor ausgeführter Aktionen zu löschen und zurückzukehren. Dies ist die Zeile, in der die erste kurze Lösung angezeigt wird.

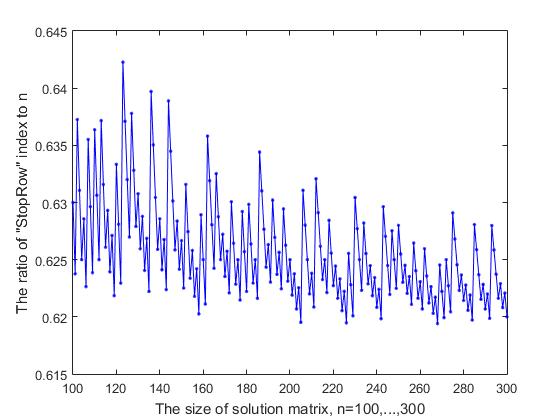
Abb. 9-2 Abhängigkeit des Verhältnisses des StopRow-Index zu n von der Größe der Entscheidungsmatrix (Teil-2)

Der Index der Zeile „StopRow“, mit dem sich Schwierigkeiten vorwärts bewegen, hängt von der Größe n der Entscheidungsmatrix ab. Wenn wir das Verhältnis dieses Index, das wir mit StopInd bezeichnen, zur Größe der Lösungsmatrix n betrachten, schwankt dieses Verhältnis, wie aus Abbildung 9-1 ersichtlich, in der die Berechnungsergebnisse für die Anfangswerte n = (7, ..., 99) dargestellt sind, mehr oder weniger stark Seite und neigt dazu, abzunehmen. Mit einer Zunahme von n = (100, ..., 300) schwankt dieses Verhältnis zwischen 0,619 und 0,642 (Abb. 9-2), und mit einer weiteren Zunahme von n erhalten wir die folgenden Ergebnisse (die Werte von n sind nacheinander angegeben und der Wert in Klammern ist StopInd- und StopInd / n-Verhältnis: 1000 (619, 0,6190), 2000 (1239, 0,6195), 3000 (1856, 0,6187), 4000 (2473, 0,6182), 5000 (3091, 0,6182). Überraschenderweise kann argumentiert werden, dass stop -line teilt die Entscheidungsmatrix gemäß der Golden- Ratio- Regel : Das StopInd / n- Verhältnis unterscheidet sich von (n-StopInd) / StopInd um einen kleinen Betrag, der mit zunehmendem n gegen Null tendiert. Beispielsweise ist für n = 5000 die Differenz zwischen den Beziehungen 3091/5000 und 1909/3091 sind 0,006, was weniger als 0,1% des Durchschnitts dieser beiden Beziehungen entspricht.

Die Grafik in den beiden Abbildungen 9- (1,2) hat eine nicht zufällige Form der Variabilität, die einer Aufnahme auf einer „musikalischen Daube“ ähnelt. Wiederholte Sprünge nach oben und schrittweises Herunterfallen sind mit einer unregelmäßigen Periodizität sichtbar. Offensichtlich gibt es einen Grund für diese Art von Kurvenverhalten, und vielleicht ist dies für die Forschung von Interesse. Aus diesem Grund wurde das Diagramm zur detaillierteren Visualisierung in zwei Abbildungen dargestellt.

Ich habe nur einen Teil der Fragen betrachtet, die auf der Grundlage der Ergebnisse der Lösung des Problems "zur Verteilung von n-Königinnen" formuliert werden können. Ich hoffe, dass die erzielten Ergebnisse die Mechanismen der Bildung nicht deterministischer Prozesse und Veränderungen im Zustandsraum für das Verständnis transparenter machen. Vielleicht dient dies als Dreh- und Angelpunkt für die Formulierung neuer Aufgaben und für die weitere Entwicklung.

Fazit

• Wenn wir bei der Veröffentlichung zu einer Schlussfolgerung gelangt sind, stellt sich natürlich die Frage: "Was bedeutet die Problemlösung von One Billion Queens im Titel des Artikels?" Bei der Vorbereitung der Veröffentlichung für Habr dachte ich, dass eine Person, die zum Beispiel eine Mine hat, in der Diamanten abgebaut werden, ihren Freunden und Verwandten jeweils mindestens einen Diamanten geben sollte, sonst wäre es unfair. Deshalb möchte ich allen Mitgliedern der habr-Community ein Geschenk machen: Teilnehmern, Organisatoren, Besuchern. Wie der Name schon sagt, ist dies die Lösung für das Problem, eine Milliarde Königinnen auf einem Schachbrett mit einer Größe von einer Milliarde Milliarden zu verteilen.
  
  Natürlich ist dies kein facettierter Diamant, aber für echte Kenner der intellektuellen Kunst kann er wertvoller sein als "eine Art Diamant dort". Darüber hinaus gibt es weltweit viele verschiedene Diamanten, und diese Lösung ist bisher nur in einer Kopie erhältlich. Und unser Byte-Gott (*) sieht, dass ich das aufrichtig tue.
  Die resultierende Lösung ist ein eindimensionales Array mit einer Milliarde Zahlen, das im MatLab .mat-Format dargestellt wird und unter folgender Adresse verfügbar ist: One Billion Queens Problem Solution auf Google Drive
  -Das erste Element dieses Arrays kennzeichnet die Position der Königin in der ersten Zeile, das zweite Element - die Position in der zweiten Zeile usw. Dies ist nur eine Lösung von nBillion möglichen Lösungen. Und der Wert von nBillion ist so groß, dass er als enger Verwandter der Unendlichkeit angesehen werden kann.
  
• Es scheint mir, dass diese Lösung der Kategorie der virtuellen intellektuellen Werte zugeordnet werden kann. Wir können sagen, dass "dies etwas ist, in dem es etwas gibt". Sie können wirklich nicht „berührt“ werden, so dass sie im Bewusstsein nur auf der Ebene der Empfindungen wahrgenommen werden. Dort gibt es tatsächlich eine erstaunliche Ordnung und explizite und implizite Harmonie. Dies ist ein rein symbolisches Geschenk (wörtlich und im übertragenen Sinne), das an alle Mitglieder der Gemeinschaft gerichtet ist. Ich denke: " Du bist nicht wie alle anderen ."
  
  (Ich hoffe, jemand "nimmt das Geschenk mit nach Hause". Die Datei ist groß genug - 3,7 GB. Dies sind saubere, überprüfte Daten. Google Drive zeigt Warnungen an - behandeln Sie dies mit Verständnis.)
  
• Bevor ich diese Entscheidung traf, dachte ich über den individuell-kollektiven Charakter eines solchen Geschenks nach. Ist es möglich, dass man das Original und der Rest Kopien erhält? Aber die Lösung war einfach. Die üblichen "alltäglichen" Konzepte von "Original" und "Kopie" verlieren in diesem Fall ihre Bedeutung. Wir kopieren nicht, sondern erstellen ein anderes Original. Und die „Originale“ sind für alle gleich und gleichwertig.
  
• Ich denke, dass Sie in Begleitung von Verwandten höchstwahrscheinlich der einzige sein werden, der ein solches „intellektuelles Produkt“ als Geschenk erhalten hat. Es wird Spaß machen, wenn Sie Ihrer Schwiegermutter von einem solchen Geschenk erzählen: „Stellen Sie sich ein Schachbrett einer Mutter mit einer Größe von 50.000 x 50.000 km vor, auf dem 1 Milliarde Königinnen so verteilt sind, dass die eine die andere nicht aus nächster Nähe sieht ...“. Wer weiß, vielleicht wird der Schwiegersohn danach mehr geschätzt, da er ein so seltsames Geschenk erhält.
  

Ich wünsche allen Mitgliedern der Habr Community Gesundheit, Erfolg und Wohlbefinden. Möge das neue Jahr uns allen viel Glück bringen.

(*) - Da es sich um den Namen des Objekts handelt, sollte auch dessen Beschreibung angegeben werden.
Byte Gott bedeutet eine mehrdimensionale Einheit, bestehend aus Nullen und Einsen, die in jeder Hinsicht vernünftig und in alle Richtungen unendlich ist. Jede Folge von Nullen und Einsen in diesem Raum repräsentiert bestimmtes Wissen.

Referenzliste

[4] Max Bezzel, Vorschlag des 8-Königinnen-Problems ", Berliner Schachzeitung, Band
3 (1848), Seite 363. (Eingereicht unter dem Autorennamen \ Schachfreund ".)

[5] Franz Nauck, Briefwechseln mit allen fur alle ", Illustrirte Zeitung, Band
377 Nummer 15 (1850), Seite 182.

[6] Bell Jordan; Stevens Brett (2009). "Eine Übersicht über bekannte Ergebnisse und Forschungsbereiche für n-Königinnen." Diskrete Mathematik. 309 (1): 1–31

[7] Gent, Ian P.; Jefferson, Christopher; Nachtigall, Peter (August 2017). "Komplexität der n-Queens-Vervollständigung". Journal of Artificial Intelligence Research. AAAI Drücken Sie. 59: 815–848

[8] W. Kosters und alle, n-Queens - 342 Referenzen, (20. November 2018)

[9] NJA Sloane, die elektronisch veröffentlichte Online-Enzyklopädie ganzzahliger Sequenzen. 2016