Mathematische Modelle des Chaos

Einführung

Habr hat die Chaostheorie bereits in Artikeln [1,2,3] diskutiert. Die folgenden Aspekte der Chaostheorie werden in diesen Artikeln behandelt: verallgemeinertes Diagramm des Chua-Generators; Modellierung der Dynamik des Lorentz-Systems; Lorentz-, Rössler-, Rikitake- und Nose-Hoover-Attraktoren, programmiert durch logisch integrierte Schaltkreise.

Chaostheoretische Techniken werden jedoch auch verwendet, um biologische Systeme zu modellieren, die zweifellos eines der chaotischsten Systeme von allen sind, die man sich vorstellen kann. Dynamische Ausgleichssysteme wurden verwendet, um alles von Population und epidemischem Wachstum bis hin zu arrhythmischen Herzschlägen zu modellieren [4].

Tatsächlich kann fast jedes chaotische System modelliert werden - der Wertpapiermarkt generiert Kurven, die mit seltsamen Attraktoren leicht analysiert werden können. Der Vorgang, Tropfen aus einem undichten Wasserhahn fallen zu lassen, ist zufällig, wenn er mit dem bloßen Ohr analysiert wird. Wenn er jedoch als seltsamer Attraktor dargestellt wird, öffnet er sich eine übernatürliche Ordnung, die mit traditionellen Mitteln nicht zu erwarten war.

Der Zweck dieses Artikels ist es, die Theorie des Chaos am Beispiel der Erhöhung der Anzahl biologischer Populationen und der Verdoppelung des Zyklus in mechanischen Systemen mit grafischer Visualisierung mathematischer Modelle zu untersuchen, die auf einfachen intuitiven Programmen basieren, die in Python geschrieben wurden.

Der Artikel wurde zum Zweck des Unterrichts geschrieben, ermöglicht aber auch einem Leser ohne Programmiererfahrung, die oben genannten Programme zu verwenden, um die meisten neuen Bildungsprobleme zum Thema Modellierung von Chaosphänomenen unabhängig zu lösen.

Verdoppelung der Periode von Zyklen und Chaos am Beispiel des Wachstums der Anzahl biologischer Populationen

Betrachten wir zunächst die logistische Differentialgleichung, die einen begrenzten und keinen exponentiellen Anstieg der Anzahl biologischer Populationen modelliert:

$$$\ frac {dN} {dt} = aN-bN ^ {2}, (a, b> 0). (1)$

Diese Gleichung kann exotische und unerwartete Verhaltensmuster einiger Populationen vorhersagen. In der Tat, gemäß (1), für $$$t \ rightarrow + \ infty$ Die Bevölkerungsgröße nähert sich der Grenze gleich a / b .

Für die numerische Lösung der logistischen Differentiallösung können Sie den einfachsten Algorithmus verwenden, wobei der numerische Wert des Zeitschritts verwendet wird $$$t_ {n + 1} = t_ {n} + h$ Dann kann die Lösung (1) durch wiederholtes Anwenden der folgenden Beziehung erhalten werden:

$$$N_ {n + 1} = N_ {n} + (aN_n-bN {_ {n}} ^ {2}) h.$ (2)

Wir stellen Gleichung (2) in Form einer logistischen Gleichung in endlichen Differenzen dar:

$$$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$ . (3)

wobei: r = 1 + ah und s = bh .
Substitution in (3) $$$N_ {n} = \ frac {r} {s} x_ {n}$ Wir erhalten die iterative Formel:

$$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ , (4)

Wenn wir die durch Beziehung (3) gegebenen Werte berechnen, können wir eine Sequenz erzeugen $$$x_ {1}, x_ {2}, x_ {3}, .....$
Die Maximalwerte der Anzahl der Populationen, die die Umgebung zu bestimmten Zeiten unterstützt $$$t_ {1}, t_ {2}, t_ {3}.$ .

Wir gehen davon aus, dass es einen Grenzwert für Brüche gibt, die einen Teil der Bevölkerungsgröße ausdrücken:

$$$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$ , (5).

Wir werden untersuchen, wie es darauf ankommt $$$x _ {\ infty}$ aus dem Wachstumsparameter r in Gleichung (4). Zu diesem Zweck schreiben wir in Python ein Programm, das mit beginnt $$$x_ {1} = $ 0,$ berechnet die Ergebnisse bei mehreren hundert Iterationen ( n = 200 ) für r = 1,5; 2,0; 2,5 :


Das Ergebnis des Programms (um die Ausgabe der Ergebnisse zu reduzieren, werden die ersten drei und letzten vier Werte angegeben):

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000 

Eine Analyse des diskreten Modells zeigt, dass für r = 1,5; 2,0; 2,5 mit einer Zunahme der Anzahl von Iterationen der Wert ist $$$x_ {n}$ stabilisiert sich und wird fast gleich dem Grenzwert $$$x _ {\ infty}$ , die durch Beziehung (5) bestimmt wird. Darüber hinaus ist für die gegebenen Werte von r die Menge $$$x _ {\ infty}$ entsprechend gleich $$$x _ {\ infty} = 0,3333; 0,5000; $ 0,600$ .
Wir erhöhen r = 3,1; 3,25; 3,5 und die Anzahl der Iterationen n = 1008, dafür nehmen wir folgende Änderungen am Programm vor:


Das Ergebnis des Programms (um die Ausgabe der Ergebnisse zu reduzieren, werden die ersten vier und letzten acht Werte angegeben):

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269 

Wie aus den obigen Daten folgt, schwankt der Bruchteil der Bevölkerung zwischen zwei Fraktionen, wenn sich die Zeit ändert, anstatt sich in der Nähe einer einzelnen begrenzenden Population zu stabilisieren. Im Vergleich zu r = 3,1 verdoppelt sich die Zyklusdauer für r = 3,25 und für r = 3,5 viermal.


Das Ergebnis des Programms:



Aufgrund der Verdoppelung der Iterationsperiode $$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ wurde weithin bekannt. Wenn der Wert der Wachstumsrate r = 3,56 überschreitet, beschleunigt sich die Verdoppelung der Periode und es entsteht bereits am Punkt r = 3,57 ein extremes Chaos. Um den Beginn des Chaos anzuzeigen, verwenden wir das folgende Programm:


Das Ergebnis des Programms:

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397 

Wir werden ein Programm zur Visualisierung der Abhängigkeit des Iterationsverhaltens vom Wachstumsparameter r schreiben. Für jeden Wert von r im Intervall $$$a \ leqslant r \ leqslant b$ 1000 Iterationen werden durchgeführt, um Stabilität zu erreichen. Dann werden alle 250 Werte, die als Ergebnis von Iterationen erhalten wurden, entlang der vertikalen Achse aufgetragen und bilden Punkte ( r, x ):


Das Ergebnis in Form eines Diagramms:



Das resultierende Diagramm wird als „Verzweigungsdiagramm“ bezeichnet , mit dem Sie bestimmen können, ob ein bestimmter r- Wert einem Zyklus oder einem Chaos entspricht. Der einzige Wert der Bevölkerungsgröße wird zu bestimmt $$$r \ ca. 3$ dann ein Zyklus mit einer Periode von 2 bis $$$r \ ca. 3,4$ , dann ein Zyklus mit einer Periode von 4, dann ein Zyklus mit einer Periode von 8 und einer schnellen Annäherung an das Chaos.

Es ist zu beachten, dass die vertikalen Bereiche des nicht ausgefüllten Raums im Diagramm die Bereiche r = 3,6 und r = 3,7 sind , zwischen r = 3,7 und r = 3,8 , zwischen r = 3,8 und r = 3,9 wo die zyklische Ordnung aus dem vorherigen Chaos zurückkehrt.
Berücksichtigung des Auftretens eines Zyklus mit einem Periodenmultiplikator von 3 in der Region $$$3.8 \ leqslant r \ leqslant $ 3.$ Nehmen Sie Änderungen am vorherigen Programm vor:


Das Ergebnis des Programms:



Der Zyklus der Periode 3 erscheint in der Nähe des Punktes r = 3,83 und wird dann nacheinander in die Zyklen 6, 12, 24 unterteilt. Die Existenz eines Zyklus mit Periode 3 impliziert das Vorhandensein von Zyklen einer anderen endlichen Periode sowie von chaotischen Zyklen ohne jegliche Periode.

Das Verzweigungsdiagramm ermöglicht es Ihnen, die Entwicklung des Systems mit einer reibungslosen Änderung des Parameters zu verfolgen. Mit einem festen Wert des Parameters ermöglicht das Spinnendiagramm (Lamera-Diagramm) die Verfolgung der Punktbahnen.

Durch die Erstellung eines Spinnendiagramms können Sie verschiedene Effekte identifizieren, die im Verzweigungsdiagramm nicht sichtbar sind. Schreiben wir ein Programm:


Kameradiagramm:

Periodenverdopplung in mechanischen Systemen

Stellen Sie sich eine Differentialgleichung vor, die freie gedämpfte Schwingungen eines Materialpunkts einer bestimmten Masse auf einer nichtlinearen Feder modelliert, bei der die Dämpfung durch die Geschwindigkeit bestimmt wird.

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$ (6)

In Gleichung (6) repräsentiert der Term kx die Kraft einer linearen Feder, die auf einen Materialpunkt einer gegebenen Masse ausgeübt wird, und den Term $$$\ beta x ^ {3}$ repräsentiert die tatsächliche Nichtlinearität der Feder.

Wenn eine Kraft auf das System der freien Schwingungen (6) wirkt, wird die Verschiebung des Materialpunkts der Masse, auf die diese Kraft angewendet wird, durch die Duffing-Differentialgleichung für erzwungene Schwingungen beschrieben:

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$ (7)

Gleichung (7) für die meisten darin enthaltenen Parameter wird numerisch gelöst. Das mechanische System für das mathematische Modell gemäß Gleichung (7) ist in der Abbildung dargestellt:



Ein Merkmal des gegebenen Systems ist, dass anstelle einer Feder ein flexibles Metallgewinde verwendet wird, das in einer vertikalen Ebene schwingt, für die die Hakenkonstante k negativ ist. In diesem Schema sind die Punkte des stabilen Gleichgewichts (a) und (c) und der Punkt des instabilen Gleichgewichts (b).

Wenn ein Materialpunkt aus Position (b) verschoben wird, ist die auf ihn wirkende Kraft abstoßend. Wenn beispielsweise die durch das oszillierende Magnetfeld erzeugte periodische Kraft durch den Luftwiderstand teilweise gedämpft wird. Dann ist Gleichung (7) ein akzeptables mathematisches Modell für die horizontale Verschiebung x (t) eines Materialpunkts mit den folgenden Parameterbereichen $$$k <0, c> 0, \ beta> 0$ .

Um das Verhalten eines solchen nichtlinearen Systems zu untersuchen, nehmen wir $$$k = -1, m = c = \ beta = \ omega = 1$ dann nimmt die Differentialgleichung (7) die Form an:

$$$x ^ {''} + x ^ {'} - x + x ^ {3} = F_ {0} cos (t)$ , (8)

Wir schreiben ein Programm zur numerischen Integration von Gleichung (8) unter den Anfangsbedingungen $$$x (0) = 1, x ^ {'} (0) = 0$ im Gebiet $$$100 \ leqslant t \ leqslant 200$ und für jeden der folgenden Amplitudenwerte $$$F_ {0} = 0,6; 0,7; 0,75; 0,8$ Zeichnen Sie in jedem Fall die Lösungen für die Flugzeuge $$$x (t), x ^ {'} (t)$ und $$$t, x (t)$ ::


Diagramme als Ergebnis des Programms





Dieser Übergang von der Periodenverdopplung zum Chaos zeigt das allgemeine Verhalten eines nichtlinearen mechanischen Systems als Reaktion auf eine Änderung des entsprechenden physikalischen Parameters, zum Beispiel: $$$k, m, c, \ beta, \ omega, F_ {0}$ . Solche Phänomene treten in linearen mechanischen Systemen nicht auf.

Attraktor Lorenz

Die Substitution erzwungener Schwingungen (7) in die Duffing-Gleichung führt zu einem zweidimensionalen nichtlinearen System von Differentialgleichungen, das in der vorherigen Auflistung gezeigt wurde. Ein dreidimensionales nichtlineares System von Differentialgleichungen, wie es auf meteorologische Probleme angewendet wird, wurde von E.N. Lorenz:

$$$\ frac {dx} {dt} = - sx + sy,$
$$$\ frac {dy} {dt} = - xz + rx-y,$ (9)
$$$\ frac {dz} {dt} = xy-dz$

Die Lösung für System (9) lässt sich am besten in Projektion auf eine der drei Ebenen betrachten. Wir werden ein Programm zur numerischen Integration für die Parameter b = \ frac {8} {3}, s = 10, r = 28 und die Anfangsbedingungen x (0) = - 8, y (0) = 8, z (0) = 27 schreiben:


Das Ergebnis des Programms:



Wenn man das Bild in der Grafik über die Zeit betrachtet, kann angenommen werden, dass der Punkt P (x (t), y (t), z (t)) eine zufällige Anzahl von Schwingungen rechts oder links erzeugt. Für eine meteorologische Anwendung des Lorenz-Systems folgt nach einer zufälligen Anzahl klarer Tage eine zufällige Anzahl von Regentagen.

Stellen Sie sich ein Programm zur Abbildung des Lorentz-Attraktors in der xyz- Ebene für leicht unterschiedliche Anfangsbedingungen vor:


Die Ergebnisse des Programms sind in den folgenden Grafiken dargestellt:





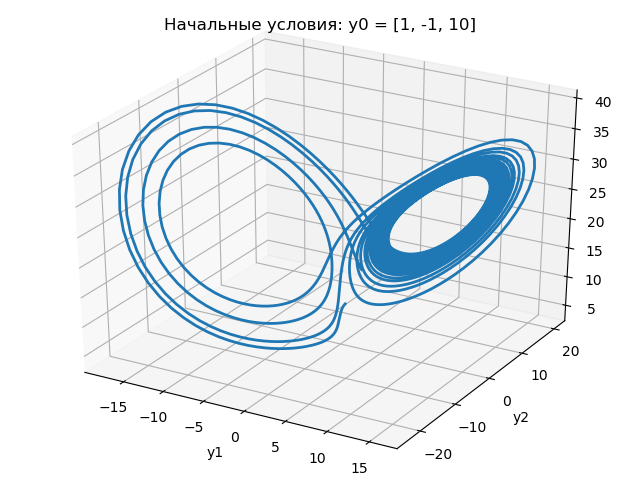
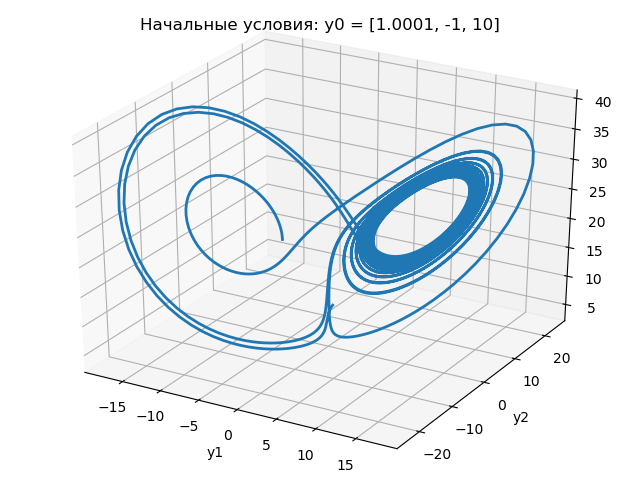
Aus den obigen Diagrammen folgt, dass eine Änderung des Anfangszustands von 1,0 auf 1.0001 die Art der Änderung des Lorentz-Attraktors dramatisch ändert.

Rossler-System

Dies ist ein sehr intensiv untersuchtes nichtlineares dreidimensionales System:
$$$\ frac {dx} {dt} = - y-z,$
$$$\ frac {dy} {dt} = x- \ alpha y,$ (10)
$$$\ frac {dz} {dt} = b + x (x-c).$

Wir werden ein Programm zur numerischen Integration von System (10) für die folgenden Parameter a = 0,39, b = 2, c = 4 unter den Anfangsbedingungen x (0) = 0, y (0) = 0, z (0) = 0 schreiben:


Das Ergebnis des Programms:



Im Flugzeug sieht Rosslers Band wie eine Schleife aus, aber im Weltraum stellt sich heraus, dass es wie ein Möbius-Band verdreht ist.

Schlussfolgerungen

Um die Phänomene des Chaos zu demonstrieren, werden einfache und intuitive Programme in einer Python-Programmiersprache auf hoher Ebene vorgestellt, die leicht auf neue Projekte zu diesem Thema aktualisiert werden können. Der Artikel hat einen pädagogischen und methodischen Schwerpunkt und kann im Lernprozess verwendet werden.

Referenzen

1. Ein bisschen über Chaos und wie man es schafft
2. Ein kritischer Blick auf den Lorenz-Attraktor
3. FPGA Chaos Generatoren
4. Differentialgleichungen und Randwertprobleme: Modellierung und Berechnung mit Mathematica, Maple und MATLAB. 3. Auflage .: Per. aus dem Englischen - M.: LLC “I.D. Williams, 2008. - 1104 p.: Ill. - Paral. tit. Englisch