Kürzlich wurde
Material in der Zeitschrift Quanta veröffentlicht, in dem der Autor über ein Phänomen sprach, das aus Sicht unerfahrener Leser überraschend war und von Mathematikern bewiesen wurde. Sein Wesen ist, dass fast alle Polynome eines bestimmten Typs irreduzibel sind, das heißt, sie können nicht zerlegt werden. Dieser Beweis wird in vielen Bereichen der reinen Mathematik angewendet. Aber auch dies ist eine gute Nachricht für eine der Säulen des modernen Lebens - die digitale Verschlüsselung.
Zur zuverlässigen Speicherung digitaler Informationen wird häufig die Verschlüsselung mit dem RSA-Algorithmus verwendet. Dies ist eine aufgepumpte Version des Schemas, die selbst ein Siebtklässler entwickeln kann, um Nachrichten mit Freunden auszutauschen: Jedem Buchstaben wird eine Nummer zugewiesen, die mit einem geheimen, im Voraus vereinbarten Schlüssel multipliziert wird. Um eine Nachricht zu entschlüsseln, teilen Sie sie einfach in einen geheimen Schlüssel.
Die RSA-Verschlüsselung funktioniert auf ähnliche Weise. Wir geben eine sehr vereinfachte Erklärung. Der Benutzer wartet mit einer Nachricht auf und führt bestimmte mathematische Operationen aus, einschließlich des Multiplizierens mit einer sehr großen Zahl (mehrere hundert Stellen lang). Die einzige Möglichkeit, die Nachricht zu entschlüsseln, besteht darin, einfache Faktoren für das Ergebnis * zu finden.
* *Die Primfaktoren einer Zahl sind die Primzahlen, die multipliziert werden müssen, um diese Zahl zu erhalten. Für die Zahl 12 ist es also 2 * 2 * 3 und für die Zahl 495 3, 3, 5 und 11.
Die Sicherheit der RSA-Verschlüsselung basiert auf der Tatsache, dass die Mathematik keine schnellen Möglichkeiten kennt, Primfaktoren mit sehr großen Zahlen zu finden. Und wenn die verschlüsselte Nachricht nicht für Sie bestimmt war und Sie keinen Schlüssel zum Entschlüsseln haben, kann der Versuch, diesen Schlüssel zu finden, gut tausend Jahre dauern. Darüber hinaus gilt dies auch für die modernsten Computer, mit deren Hilfe die richtigen einfachen Faktoren immer noch nicht ausgewählt werden können.
Es gibt jedoch eine Problemumgehung.
Jede Zahl kann als eindeutige algebraische Gleichung dargestellt werden. Und im Gegensatz zur Suche nach Primfaktoren einer Zahl ist die Suche nach Primfaktoren eines Polynoms viel einfacher. Und sobald das Polynom in solche Primfaktoren zerlegt ist, können diese Informationen verwendet werden, um nach Primfaktoren der ursprünglichen Zahl zu suchen.
So funktioniert es
Erster Schritt: Wählen Sie eine beliebige Zahl, deren Primfaktoren Sie herausfinden müssen. Nehmen Sie der Einfachheit halber die Nummer 15.
Schritt zwei: 15 übersetzt in binär:
1111.
Schritt drei: Dieser binäre Ausdruck wird zu einem Polynom, indem alle binären Zahlen in Koeffizienten des Polynoms übersetzt werden:
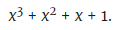
(Hinweis: Dieses Polynom ist 15, wenn x = 2. Nummer 2 ist die Basis des Binärsystems.)
Vierter Schritt: Das Polynom wird faktorisiert:
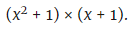Fünfter Schritt: x = 2 wird in jeden dieser Faktoren eingesetzt:
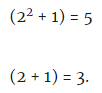Schlussfolgerung: 5 und 3 sind Primfaktoren von 15.
Ja, dies ist eine übermäßig komplizierte Methode, um einfache Faktoren mit einer kleinen Zahl wie 15 zu finden, die im Kopf leicht herauszufinden sind. Wenn es jedoch um große Zahlen geht, die aus Hunderten von Zahlen bestehen, bietet diese Polynommethode einen erstaunlichen Vorteil. Für die Zerlegung von Primzahlen existieren keine schnellen Algorithmen. Es gibt jedoch solche Algorithmen zum Zerlegen großer Polynome. Sobald Sie es also schaffen, eine große Zahl in ein großes Polynom umzuwandeln, können Sie sehr nahe daran sein, einfache Faktoren der Zahl zu finden.
Bedeutet dies, dass die RSA-Verschlüsselung gefährdet ist? Nicht wirklich. Und ein neues, kürzlich bewiesenes Muster in Bezug auf Polynome ist genau damit verbunden.
Die Mathematiker
Emmanuel Brulya und
Peter Varju von der Universität Cambridge haben bewiesen, dass mit zunehmender
Länge von Polynomen mit den Koeffizienten 0 und 1 die Wahrscheinlichkeit, dass sie überhaupt erweitert werden können, geringer wird. Und wenn das Polynom nicht zerlegt werden kann, kann es nicht verwendet werden, um nach einfachen Faktoren der Zahl zu suchen, die berechnet werden muss.
Die Beweise von Brull und Varju deuten tatsächlich darauf hin, dass eine Problemumgehung zum Knacken der RSA-Verschlüsselung nirgendwo hin führt. Die in RSA verwendeten sehr großen Zahlen entsprechen sehr langen Polynomen. Wissenschaftler aus Cambridge argumentieren, dass es fast unmöglich ist, Polynome dieser Länge zu finden, die zerlegt werden können. Sowohl Kryptographen als auch Mathematiker haben lange vermutet, dass dies so ist. Wenn die weltweite Cybersicherheit jedoch von der Unmöglichkeit abhängt, eine mathematische Technik zu verwenden, ist es immer gut, den Beweis zu haben, dass diese Technik nicht wirklich funktioniert.
