Biquaternionen

Wenn Sie diesen Artikel geöffnet haben, haben Sie wahrscheinlich bereits von Quaternionen gehört und sie möglicherweise sogar in Ihren Entwürfen verwendet. Aber es ist Zeit, auf ein höheres Niveau aufzusteigen - zu den Biquaternionen.

Dieser Artikel enthält grundlegende Konzepte zu Biquaternionen und Operationen mit ihnen. Zum besseren Verständnis der Arbeit mit Biquaternionen wird ein klares Beispiel in Javascript unter Verwendung von Canvas gezeigt.

Biquaternion

Das Biquaternion ist eine hyperkomplexe Zahl mit einer Dimension von 8. In englischsprachigen Artikeln und in der Literatur werden sie als "duales Quaternion" bezeichnet, und in der russischsprachigen Literatur gibt es auch die Namen "duales Quaternion" oder "komplexes Quaternion".

Der Hauptunterschied zu Quaternionen besteht darin, dass die Quaternion die Ausrichtung des Objekts im Raum beschreibt und die Biquaternion auch die Position des Objekts im Raum beschreibt.

Biquaternion kann als zwei Quaternionen dargestellt werden:

$$

$$\ widetilde {\ textbf {q}} = \ begin {bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix},$$

$$$\ textbf {q} _1$ - der Realteil bestimmt die Ausrichtung des Objekts im Raum;
$$$\ textbf {q} _2$ - Der Doppelteil bestimmt die Position des Objekts im Raum.

Das Biquaternion wird auch als komplexes Quaternion bezeichnet. In diesem Fall wird es als Quaternion dargestellt, wobei jede Komponente eine doppelte Zahl ist (nicht zu verwechseln mit dem Komplex). Doppelte Nummer $$$A = a_1 + \ epsilon a_2$ wo $$$a_1$ und $$$a_2$ Sind reelle Zahlen und $$$\ epsilon$ - Clifford-Symbol (Komplexität), das die Eigenschaft besitzt $$$\ epsilon ^ 2 = 0$ . Wir werden uns nicht mit Mathematik befassen, da wir uns mehr für den angewandten Teil interessieren. Daher werden wir die Biquaternion weiter als zwei Quaternionen betrachten.

Geometrische Interpretation der Biquaternion

In Analogie zur Quaternion, mit der Sie die Ausrichtung des Objekts festlegen können, kann die Biquaternion auch die Position festlegen. Das heißt, Die Biquaternion legt zwei Werte gleichzeitig fest - die Position und Ausrichtung des Objekts im Raum. Wenn wir sie in der Dynamik betrachten, definiert das Biquaternion zwei Größen - die lineare Bewegungsgeschwindigkeit und die Winkeldrehgeschwindigkeit des Objekts. Die folgende Abbildung zeigt die geometrische Bedeutung der Biquaternion.



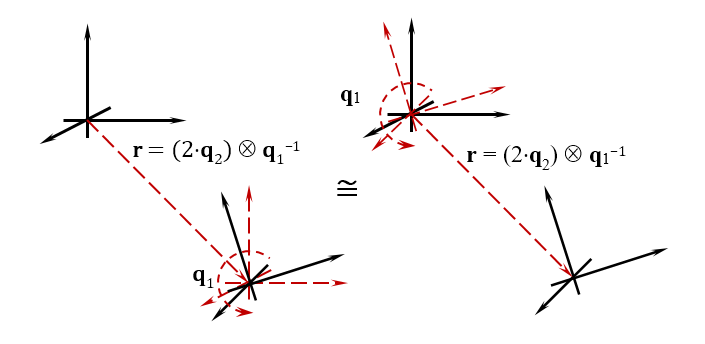
Spieleentwickler wissen, dass zur Bestimmung der Position und Ausrichtung eines Objekts im Spielraum Rotationsmatrizen und Verschiebungsmatrizen verwendet werden. Abhängig von der Reihenfolge, in der Sie sie anwenden, ist das Ergebnis der endgültigen Position des Objekts unterschiedlich. Für diejenigen, die es gewohnt sind, die Bewegung in separate Operationen zu unterteilen, akzeptieren Sie die Regel für die Arbeit mit Biquaternionen: Zuerst bewegen wir das Objekt, dann drehen wir es. Tatsächlich beschreiben Sie diese beiden Bewegungen mit einer einzigen Zahl, wenn auch mit einem komplexen Hyperkomplex.

Skalareigenschaften

Berücksichtigen Sie die wichtigsten Skalareigenschaften. Hierbei ist darauf zu achten, dass sie keine gewöhnlichen reellen Zahlen zurückgeben, sondern doppelte.

1. Die Norm der Biquaternion

$$

$$\ | \ widetilde {\ textbf {q}} \ | = \ | \ textbf {q} _1 \ | + \ epsilon (q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2)$$

2. Biquaternion-Modul

$$

$$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1 |}$$

Grundlegende Operationen

Betrachten Sie die grundlegenden Operationen der Arbeit mit Biquaternionen. Wie Sie sehen können, sind sie ähnlichen Operationen mit Quaternionen sehr ähnlich.

1. Biquaternion-Paarung

$$

$$\ widetilde {\ textbf {q}} ^ * = \ begin {bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$$

2. Addition und Subtraktion von Biquaternionen

$$

$$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ pm \ textbf {p} _2 \ end {bmatrix}$$

Das Addieren und Subtrahieren von Biquaternionen ist kommutativ (Begriffe können ausgetauscht werden).

3. Multiplikation der reellen Zahl durch Biquaternion

$$

$$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ begin {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$$

4. Biquaternion Multiplikation

$$

$$\ widetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ otimes \ textbf {p} _1 \\ \ textbf {q} _1 \ otimes \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$$

Die Biquaternion-Multiplikation ist nicht kommutativ (bei einer Änderung der Reihenfolge der Faktoren ist das Ergebnis der Biquaternion-Multiplikation unterschiedlich).

Diese Operation ist eine der Hauptoperationen bei der Arbeit mit Biquaternionen und hat eine physikalische Bedeutung, nämlich das Ergebnis der Biquaternionenmultiplikation ist die Operation des Addierens der Rotationen und linearen Bewegungen von zwei Biquaternionen.

5. Biquaternion umkehren

$$

$$\ widetilde {\ textbf {q}} ^ {- 1} = \ frac {\ widetilde {\ textbf {q}} ^ *} {\ | \ widetilde {\ textbf {q}} \ |}$$

Bestimmung der Biquaternion durch Orientierungswinkel und Positionsvektor

Zunächst definieren wir die Koordinatensysteme, in denen wir die Ausrichtung und Position des Objekts im Raum berücksichtigen. Dies muss durchgeführt werden, um den Realteil des Biquaternions (Orientierungsquaternion) anzugeben, dessen Rotationssequenz das resultierende Quaternion aus den Orientierungswinkeln beeinflusst. Hier werden wir von Flugzeugwinkeln geführt - Gieren $$$\ psi$ Tonhöhe $$$\ vartheta$ und rollen $$$\ gamma$ .

Definieren Sie das Basiskoordinatensystem. Stellen Sie sich vor, Sie stehen auf der Erdoberfläche und schauen in Richtung Norden.

Punkt O _o - der Ursprung des Koordinatensystems am Ursprungspunkt des Objekts.
Die Achse O _o Y _g - ist vertikal nach oben gerichtet und der Richtung des Schwerkraftvektors entgegengesetzt.
Die Achse O _o X _g - ist entlang der Tangente des lokalen Meridians nach Norden gerichtet.
Achse O _o Z _g - ergänzt das System nach rechts und ist nach rechts in Richtung Osten gerichtet.

Das zweite Koordinatensystem ist verbunden. Stellen Sie sich zum Beispiel ein Flugzeug oder ein anderes Objekt vor.
Punkt O - Der Ursprung des Koordinatensystems liegt in der Regel am Punkt des Massenschwerpunkts des Objekts.
OY- Achse - vertikal nach oben gerichtet und senkrecht zur horizontalen Ebene des Objekts.
Achse OX - nach vorne zum vorderen Punkt des Objekts gerichtet.
OZ- Achse - ergänzt das System auf der rechten Seite.

Die Position des Objekts im Raum wird durch den Radiusvektor des Ursprungs (Punkt O ) des zugehörigen Koordinatensystems relativ zum festen Basiskoordinatensystem bestimmt. Die Ausrichtung des zugehörigen Koordinatensystems relativ zur Basis wird durch drei aufeinanderfolgende Einschaltungen bestimmt:

Gierwinkel $$$\ psi$ - Drehung um die Achse OY ,
Nickwinkel $$$\ vartheta$ - Drehung um die Achse OZ ,
Rollwinkel $$$\ gamma$ - Drehung um die Achse OX .

Für die anfängliche Bestimmung der Biquaternion müssen Sie den Real- und den Doppelteil der Biquaternion angeben. Die Ausrichtung und Position des Objekts wird unter Verwendung von Ausrichtungswinkeln relativ zu einem bestimmten Basiskoordinatensystem festgelegt $$$\ psi, \ vartheta, \ gamma$ und Positionsvektor des Massenschwerpunkts $$$r = (r_x, r_y, r_z) ^ T$ .

Der eigentliche Teil $$$\ textbf {q} _1$ kann mit der Formel eingestellt werden:

$$

$$\ textbf {q} _1 = \ begin {bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ cos \ frac { \ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \ end {bmatrix}$$

Bitte beachten Sie, dass bei einer anderen Rotationssequenz auch die Ausdrücke unterschiedlich sind.

Doppelteil $$$\ textbf {q} _2$ definiert durch den Ausdruck:

$$

$$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$$

Berechnung der Orientierungswinkel und des Positionsvektors aus der Biquaternion. Inverse Transformation

Die Orientierungswinkel können aus dem Realteil der Biquaternion berechnet werden $$$\ textbf {q} _1$ ::

$$

$$\ psi = \ arctan {\ frac {2 (q_0 q_2 - q_1 q_3)} {q_0 ^ 2 + q_1 ^ 2 - q_2 ^ 2 - q_3 ^ 2}}$$

$$

$$\ vartheta = \ arcsin {(2 (q_1 q_2 + q_0 q_3))}$$

$$

$$\ gamma = \ arctan {\ frac {2 (q_0 q_1 - q_2 q_3)} {q_0 ^ 2 - q_1 ^ 2 + q_2 ^ 2 - q_3 ^ 2}}$$

Die Position des Objekts wird durch den Ausdruck bestimmt:

$$

$$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {- 1}$$

Das Ergebnis ist ein Vektor in Quaternionsform $$$\ textbf {r} = (0, r_x, r_y, r_z) ^ T$

Drehen und bewegen Sie die Vektorbiquaternion

Eine der großen Eigenschaften von Biquaternionen ist die Drehung und Bewegung eines Vektors von einem Koordinatensystem zum anderen. Sei O _o X _g Y _g Z _g ein festes Basiskoordinatensystem und OXYZ das verbundene Koordinatensystem des Objekts. Dann kann die Ausrichtung und Position des Objekts relativ zum Basiskoordinatensystem durch die Biquaternion festgelegt werden $$$\ widetilde {\ textbf {q}}$ . Wenn ein Vektor angegeben ist $$$\ textbf {r}$ In einem verbundenen Koordinatensystem können Sie dann einen Vektor erhalten $$$\ textbf {r} _0$ im Basiskoordinatensystem mit der Formel:

$$

$$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {- 1}$$

und zurück:

$$

$$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {- 1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}}$$

wo $$$\ textbf {r}$ Ist ein Vektor in Biquaternionsform, $$$\ textbf {r} = (1, 0, 0, 0, 0, r_x, r_y, r_z)$

Biquaternion JavaScript Library

Alle oben genannten Operationen mit Biquaternionen sind in der Javascript-Bibliothek implementiert, abhängig von Ihren Aufgaben, die in anderen Programmiersprachen implementiert werden können. Die Hauptfunktionen der Arbeit mit Biquaternionen:

Funktion	Beschreibung
DualQuaternion.dq	Biquaternion Körper als Array von 8 Zahlen
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)	Ein Konstruktor, der eine Biquaternion definiert, indem er alle acht Zahlen angibt
DualQuaternion.fromEulerVector(psi, theta, gamma, v)	Holen Sie sich die Biquaternion, indem Sie die Ausrichtung des Objekts mit Euler-Winkeln und dem Positionsvektor des Objekts einstellen
DualQuaternion.getEulerVector()	Holen Sie sich Euler-Winkel und Positionsvektor von Biquaternion
DualQuaternion.getVector()	Holen Sie sich den Positionsvektor von Biquaternion
DualQuaternion.getReal()	Holen Sie sich den Realteil der Biquaternion (bestimmt die Ausrichtung des Objekts im Raum)
DualQuaternion.getDual()	Holen Sie sich den doppelten Teil der Biquaternion (bestimmt die Position des Objekts im Raum)
DualQuaternion.norm()	Holen Sie sich die Biquaternion-Norm als doppelte Zahl
DualQuaternion.mod()	Holen Sie sich das Biquaternion-Modul als doppelte Nummer
DualQuaternion.conjugate()	Holen Sie sich die konjugierte Biquaternion
DualQuaternion.inverse()	Holen Sie sich Reverse Biquaternion
DualQuaternion.mul(DQ2)	Biquaternion Multiplikation
DualQuaternion.toString()	Konvertieren Sie die Biquaternion in eine Zeichenfolge, um sie beispielsweise an die Debug-Konsole auszugeben

Ein Beispiel für die Arbeit mit Biquaternionen

Betrachten Sie ein kleines Spiel, um die Grundlagen der Verwendung von Biquaternionen als Beispiel besser zu verstehen. Der rechteckige Bereich wird festgelegt - die Karte. Ein Schiff, das auf einer Karte mit einer auf der Karte montierten Rotationskanone schwimmt. Hierbei ist zu berücksichtigen, dass für das Schiff das Grundkoordinatensystem das Koordinatensystem der Karte und für die Waffe das Grundkoordinatensystem das Schiff ist. Alle Objekte werden im Kartenkoordinatensystem gezeichnet. Hier ist es interessant zu sehen, wie Sie mithilfe der Biquaternion-Multiplikationseigenschaft vom Kanonenkoordinatensystem zum Kartenkoordinatensystem wechseln können. Die Bewegung des Schiffes wird mit den Tasten W, A, S, D gesteuert. Die Richtung der Waffe wird mit dem Mauszeiger eingestellt.



Das Schiff und die Waffe werden in zwei Klassen beschrieben: Ship und Gun . Im Konstruktor der Schiffsklasse werden seine Form in Form von Biquaternionspunkten, die anfängliche Ausrichtung und Position auf der Karte in Form this.dq_pos Biquaternion.dq_pos this.dq_pos .

Biquaternion-Inkremente werden auch für die Schiffskontrolle angegeben. Beim Hin- und Herbewegen (Tasten W, S) ändert sich nur der doppelte Teil des Biquaternions, und beim Steuern von rechts nach links (Tasten A, D) ändern sich der reale und der doppelte Teil des Biquaternions, wodurch der Drehwinkel festgelegt wird.

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); //   this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); //      this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; }; 

In der Klasse selbst gibt es nur eine Funktion zum Rendern des Ship.draw() . Achten Sie auf die Anwendung der Biquaternion-Operation, bei der jeder Punkt des Schiffes mit der Biquaternion der aktuellen Position und Ausrichtung des Schiffes multipliziert wird.

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** *   */ 'draw': function() { //         v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } }; 

Im Konstruktor der Waffenklasse wird seine Form in Form von Biquaternionspunkten angegeben. Die Waffe wird als Linie angezeigt. Die anfängliche Ausrichtung und Position auf dem Schiff wird durch die Biquaternion this.dq_pos . Außerdem wird die Bindung an das Schiff festgelegt, auf dem es installiert ist. Die Waffe auf dem Schiff kann sich nur drehen, so dass Biquaternion-Inkremente bei der Steuerung der Waffe nur den Realteil der Biquaternion ändern, der den Drehwinkel festlegt. In diesem Beispiel wird das Gerät vom Mauszeiger geführt, sodass die Drehung der Pistole sofort erfolgt.

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; //     this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); //   this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); //     this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; }; 

In der Ship.draw() auch nur eine Funktion des Renderings Ship.draw() implementiert. Die Waffe wird als Linie angezeigt, die durch zwei Punkte this.dq_backward und this.dq_forward . Um die Koordinaten der Punkte der Waffe zu bestimmen, wird die Operation der Biquaternion-Multiplikation verwendet.

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** *   */ 'draw': function() { //     v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } }; 

Die Verarbeitung der Schiffs- und Waffensteuerung wird durch Ereignisse implementiert. Vier Variablen leftPressed, upPressed, rightPressed, downPressed , die in der Hauptprogrammschleife verarbeitet werden, sind für das Drücken und Loslassen der Schiffssteuertasten verantwortlich.

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); //     function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } //  S } //     function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } //  S } 

Eine der interessantesten Funktionen im Hinblick auf die Verwendung von Biquaternion-Operationen besteht darin, die Schiffskanone in Richtung des Mauszeigers zu steuern. Zunächst werden die Koordinaten des Mauszeigers in der Biquaternion dq_mouse_pos . Dann wird die Biquaternion der Position der Maus relativ zum Schiff unter Verwendung der Biquaternion-Multiplikation berechnet. Die Biquaternion des Schiffes wird der Maus entnommen. Biquaternion dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(Hinweis: Sequentielle Biquaternion-Multiplikationsoperationen werden von rechts nach links gelesen). Und schließlich wird der Winkel zwischen den Vektoren des Werkzeugs und der Maus bestimmt. Dem Startpunkt der Waffe gun_1.dq_backward der empfangene Wert zugewiesen.

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; //           if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { //    dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); //      //  .       //     // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); //       q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } } 

Im Hauptteil des Programms werden Objekte des Schiffs und der Kanonen ship_1 und gun_1 , Debugging-Informationen angezeigt und die Schiffssteuerungsverarbeitung durchgeführt.

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); //   if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw(); 

Der Link zum Archiv enthält den vollständigen Code der Bibliotheken für die Arbeit mit Quaternionen und Biquaternionen, das Programmskript selbst und die Datei index.html, die lokal im Browser geöffnet werden kann, um das obige Beispiel auszuführen.

Ein Beispiel für die Arbeit mit Biquaternionen

Fazit

Möglicherweise haben Sie eine Frage: Warum sollten Sie einen so komplexen mathematischen Apparat verwenden, wenn Sie mit Standardwerkzeugen zum Bewegen und Drehen von Objekten auskommen können? Einer der Hauptvorteile besteht darin, dass die Biquaternionsform des Schreibens rechnerisch effizienter ist, da alle Operationen mit Biquaternionen nach dem Erweitern der Ausdrücke linear sind. Dieses Video, Geometrisches Skinning mit ungefährer Mischung aus zwei Quaternionen, zeigt, wie viel effizienter Biquaternionsberechnungen sind als andere Methoden.

Ich habe hauptsächlich Informationen über die Verwendung von Biquaternionen aus englischen Quellen entnommen.
Aus der heimischen Literatur kann ich zwei Bücher empfehlen:

1. Chelnokov Yuri Nikolaevich. Quaternion- und Biquaternion-Modelle und Methoden der Festkörpermechanik und ihre Anwendungen. Geometrie und Bewegungskinematik. - monumentale theoretische Arbeit.
2. Gordeev Vadim Nikolaevich. Quaternionen und Biquaternionen mit Anwendungen in Geometrie und Mechanik. - Es ist in einer verständlicheren Sprache verfasst und zeigt Anwendungen bei der Gestaltung gekrümmter räumlicher Strukturen.