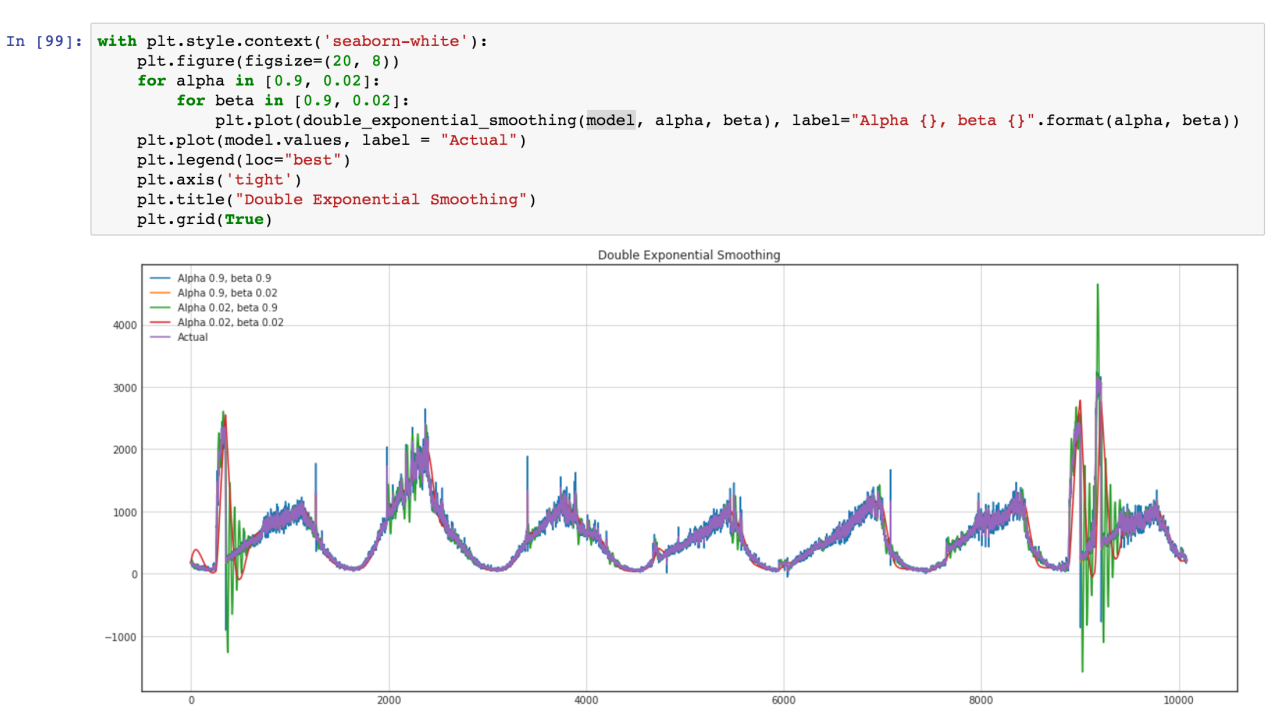
Dies ist ein kurzer Artikel über das Verständnis von Zeitreihen und den Hauptmerkmalen dahinter.
Problemm Aussage
Wir haben Zeitreihendaten mit täglicher und wöchentlicher Regelmäßigkeit. Wir möchten herausfinden, wie diese Daten optimal modelliert werden können.

Zeitreihen analysieren
Eines der wichtigen Merkmale von Zeitreihen ist die Stationarität.
In Mathematik und Statistik ist ein stationärer Prozess (auch bekannt als strikter (ly) stationärer Prozess oder starker (ly) stationärer Prozess) ein stochastischer Prozess, dessen gemeinsame Wahrscheinlichkeitsverteilung sich bei zeitlicher Verschiebung nicht ändert.
Folglich ändern sich auch Parameter wie Mittelwert und Varianz, falls vorhanden, nicht im Laufe der Zeit. Da Stationarität eine Annahme ist, die vielen statistischen Verfahren zugrunde liegt, die bei der Zeitreihenanalyse verwendet werden, werden instationäre Daten häufig in stationäre Daten umgewandelt.
Die häufigste Ursache für die Verletzung der Stationarität sind Trends im Mittelwert, die entweder auf das Vorhandensein einer Einheitswurzel oder auf einen deterministischen Trend zurückzuführen sind. Im ersteren Fall einer Einheitswurzel haben stochastische Schocks dauerhafte Auswirkungen und der Prozess ist nicht mittelwertig. Im letzteren Fall eines deterministischen Trends wird der Prozess als stationärer Trendprozess bezeichnet, und stochastische Schocks haben nur vorübergehende Effekte, die den Mittelwert zurücksetzen (d. H. Der Mittelwert kehrt zu seinem langfristigen Durchschnitt zurück, der sich im Laufe der Zeit deterministisch ändert der Trend).
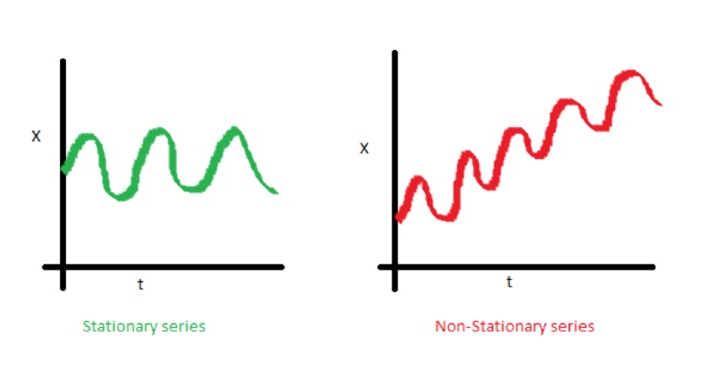
Beispiele für stationäre und instationäre Prozesse
Trendlinie
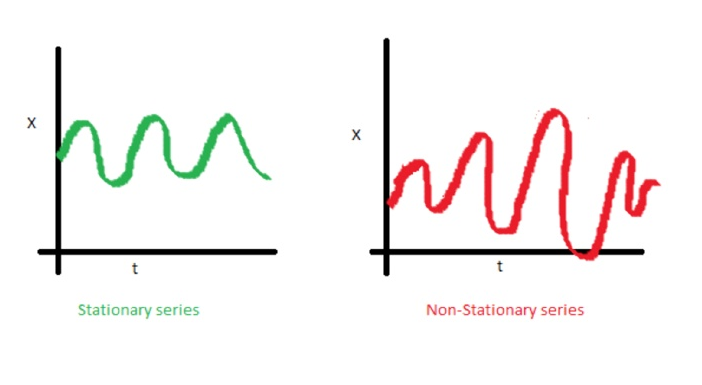
Dispersion
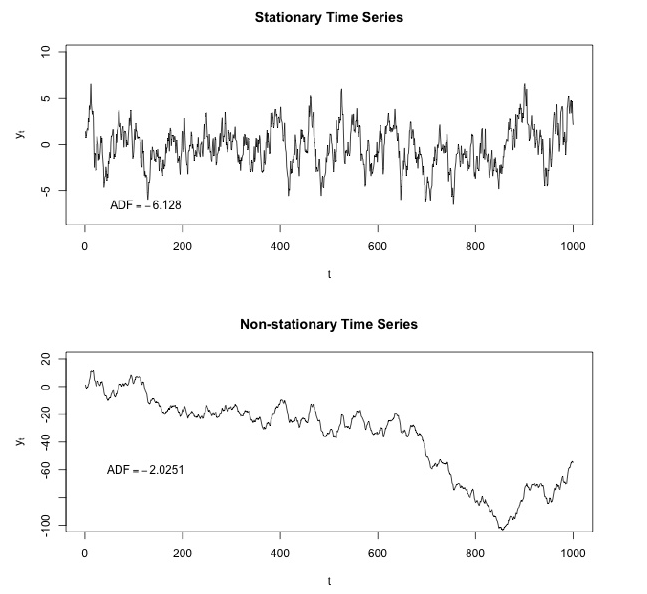
Weißes Rauschen ist ein stochastischer stationärer Prozess, der mit zwei Parametern beschrieben werden kann: Mittelwert und Dispersion (Varianz). In diskreter Zeit ist weißes Rauschen ein diskretes Signal, dessen Abtastwerte als eine Folge von seriell nicht korrelierten Zufallsvariablen mit einem Mittelwert von Null und einer endlichen Varianz betrachtet werden.
Wenn wir auf die Achse y projizieren, können wir eine Normalverteilung sehen. Weißes Rauschen ist ein zeitlicher Gauß-Prozess.
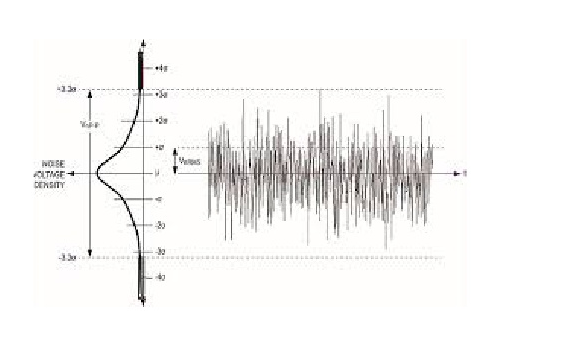
In der Wahrscheinlichkeitstheorie ist die Normalverteilung (oder Gaußsche Verteilung) eine sehr häufige kontinuierliche Wahrscheinlichkeitsverteilung. Normalverteilungen sind in der Statistik wichtig und werden in den Natur- und Sozialwissenschaften häufig verwendet, um reelle Zufallsvariablen darzustellen, deren Verteilungen nicht bekannt sind. Die Normalverteilung ist aufgrund des zentralen Grenzwertsatzes nützlich. In seiner allgemeinsten Form heißt es unter bestimmten Bedingungen (einschließlich endlicher Varianz), dass Durchschnittswerte von Stichproben von Beobachtungen von Zufallsvariablen, die unabhängig von unabhängigen Verteilungen gezogen wurden, in der Verteilung zur Normalen konvergieren, dh normal verteilt werden, wenn die Anzahl der Beobachtungen ist ausreichend groß. Physikalische Größen, von denen erwartet wird, dass sie die Summe vieler unabhängiger Prozesse sind (z. B. Messfehler), weisen häufig nahezu normale Verteilungen auf. Darüber hinaus können viele Ergebnisse und Methoden (wie die Ausbreitung der Unsicherheit und die Anpassung der Parameter der kleinsten Quadrate) in expliziter Form analytisch abgeleitet werden, wenn die relevanten Variablen normal verteilt sind.
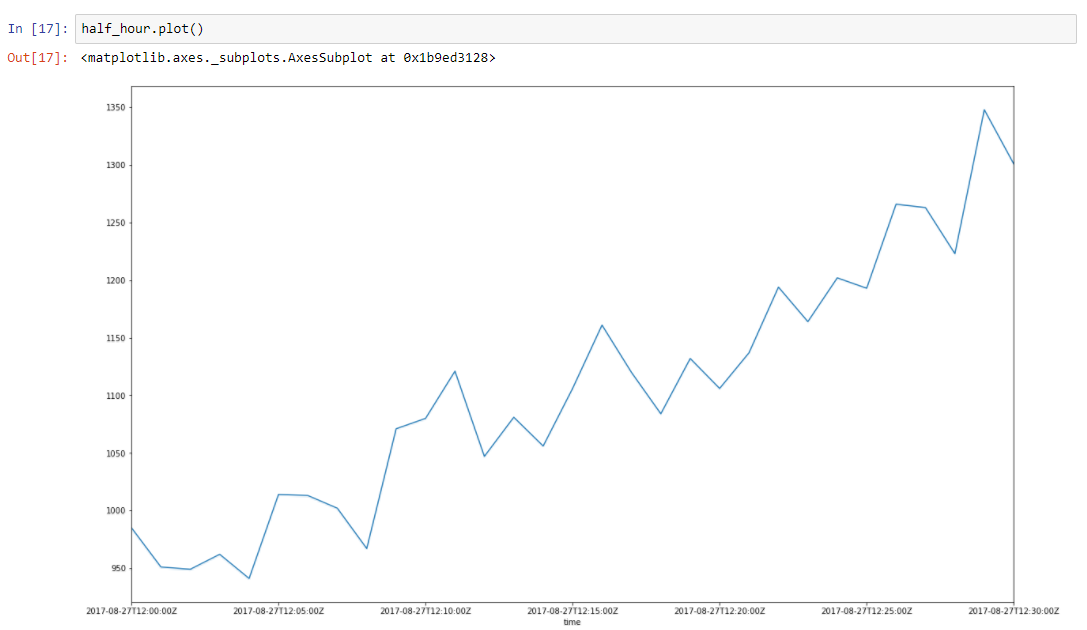
Angenommen, unsere Daten weisen einen Trend auf. Spitzen in der Umgebung sind auf viele zufällige Faktoren zurückzuführen, die sich auf unsere Daten auswirken. Beispielsweise wird die Anzahl der zugestellten Anfragen mit diesem Ansatz sehr gut beschrieben. Speicherbereinigung, Cache-Fehler, Paging nach Betriebssystem, viele Dinge beeinflussen die bestimmte Zeit der zugestellten Antwort. Nehmen wir eine halbe Stunde Zeit von unseren Daten, von 2017–08–27 12:00 bis 12:30 Uhr. Wir können sehen, dass diese Daten einen Trend und einige Schwingungen aufweisen
Erstellen wir eine Regressionslinie zum Definieren der Steigung dieser Trendlinie.
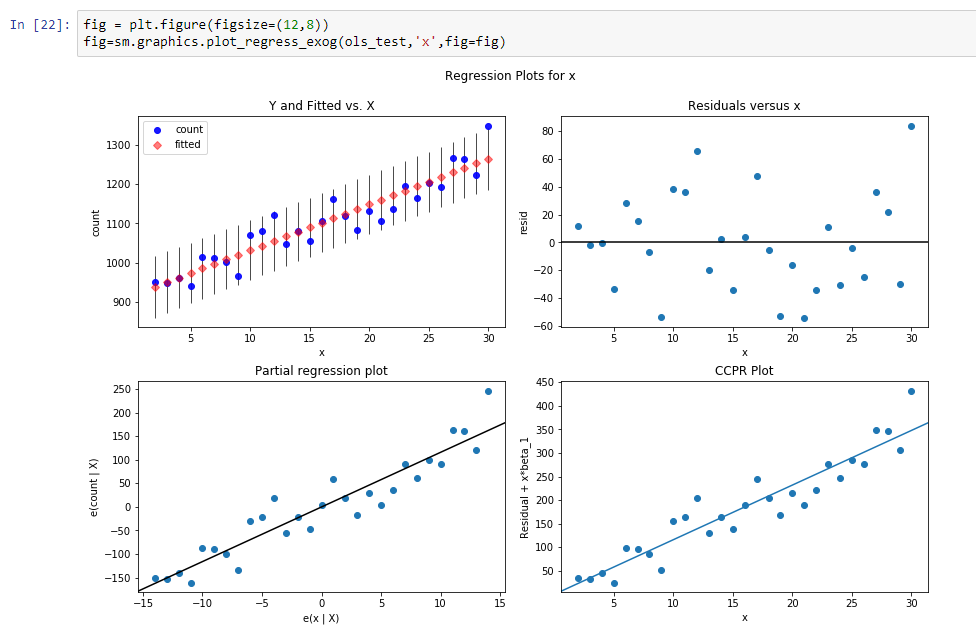
Ergebnisse dieser Regression sind:
const 916.269951dy / dx 11,599507Ergebnisse bedeuten, dass const ein Level für diese Trendlinie ist und dy / dx eine Steigungslinie ist, die definiert, wie schnell das Level mit der Zeit wächst.
Tatsächlich reduzieren wir die Dimension der Daten von 31 Parametern auf 2 Parameter. Wenn wir unsere Regressionsfunktionswerte von unseren Anfangsdaten abziehen, sehen wir einen Prozess, der wie ein stationärer stochastischer Prozess aussieht.
Nach der Subtraktion können wir also sehen, dass der Trend verschwunden ist und wir können davon ausgehen, dass der Prozess in diesem Bereich stochastisch ist. Aber wie können wir sicher sein.

Lassen Sie uns
Dickey - Fuller Test machen .
Dickey - Fuller testet die Nullhypothese, dass Zeitreihen Wurzeln haben und ebenfalls stationär sind, oder lehnt diese Hypothese ab. Wenn wir den Dickey-Fuller-Test auf unserer ersten Scheibe durchführen, werden wir bekommen
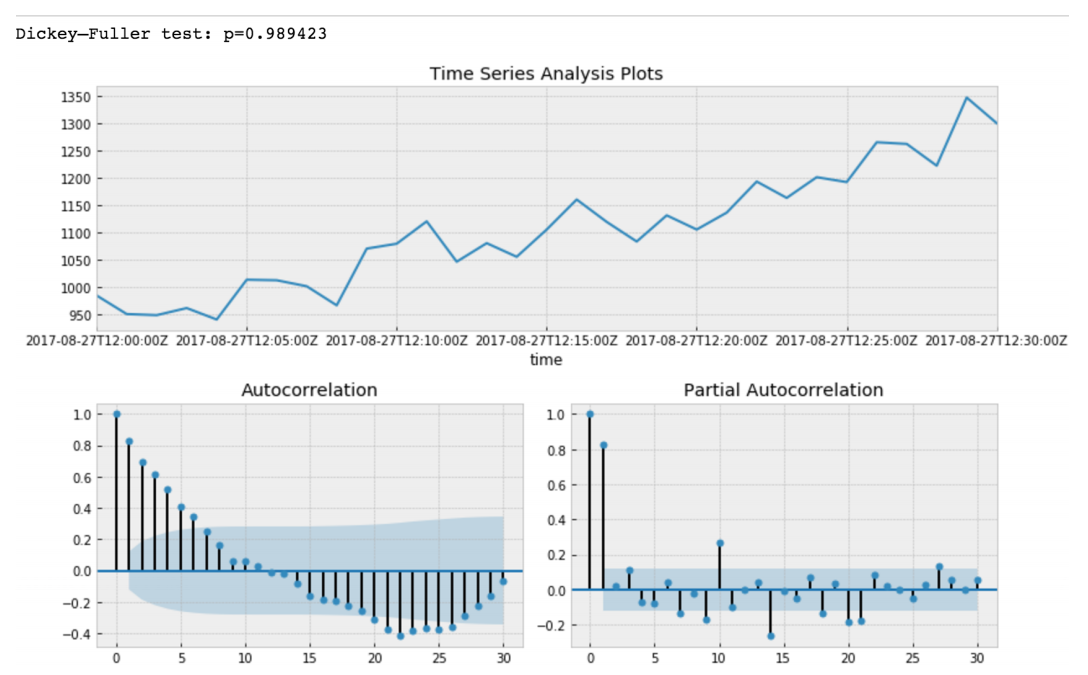
Der Wert des Dickey-Fuller-Tests lehnt eine Nullhypothese mit starker Sicherheit ab. Somit ist unsere Zeitreihenscheibe eine instationäre. Und wir können sehen, dass die Autokorrelationsfunktion versteckte Autokorrelationen zeigt.
Nach Subtraktion unseres Regressionsmodells von den Anfangsdaten.

Hier können wir sehen, dass der Dickey-Fuller-Testwert wirklich klein ist und eine Nullhypothese über die Nichtstationarität unserer Zeitreihenscheibe nicht ablehnen. Auch die Autokorrelationsfunktion sieht gut aus.
Daher haben wir einige Änderungen an unseren Daten vorgenommen und können unsere Daten entsprechend unserer Steigung unserer Trendlinie drehen.
Segmentierte Regression der Daten
Die segmentierte Regression , auch als
stückweise Regression oder "Breaked-Stick-Regression" bezeichnet, ist eine Methode in der Regressionsanalyse, bei der die unabhängige Variable in Intervalle unterteilt und ein separates Liniensegment an jedes Intervall angepasst wird. Eine segmentierte Regressionsanalyse kann auch für multivariate Daten durchgeführt werden, indem die verschiedenen unabhängigen Variablen partitioniert werden. Eine segmentierte Regression ist nützlich, wenn die unabhängigen Variablen, die in verschiedene Gruppen gruppiert sind, unterschiedliche Beziehungen zwischen den Variablen in diesen Regionen aufweisen. Die Grenzen zwischen den Segmenten sind Haltepunkte.
Tatsächlich ist unsere Steigung eine diskrete Ableitung unserer instationären Zeitreihen aufgrund des konstanten Intervalls unserer metrischen Punkte, das wir dx nicht berücksichtigen können. Daher können wir unsere Daten als stückweise Funktion approximieren, die unter Verwendung diskreter Ableitungen von Zeitreihen-Regressionstrends berechnet wurde.

Oben ist ein Datenabschnitt von 26–08–2017 00.00 bis 08.00 Uhr
Es sieht so aus, als ob es für jede Schicht eine lineare Autokorrelation gibt. Wenn wir für jede Schicht eine Regressionslinie finden, können wir ein Modell unserer Zeitscheiben unter Verwendung der von uns getroffenen Annahmen erstellen.
Als Ergebnis werden wir Daten haben, die unter Verwendung einer minimalen Anzahl von Parametern beschrieben werden, was aufgrund einer besseren Verallgemeinerung günstig ist. Die Vapnik-Chervonenkis-Dimension sollte für eine gute Verallgemeinerung so klein wie möglich sein.
In der Vapnik-Chervonenkis-Theorie ist die VC-Dimension (für die Vapnik-Chervonenkis-Dimension) ein Maß für die Kapazität (Komplexität, Ausdruckskraft, Reichhaltigkeit oder Flexibilität) eines Funktionsraums, die von einem statistischen Klassifizierungsalgorithmus gelernt werden kann. Es ist definiert als die Kardinalität der größten Menge von Punkten, die der Algorithmus zerstören kann. Es wurde ursprünglich von Vladimir Vapnik und Alexey Chervonenkis definiert.
Formal hängt die Kapazität eines Klassifizierungsmodells davon ab, wie kompliziert es sein kann. Betrachten Sie beispielsweise die Schwellenwertbildung eines hochgradigen Polynoms: Wenn das Polynom über Null liegt, wird dieser Punkt als positiv, andernfalls als negativ klassifiziert. Ein hochgradiges Polynom kann wackelig sein, sodass es gut zu einem bestimmten Satz von Trainingspunkten passt. Man kann aber erwarten, dass der Klassifikator in anderen Punkten Fehler macht, weil er zu wackelig ist. Ein solches Polynom hat eine hohe Kapazität. Eine viel einfachere Alternative besteht darin, eine lineare Funktion zu schwellen. Diese Funktion passt möglicherweise nicht gut zum Trainingsset, da es eine geringe Kapazität hat.
Infolgedessen haben wir unsere Stundenscheiben mithilfe einer segmentierten Regression angenähert.
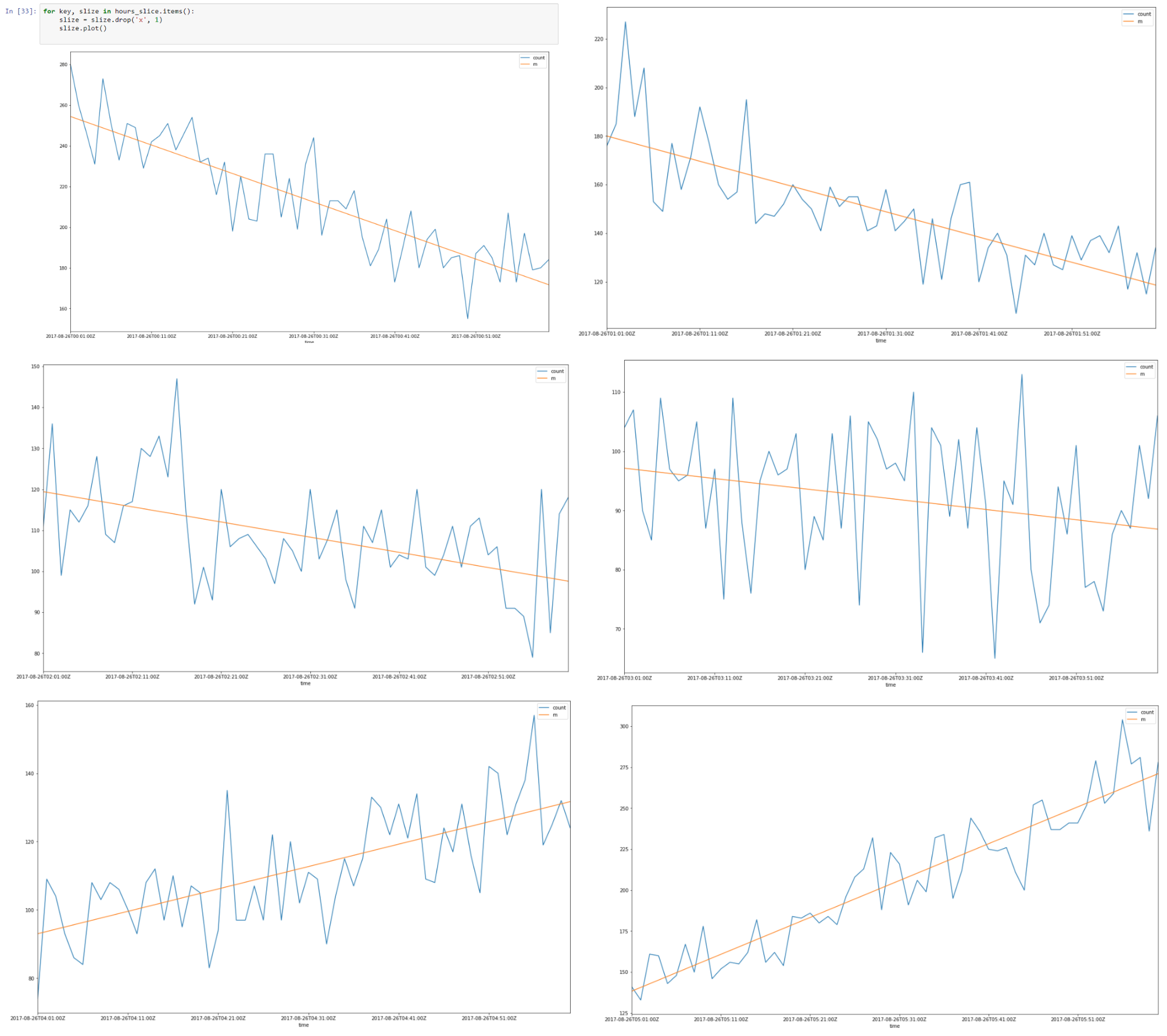
Alle 8-Stunden-Scheiben zusammensetzen

Und machen Sie es stationär stochastisch, indem Sie das Regressionsmodell subtrahieren.
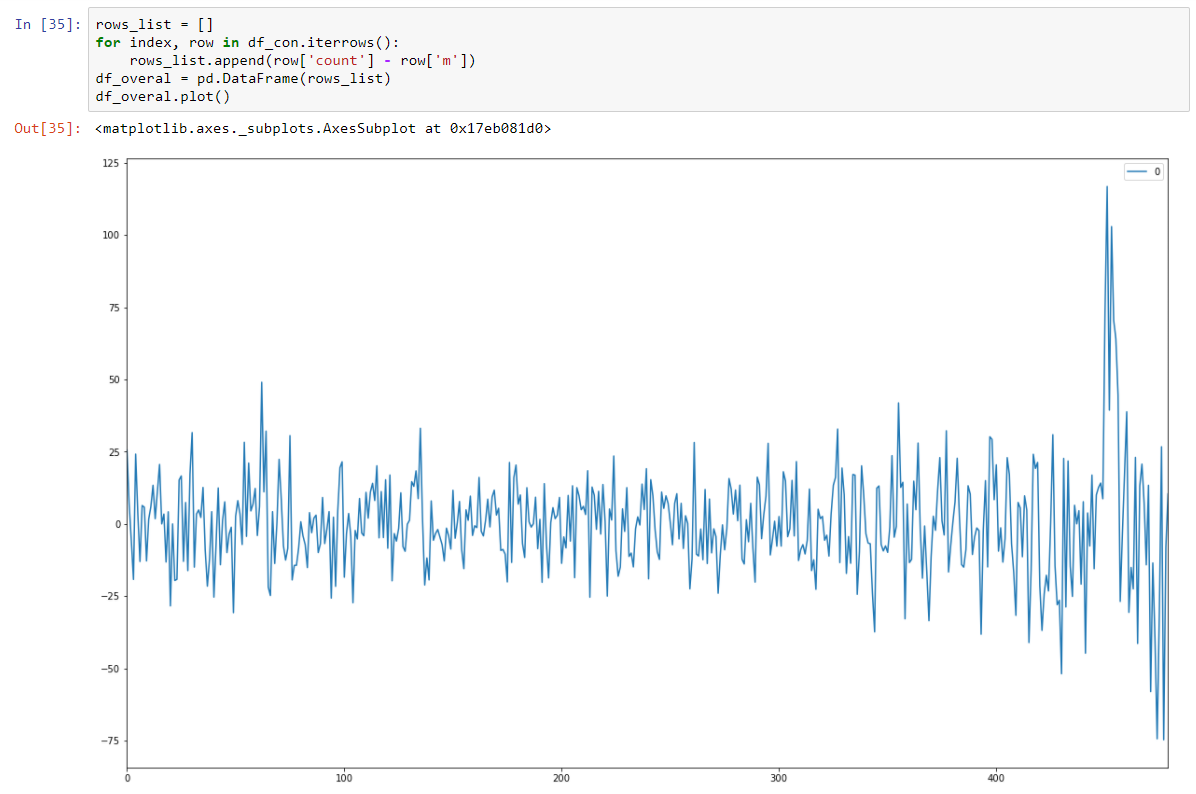
Und unser Dickey-Fuller-Test für stationäre Geräte zeigt mit großer Zuversicht, dass wir unsere Daten in stationäre Serien umgewandelt haben.
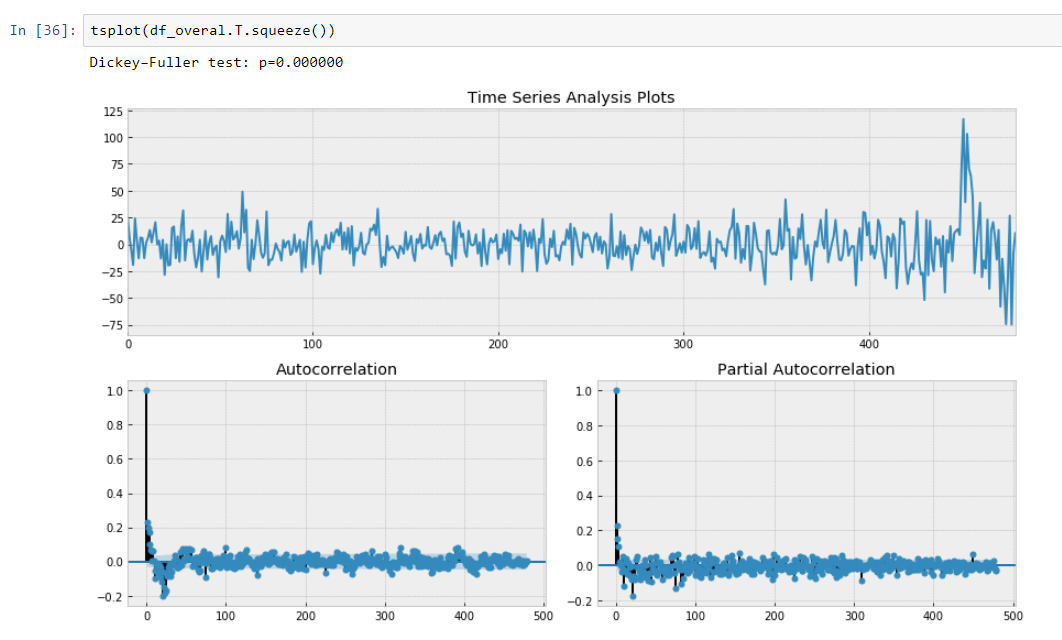
Wir haben also ein Vorhersagemodell, das unsere Zeitreihendaten beschreibt. Wir haben die Dimensionalität unserer Daten um das 15/30-fache verringert!
Eigentlich sollten wir den Mittelwert der Vorhersage unseres Modells zurückgeben und ihn unter Verwendung von Ebene und Steigung für eine bestimmte Schicht zurücktransformieren. Dadurch wird die Summe der quadratischen Fehler für die Vorhersage unserer Modelle minimiert.
Wir sollten jedoch auch die Varianz speichern, da eine Zunahme der Varianz zum Vorhandensein neuer unbekannter Faktoren führen kann, und wie wir aus dem Domänenwissen wissen, ist dies auch so.
Daher sollte auch eine schnelle Änderung der Varianz beachtet werden.
Wir möchten auch das ARIMA-Modell verwenden, aber ein allgemeinerer Ansatz ist besser, und wir planen, dieses Modell und Standard-ARIMA zu vergleichen, um bessere Ergebnisse zu erzielen. Sehen wir uns unsere Zeitreihen an (Grün sind Varianzbursts bei Ausreißern).