Hallo allerseits! Die Entwicklung des Hexapods schreitet voran und schließlich wurde der grundlegende mathematische Teil getestet und ist zur Dokumentation bereit. Damit das Projekt bis zum Ende überlebt und sich nicht im Regal verstaubt, müssen Sie die positiven Verschiebungen sehen, auch wenn sie unbedeutend sind. In diesem Artikel werde ich über einen Algorithmus zur Lösung des Problems der inversen Kinematik sprechen und ihn in Aktion demonstrieren. Ich hoffe es wird interessant.
Entwicklungsstadien:Teil 1 - DesignTeil 2 - MontageTeil 3 - KinematikTeil 4 - mathematische Trajektorien und SequenzenTeil 5 - ElektronikTeil 6 - Übergang zum 3D-DruckTeil 7 - Neues Gehäuse, Anwendungssoftware und KommunikationsprotokolleKoordinatensysteme
Zunächst müssen die Koordinatensysteme des Roboters bestimmt werden - es gibt bis zu drei davon:
Tatsächlich unterscheiden sie sich nicht voneinander, sondern befinden sich an verschiedenen Stellen des Gehäuses und können in einem bestimmten Winkel relativ zueinander gedreht werden. Von oben gesehen ist die Position der Achsen wie folgt (der Parameter coxa_zero_rotate wird etwas später beschrieben):
Wie Sie wahrscheinlich bereits bemerkt haben, befinden sich die Koordinatensysteme auf der linken und rechten Seite symmetrisch zur Körpermitte. Es schien mir, dass es einfacher sein würde.
Die Koordinaten jedes Punktes werden relativ zu dem Glied festgelegt, für das dieser Punkt bestimmt ist. Mit diesem Ansatz können Sie das Glied schmerzlos überall hin bewegen, ohne die Konfiguration zu beeinträchtigen.
Und so befinden sie sich relativ zum Glied:
Die Koordinaten des Zielpunkts beziehen sich auf das HAUPTKOORDINATENSYSTEM. Anfangs wollte ich die Koordinaten relativ zur Mitte des Falls einstellen, aber dies war nicht sehr praktisch und erforderte die Speicherung einer Reihe zusätzlicher Parameter.
Nachfolgend die Notation X *, X ** usw. wird durch X ', X' 'ersetzt.
Lösung des Problems der inversen Kinematik
Beginnen wir mit dem für mich schwierigsten und interessantesten Moment - der Kinematik. Ich habe den Algorithmus selbst erfunden und manchmal einen Blick auf die Eigenschaften eines Dreiecks und trigonometrische Funktionen geworfen. Mit der Mechanik ist es schwer für mich und mit der Trigonometrie ist es noch schlimmer. Vielleicht könnte ich irgendwo etwas nicht berücksichtigen, aber dieser Algorithmus funktioniert (Video am Ende).
1. Erklärung des Problems
Angenommen, wir brauchen das vordere rechte Glied, um Punkt A mit Koordinaten (150; -20; 100) zu erreichen. Es ist auch bekannt, dass das Glied relativ zum Körper um 45 Grad gedreht ist (Parameter coxa_zero_rotate):
Das Glied selbst hat folgende Parameter:
Ich denke, Sie müssen nicht beschreiben, was diese Parameter bedeuten, die Namen sprechen für sich. Sie können nur hinzufügen, dass alle diese Parameter durch die Konfiguration des Gehäuses bestimmt werden, permanent sind und im FLASH-Speicher gespeichert werden und von außen bearbeitet werden können (aus Gründen der Flexibilität).
Deshalb brauchst du es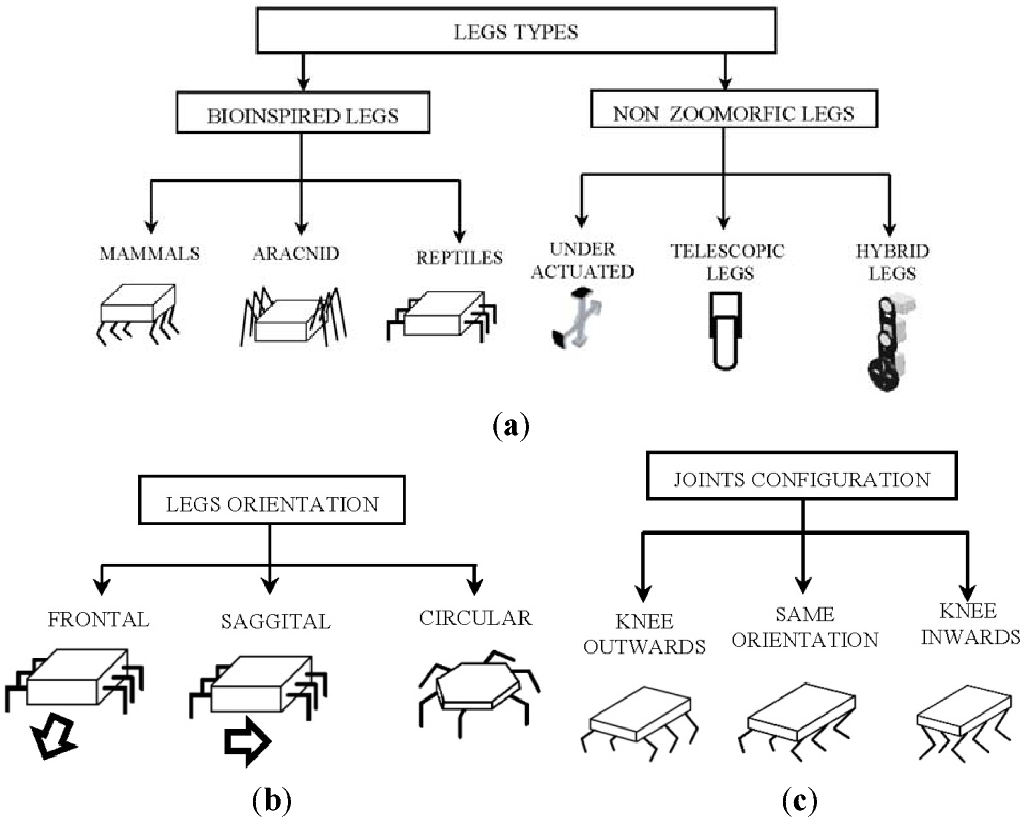
Das Bild zeigt verschiedene Variationen des Rumpfes und die Position der Beine des Hexapods. Jetzt stimmt es mit der ARACNID-Konfiguration überein. Angenommen, mir ist der Gedanke gekommen, den Fall in REPTILES zu ändern, und dafür reicht es aus, nur die Werte der Parameter ohne Messung im Programm selbst zu ändern, selbst die Zielpunkte müssen nicht geändert werden (es sei denn, dies wird natürlich korrekt angegangen).
Alle oben genannten Parameter reichen aus, um das Problem zu lösen.
2. Die Lösung des Problems
2.1 Ermitteln des Drehwinkels von COXADiese Phase ist die einfachste. Zuerst müssen Sie die Koordinaten von Punkt A relativ zum LIMB COORDINATE SYSTEM neu berechnen. Natürlich müssen Sie den Winkel coxa_zero_rotate drehen. Dies können Sie mit den folgenden Formeln tun:
$$ Anzeige $$ x ′ = x ⋅ cos (α) + z ⋅ sin (α) = 150 ⋅ cos (45) + 100 ⋅ sin (45) = 176,78 $$ Anzeige $$
y′=y=−20
$$ Anzeige $$ z ′ = -x ⋅ sin (α) + z ⋅ cos (α) = -150 ⋅ sin (45) + 100 ⋅ cos (45) = -35,36 $$ Anzeige $$
Somit haben wir die Koordinaten des Zielpunkts A (176,78; -20; -35,36) relativ zum LIMB-KOORDINATENSYSTEM erhalten.
Jetzt können Sie den COXA-Winkel mit der atan2-Funktion ermitteln:
COXA=atan2(z′,x′)=atan2(−35,36,176,78)=−11,30°
Wir haben also den Winkel erhalten, um den Sie das COXA-Servo drehen müssen, damit Punkt A in der X'Y'-Ebene liegt. Lassen Sie uns nun unsere Berechnungen in KOMPAS 3D überprüfen:
Alles ist richtig.
2.2 Ermitteln des Drehwinkels von FEMUR und TIBIAUm diese Winkel zu finden, muss man zur X'Y'-Ebene gehen. Um zur Ebene zu gelangen, müssen Sie den Punkt um den Winkel COXA drehen, den wir bereits zuvor berechnet haben.
$$ Anzeige $$ x '= x' ⋅ cos (α) + y '⋅ sin (α) = 176,78 ⋅ cos (-11) + -20 ⋅ sin (-11) = 180,28 $$ Anzeige $$
y′=y=−20
Die
y'- Koordinate ändert sich nicht, wenn wir uns entlang der Y'-Achse drehen.
Als nächstes müssen Sie die COXA-Länge aus der Berechnung entfernen, d. H. wir gehen zur Ebene X''Y '' über, dafür führen wir eine Verschiebung der Koordinate
x 'des Punktes um die Länge COXA durch:
x″=x′−coxaLength=180,28−40=140,28
y″=y′
Nach all diesen Manipulationen reduziert sich die weitere Lösung des Problems darauf, die Winkel
a und
b des Dreiecks zu finden:
Bevor Sie die Winkel finden, müssen Sie die dritte Seite C dieses Dreiecks finden. Dieser Abstand ist nichts anderes als die Länge des Vektors und wird nach folgender Formel berechnet:
$$ Anzeige $$ C = \ sqrt {x '' ^ 2 + y '' ^ 2} = \ sqrt {140,28 ^ 2 + (-20) ^ 2} = 141,70 $$ Anzeige $$
Jetzt müssen Sie prüfen, ob das Glied diesen Punkt erreichen kann. Wenn C größer ist als die Summe der Längen von FEMUR und TIBIA, ist der Punkt nicht erreichbar. In unserem Fall 141,70 <141 + 85 - der Punkt ist erreichbar.
Jetzt kennen wir alle Seiten des Dreiecks und können die benötigten Winkel
a und
b mithilfe des Kosinussatzes finden:
a=acos(A2+C2−B2 über2AC)=72,05°
b=acos(B2+A2−C2 über2BA)=72,95°
Die erhaltenen Winkel gelten nicht für die Zuführung zu Servos, da dies die Anfangsposition und den Neigungswinkel der Geraden C zur X-Achse nicht berücksichtigt. Wenn wir die Anfangswinkel FEMUR und TIBIA (135 ° und 45 °) kennen, ist der Neigungswinkel C zur X-Achse nicht bekannt. Sie finden es mit der Funktion atan2 (y ′ ′, x ′ ′):
$$ Anzeige $$ φ = atan2 (y '', x '') = atan2 (-20, 140,28) = -8,11 ° $$ Anzeige $$
Schließlich können Sie den Drehwinkel der Servos FEMUR und TIBIA berechnen:
FEMUR=femurZeroRotate−a−φ=135−72,05+8,11=71,06°
FEMUR=b−tibiaZeroRotate=45−72,95=27,95°
Lassen Sie uns unsere Berechnungen überprüfen:
Es scheint wie die Wahrheit.
Zusammenfassung
Die berechneten Winkel COXA, FEMUR und TIBIA eignen sich zur Fütterung ihrer Servos. Möglicherweise stellen Sie fest, dass der COXA-Winkel negativ ist, und dementsprechend stellt sich die Frage: „Wie dreht man den Antrieb um -11,3 Grad?“. Der Trick ist, dass ich die neutrale Position des COXA-Servos als logische Null verwende. Dadurch kann der Antrieb sowohl positive als auch negative Winkel drehen. Dies ist natürlich offensichtlich, aber ich denke, es wäre nicht unangebracht, dies zu erwähnen. Ich werde in den folgenden Artikeln ausführlicher darauf eingehen, wenn ich über die Implementierung all dieser Punkte spreche.
Quellcode
Genug der Worte, lassen Sie mich den Code sehen#define RAD_TO_DEG(rad) ((rad) * 180.0 / M_PI) #define DEG_TO_RAD(deg) ((deg) * M_PI / 180.0) typedef enum { LINK_COXA, LINK_FEMUR, LINK_TIBIA } link_id_t; typedef struct {
Algorithmus in Aktion
Dann erschien zufällig eine Sequenz, die etwas an einen Tanz erinnerte
PS
Ich würde mich freuen, wenn jemand diesen Algorithmus vereinfachen kann. Ich habe es so gemacht, dass ich es nach etwa einem halben Jahr verstehen konnte.