In unserer Zeit haben Maschinen eine Genauigkeit von 99% beim Verstehen und Definieren von Merkmalen und Objekten in Bildern erreicht. Wir sind jeden Tag damit konfrontiert, zum Beispiel: Gesichtserkennung in der Kamera des Smartphones, die Möglichkeit, bei Google nach Fotos zu suchen, Text aus einem Barcode oder Büchern mit einer guten Geschwindigkeit zu scannen usw. Diese Effizienz der Maschine wurde durch ein spezielles neuronales Netzwerk ermöglicht, das als Faltungs-Neuronales bezeichnet wird das Netzwerk. Wenn Sie ein Deep-Learning-Enthusiast sind, haben Sie wahrscheinlich davon gehört, und Sie könnten mehrere Bildklassifizierer entwickeln. Moderne Deep-Learning-Frameworks wie Tensorflow und PyTorch vereinfachen das maschinelle Lernen von Bildern. Es bleibt jedoch die Frage: Wie passieren die Daten die Schichten des neuronalen Netzwerks und wie lernt der Computer daraus? Um eine klare Sicht von Grund auf zu erhalten, tauchen wir in eine Faltung ein und visualisieren das Bild jeder Ebene.

Faltungsneurale Netze
Bevor Sie mit dem Studium von Convolutional Neural Networks (SNA) beginnen, müssen Sie lernen, wie Sie mit neuronalen Netzen arbeiten. Neuronale Netze ahmen das menschliche Gehirn nach, um komplexe Probleme zu lösen und nach Mustern in Daten zu suchen. In den letzten Jahren haben sie viele Algorithmen für maschinelles Lernen und Computer Vision ersetzt. Das Grundmodell eines neuronalen Netzwerks besteht aus Neuronen, die in Schichten organisiert sind. Jedes neuronale Netzwerk verfügt über eine Eingabe- und Ausgabeschicht und mehrere verborgene Schichten, die je nach Komplexität des Problems hinzugefügt werden. Bei der Übertragung von Daten durch Schichten werden Neuronen trainiert und erkennen Zeichen. Diese Darstellung eines neuronalen Netzwerks wird als Modell bezeichnet. Nachdem das Modell trainiert wurde, bitten wir das Netzwerk, Prognosen basierend auf Testdaten zu erstellen.
Der SNS ist ein spezielles neuronales Netzwerk, das gut mit Bildern funktioniert. Ian Lekun schlug sie 1998 vor, wo sie die im Eingabebild vorhandene Nummer erkannten. SNA wird auch zur Spracherkennung, Bildsegmentierung und Textverarbeitung verwendet. Vor der Schaffung von Faltungs-Neuronalen Netzen wurden mehrschichtige Perzeptrone bei der Konstruktion von Bildklassifikatoren verwendet. Die Bildklassifizierung bezieht sich auf die Aufgabe, Klassen aus einem Mehrkanal-Rasterbild (Farbe, Schwarzweiß) zu extrahieren. Mehrschichtige Perzeptrone benötigen viel Zeit, um nach Informationen in Bildern zu suchen, da jede Eingabe jedem Neuron in der nächsten Schicht zugeordnet werden muss. Die SNA ging um sie herum und verwendete ein Konzept namens lokale Konnektivität. Dies bedeutet, dass wir jedes Neuron nur mit der lokalen Eingangsregion verbinden. Dies minimiert die Anzahl der Parameter und ermöglicht es verschiedenen Teilen des Netzwerks, sich auf übergeordnete Attribute wie Textur oder sich wiederholendes Muster zu spezialisieren. Verwirrt? Vergleichen wir, wie Bilder über mehrschichtige Perzeptrone (MPs) und Faltungs-Neuronale Netze übertragen werden.
Vergleich von MP und SNA
Die Gesamtzahl der Einträge in der Eingabeebene für das mehrschichtige Perzeptron beträgt 784, da das Eingabebild eine Größe von 28 x 28 = 784 hat (der MNIST-Datensatz wird berücksichtigt). Das Netzwerk sollte in der Lage sein, die Anzahl im Eingabebild vorherzusagen. Dies bedeutet, dass die Ausgabe zu einer der folgenden Klassen im Bereich von 0 bis 9 gehören kann. In der Ausgabeschicht geben wir Klassenschätzungen zurück, z. B. wenn diese Eingabe das Bild mit der Nummer „3“ ist. dann hat in der Ausgabeschicht das entsprechende Neuron "3" einen höheren Wert als andere Neuronen. Wieder stellt sich die Frage: "Wie viele versteckte Schichten brauchen wir und wie viele Neuronen sollten in jeder sein?" Nehmen Sie zum Beispiel den folgenden MP-Code:
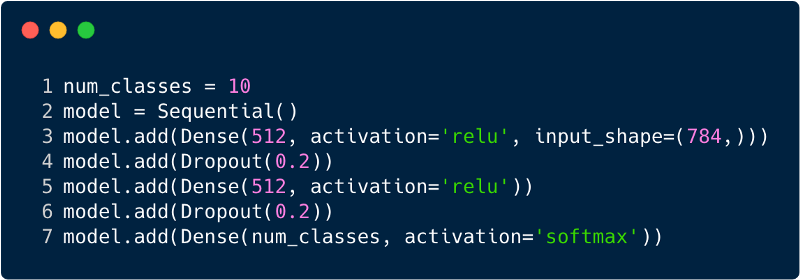
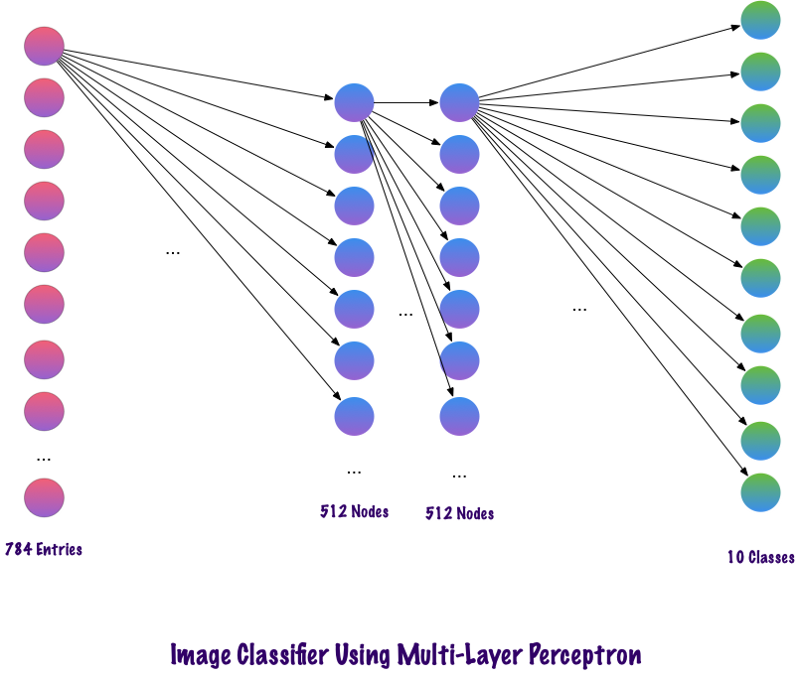
Der obige Code wird mithilfe eines Frameworks namens Keras implementiert. Die erste verborgene Schicht hat 512 Neuronen, die mit der Eingangsschicht von 784 Neuronen verbunden sind. Die nächste verborgene Schicht: die Ausschlussschicht, die das Problem der Umschulung löst. 0,2 bedeutet, dass eine Wahrscheinlichkeit von 20% besteht, die Neuronen der vorherigen verborgenen Schicht nicht zu berücksichtigen. Wir haben erneut eine zweite verborgene Schicht mit der gleichen Anzahl von Neuronen wie in der ersten verborgenen Schicht (512) und dann eine weitere exklusive Schicht hinzugefügt. Beenden Sie diesen Satz von Ebenen mit einer Ausgabeebene, die aus 10 Klassen besteht. Die Klasse, die am wichtigsten ist, ist die vom Modell vorhergesagte Anzahl. So sieht ein mehrschichtiges Netzwerk aus, nachdem alle Schichten identifiziert wurden. Einer der Nachteile des mehrstufigen Perzeptrons besteht darin, dass es vollständig verbunden ist, was viel Zeit und Raum in Anspruch nimmt.
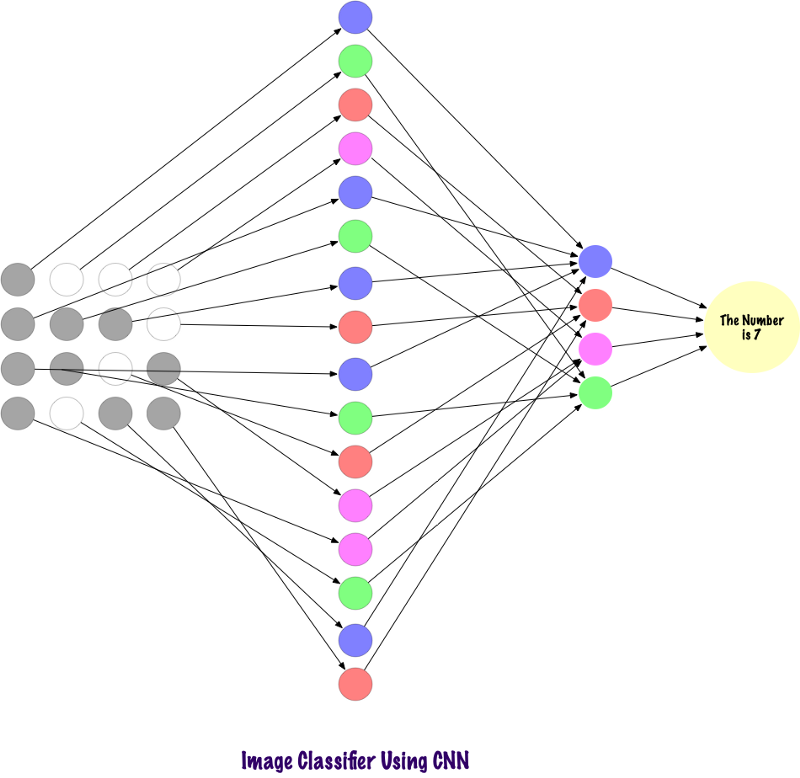
Convolts verwenden keine vollständig verbundenen Schichten. Sie verwenden spärliche Schichten, die Matrizen als Eingabe verwenden, was einen Vorteil gegenüber MP bietet. In MP ist jeder Knoten dafür verantwortlich, das gesamte Bild zu verstehen. In der SNA teilen wir das Bild in Bereiche (kleine lokale Bereiche von Pixeln) auf. Die Ausgabeschicht kombiniert die empfangenen Daten von jedem versteckten Knoten, um Muster zu finden. Unten sehen Sie ein Bild davon, wie die Ebenen verbunden sind.
Nun wollen wir sehen, wie die SNA Informationen auf Fotos findet. Vorher müssen wir verstehen, wie die Zeichen extrahiert werden. In der SNA verwenden wir verschiedene Ebenen. Jede Ebene bewahrt die Zeichen des Bildes. Beispielsweise berücksichtigt sie das Bild des Hundes. Wenn das Netzwerk den Hund klassifizieren muss, muss es alle Zeichen wie Augen, Ohren, Zunge, Beine usw. identifizieren. Diese Zeichen werden auf lokaler Netzwerkebene mithilfe von Filtern und Kernen unterbrochen und erkannt.
Wie sehen Computer ein Bild aus?
Eine Person, die ein Bild betrachtet und seine Bedeutung versteht, klingt sehr vernünftig. Nehmen wir an, Sie gehen und bemerken die vielen Landschaften um Sie herum. Wie verstehen wir die Natur in diesem Fall? Wir fotografieren die Umwelt mit unserem Hauptsinnesorgan - dem Auge - und senden es dann an die Netzhaut. Es sieht alles ziemlich interessant aus, oder? Stellen wir uns nun vor, dass ein Computer dasselbe tut. In Computern werden Bilder mit einer Reihe von Pixelwerten interpretiert, die zwischen 0 und 255 liegen. Der Computer betrachtet diese Pixelwerte und versteht sie. Auf den ersten Blick kennt er keine Objekte und Farben. Es erkennt einfach die Pixelwerte und das Bild entspricht einer Reihe von Pixelwerten für den Computer. Später lernt er durch Analyse der Pixelwerte nach und nach, ob das Bild grau oder farbig ist. Bilder in Graustufen haben nur einen Kanal, da jedes Pixel die Intensität einer Farbe darstellt. 0 bedeutet schwarz und 255 bedeutet weiß, die anderen Varianten von schwarz und weiß, dh grau, liegen zwischen ihnen.
Farbbilder haben drei Kanäle: Rot, Grün und Blau. Sie repräsentieren die Intensität von 3 Farben (dreidimensionale Matrix), und wenn sich die Werte gleichzeitig ändern, ergibt sich eine große Anzahl von Farben, wirklich eine Farbpalette! Danach erkennt der Computer die Kurven und Konturen von Objekten im Bild. All dies kann im Faltungsnetzwerk untersucht werden. Dazu verwenden wir PyTorch, um einen Datensatz zu laden und Filter auf Bilder anzuwenden. Das Folgende ist ein Codeausschnitt.
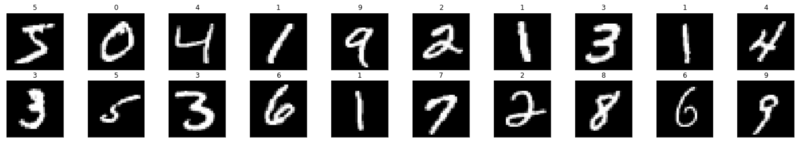
Nun wollen wir sehen, wie ein einzelnes Bild in ein neuronales Netzwerk eingespeist wird.
img = np.squeeze(images[7]) fig = plt.figure(figsize = (12,12)) ax = fig.add_subplot(111) ax.imshow(img, cmap='gray') width, height = img.shape thresh = img.max()/2.5 for x in range(width): for y in range(height): val = round(img[x][y],2) if img[x][y] !=0 else 0 ax.annotate(str(val), xy=(y,x), color='white' if img[x][y]<thresh else 'black')

Auf diese Weise wird die Zahl „3“ in Pixel aufgeteilt. Aus dem Satz handgeschriebener Ziffern wird zufällig „3“ ausgewählt, in dem Pixelwerte angezeigt werden. Hier normalisiert ToTensor () die tatsächlichen Pixelwerte (0–255) und begrenzt sie auf einen Bereich von 0 bis 1. Warum ist das so? Weil es die Berechnungen in den folgenden Abschnitten erleichtert, entweder um Bilder zu interpretieren oder um gemeinsame Muster zu finden, die in ihnen vorhanden sind.
Erstellen Sie Ihren eigenen Filter
Filter filtern, wie der Name schon sagt, Informationen. Bei Faltungs-Neuronalen Netzen werden beim Arbeiten mit Bildern Informationen über die Pixel gefiltert. Warum sollten wir überhaupt filtern? Denken Sie daran, dass ein Computer einen Lernprozess durchlaufen muss, um Bilder zu verstehen, ähnlich wie es ein Kind tut. In diesem Fall brauchen wir jedoch nicht viele Jahre! Kurz gesagt, er lernt von Grund auf neu und rückt dann zum Ganzen vor.
Daher sollte das Netzwerk zunächst alle groben Teile des Bildes kennen, nämlich die Kanten, Konturen und andere Elemente auf niedriger Ebene. Sobald sie entdeckt wurden, ist der Weg für komplexe Symptome geebnet. Um zu ihnen zu gelangen, müssen wir zuerst die Attribute auf niedriger Ebene extrahieren, dann die Attribute auf mittlerer und dann auf höherer Ebene. Filter sind eine Möglichkeit, die Informationen zu extrahieren, die der Benutzer benötigt, und nicht nur die blinde Datenübertragung, aufgrund derer der Computer die Strukturierung von Bildern nicht versteht. Zu Beginn können Funktionen auf niedriger Ebene basierend auf einem bestimmten Filter extrahiert werden. Der Filter ist hier auch eine Reihe von Pixelwerten, ähnlich einem Bild. Es kann als die Gewichte verstanden werden, die die Schichten in dem Faltungs-Neuronalen Netzwerk verbinden. Diese Gewichte oder Filter werden mit Eingabewerten multipliziert, um Zwischenbilder zu erzeugen, die das Computerverständnis des Bildes darstellen. Dann werden sie mit einigen weiteren Filtern multipliziert, um die Ansicht zu erweitern. Dann erkennt es die sichtbaren Organe einer Person (vorausgesetzt, eine Person ist im Bild vorhanden). Später, mit mehreren weiteren Filtern und mehreren Schichten, ruft der Computer aus: „Oh, ja! Das ist ein Mann. "
Wenn wir über Filter sprechen, haben wir viele Möglichkeiten. Möglicherweise möchten Sie das Bild verwischen und dann einen Unschärfefilter anwenden. Wenn Sie Schärfe hinzufügen müssen, hilft ein Schärfefilter usw.
Schauen wir uns einige Codefragmente an, um die Funktionalität von Filtern zu verstehen.
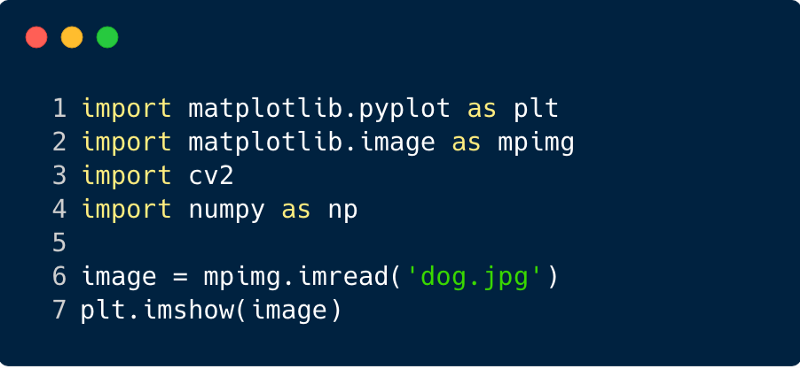

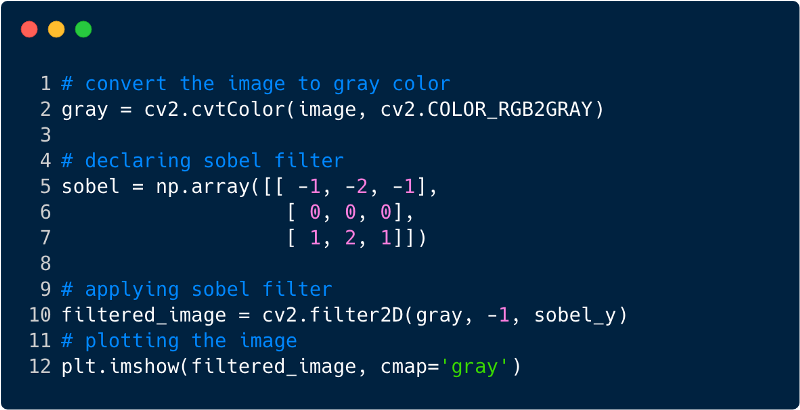

So sieht das Bild nach dem Anwenden des Filters aus. In diesem Fall haben wir den Sobel-Filter verwendet.
Faltungsneurale Netze
Bisher haben wir gesehen, wie Filter verwendet werden, um Features aus Bildern zu extrahieren. Um das gesamte neuronale Faltungsnetzwerk zu vervollständigen, müssen wir alle Schichten kennen, die wir zum Entwerfen verwenden. Die in der SNA verwendeten Schichten,
- Faltungsschicht
- Pooling-Schicht
- Vollständig verklebte Schicht
Bei allen drei Ebenen sieht der Faltungsbildklassifizierer folgendermaßen aus:
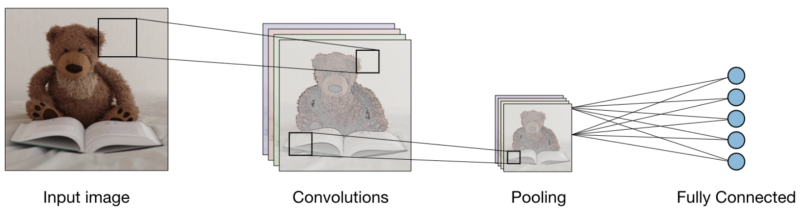
Nun wollen wir sehen, was jede Ebene tut.
Die Faltungsschicht (CONV) verwendet Filter, die Faltungsoperationen ausführen, indem sie das Eingabebild scannen. Seine Hyperparameter umfassen eine Filtergröße, die 2x2, 3x3, 4x4, 5x5 (aber nicht darauf beschränkt) sein kann, und Schritt S. Das Ergebnis O wird als Feature-Map oder Aktivierungs Map bezeichnet, in der alle Features mithilfe von Eingabeebenen und Filtern berechnet werden. Unten sehen Sie ein Bild der Generierung von Feature-Maps beim Anwenden der Faltung
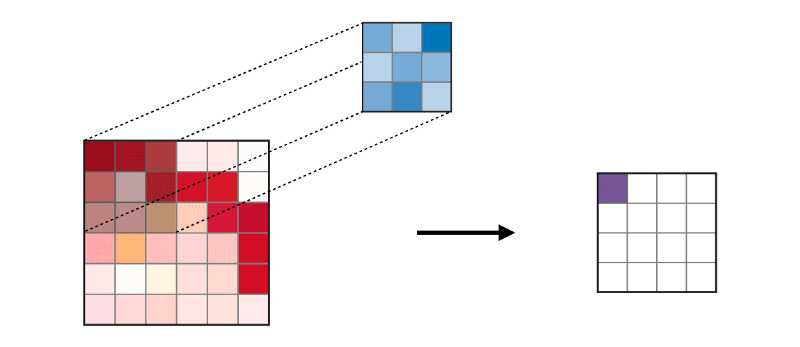 Die Zusammenführungsschicht (POOL) wird
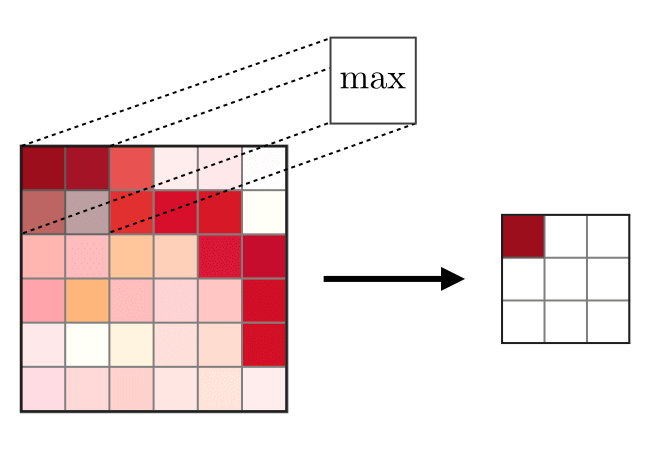
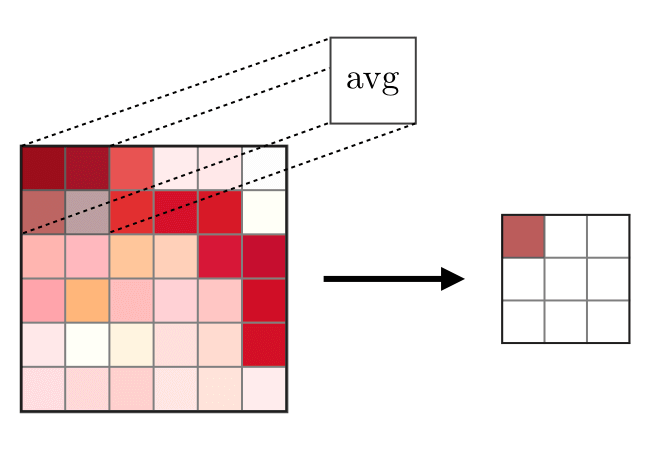
Die Zusammenführungsschicht (POOL) wird verwendet, um die Merkmale zu komprimieren, die typischerweise nach der Faltungsschicht verwendet werden. Es gibt zwei Arten von Gewerkschaftsoperationen: Dies ist die maximale und durchschnittliche Vereinigung, bei der die maximalen und durchschnittlichen Werte der Merkmale verwendet werden. Das Folgende ist die Operation von Zusammenführungsoperationen
 Vollständig verbundene Schichten (FCs)
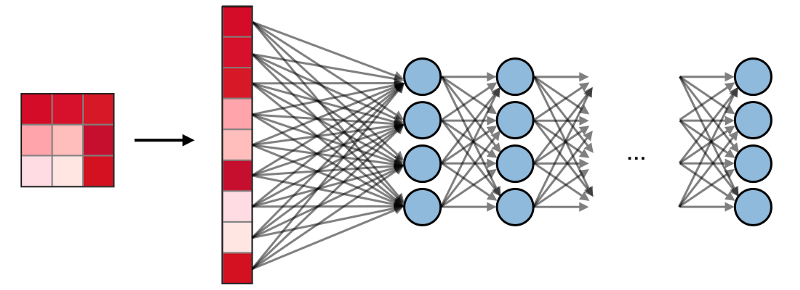
Vollständig verbundene Schichten (FCs) arbeiten mit einem flachen Eingang, wobei jeder Eingang mit allen Neuronen verbunden ist. Sie werden normalerweise am Ende des Netzwerks verwendet, um verborgene Schichten mit der Ausgabeschicht zu verbinden, wodurch die Klassenwerte optimiert werden.
SNA-Visualisierung in PyTorch
Nachdem wir nun die vollständige Ideologie zum Erstellen des SNA haben, implementieren wir den SNA mithilfe des PyTorch-Frameworks von Facebook.
Schritt 1 : Laden Sie das Eingabebild herunter, das über das Netzwerk gesendet werden soll. (Hier machen wir es mit Numpy und OpenCV)
import cv2 import matplotlib.pyplot as plt %matplotlib inline img_path = 'dog.jpg' bgr_img = cv2.imread(img_path) gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
 Schritt 2
Schritt 2 : Filter rendern
Lassen Sie uns die Filter visualisieren, um besser zu verstehen, welche wir verwenden werden.
import numpy as np filter_vals = np.array([ [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1] ]) print('Filter shape: ', filter_vals.shape)
 Schritt 3
Schritt 3 : Bestimmen Sie die SNA
Dieser SNS hat eine Faltungsschicht und eine Poolschicht mit einer maximalen Funktion, und die Gewichte werden unter Verwendung der oben gezeigten Filter initialisiert
import torch import torch.nn as nn import torch.nn.functional as F class Net(nn.Module): def __init__(self, weight): super(Net, self).__init__()
Net( (conv): Conv2d(1, 4, kernel_size=(4, 4), stride=(1, 1), bias=False) (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) )
Schritt 4 : Filter rendern
Ein kurzer Blick auf die verwendeten Filter,
def viz_layer(layer, n_filters= 4): fig = plt.figure(figsize=(20, 20)) for i in range(n_filters): ax = fig.add_subplot(1, n_filters, i+1) ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray') ax.set_title('Output %s' % str(i+1)) fig = plt.figure(figsize=(12, 6)) fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05) for i in range(4): ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[]) ax.imshow(filters[i], cmap='gray') ax.set_title('Filter %s' % str(i+1)) gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
Filter:
 Schritt 5
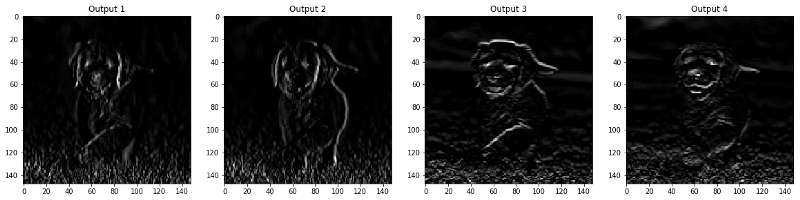
Schritt 5 : Gefilterte Ergebnisse nach Ebene
Die Bilder, die in der Ebene CONV und POOL angezeigt werden, werden unten angezeigt.
viz_layer(activated_layer) viz_layer(pooled_layer)
Faltungsschichten

Ebenen bündeln
 Quelle
Quelle