Die Problemstellung

Ich habe neulich im Internet gesurft und mir ist etwas ziemlich Merkwürdiges aufgefallen: der Mendocino-Motor . Es ist ein extrem reibungsarmer Lagerrotor: Der ursprüngliche hatte einen Glaszylinder, der an zwei Nadeln hing, aber die modernen verwenden eine Magnetfederung. Es ist ein bürstenloser Motor: An den Rotor sind Solarbatterien angeschlossen, die Strom für die um den Rotor gewickelten Spulen erzeugen. Der Rotor dreht sich in einem festen Magnetfeld, wobei die Solarbatterien nacheinander der Lichtquelle ausgesetzt werden. Es ist eine ziemlich elegante Lösung, die zu Hause sehr gut nachgebildet werden kann.

Hier ist das Video, das erklärt, wie es funktioniert (auf Russisch):


Aber dieses Video hatte eine andere Neugier, die noch stärker war als der Motor selbst. In der Videobeschreibung schreibt Dmitry Korzhevsky: „Sie können die Seitenstütze NICHT durch einen Magneten ersetzen! Frag mich nicht mehr danach! “

Hinweis: Ich bin kein Physikexperte und kann in einigen Dingen sehr falsch liegen. Korrekturen sind daher willkommen.



Lassen Sie uns noch einmal diskutieren, wie das magnetische Aufhängungssystem des Rotors funktioniert. Wenn wir zwei Magnete nehmen, sieht die potenzielle Isolinie je nach Abstand zwischen den Magneten folgendermaßen aus:



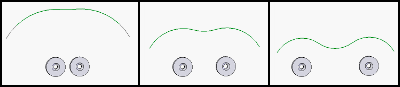
Also setzen wir zwei feste Magnete auf einen Stator. Der auf der Rotorachse platzierte Magnet möchte sich nicht seitwärts bewegen, da die potenzielle Isolinie einen bestimmten lokalen Mindestpunkt hat. Stattdessen möchte es entlang der Rotorachse herausspringen. Wir stellen zwei dieser Systeme her und am Ende ist die Rotorachse radial stabil, aber seitlich instabil. Wir beheben dies, indem wir den Rotor gegen eine Glaswand kippen und voila - wir haben ein reibungsarmes Lager.

Aber die Glaswand ist ein bisschen ... nicht ästhetisch ansprechend, nicht wahr? Es ist nur logisch, dass wir den Rotor ohne solche mechanischen Krücken vollständig in der Luft aufhängen möchten. Und offensichtlich wurde Dmitry auch mit der gleichen Frage bombardiert, weshalb er direkt in der Beschreibung beachten musste, dass es unmöglich ist. Und ich wette, Dmitry ist nicht der einzige, der es satt hat.

Lassen Sie uns das sehen , zitiere ich:

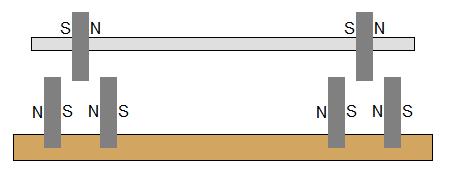
Was würde passieren, wenn die Basismagnete wie in dieser Zeichnung beabstandet und ausgerichtet wären? Würde es ihm Stabilität in der axialen Ebene geben und die Spiegelanforderung beseitigen?

Oder hier zitiere ich:

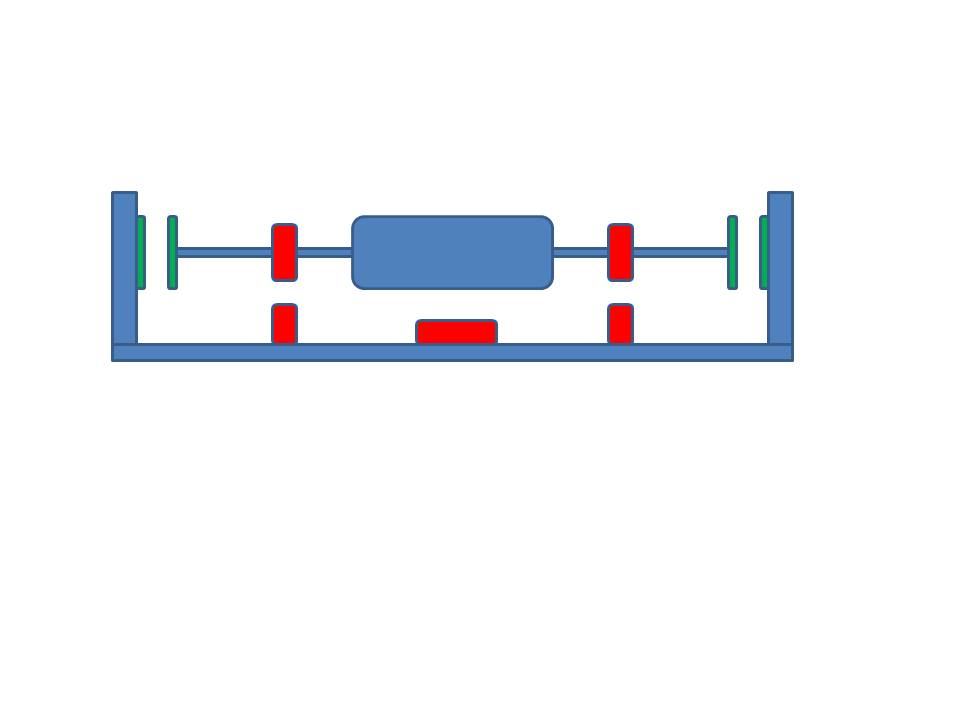
Warum schwimmt bei einem Mendocino-Motor eine Seite frei, während die andere eine Spitze an einer Wand hat? Ich weiß, dass die Frage vielleicht trivial klingt, aber ich habe mir die Idee ausgedacht, warum nicht dieselben Magnete verwendet werden, die zum Schweben als Gegenkraft auf beiden Seiten des Schafts verwendet werden. Ich habe ein sehr grobes JPG von dem angehängt, was ich meine. Die grünen Magnete am Ende der Wellen sind das, worauf ich mich beziehe. Gibt es eine Theorie oder ein Gesetz, das dies verhindert?

Wir können sehen, dass viele Menschen auf der ganzen Welt diesen unpassenden mechanischen Teil loswerden wollen. Ich habe in meiner Schulzeit nicht viel Aufmerksamkeit geschenkt, daher war mir überhaupt nicht klar, warum ein vollständig stabiles magnetisches Aufhängungssystem nicht realisierbar war. Eines Tages beim Mittagessen stellte ich meinem Vorgesetzten, einem weltberühmten Wissenschaftler (in angewandter Mathematik, nicht in Physik), diese Frage: „Warum ist das unmöglich?“. Und weißt du was, er wusste es auch nicht!

Die oben genannten Foren haben diese Frage ebenfalls nicht richtig beantwortet. Im besten Fall bezog sich jemand auf etwas, das Earnshaws Theorem genannt wurde und sich auf den ersten Blick nicht zum Verstehen eignet. Darin heißt es: Eine Sammlung von Punktladungen kann nicht allein durch die elektrostatische Wechselwirkung der Ladungen in einer stabilen stationären Gleichgewichtskonfiguration gehalten werden. Hast du es bekommen? Ich habe es bestimmt nicht getan. Nehmen wir an, ich kann die Tatsache akzeptieren, dass es sich um Ladungen und nicht um Magnete handelt. Was dann?

Erste Illustration

Wenn ich meinen Kopf nicht um etwas wickeln kann, neige ich dazu, es zu zeichnen. Lassen Sie uns dies der Einfachheit halber in 2D veranschaulichen. Stellen Sie sich vier feste Gebühren in einem quadratischen Muster sowie eine kostenlose Gebühr in der Mitte vor. So:



Ist die freie Ladung dann nicht im Gleichgewicht? Egal wo es sich bewegt, es nähert sich einer der festen Ladungen, was die Schubkraft erhöht! Versuchen wir, eine Karte der potenziellen Energie einer kostenlosen Ladung zu zeichnen. Ich habe viele Physikstunden in der Schule verpasst, daher ist Wikipedia mein Wissensspeicher dort. Wenn Sie also nur eine feste Ladung haben, erzeugt sie in dem sie umgebenden Feld ein elektrostatisches Potential :

Die Gleichung für das elektrostatische Potential (oder Coulomb-Potential) einer Punktladung im Vakuum:

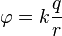
In allen meinen Gedankenexperimenten sind alle Koeffizienten entweder 0 oder 1. Die q-Ladung ist also 1 und das unbekannte k ist auch 1. Das bedeutet, dass eine feste Ladung eine potentielle Energie erzeugt, die als 1 / r gemessen wird, wobei r der Abstand zum ist aufladen.

In unserem Fall beträgt die potentielle Energie der freien Ladung innerhalb des Feldes der festen Ladung ebenfalls 1 / r. (Um fair zu sein, ist die Energie gleich k * q1 * q2 / r, aber wir wählen die Koeffizienten aus, um die Berechnungen zu vereinfachen). Bei mehreren Gebühren addieren wir einfach alle Potenziale.

Zeichnen wir eine Karte der potenziellen Energie unserer kostenlosen Ladung. Ich benutze Salbei dafür:

var('x,y') def unit_potential(a,b,x,y): return 1/(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Da ist unsere Karte. An weißen (durchstochenen) Punkten geht die potentielle Energie unendlich:



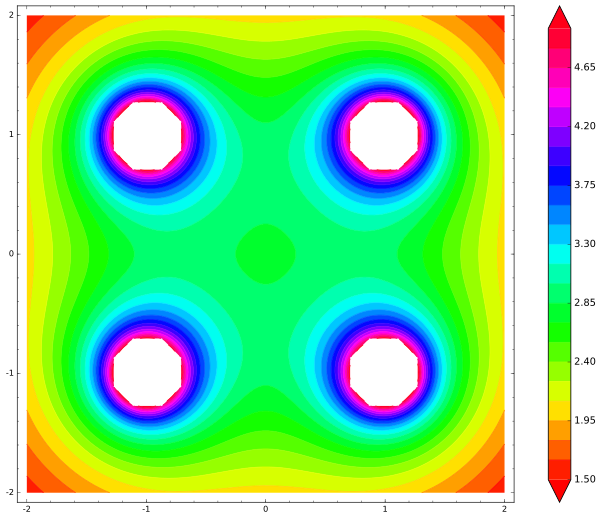
Wir sehen deutlich das lokale Minimum an Energie im Zentrum. Wo immer sich die Mittelladung bewegen will, steigt die Energie, so dass kleine Störungen sie zurück ins Zentrum zwingen - den Punkt des stabilen Gleichgewichts. War Earnshaw also falsch? Nein, war er nicht, ich habe die Illustration nur falsch gezeichnet. Und das ist ein häufiger Fehler bei Menschen, die diese Frage stellen. Halten Sie jetzt für ein paar Minuten inne und raten Sie mal: Was habe ich vermisst?

Tatsächlich bestand in diesem Fall der Fehler darin, dass in einem zweidimensionalen Raum die feste Ladung eine potentielle Energie erzeugt, die als -ln r gemessen wird, wobei r der Abstand zur Ladung ist und nicht 1 / r. Nehmen Sie vorerst einfach mein Wort und lassen Sie mich die Gleichung korrigieren, ohne viel zu erklären. Der richtige Code sieht folgendermaßen aus:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Und das ist die Karte, die es produziert:



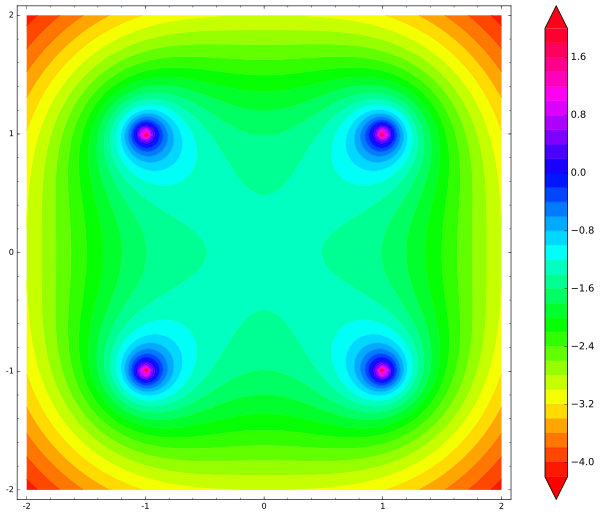
Beachten Sie, dass es nirgendwo ein lokales Minimum gibt. Das Zentrum ist der Sattelpunkt oder der Punkt des instabilen Gleichgewichts. Sobald sich die kostenlose Ladung auch nur einen Mikrometer vom Zentrum entfernt, fliegt sie unweigerlich aus dem System heraus und beschleunigt dabei.

Moment mal, was hast du gerade mit der Gleichung gemacht?

Als ich zunächst feststellte, dass meine Berechnungen völlig gegen den Earnshaw-Satz verstießen, stellte ich fest, dass ich irgendwo einen Fehler gemacht hatte. Es ist am einfachsten, meine Schritte von Anfang an zu verfolgen. Ich holte tief Luft und las über Maxwells Gleichungen . Wieder war ich in der Schule nicht so gut: nicht in den Noten (diese waren ausgezeichnet), sondern in der Menge an Wissen, die ich weggenommen habe. Zum Beispiel habe ich die Maxwell-Gleichungen sofort vergessen, da ich an der Universität und darüber hinaus nicht mit ihnen arbeiten musste.

Es stellt sich heraus, dass sie recht einfach sind, besonders wenn wir nur über elektrostatische Gesetze sprechen! Es gibt vier Maxwell-Gleichungen, eine für jedes dieser Gesetze:

• Das Gauß-Gesetz brauchen wir später. Kurz gesagt, es ist ein Naturschutzgesetz: Energie kann nicht aus dem Nichts erzeugt oder zerstört werden.
• Das Gaußsche Gesetz für Magnetfelder, das im Wesentlichen dasselbe ist. Und wir gehen noch nicht in Magnetfelder, da wir nur über geladene Teilchen sprechen. Überspringe dieses Gesetz.
• Das Faradaysche Gesetz: Bewegliche Magnete erzeugen ein elektrisches Feld. Das ist interessant, wir werden es uns später ansehen.
• Das Ampere-Gesetz: Das Bewegen eines elektrischen Feldes erzeugt ein Magnetfeld. Für unsere Zwecke nutzlos.

Diese vier Gesetze binden also zwei Vektoren E und B, elektrische und magnetische Felder. Diese Vektoren sind Funktionen mit vier Argumenten (x, y, z, t), und jedes der vier Argumente wird einem dreidimensionalen Vektor gegenübergestellt. Wir interessieren uns nicht so sehr für Magnetfelder, also schauen wir uns die elektrischen Felder oder E (x, y, z, t) an. Vergessen Sie nicht, dass wir uns im elektrostatischen Bereich befinden, sodass E über die Zeit konstant ist. Sie können sich diesen Vektor als einen Fluss vorstellen, in dem wir an jedem Punkt sagen, wo und wie schnell das Wasser fließt.

Das Faradaysche Gesetz besagt, dass ein zeitkonstantes E-Feld (wir sprechen dort von Elektrostatik) keine Kräuselung aufweist .

Wie ist das elektrostatische Potential mit elektrischen Feldern verbunden? Einfach: Wenn das E-Feld keine Locken aufweist (wie es dort der Fall ist), können wir u auf eine Weise erzeugen, die (zurück zum Flussbeispiel) von einer 1-Meter-Wasserschicht (in allen Höhen) bedeckt ist! ) und „Loslassen: Geschwindigkeit, Richtung und Richtung des Wasserflusses würden das E-Feld erzeugen. Oder mathematisch gesehen ist es möglich, eine skalare u-Funktion zu finden, deren Gradient dem E-Feld entspricht.

Das Gaußsche Gesetz besagt: Nehmen Sie eine kleine Nachbarschaft. Wenn wir nicht absichtlich Ladungen hineingelegt haben, entspricht die Menge an „Wasser“, die in die Nachbarschaft fließt, der Menge, die herausfließt. Wenn wir klug klingen wollen, ist die Divergenz des E-Feldes Null.

Denken Sie daran: Das E-Feld ist eine Ableitung der Skalarfunktion u. Wenn seine Divergenz Null ist, bedeutet dies, dass der Laplace-Wert von u Null ist. Laplace ist ein kluges Wort für die „Krümmung“ der Funktion. Wenn es sich um Funktionen mit einer Variablen handelt, ist der Laplace-Wert einfach die zweite Ableitung. Bei Funktionen mit zwei Variablen ist der Laplace-Wert die Summe zweier Ableitungen. Wenn es gleich Null ist, sollte die Krümmung in einer Richtung durch die Krümmung in der anderen Richtung aufgehoben werden. Das heißt, Chips können existieren:



Die Null-Laplace-Funktion hat jedoch keine lokalen Minima (oder Maxima), was bedeutet, dass Chips erlaubt sind, die Hügel jedoch nicht:



Stellen Sie sich vor, Sie tauchen einen (gekrümmten) Drahtkreis in Seifenwasser. Der Seifenfilm bildet dann eine Null-Laplace-Oberfläche:



Es wird die sogenannte "minimale Oberfläche" sein. Der Seifenfilm versucht so klein wie möglich zu sein, daher ist es logisch, dass wir bei einem bestimmten lokalen Maximum einen kleineren Film haben würden, indem wir ihn glätten, sodass es keinen gibt. Das elektrostatische Potential ist also eine Art Minimalfläche, die keine lokalen Maxima aufweist (solange wir dort nicht absichtlich Ladungen platziert haben).

Die 1 / r-Funktion hat einen Null-Laplace-Wert in drei Dimensionen, aber nicht in zwei! Wenn wir zweidimensionale Beispiele zeichnen wollen, müssten wir ein Dirichlet-Problem lösen - für 2D ist es -ln r.

Die Verwendung der Formel für inverse Quadrate im 1- oder 2-dimensionalen Raum entspricht einer anderen Einschränkung der Ladungsbewegung entlang der verbleibenden Achsen. In diesem Fall ist es offensichtlich, dass es möglich ist, eine stabile Konfiguration vorzunehmen - nehmen Sie einfach ein Pappröhrchen, stellen Sie es vertikal auf und legen Sie den Magneten ab. Dann ist es möglich, dort einen weiteren Magneten zu platzieren, der im Gleichgewicht ist - horizontal wird er durch das Rohr begrenzt (dh im eindimensionalen Raum), und bei vertikaler Schwerkraft und Abstoßung eines Magneten werden sie ausgeglichen. Der Satz von Earnshaw muss entweder mit dem Gesetz der inversen Quadrate angewendet werden - aber in 3d oder im Raum einer beliebigen Dimension, aber mit dem entsprechenden Potential. "Entsprechend" bedeutet diejenige, die aus Maxwells Gleichungen erhalten wird.

Earnshaws Theorem und seine Konsequenzen

Kommen wir also mit einem frei geladenen Teilchen zu unserem Beispiel zurück. Das Potential eines elektrostatischen Feldes hat keine lokalen Minima und folglich hat die potentielle Energie des Partikels keine lokalen Minima. Ein Teilchen kann also in einem statischen Feld kein stabiles Gleichgewicht erreichen. Herzlichen Glückwunsch, wir haben gerade den Earnshaw-Satz bewiesen. Aber wie wäre es mit komplizierteren Systemen? Wie wende ich den Satz dort an?

Hier ist ein weiteres Beispiel, das laut meinem Chef das Earnshaw-Theorem hätte widerlegen sollen. Lassen Sie uns zwei Ladungen reparieren und einen sich bewegenden Körper erstellen, der aus einem schwerelosen, nicht dehnbaren Stock mit Ladungen an beiden Enden besteht:



Wenn wir den Stick intuitiv leicht nach links oder rechts bewegen, nähert sich eines der Enden den festen Ladungen, wodurch er weggeschoben und der Stick wieder in die ursprüngliche Position gebracht wird. Also, was ist der Haken? Zeichnen wir eine Karte des elektrostatischen Potentials zweier fester Ladungen:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

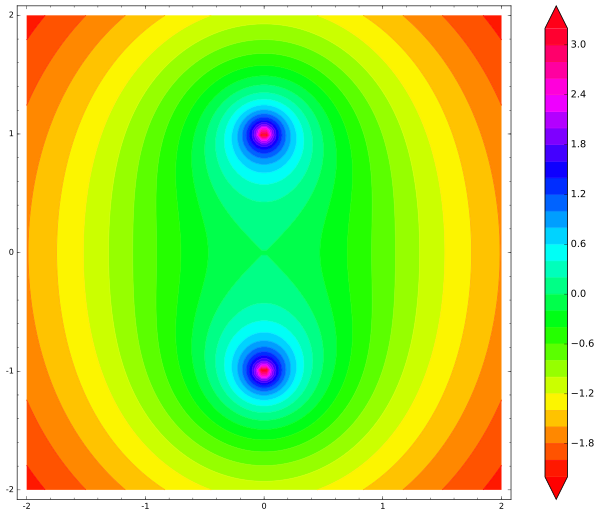
Wie veranschaulichen wir die potenzielle Energie unseres Stocks? Der Stick hat drei Freiheitsgrade (zwei für Bewegung und einer für Rotation), sodass der Graph vierdimensional wäre. Lassen Sie uns die Rotation vorerst ignorieren und den Stick nur hin und her bewegen. Wir fixieren einen Punkt auf einem Stock (zum Beispiel seine Mitte) und zeichnen die Karte der potentiellen Energie des Stocks für seine Mitte. In diesem Fall ist die gesamte potentielle Energie des Sticks die Summe der potentiellen Energien seiner Ladungen an beiden Enden:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y) contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

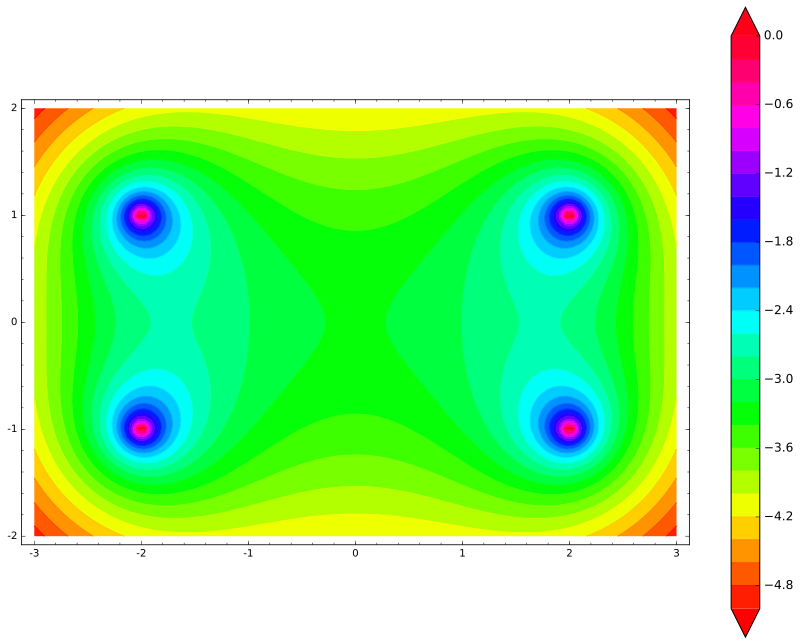
Die Energie des Schlägers hat also vier Spitzen (jedes Ende kann jede der beiden Ladungen treffen). Wie erwartet würde sich der Stick nicht horizontal bewegen - stattdessen würde er sich vertikal bewegen!

Es ist nur logisch, seit wie haben wir die Energie bekommen? Wir haben die potentiellen Energien jeder Ladung addiert. Wir wissen, dass die potentielle Energie jeder Ladung eine Null-Laplace-Funktion ist. Seine Summe hat daher auch einen Null-Laplace-Wert. Daher kann die potentielle Energie eines geladenen Körpers (nicht nur unseres Sticks!) In einem statischen elektrischen Feld kein Minimum haben!

Fazit

Intuitive Bilder von magnetischen und elektrischen Feldern von Menschen, die in der Physik nicht eng zusammenarbeiten, können irreführend sein. Unser Gehirn täuscht uns, indem es Bilder von Energieminima macht. Leider ist dies nicht der Fall, und die Herstellung eines Mendocino-Motors ohne mechanische Unterstützung ist sehr schwierig, wenn nicht unmöglich.

Welche Lücken gibt es zu nutzen? Der Satz von Earnshaw (wenn wir ihn auf Magnete anwenden) gilt nur für Systeme fester, statischer Magnete .

1. Wir können ein dynamisches Magnetfeld erzeugen.
2. Diamagnetismus und Supraleiter fallen ebenfalls nicht unter den Satz von Earnshaw.
3. Bewegliche (und insbesondere rotierende) Körper werden dort überhaupt nicht diskutiert, wobei das Levitron das bekannteste Beispiel ist.

Nein, es ist nicht hoffnungslos. Sicher, die Verwendung einer dieser Lücken würde die Ästhetik eines Mendocino-Motors zerstören, aber die Magie eines frei schwebenden Metall-Dings würde all das übertreffen!

Letzte Anmerkung: Es war der Satz von Earnshaw, der die Nichtexistenz fester Materie bewies und damit das akzeptierte Modell eines Atoms widerlegte, was zum „planetaren“ Atommodell führte.