Wenn Schwarz nach den Standardregeln von Gomoku spielt, benötigt es nicht mehr als
35 Züge, um zu gewinnen. Der Artikel präsentiert Ihrer Aufmerksamkeit eine vollständige Gewinnstrategie und den entsprechenden Algorithmus des Spiels.
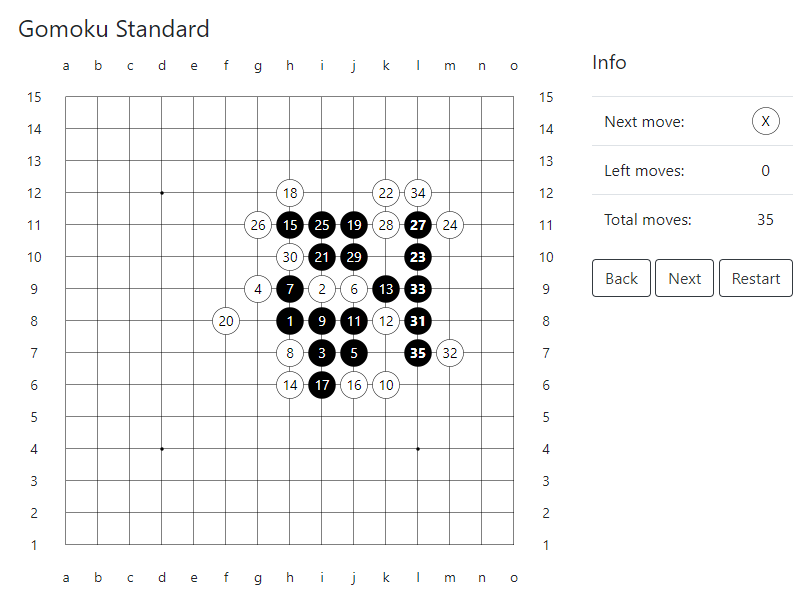
Demonstration der vollständigen Lösung -
hier können Sie spielen und die längsten Optionen finden. Das Programm gewinnt immer und gibt nicht mehr als 35 Züge dafür aus. Der Quellcode der Anwendung, die Lösung selbst und Beispiele von Parteien am Ende des Artikels.
Ich werde nicht auf die Regeln und Taktiken des Spiels eingehen. Das Thema wurde
hier ausführlich auf habr sowie
hier und
hier auf Entscheidungsalgorithmen eingegangen.
Kleiner Exkurs
Vor der Ära der Smartphones war Tic-Tac-Toe „fünf in einer Reihe“ (Gomoku, Renju) einer der beliebtesten Mörder der Zeit im Schulunterricht. Kombinationen zu berücksichtigen war interessanter als die Entwicklung der nordafrikanischen Volkswirtschaft oder die Klassifizierung von Kleeblumen.
Im Herbst 1985 wurden Mädchen aus unserer 10. Klasse aus einer Matheklasse genommen. Wir, die verbleibenden sechs Kinder, hatten höchstwahrscheinlich eine informelle Kommunikation mit einem Mathematiklehrer über abstrakte Themen. Der Lehrer betrat schweigend das Klassenzimmer, verteilte Flugblätter an alle in einer Schachtel und begann, die Namen der Anwesenden an die Tafel zu schreiben. Wir waren depressiv, selbständig oder es war eine Blitzumfrage geplant. Aber die Liste auf dem Brett wurde zu einer Rangliste und wir wurden über die Regeln der Meisterschaft informiert. Jeweils mit jeder Serie von fünf Parteien. Preis an den Gewinner - fünf an das Magazin. Nach den Ergebnissen des Turniers hatte ich das Glück zu gewinnen, aber das Spiel endete nicht dort. Der Lehrer versprach, allen Jungs fünf zu geben, wenn der Gewinner alle fünf Spiele der Serie hintereinander gewinnt. Das Recht des ersten Zuges wird dem Gewinner eingeräumt. Entgegen der Behauptung unseres Lehrers, dass man unter solchen Bedingungen mit dem richtigen Spiel 10, 100 oder eine beliebige Anzahl von Spielen hintereinander gewinnen kann, schien mir der Sieg ein unglaubliches Glück zu sein.
Neun Jahre später, 1994, gab Dr. Lewis Victor Allis in einem Artikel von
Go-Moku und Threat-Space Search Hinweise auf diese Hypothese. Der Autor hat seine Gewinnstrategie nicht veröffentlicht, wodurch er den Beweis überprüfen kann. In seinem 1996 erschienenen Buch
Searching for Solutions in Games and Artificial Intelligence wurde jedoch eine allgemeine Beschreibung der Algorithmen gegeben. Abschließend erwähnen wir separat das Verfahren zur Überprüfung der Vollständigkeit einer Gewinnstrategie, das auf der Richtigkeit der Implementierung des Suchalgorithmus für die "Sequenz von Bedrohungen" und der Analyse der Gegenspieloptionen des Gegners beruht.
Die im Artikel und im Buch angegebenen Lösungsbeispiele mit den „richtigen Zügen“ der Gegner, die Teil einer Gewinnstrategie sind, zeigen die Schwäche des verwendeten Algorithmus.

Zum Beispiel in der Abbildung die Programmlösung für die Standard-Gomoku-Regeln. Wenn Schwarz mit j10 und dann mit j8 als Antwort auf den 10. Zug g9 von Weiß antwortet, endet das Spiel mit 29 statt 45. Zügen. Dann hat das Programm die Kombination der „Bedrohungssequenz“ von Schwarz in 17 Zügen nach dem 16. und nach 26 Zügen zweimal „nicht bemerkt“. Weiß bewegt sich. Und am Ende, wenn Weiß den 36. Zug f12 anstelle von j12 macht, wird er mindestens bis zum 49. Zug durchhalten. Fairerweise muss gesagt werden, dass in diesem Beispiel alle Züge von Schwarz Weiß keine Chance lassen, das Spiel zu seinen Gunsten zu beenden.
Im Internet fand ich mehrere Hinweise auf ähnliche Arbeiten, die nach einer erfolgreichen Strategie suchten. Die Frage nach der Optimalität der gefundenen Lösungen bleibt ungelöst. Was ist die Mindestanzahl an Zügen, die Schwarz benötigt, um zu gewinnen?
Nachdem er 33 Jahre nach der denkwürdigen Schulmeisterschaft ein wenig Freizeit, moderne Computerressourcen und die Hobbys der Kinder gewürdigt hatte, stellte er sich die Aufgabe, die optimale Gewinnstrategie für Schwarz in Gomoku zu finden.
Digitalisieren Sie die Position auf der Tafel
Das Aufnehmen eines Teils ist ziemlich primitiv. Es gibt nur 225 Zellen auf dem Feld. Dementsprechend wird jede Zelle mit 1 Byte codiert. Um einen Stapel von 35 Zügen aufzuzeichnen, sind nur 35 Bytes erforderlich. Eine solche Aufzeichnung ist jedoch aus zwei Gründen für die Positionsbewertung schlecht geeignet: Dieselbe Position kann in einer anderen Abfolge von Bewegungen erhalten werden, und symmetrische Positionen werden nicht berücksichtigt.
Das Erreichen des Ziels des Spiels - fünf Steine hintereinander zu bauen - kann in einer von vier Richtungen ausgeführt werden: vertikal, horizontal und zwei Diagonalen. Somit können wir jede Position als eine Reihe von Linien darstellen. Horizontale und vertikale Linien mit einer Länge von 15 Zellen und diagonale Linien mit einer Länge von 1 bis 15 Zellen. Jede Bewegung ändert den Wert von 4 Zeilen gleichzeitig in verschiedene Richtungen.
Die Aufgabe der Bewertung einer Position besteht darin, alle signifikanten Zahlen für jede Linie zu bestimmen. Der Einfachheit halber beschreiben wir jede Zelle der Leitung mit 2 Bits. Das erste Bit ist voll, wenn ein weißer Stein installiert ist, das zweite Bit ist ein schwarzer Stein. Jede Zeile enthält nicht mehr als 15 Zellen und ist in eine 32-Bit-Ganzzahl codiert. Somit wird die Suche nach Formen auf einer Linie darauf reduziert, den numerischen Wert der Linie durch ein Schiebefenster mit dem Bitmuster der Form zu vergleichen.

In dem in der Abbildung gezeigten Beispiel wird die Position durch 26 Zeilen beschrieben. Dementsprechend wird es mit 104 Bytes codiert, während ein regulärer Batch-Datensatz nur 17 Bytes benötigt.
Es ist leicht zu erraten, dass alle Symmetrien - Drehungen und Spiegelbilder - durch einfaches Ändern der Anzahl (Mischen) und der Richtung der Linien erhalten werden. Um eine Position zu identifizieren und Sammlungen schnell zu durchsuchen, implementiert dieses Prinzip eine 32-Bit-Hash-Funktion, die nur für asymmetrische Positionen unterschiedliche Werte liefert.
Die Verwendung von Symmetrien reduziert die Anzahl der berücksichtigten Positionen erheblich. Beispielsweise wird die Anzahl der Optionen für den zweiten Zug von 224 auf 35 reduziert.
Bei der Suche nach Lösungen und Kombinationen (dies wird unten erläutert) bilden die berechneten Positionen die Eckpunkte des Mehrschichtdiagramms. Die Eckpunkte werden entsprechend der Anzahl der gefüllten Zellen in Schichten gruppiert. Die Bewegungen bilden die Kanten des Diagramms und verbinden die Eckpunkte benachbarter Ebenen. Wenn erfolglose Verschiebungen während der Suche verworfen werden, werden die Kanten gelöscht und einige der Scheitelpunkte verlieren ihre Verbindung zum Hauptzweig. Daher wird nach den Berechnungsschritten die Speicherbereinigung (oder die Neuerstellung des Diagramms von oben) durchgeführt.
Während des Entwicklungsprozesses wurden mehrere Codierungsalgorithmen berücksichtigt, aber der oben beschriebene zeigte die höchste Rate der Positionsschätzung.
Position bewerten
Ein wichtiger Faktor für die Bewertung einer Position ist, wie wichtig die Gegner die signifikanten Teile gebaut haben.
Fünf - wenn solch ein Stück auf dem Brett gefunden wird, ist das Spiel vorbei. Für Standardregeln, keine Sechser, Siebener usw., geben Sie Gomoku einen Preis. Daher erfordern die fünf, wie übrigens alle anderen Figuren, das Fehlen ihrer Steine auf benachbarten Zellen in einer Linie.
 Die offenen vier
Die offenen vier - die Länge von 6 Zellen, die mittleren vier sind von gleichfarbigen Steinen besetzt, die äußeren sind notwendigerweise leer. Nun, bei fünf fehlen ihre Steine in benachbarten Zellen. Eine sehr starke Figur bedeutet, auch bei einem anderen Zug zu gewinnen.
 Vier
Vier - die Länge von 5 Zellen, eine (beliebige) der fünf Zellen ist frei. Gibt einen Gewinn für sich. Es schafft eine Bedrohung und zwingt den Gegner, sich in einer freien Zelle zu bewegen, wenn er seine vier nicht hat. Gibt 5 Punkte in der Bewertung der Position während der Verteidigung.

 Ein offenes Tripel
Ein offenes Tripel - die Länge von 6 oder 7 Zellen, die äußersten Zellen sind notwendigerweise frei. Bei 6 Zellen sind drei der vier mittleren mit Steinen gleicher Farbe besetzt, einer frei. Für 7 Zellen - drei mittlere sind mit gleichfarbigen Steinen besetzt. Eine Figur wiederum wird zu einer offenen Vier, wenn der Gegner keine Vier oder eine offene Drei hat. Wenn jemand anderes sich bewegt, entsteht eine Bedrohung und der Gegner wird gezwungen, die drei zu schließen oder seine vier als Antwort zu setzen. Das Triple der 6. Zelle hat 1 Hebe- und 3 Schließbewegungen. Das Triple der 7. Zelle hat 2 Erhöhungsbewegungen und nur 2 Schließbewegungen. Gibt 2 bis 4 Punkte in der Positionsbewertung.


 Ein Tripel
Ein Tripel oder ein geschlossenes Tripel ist eine Länge von 5 Zellen, von denen drei von Steinen derselben Farbe besetzt sind. Die drei an ihrem Zug können in eine vier verwandelt werden und werden für Angriff und Verteidigung verwendet, wodurch eine Bedrohung entsteht, die mehr als eine offene Drei des Gegners ist. Gibt 1 Punkt in der Positionsbewertung.


 Eine offene
Eine offene (perspektivische)
Zwei - 6 bis 7 Zellen lang. Beim Angriff wird es in eine offene Drei umgewandelt. Gibt 1 oder 2 Punkte in der Positionsbewertung.


 Ein Plug
Ein Plug ist gleichzeitig zwei oder mehr Bedrohungen, die nicht auf einmal geschlossen werden können. Es gibt 3x3 Gabeln (zwei offene Dreifachgabeln), 3x4 Gabeln (offene Dreier und Vierer) und 4x4 Gabeln (zwei offene Vierer). Gabeln geben einen Gewinn, wenn der Gegner keine größere Bedrohung hat - eine Vier oder eine offene Drei für eine 3x3 Gabel oder der Gegner kann die Gabel nicht nacheinander schließen. große Bedrohungen schaffen - eine Folge von Vieren für eine 3x3-Gabel.



 Kombination
Kombination - eine kontinuierliche Abfolge von Bedrohungen und Abwehrmechanismen gegen größere Bedrohungen des Gegners, die zu einem positiven Ergebnis für den Spieler führen. Kombinationen greifen an (oder gewinnen) und sind defensiv.
Die Angriffs- oder Gewinnkombination ist erfolgreich, wenn bei Verteidigungs- oder Angriffsbewegungen des Gegners Antwortbewegungen gefunden wurden, die zu einem Sieg führten. Die Angriffskombination endet mit der Installation eines Steckers, den der Gegner nicht schließen kann.
Die Verteidigungskombination ist im Gegenteil erfolgreich, wenn der Gegner keine Bedrohungen mehr erzeugt oder die Grenze der zu berechnenden Züge überschritten wird. Eine Verteidigungskombination besteht aus Verteidigungsbewegungen oder einer größeren Bedrohung für den Gegner.
Bei der Bewertung einer Position wird nach einer Gewinnkombination gesucht. Bei Erfolg haben wir gewonnen. Andernfalls ist der Staat neutral, wenn keine Bedrohung durch den Gegner vorliegt. Wenn der Gegner droht, suchen wir nach einer defensiven Kombination. Wenn erfolgreich, ist der Staat neutral, wenn er versagt, verlieren wir.
Da die Anzahl der Optionen für Angriffe und erzwungene Vergeltungsmaßnahmen sehr begrenzt ist, ist es zulässig, nach Kombinationen mit einer ausreichend großen Tiefe zu suchen. Während der anfänglichen Konstruktion der optimalen Strategie wurde die zulässige Tiefe der Suche nach Kombinationen über 25 Züge festgelegt. Bei der Neuberechnung der Lösung zur Implementierung des Positionsschätzungsalgorithmus in Javascript wurde die zulässige Suchtiefe auf 17 Züge reduziert.
Bei der Berechnung der optimalen Strategie wurde die Suchtiefe der Gewinnkombination von oben zusätzlich durch die maximale Zielanzahl von Zügen begrenzt.
Wir suchen nach einer Lösung
Also bewerteten wir die angegebene Position als neutral und wählten den nächsten Schritt. Unser Verhalten in diesem Fall hängt davon ab, ob wir die angreifende oder die verteidigende Seite sind. Für die angreifende Seite ist die vollständige Lösung eine Folge von Zügen, bei denen für den Rückzug eines Gegners die Position als gewinnend bewertet wird (eine Gewinnkombination wird gefunden) oder die Lösung den nächsten eigenen Zug enthält. Es ist erwähnenswert, dass zur Berechnung der optimalen Strategie die angreifende Seite immer schwarz und die verteidigende Seite weiß ist.
Die angreifende Seite muss nur einen Zug finden, was zum schnellsten Sieg führt. Unter den Bedingungen eines Mangels an Ressourcen begrenzt der Angreifer die Anzahl der Optionen für das Busting künstlich. Ich untersuche zunächst die Bewegungen, die zu der Position mit der höchsten Bewertungspunktzahl führen. Nachdem Lösungen gefunden wurden, erweitert der Angreifer in Richtung der längsten Lösung den Bereich der Optionen und erkundet Positionen mit weniger Nennwerten, um die Länge der Lösung zu verringern.
Es reicht für die verteidigende Seite aus, einen einzigen Zug zu finden, der nicht zum Sieg des Gegners in der vorgegebenen Anzahl von Zügen führt. Alle freien Zellen können zur Aufzählung verwendet werden.
Um die Anzahl der zu sortierenden Züge zu verringern, verwenden wir den Algorithmus "Überspringen". Wir überspringen die Defensive und suchen nach einer gewinnbringenden Angriffskombination. Bei Erfolg können mögliche Verteidigungsbewegungen auf Bewegungen beschränkt sein, die den Erfolg der gefundenen Kombination beeinflussen. Im Durchschnitt können Sie bei jedem Schritt den Suchbereich um das 4-6-fache reduzieren. Bitte beachten Sie, dass es unter den ignorierten Zügen möglicherweise längere Zweige der Lösung gibt. Um nach optimalen Lösungen zu suchen, wird der "Überspringen" -Algorithmus daher nur bei der anfänglichen Suche verwendet.
Wir berechnen die Strategie
Alle Komponenten sind fertig, wir legen den ersten schwarzen Stein in die Mitte des Feldes, starten die Suche nach einer Lösung und ... Nach einigen Stunden gehen die Ressourcen meines Laptops zur Neige und ich muss zugeben, dass ich "im Kampf, aber nicht im Kampf" geschlagen habe.
In Wahrheit hatte ich Rechenleistung mit anderthalbhundert Kernen Xeon und einem Terabyte freiem RAM zur Hand. Denken Sie jedoch daran, dass Allis Mitte der neunziger Jahre nur 10 SUN SPARCstation 2 auf jeweils 128 MB RAM hatte, Reue für unsportliches Verhalten empfand und beschloss, die RAM-Menge auf dem Java-Computer auf 1 GB zu beschränken und nur 1 Thread für die Aufgabe zuzuweisen der Prozessor. Es könnte irgendwie mein GHz im Vergleich zu seinem MHz kompensieren. Außerdem versprach er sich am Ende der Arbeit, die Algorithmen für den Browser auf Javascript zu übertragen.
Die Suche nach Strategien musste also mit der Entscheidung der Debütskizzen beginnen. Eine ausführliche Beschreibung der Debüts für das Renju-Spiel in russischer Sprache finden Sie in Sagars berühmten Büchern "From Debut to Middlegame" und Mikhail Kozhin und Alexander Nosovskys "Ringing of the Stones"
hier . Die Bücher sind bereits 20 Jahre alt, aber seitdem wurde ein wenig solche Literatur veröffentlicht. Die neuere Sammlung von Dmitry Epifanov „Tiger in a cage“ von 2015 ist leider nicht in elektronischer Form erhältlich.
Die Suche nach optimalen Öffnungsentscheidungen wurde nach dem folgenden Algorithmus durchgeführt. Im ersten Schritt wurde eine vorläufige Berechnung durchgeführt, ohne die Länge der Charge zu begrenzen. Dann wurde für die längsten Lösungen eine Optimierung durchgeführt: Ersetzen der gefundenen Kombinationen durch kürzere Lösungen für die letzten Schritte und Suchen nach kürzeren Entscheidungszweigen für alle Zwischenbewegungen. Die Optimierung wurde durchgeführt, bis die Zielgrenze für alle Zweige der Lösung erreicht war. Dann verringerte sich das Ziellimit und es wurde versucht, auf einen neuen Wert zu optimieren.


Beim dritten vertikalen Debüt in Abbildung 3 gab es keine Probleme. Das Ergebnis war ein vollständiger Satz von Lösungen. Die schwierigsten Positionen nach dem 4. Zug i8 und j10 wurden in 31 Zügen gelöst. Dann wurde ein Ziellimit von 35 Zügen pro Spiel festgelegt.


Aus der Diagonale für die Entscheidung wählte er traditionell das 7. Debüt. Die schwierigste Position ergibt sich nach dem 4. Zug g9. Zulässige Längenlösungen wurden für 6 Züge g8 und g7 gefunden.

Aber für diese Option konnte ich mit dem 6. Zug auf j9 keine Lösung finden, die kürzer als 33 Züge war. Es war fast eine Katastrophe. Aus Verzweiflung versuchte ich die Lösungen für den alternativen 5. Zug sowie alle anderen Arten von diagonalen Öffnungen. Die Debüts wurden bis zum Ende gelöst, aber es konnten keine kürzeren als 39 Züge pro Spiel gefunden werden.
Zurück zum ursprünglichen Debüt in der 7. Diagonale überarbeitete er den Algorithmus zum Generieren von Sätzen für Angriffszüge. Infolgedessen führten Bewegungen, die zu Positionen mit einer Bewertung von den dritten zehn führten, unerwartet zu einem Ergebnis und reduzierten die Länge des Lösungspfads. Die Variabilität der Berechnung mit einem solchen Betrag wurde ziemlich groß. Bei einer Lösungstiefe von 12 Zügen gab es mehr als 2 Millionen Positionen (ohne Positionen bei der Suche nach Kombinationen). Die Fortsetzung beruhte auf 1 GB RAM, das für die Aufgabe zugewiesen wurde. Um die Entscheidung bis zur letzten Gabelung zu überprüfen, war es in einigen Fällen erforderlich, die Positionen ab dem 18. Zug separat zu bestimmen.
Nachdem das Debüt in der 7. Diagonale in 35 Zügen entschieden war, konnte man den Sieg feiern - der Kampf um das Zentrum war gewonnen. Vor uns lag noch eine enorme Menge an routinemäßiger Rechenarbeit, Berechnungen von „nicht optimalen“ weißen Bewegungen, um die Strategie zu vervollständigen. Vom Gesamtvolumen der optimalen Strategie betrug die Antwort auf solche Bewegungen 80%. Glücklicherweise wurden sie nach dem zweiten Zug nach vorläufiger Berechnung automatisch vollständig gelöst, und all dieses Volumen wurde innerhalb weniger Tage zur optimalen Strategie hinzugefügt.
So wurden Lösungen für alle 2 Züge gefunden. Wir legen den ersten schwarzen Stein in die Mitte des Feldes, beginnen mit der Suche nach einer Lösung und haben nicht einmal Zeit, die Wichtigkeit des Augenblicks zu spüren - die Ausgangsposition wurde in 35 Zügen gelöst. Das Diagramm der optimalen Gewinnstrategie wird erstellt.
Überprüfen Sie uns
Der nächste Schritt ist die Überprüfung der Lösung. Schalten Sie die Intelligenz der verteidigenden Seite vollständig aus. Nach jeder Bewegung von Schwarz geht Weiß zu einem beliebigen freien Feld des Bretts. Die Position, die nach dem Zug von Weiß erhalten wurde, muss entweder im Entscheidungsdiagramm gefunden oder als Gewinn für die Anzahl der Züge bewertet werden, die den längsten Zweig in der Startposition nicht überschreiten. Bei der Bewertung jeder Position überprüfen wir die gefundene Gewinnkombination für alle zulässigen Züge von Weiß, bevor Schwarz das letzte Stück baut - fünf in Folge.
Die Prüfung wurde bis zum Abschluss mehrmals durchgeführt. Der letzte fehlerfreie Lauf im Single-Threaded-Modus dauerte 14 Stunden. Im Verlauf der Überprüfung wurden Fehler gefunden und korrigiert, die sich aus Unterschieden in der Suchtiefe nach Kombinationen, Annahmen zum Überspringen und Duplizieren symmetrischer Positionen ergaben.
Beantworten Sie die Frage - ist die Entscheidung in 35 Zügen wirklich die optimalste? Nach meinen Recherchen ist es für eine Reihe der längsten Zweige des vertikalen Debüts möglich, mit einer Länge von 33 Zügen optimalere Lösungen zu finden. Aber für die Diagonale nach dem 6. Zug auf j9 wurde viel Zeit aufgewendet, um in 33 Zügen nach einer Lösung zu suchen. Die Variation für Schwarz wurde bei jedem Schritt auf 50 Züge erweitert, ohne Erfolg. Es ist nicht möglich, das Fehlen einer Lösung in 33 Zügen rigoros nachzuweisen, die für das Projekt vorgesehene Zeit ist abgelaufen und es wurde beschlossen, bei der Zielgrenze von 35 Zügen anzuhalten.
Konvertieren Sie von Java nach Javascript
Die Veröffentlichung einer Lösung für ein Problem erfordert Klarheit.
Um die Lösung direkt im Browser verwenden zu können, war Folgendes erforderlich:- Reduzieren Sie die Tiefe der Suche nach Kombinationen bei der Bewertung von Positionen auf 17 Züge. Dies führte zu einer 2-3-fachen Erhöhung der Anzahl der berechneten Züge der optimalen Strategie.
- Konvertieren Sie das binäre Entscheidungsdiagrammformat in eine JSON-Bewegungssequenz. Dieses Format ist in Javascript und visuell bequemer.
- Konvertieren Sie Java-Klassen in Javascript-Module, mit Ausnahme von Entscheidungsverfahren. Ersetzen Sie hier in der Weboberfläche die Rest-Service-Aufrufe durch lokale Funktionen.
Liste der Anwendungsklassen:- Board - Party Management auf dem Board, visuelle Schnittstelle
- Scheitelpunkt - oben im Entscheidungsdiagramm, von der Position geerbt
- Kante - Kante des Entscheidungsgraphen, Verbindungspositionen verschieben
- Layout - Position, enthält eine Sammlung von Linien
- Linie - Eine Linie in einer bestimmten Richtung enthält eine Sammlung von Formen
- Abbildung - Eine Abbildung, die den Typ und den Beginn einer Abbildung in einer Linie bestimmt
- Muster - Muster von Zahlen zum Vergleich bei der Suche
Die vollständige Lösung im JSON-Format kann aus der Datei gomoku.json heruntergeladen werden .Quellen im Repository auf GitHub .Zur Verdeutlichung werde ich im Folgenden Beispiele für die längsten Spiele geben, die in der Demonstration erhalten wurden, indem Sie auf Weiter klicken.Diagonales Debüt:
 Vertikales Debüt:
Vertikales Debüt:
