Leseschwierigkeiten
Einführung und Spielregeln
Vor ein paar Jahren habe ich das Spiel Dobble gekauft ( Dobble , der ursprüngliche Name ist "Spot It!"). Dies ist ein sehr einfaches, schnelles und unterhaltsames Spiel, das ich als eines der besten Brettspiele überhaupt betrachte.
Das Spiel enthält 55 Karten mit jeweils 8 verschiedenen Symbolen. So sehen diese Karten aus:

Abb. 1. Ein Beispiel für eine Spielkarte.
Auf jeweils zwei Karten stimmt ein und nur ein Symbol überein. In der obigen Abbildung ist dies ein Stiftsymbol:

Abb. 2. Übereinstimmende Zeichen auf Karten.
Der Spieler, der das Spiel zum ersten Mal gesehen hat, führt je nach Spielrunde eine Aktion auf einer der Karten aus. Nimmt es zum Beispiel für sich selbst oder wirft es einem Gegner zu.
Oft führt dies dazu, dass sich eine der Karten, für die Spieler nach Spielen suchen, ändert. Aus diesem Grund müssen Sie nach einer neuen Übereinstimmung suchen, die ein völlig anderes Symbol sein kann:


Abb. 3, 4. Die erste Karte wird durch eine neue ersetzt. Jetzt gibt es einen neuen Zufall zwischen ihnen - das Symbol des Clowns.
Wie machen sie das?
Auf den ersten Blick scheint es unglaublich, dass auf zwei Karten genau ein Zufall, nicht mehr und nicht weniger. Die Fragen stellen sich sofort - wie viele Charaktere gibt es im Spiel? Sie können nicht zu wenige (dann gibt es mehr als eine Übereinstimmung auf den Karten) oder zu viel (dann dürfen keine Übereinstimmungen auf den Karten vorhanden sein) sein.
Darüber hinaus ist es offensichtlich, dass sich die Symbole in einer speziellen Reihenfolge auf den Karten befinden, was die einzige Übereinstimmung für zwei beliebige Karten garantiert.
Die Grundkenntnisse von Google führen uns zur Stackoverflow-Website, auf der beschrieben wird, warum dies geschieht: http://stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game
Das Spiel verwendet die Prinzipien der endlichen Geometrie . Obwohl dieses Wort das Wort „Geometrie“ enthält, bezieht sich dieses Konzept mehr auf Kombinatorik als auf Geometrie. Es arbeitet mit einer endlichen Anzahl von Punkten, die insbesondere in Form einer Projektionsebene lokalisiert werden können.
Karten und Symbole im Spiel sind Elemente der Projektionsebene 7. Ordnung. Dies bedeutet, dass auf jeder Karte n + 1 Symbol vorhanden ist und die Gesamtzahl der eindeutigen Symbole im Spiel n ^ 2 + n + 1 beträgt, d. H. 57 Zeichen.
Es gibt Flugzeuge niedriger und höherer Ordnung. Zum Beispiel gibt es eine Ebene 5. Ordnung. Für sie werden 6 Symbole auf der Karte angezeigt, und die Gesamtzahl der eindeutigen Symbole im Spiel beträgt 5 ^ 2 + 5 + 1 = 31. Die Projektionsebene dieser Konfiguration wird in einer einfacheren Version des Spiels Doble namens "Doble 1,2,3" verwendet .
Die Verbindung zwischen Punkten und Linien für die Projektionsebene wird mithilfe der Inzidenzmatrix festgelegt . Sein Aussehen wird im Abschnitt „Inzidenzmatrix für das Spiel Dobble“ vorgestellt.
Endgültige Geometrie für Babys
Viel später als beim Schreiben des Originalartikels besuchte ich einen Vortrag von Alexei Savvateev , in dem er über projektive Geometrie sprach, die viel kürzer und verständlicher war. Da ich aus diesem Grund nicht die Kraft oder den Wunsch habe, die Hälfte des Artikels neu zu schreiben, empfehle ich nur sein Buch "Mathematik für die Geisteswissenschaften", wenn mein Versuch des Wilden, das Gerät des Autos an den Fingern zu erklären, unverständlich oder langweilig wäre.
Gehen Sie zuerst zu Wikipedia und lesen Sie einige Artikel. Der erste Artikel beschreibt das Konzept der endlichen Geometrie:
Eine endliche Geometrie ist ein beliebiges geometrisches System mit einer endlichen Anzahl von Punkten . [1]
Bisher ist alles einfach. Wenn Sie mehrere Punkte mit einem Stift auf Papier zeichnen, bilden sie bereits eine endliche Geometrie.
Eine Überraschung erwartet viele weitere:
Zum Beispiel ist die euklidische Geometrie nicht endlich, da die euklidische Linie eine unbegrenzte Anzahl von Punkten enthält oder vielmehr genau so viele Punkte enthält, wie es reelle Zahlen gibt . [1]
Für uns bedeutet dies, dass das Stück Papier, auf dem unsere Punkte gezeichnet sind, keine Ebene in Bezug auf die endliche Geometrie ist . Es ist nur ein Punktträger.
In der Ebene gibt es zwei Arten von Geometrie: affine und projektive . In der affinen Geometrie wird der übliche Begriff der Parallelität von Linien verwendet. [1]
Erinnern Sie sich daran, welche Axiome die affine Geometrie beschreiben:
Die affine Geometrie in einer Ebene ist eine nicht leere Menge X (deren Elemente als "Punkte" bezeichnet werden) mit einer nicht leeren Sammlung von L Teilmengen von X (deren Elemente als "direkt" bezeichnet werden), so dass:
- Für zwei verschiedene Punkte gibt es nur eine Linie, die beide Punkte enthält.
- Für eine Linie ℓ und einen Punkt p, der nicht zu ℓ gehört , existiert eine und nur eine Linie ℓ ', die p enthält, so dass ℓ ∩ ℓ ′ = ∅ ist.
- Es gibt viele von vier Punkten, von denen keiner auf derselben Linie liegt. [1]
Diese Axiome geben uns die Möglichkeit zu verstehen, wie die einfachste affine Ebene in endlicher Geometrie aussieht:
Die einfachste affine Ebene enthält nur 4 Punkte und wird als affine Ebene zweiter Ordnung bezeichnet . Jedes Punktpaar definiert eine eindeutige Linie, daher enthält die angegebene Ebene 6 Linien. [1]
Nicht sehr klar? Alles ist richtig. Wenn Sie sich die Definition der affinen Geometrie genau ansehen, können Sie sehen, dass sie mit den Konzepten der Mengenlehre (Element, Menge, Teilmenge) arbeitet.
Dies bedeutet, dass die Linien möglicherweise überhaupt nicht wie die üblichen Linien der euklidischen Geometrie aussehen.
In der Tat ist es. Wenn Sie sich das Bild der affinen Ebene zweiter Ordnung ansehen, sehen Sie das folgende Bild:

Abb. 5. Athener Ebene zweiter Ordnung. (Quelle ru.wikipedia.org )
Die Punkte hier sehen aus wie gewöhnliche schwarze Punkte, aber die geraden Linien sind mehrfarbige Segmente. Linien derselben Farbe werden als parallel betrachtet.
Wie Sie sehen können, sind die Linien hier nicht unendlich lang. Im Geheimen werde ich sagen, dass es hier überhaupt kein Konzept der Länge gibt und gerade Linien jede Form haben können, wie wir bald sehen werden.
Sicherlich bezweifelt% username% immer noch, dass das Bild dieser Ebene die Axiome der affinen Geometrie erfüllt. Lassen Sie uns überprüfen:
- Wir nehmen 2 beliebige Punkte, zum Beispiel oben links und unten links.
Beide Punkte enthalten nur eine linke rote Linie.
Die rechte rote Linie enthält keinen dieser Punkte, und die verbleibenden Linien enthalten nur einen davon. - Nehmen Sie die linke rote gerade Linie und den rechten oberen Punkt. Offensichtlich ist nur eine gerade Linie (rechts rot) parallel zur linken roten Linie, da sie durch den oberen rechten Punkt verläuft, aber keinen der beiden linken Punkte durchläuft.
- Die Abbildung zeigt deutlich, dass unabhängig davon, welche 3 Punkte wir nehmen, einer von ihnen auf einer Linie liegt, die sich von der Linie unterscheidet, auf der beide anderen Punkte liegen.
Die beiden Linien, aus denen die Diagonalen eines Quadrats bestehen, schneiden sich nicht, da sie keine gemeinsamen Punkte haben.
Wenn Sie den Inhalt des vorherigen Bildes gut verstanden haben, ist das Bild komplizierter:
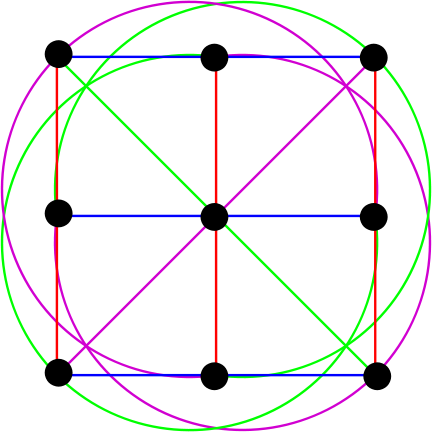
Abb. 6. Athener Ebene dritter Ordnung. (Quelle ru.wikipedia.org )
Hier sehen wir 9 Punkte und 12 Linien. Ja,% Benutzername%, diese Ellipsen sind tatsächlich gerade Linien in Bezug auf die endliche Geometrie.
Formen derselben Farbe sind parallele Linien. Sie sind schwer zu bemerken, deshalb teilen wir das Bild in mehrere:
| Flugzeug Nummer 1 | Flugzeug Nummer 2 | Flugzeug Nummer 3 | Flugzeug Nummer 4 |
|---|
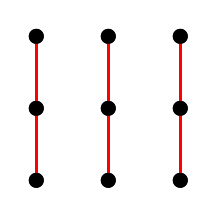 | 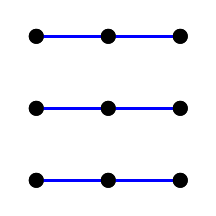 |  |  |
Abb. 7. Parallele gerade Linien der affinen Ebene dritter Ordnung.
Hier dauert die Überprüfung der Ausführung von Axiomen etwas länger:
- Wir nehmen 2 beliebige Punkte, zum Beispiel den mittleren oberen und unteren rechten. Durch sie geht nur eine der lila Linien.
- Nehmen Sie die linke rote Linie und den unteren rechten Punkt. Ähnlich wie bei einer Ebene zweiter Ordnung verläuft nur eine rechte rote Linie durch diesen Punkt, jedoch nicht durch einen der drei linken Punkte.
- Hier ist es etwas komplizierter als bei einem Flugzeug 2. Ordnung. Die Aussage des Axioms besagt, dass Sie mindestens eine (nicht leere) Menge von vier Punkten finden müssen, in denen keine drei auf mehr als einer Linie liegen.
Offensichtlich erfüllen 12 Sätze mit drei Punkten, durch die die Linien in der Figur verlaufen, diese Bedingung nicht. Aber es erfüllt zum Beispiel einen Satz von vier Eckpunkten.
In einem allgemeineren Fall hat eine endliche affine Ebene der Ordnung n n ^ 2 Punkte und n ^ 2 + n Linien; Jede Linie enthält n Punkte und jeder Punkt gehört zu n + 1 Linien. [1]
Wenn die affine Geometrie fertig ist, gehen wir zum zweiten Geometrietyp in der Ebene über - projektiv.
In der projektiven Geometrie hingegen schneiden sich zwei beliebige Linien am einzig möglichen Punkt, und daher existieren keine parallelen Linien. [1]
Der vorige Satz beschreibt das zweite Axiom der projektiven Geometrie. Der erste und der dritte sind die gleichen wie beim Athener.
Da das dritte Axiom die Existenz von mindestens vier Punkten erfordert, muss die Ebene mindestens 7 Punkte enthalten, um die Bedingungen der ersten beiden Axiome zu erfüllen. In dieser einfachsten der projektiven Ebenen gibt es auch 7 Linien; Jeder Punkt gehört zu drei Linien, und jede Linie enthält drei Punkte. Eine solche projektive Ebene wird oft als "Fano-Ebene" bezeichnet. [1]
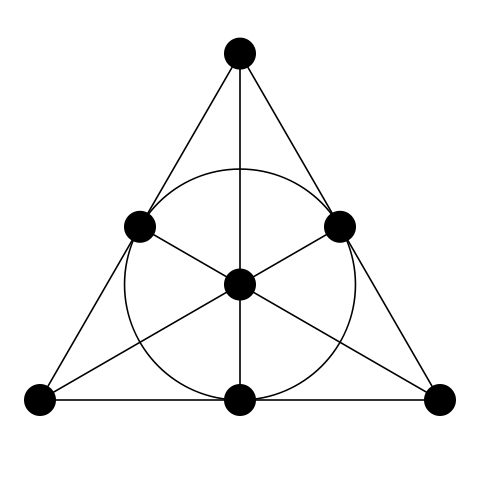
Abb. 8. Fano Flugzeug. (Quelle en.wikipedia.org )
In dieser Abbildung ist es schwierig, alle 7 Zeilen sofort zu verstehen. Hier ist eine Pony-Version derselben Ebene:
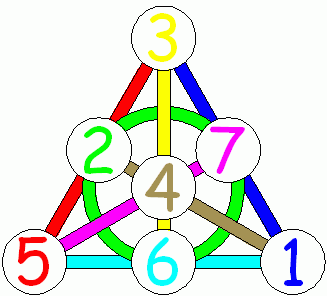
Abb. 9. Fano-Ebene mit farbigen Linien. (Quelle mathpuzzle.com . Verwendung mit Genehmigung von Ed Pegg Jr. )
Die Fano-Ebene ist also eine projektive Ebene 2 Ordnung mit 7 Punkten und 7 Linien.
Was hat die Karte damit zu tun?
Was passiert, wenn wir zwei Axiome endlicher Geometrie neu formulieren und die „Linie“ durch das „Symbol“ und den „Punkt“ durch die „Karte“ ersetzen?
Das Ergebnis ist folgendes:
- Für zwei verschiedene Karten gibt es nur ein Symbol, das auf beiden Karten angezeigt wird.
- Für zwei verschiedene Symbole gibt es nur eine Karte, die beide Symbole enthält.
Lassen Sie uns nun anhand dieses Wissens sehen, wie Dobble im einfachsten Fall aussehen würde. Es hätte 7 Karten und 7 Zeichen, jede Karte hätte 3 Zeichen (da sich 3 Linien an einem Punkt schneiden):
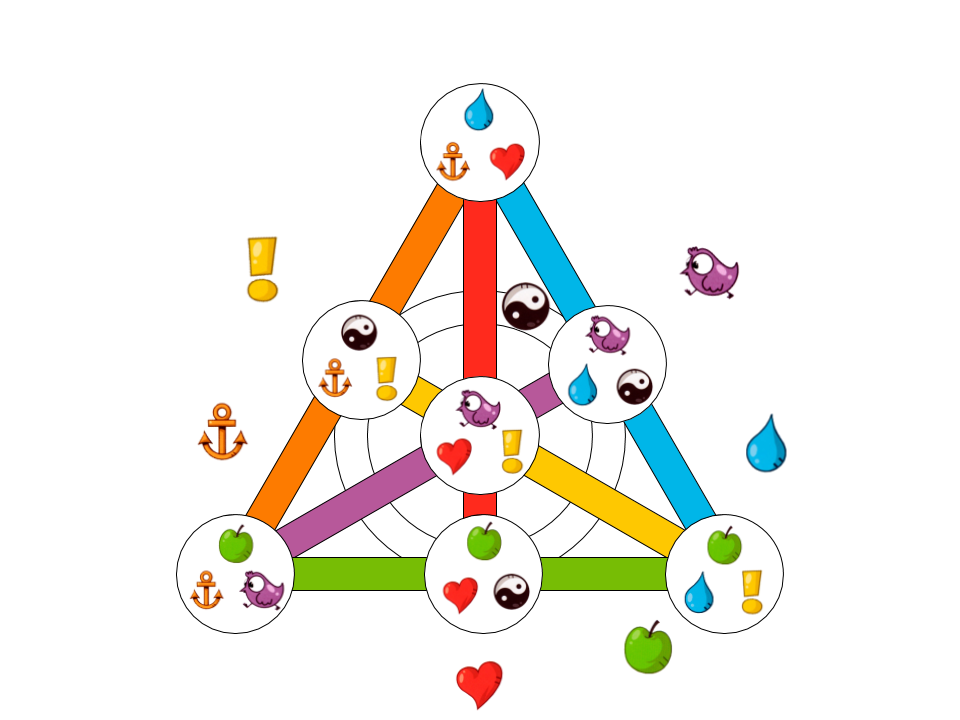
Abb. 10. Ein Beispiel für den kleinstmöglichen Kartensatz für Dobble.
Die folgenden 7 Zeichen werden hier verwendet:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Unabhängig davon, welche 2 Karten wir nehmen, haben sie ein gemeinsames Symbol neben der Linie, auf der beide Karten liegen.
Beispielsweise haben die Karte in der unteren linken Ecke und die Karte in der Mitte der rechten Seite ein gemeinsames Symbol  . Es wird neben der Zeile angezeigt.
. Es wird neben der Zeile angezeigt.  .
.
Projektive Flugzeuge kleiner Aufträge
Auf Wolfram finden Sie eine visuelle Demonstration von Projektionsebenen kleiner Aufträge: http://demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
Es ist als Dokument im CDF-Format (Computable Document Format) konzipiert, für das Sie den CDF-Player installieren müssen.
Hier ist ein Beispiel einer projektiven Ebene der Ordnung 3:
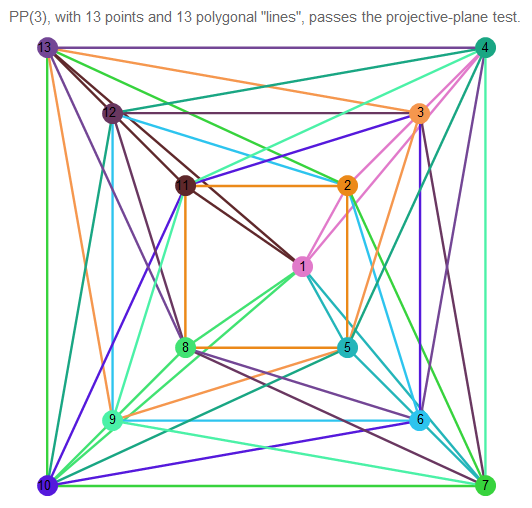
Abb. 11. Bild der Projektionsebene von 3 Ordnungen.
Es ist schwer zu verstehen, was passiert. Nehmen Sie also zwei beliebige Zeilen:
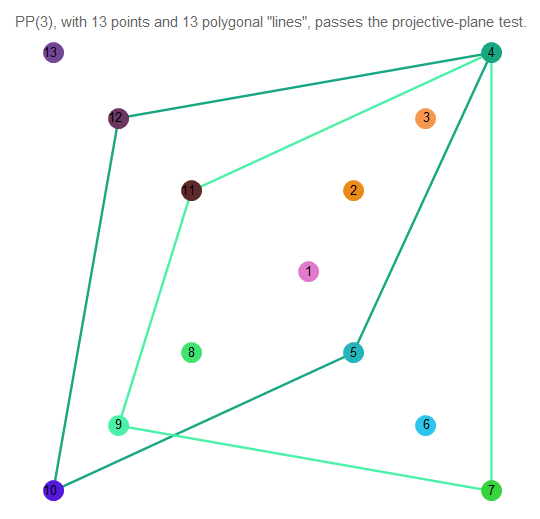
Abb. 12. Der Schnittpunkt zweier Linien der Projektionsebene 3. Ordnung.
Wie wir sehen, schneiden sie sich genau an einem Punkt. Die Linien selbst enthalten 4 Punkte.
Um sicherzustellen, dass 4 Linien durch jeden Punkt verlaufen, müssen Sie die angezeigten Linienpaare in einem interaktiven Dokument wechseln und sich auf einen bestimmten Punkt konzentrieren.
Projektive Ebenen höherer Ordnung sind in den folgenden Abbildungen dargestellt.
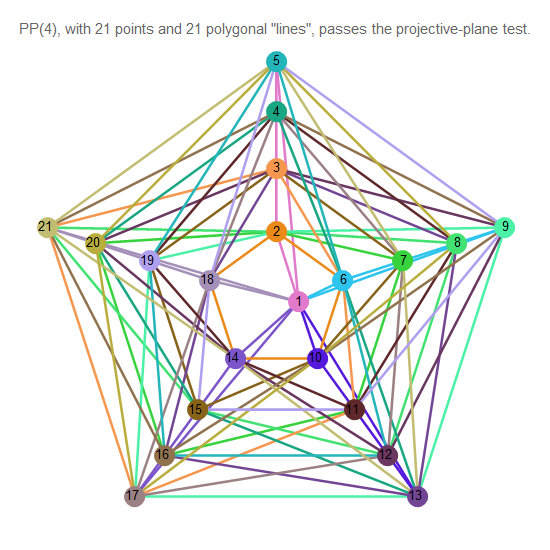
Abb. 13. Projektive Ebene der Ordnung 4
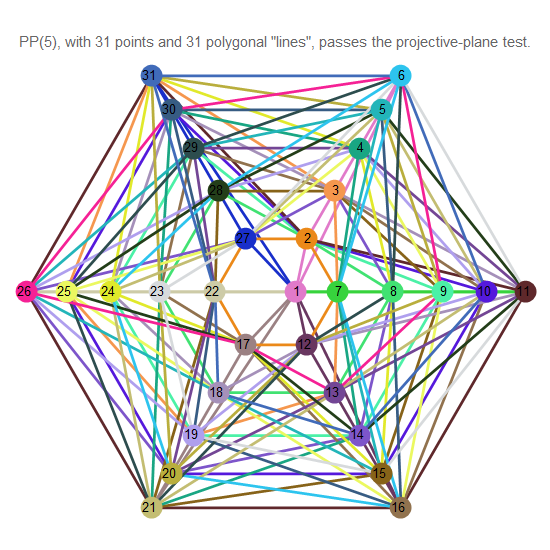
Abb. 14. Die projektive Ebene der Ordnung 5

Abb. 15. Projektive Ebene der Ordnung 7
In der obigen Sequenz gibt es kein Bild für die Projektionsebene 6. Ordnung. Dies ist kein Fehler.
Obwohl Wolfram eine grafische Darstellung einer solchen Struktur erzeugt, erfüllt es nicht die Axiome der projektiven Geometrie und ist keine projektive Ebene.
Es wird angenommen, aber immer noch nicht bewiesen, dass die Ordnung einer endlichen Ebene immer eine Primzahl ist . [1]
Wie baue ich eine projektive Ebene?
Die grafische Darstellung der projektiven Ebene sieht interessant und klar aus, aber wie kann man eine solche Kombination von Punkten finden, damit sie die oben genannten Eigenschaften besitzt?
Am einfachsten ist es, Websites zu besuchen, auf denen vorberechnete Daten für Projektionsebenen verschiedener Größenordnungen gespeichert sind.
Für die projektive Ebene der Ordnung 7 können Sie beispielsweise die folgende Seite besuchen: https://web.archive.org/web/20170619110638/https://www.uwyo.edu/moorhouse/pub/planes/pg27.txt
Dort wird eine Zahlenmatrix dargestellt. Linien sind Karten (Punkte) in Bezug auf Dobble. Die Zahlen in den Zeilen sind die Seriennummern der Zeichen (Zeilen) ab Null, die auf jeder Karte gezeichnet sind (durch diesen Punkt gehen).
Sie können auch die Dienste mathematischer Pakete wie Matlab verwenden, um die Inzidenzmatrix der Projektionsebene zu erstellen. [2] [3]
Inzidenzmatrizen
Die Inzidenzmatrix ist eine der Diagrammdarstellungen , die die Beziehungen zwischen den einfallenden Elementen des Diagramms (Kante (Bogen) und Scheitelpunkt) angibt. Die Spalten der Matrix entsprechen Kanten, die Zeilen Scheitelpunkten. Ein Wert ungleich Null in der Matrixzelle gibt die Beziehung zwischen dem Scheitelpunkt und der Kante (deren Häufigkeit ) an. [2]
Eines der einfachsten Beispiele für die Inzidenzmatrix kann eine 2x1-Matrix für einen ungerichteten Graphen von zwei Scheitelpunkten sein, die durch eine Kante verbunden sind:

Abb. 16. Ein ungerichteter Graph von zwei durch eine Kante verbundenen Eckpunkten und deren Einfallsmatrix.
Ein komplexeres Beispiel für ein Diagramm und seine Inzidenzmatrix:
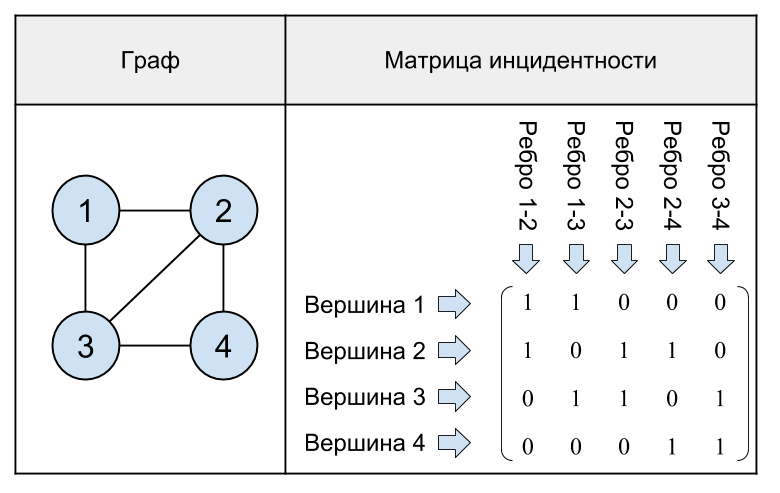
Abb. 17. Ein ungerichteter Graph mit 4 Eckpunkten und seiner Inzidenzmatrix.
Wie aus dem letzten Beispiel ersichtlich ist, gibt es in der Inzidenzmatrix des Diagramms in jeder Spalte genau zwei Einheiten, weil Eine Kante verbindet zwei Eckpunkte.
Die projektive Ebene ist ein Hypergraph , da eine Linie (Kante) mehrere Punkte (Eckpunkte) verbindet. Daher treten in der Inzidenzmatrix der Projektionsebene Einheiten in jeder Spalte n + 1 Mal auf, wobei n die Reihenfolge der Projektionsebene ist.
Für die in Abb. In 9 ist die Inzidenzmatrix wie folgt:

Abb. 18. Die Inzidenzmatrix der Fano-Ebene.
Um die Wahrnehmung zu vereinfachen, werden Nullen nicht angezeigt und Einheiten werden durch das Symbol X ersetzt.
In dieser Darstellung der Projektionsebene ist das Dualitätsprinzip von Punkten und Linien deutlich sichtbar - die Linie verläuft durch genau 3 Punkte und gleichzeitig gehört der Punkt zu genau drei Linien.
Mit roher Gewalt eine projektive Ebene bauen
Das aktuelle Wissen über die Eigenschaften der Inzidenzmatrix reicht aus, um sie für die Projektionsebene beliebiger Ordnung n zu konstruieren. Dazu können Sie den folgenden Pseudocode verwenden:
n+1 , n+1 , ,
Nach diesem Algorithmus erhalten wir eine symmetrische Matrix für die Fano-Ebene:

Abb. 19. Die durch den Pseudocode-Algorithmus konstruierte Fano-Ebenen-Inzidenzmatrix.
Diese Matrix stimmt nicht mit der vorherigen überein. Tatsächlich spielt es keine Rolle.
Die Permutation von zwei beliebigen Zeilen der Inzidenzmatrix entspricht der Umnummerierung der Scheitelpunkte des Diagramms.
Die Permutation von zwei beliebigen Spalten der Inzidenzmatrix entspricht der Umnummerierung der Kanten des Diagramms (sofern diese im Voraus nummeriert sind).
Incident Matrix für Dobble
Für das Spiel Dobble in der Inzidenzmatrix sind die Zeilen für die Karten und die Spalten für die Zeichen auf ihnen verantwortlich.
Somit entspricht die Permutation von zwei beliebigen Spalten der Inzidenzmatrix einer Änderung der Zeichenfolge auf der Karte. Die Symbole auf der Karte sind jedoch ungeordnet, sodass dieser Vorgang das Erscheinungsbild der Karten nicht beeinträchtigt.
Durch die Neuanordnung von zwei Zeilen ersetzen sich auf allen Karten zwei entsprechende Symbole.
Die letzte Operation ändert das Aussehen der Karten, was bedeutet, dass der Zeichensatz, den wir im Spiel sehen, nur eine der möglichen Kombinationen ist.
Die Anzahl der Zeichensätze für eine bestimmte Karte ist eine Kombination aus 57 Elementen und 8 Elementen ohne Wiederholung. Es wird nach der Formel berechnet 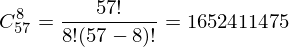
Die Inzidenzmatrix für Dobble ist in der folgenden Tabelle aufgeführt. Es wird transponiert, d.h. Zeilen sind Symbole und Spalten sind Karten (das Bild ist anklickbar). In Habr können Sie kein Bild mit der gewünschten Größe und Qualität einfügen. Daher ist die Option in voller Größe ein separater Link: https://github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble%20incidence%20matrix.png

Abb. 20. Die Inzidenzmatrix des Spiels Dobble.
Welche zwei Karten fehlen im Spiel?
Insgesamt enthält die Tabelle mit der Inzidenzmatrix des Spiels 57 Zeilen und 55 Spalten. Dies bedeutet, dass das Spiel 2 weitere Karten haben könnte.
Dies bedeutet, dass die Charaktere, die auf diesen Karten sein sollten, im Spiel weniger häufig sind als die anderen. Die Anzahl der Charaktere im Spiel wird in der letzten Spalte der Tabelle angezeigt.
Die Anzahl der Zeichen auf den fehlenden Karten ist wie folgt:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  und
und 
(Insgesamt 14 Zeichen) kommen 7 Mal vor. kommt 6 mal vor.
kommt 6 mal vor.
Wie sehen die fehlenden Karten aus? Um diese Frage zu beantworten, nehmen Sie eines der oben genannten Zeichen in die Inzidenzmatrix (mit Ausnahme des Schneemanns) und platzieren Sie es auf der fehlenden Karte (z. B. der vorletzten Spalte).
Dann finden wir alle Karten (Spalten), auf denen dieses Symbol abgebildet ist. Dies bedeutet, dass auf all diesen Karten die Symbole übereinstimmen und es keine anderen Übereinstimmungen geben kann.
Da diese Karten bereits mit dem ausgewählten Charakter übereinstimmen, streichen Sie in der vorletzten Spalte alle Zeichen durch, die auf den anderen Karten erscheinen.
Fehlende Charaktere, die nicht durchgestrichen wurden, bilden die Charaktere einer der verbleibenden Karten. Da sie genau 8 waren, wird der Typ der zweiten fehlenden Karte eindeutig bestimmt.
Hier sind diese 2 Karten:


Abb. 21. Ein möglicher Typ fehlender Karten ist Nr. 56 und Nr. 57.
Es bleibt die letzte Frage zu beantworten: Beeinträchtigt das Fehlen dieser Karten die Eigenschaft des Zusammentreffens eines einzelnen Symbols zwischen zwei Karten (d. H. Plötzlich gibt es keine Übereinstimmungen zwischen Karten)?
Die Antwort liegt auf der Hand, wenn Sie sich immer noch die Inzidenzmatrix des Spiels ansehen - nein, das tut es nicht. Zwischen zwei beliebigen Karten (Spalten) besteht immer noch der einzige Zufall.
Warum gibt es 2 Karten weniger als das maximal mögliche im Spiel?
Anfangs waren die Regeln für die fünf Minispiele nicht in der Broschüre enthalten, sondern auf fünf separaten Karten. Gleichzeitig konnten nur 60 Karten gedruckt werden. Daher haben die Autoren des Spiels beschlossen, 2 Karten zu entfernen, so dass sich am Ende 55 Karten mit Symbolen + 5 Karten mit Regeln herausstellten. (Besonderer Dank geht an Guillaume Gille-Naves für die Klarstellung.)
Danksagung
Ich bedanke mich beim Netzwerk der Brettspieleläden „Igroved“ für die Hilfe beim Schreiben des Artikels.
Vielen Dank an Ed Pegg Jr. für die Bereitstellung des Fano-Flugzeugbildes.
Unabhängig davon möchte ich einen Anonymus und einen Master erwähnen, um Hilfe bei der Überprüfung des Artikels zu erhalten.
Ich danke dem "Table City" -Laden für ihre Hilfe bei der Vorbereitung der Veröffentlichung des Artikels.
Ich danke den Autoren des Spiels Igor Polouchine, Denis Blanchot, Guillaume Gille-Naves und Asmodee von ganzem Herzen für das Recht, Bilder aus dem Spiel zu verwenden.