Ausgeglichenes ternäres
Ich arbeite an Vorlesungen über Computerarchitekturprinzipien für unsere Universität. und als Aufgabe möchte ich meinen Schülern vorschlagen, eine einfache programmierbare Maschine zu bauen, die
ternär arbeitet . Der Hauptgrund macht Spaß: Als Dozent muss ich ein bisschen Unterhaltung mitbringen, sonst werde ich nicht angehört. Außerdem ist es aus historischen Gründen wichtig. Noch ein "Warum ?!" Fragen werden beantwortet "Weil ich kann."
Diese Seite beschreibt die Grundlagen und geht nicht über einen einfachen ternären Addierer (und dessen Hardware-Implementierung) hinaus. Bleib dran für mehr.
Ich habe das ausgeglichene ternäre System gewählt: Jeder Trit repräsentiert einen von drei möglichen Zuständen, -1, 0 oder 1. Eine sehr ausführliche Beschreibung dieses Systems finden Sie
hier .

Der Grundbaustein: ternärer Multiplexer
Abstraktion
Der einzige Block, der in meinem Computer verwendet wird, ist der ternäre Multiplexer.
Es kann als Black Box mit fünf Pins angesehen werden: Der Auswahlstift empfängt ein ternäres Signal (entweder -1, 0 oder 1), und dann befindet sich in der Box ein kleiner Schalter, der den Ausgangsstift mit einem der drei Eingangsstifte verbindet inN, inO oder inP.
Normalerweise wird es wie hier gezeigt dargestellt:
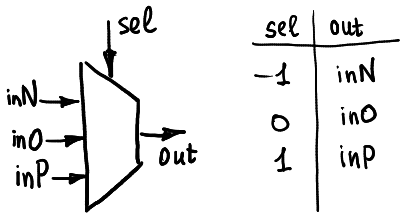
Der ternäre Demultiplexer funktioniert ähnlich: Abhängig vom Auswahlstift ist ein Eingang mit einem von drei möglichen Ausgangspins verbunden. Beachten Sie, dass ich in meiner Hardware analoge CMOS-Switches verwende. Diese sind bidirektional, sodass die Hardware sowohl als Multiplexer als auch als Demultiplexer verwendet werden kann. Aber im Moment benutze ich sowieso keine Demultiplex-Möglichkeiten.
Hardware-Implementierung
Das grundlegende Design wurde von
Shaos vorgeschlagen.
Ich habe nur eine SMD-Version von TRIMUX erstellt. Oberflächenmontierte dg403-Schalter können in China für 50 Pence pro Stück gekauft werden.
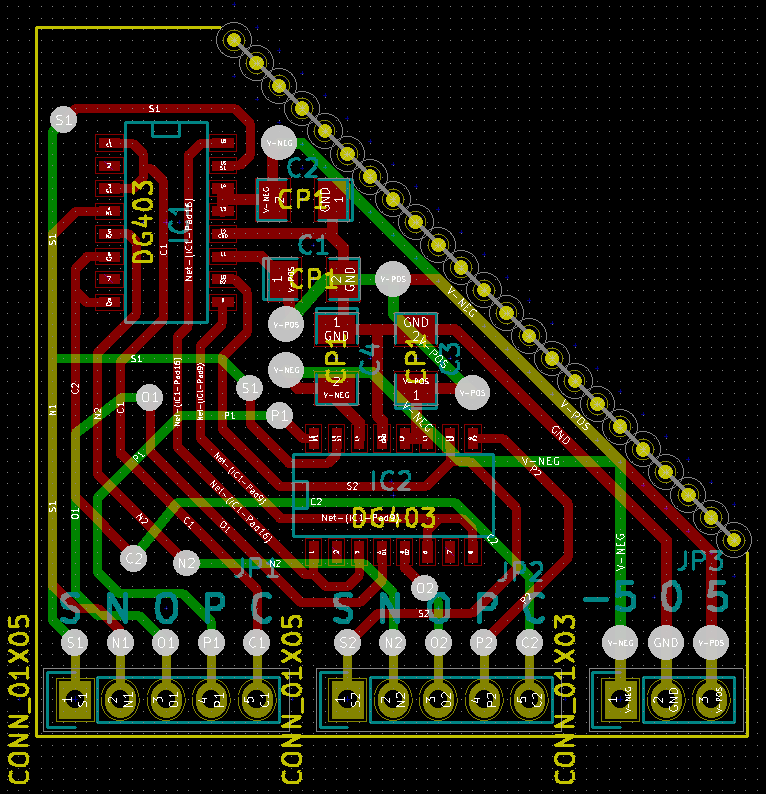
Bevor ich dieses Design fand, habe ich versucht, Kombinationen von cd4007 und cd4016 zu verwenden. Es hat funktioniert, aber die Hardware ist umständlich und hässlich. DG403-Switches bieten echte ternäre Rechenmöglichkeiten ohne Redundanz, z. B. die Verwendung von Zwei-Bit-Binärdateien und das Verbot einer von vier Konfigurationen.
Ein ternärer Multiplexer kann mit zwei DG403 erstellt werden: Einer der ICs empfängt eine Leistungsaufnahme von -5 V bis 0 V, während der andere mit 0 V bis 5 V versorgt wird, und ermöglicht die Verwendung von ternären Signalen, die durch drei Spannungen von -5 V, 0 V und 5 V dargestellt werden. jeweils. Dieses Design verwendet nur die Hälfte der dg403-Pins, daher ist es natürlich, eine Platine mit zwei Multiplexern zu erstellen.
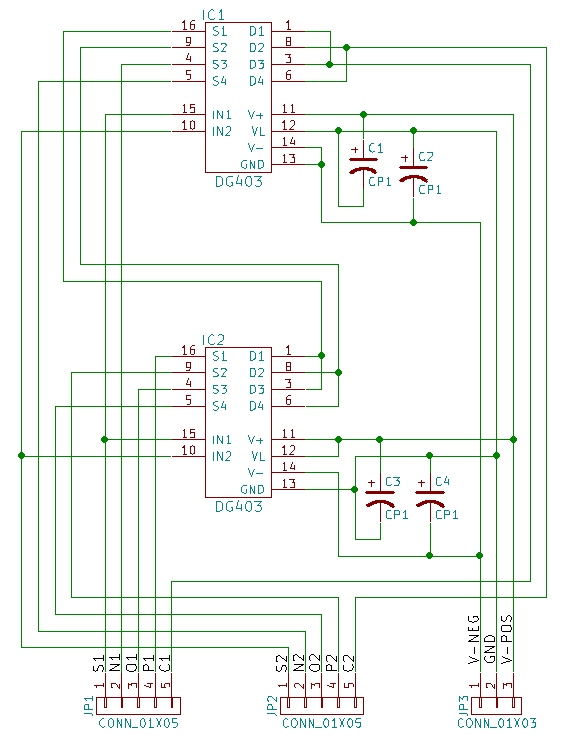
Zögern Sie nicht, Shaos
hier zu kontaktieren. Anstatt über die Vorteile des Ternären zu spekulieren, entwarf und fertigte er seine eigenen ternären ICs!

Wie benutzt man es? Unäre Funktionen
Lassen wir die Identitätsfunktion weg, die wir erhalten können, indem wir den entsprechenden Eingangsstiften des Multiplexers -1,0 und 1 geben.
Für den Anfang erhöhen wir das Eingangssignal A durch Berechnung von A + 1 (natürlich im -1,0,1-Ring):
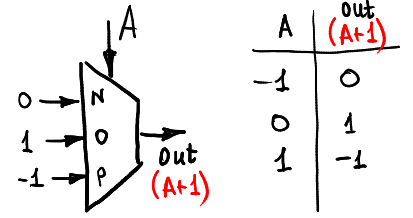
Hier ist die Art und Weise, wie wir die Eingabe dekrementieren können:
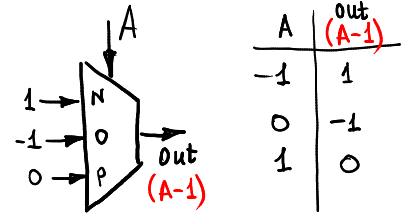
Berechnen wir max (A, 0):
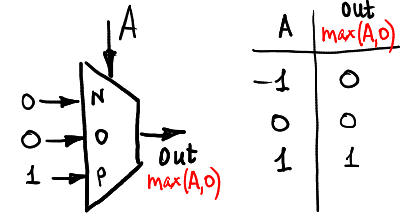
Und die min (A, 0):
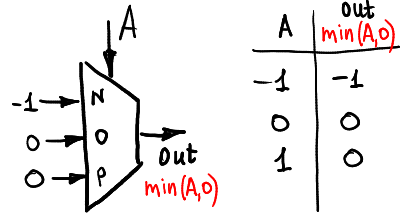
Funktionen von zwei Argumenten: Halbaddierer
A + B.
Ein Multiplexer ermöglicht es uns also, jede unäre Funktion zu berechnen. Um eine Funktion aus zwei Argumenten zu berechnen, müssen drei oder vier Multiplexer verwendet werden. Wenn wir beispielsweise eine Summe von zwei Signalen A und B (noch im Ring -1,0,1) berechnen möchten, können wir dieses Schema verwenden:
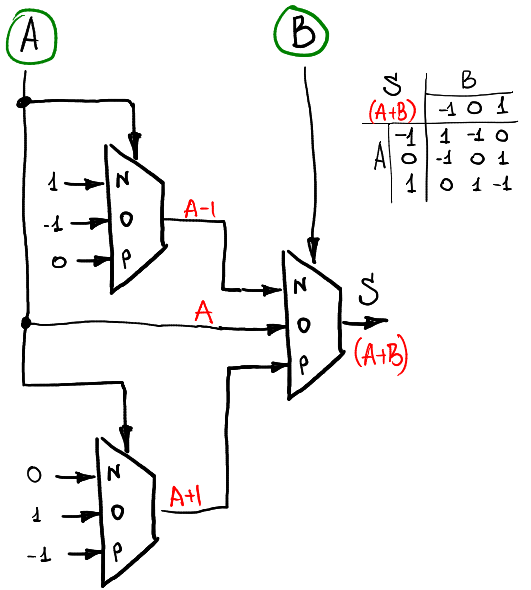
Es gibt zwei Schichten von Multiplexern: Die erste Schicht berechnet unäre Funktionen von A und die zweite Schicht kombiniert sie gemäß B.
Konsens
Wenn wir die Konsensfunktion von zwei ternären Signalen berechnen wollen (Konsens ist gleich -1, wenn A = B = -1, gleich 1, wenn A = B = 1 und sonst Null), dann können wir das so machen:
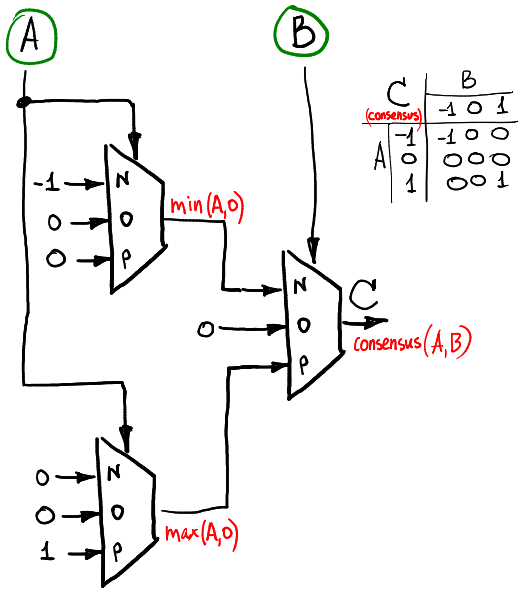
Hardware-Implementierung
Tatsächlich haben wir gerade
einen Halbaddierer erstellt . Für zwei Eingänge A und B werden zwei Ausgänge S und C berechnet, die sich auf A + B = S + 3 * C beziehen. S ist die Summe und C ist das Übertragsflag.
Lassen Sie uns das Design testen! Rote LED bedeutet -1, Aus bedeutet 0, grüne LED bedeutet 1. Auf diesem Foto sehen wir also, dass S = -1, C = 1 oder mit anderen Worten 1 + 1 = -1 + 3 * 1:

Hier ist die Tabelle, in der alle neun möglichen Zustände unseres Halbaddierers aufgeführt sind. Jede Zelle gibt entsprechende Werte für S und C an. Für jede Zelle wird ein Link zu einem Foto bereitgestellt.
Drei Argumente: Volladdierer
Im Gegensatz zum
Halbaddierer empfängt
ein Volladdierer drei Eingänge A, B, Cin und berechnet zwei Ausgänge S und Cout, die als A + B + Cin = S + 3 * Cout zusammenhängen.
Summe von drei Triten
Wenn wir eine Summe von A + B + Cin berechnen möchten, ist die Idee dieselbe wie zuvor: Wir verwenden die schichtweise Vorbereitung von Eingaben. Die erste Schicht empfängt A als Eingabe, die zweite verwendet B und die letzte Einzelmultiplexerschicht verwendet Cin. Hier ist eine Möglichkeit, die Ausgabe S zu berechnen:
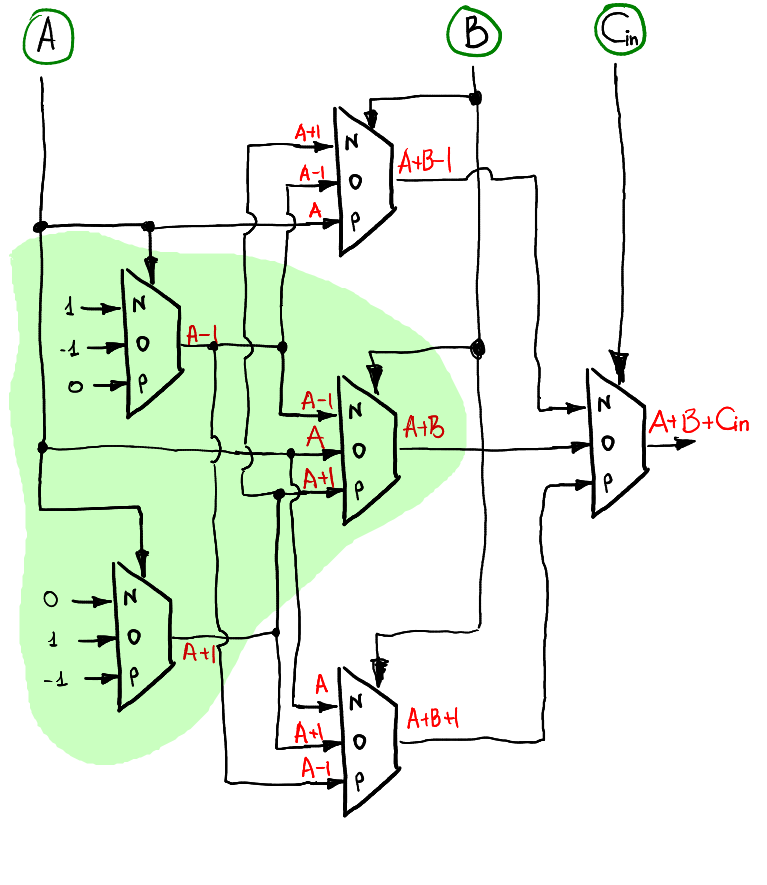
Beachten Sie, dass sich Cin = 0 genau so verhält wie der Halbaddierer. Daher ist es natürlich, dass die Halbaddiererschemata im Volladdierer enthalten sind (grün hervorgehoben).
Überlauf (Carry Flag)
Der Überlauf-Trit kann auf dieselbe schichtweise Weise berechnet werden. Es ist auch der Halbaddierer enthalten!
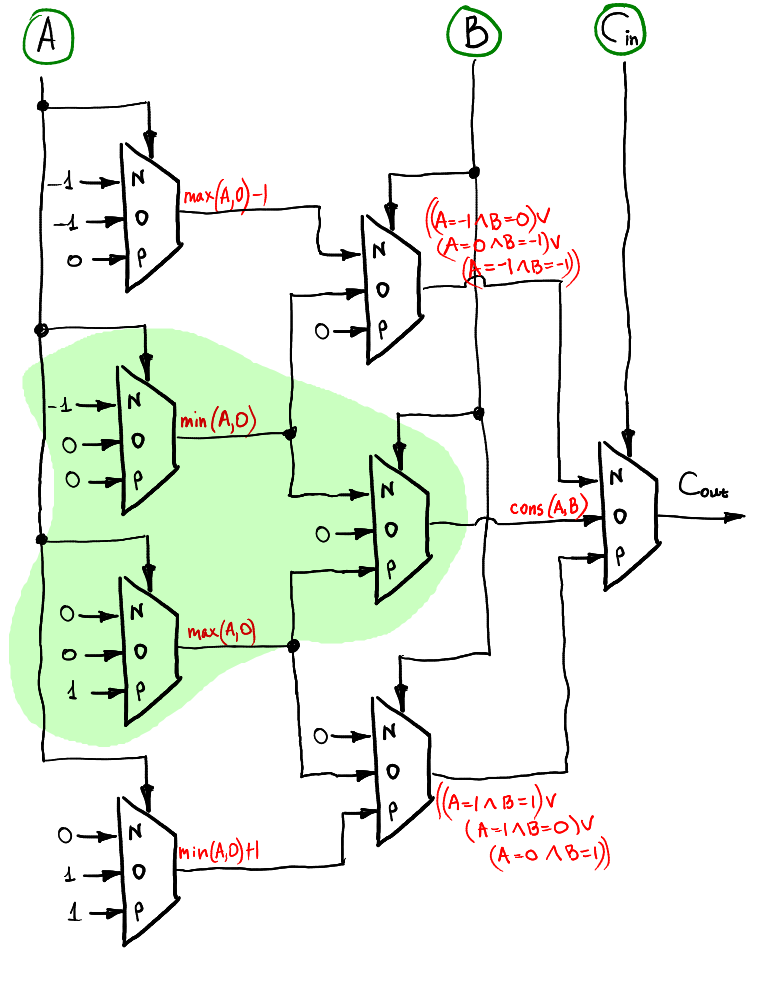
Hardware-Validierung
Dieses Mal war ich zu faul, um den Volladdierer mit Steckbrettern zu testen, also habe ich diese einschichtige Leiterplatte hergestellt:

Hier ist es, nachdem das Kupfer geätzt wurde:

In drei folgenden Tabellen sind alle 27 möglichen Zustände des Volladdierers aufgeführt. Nach wie vor sind die Fotos für jeden Staat verfügbar. Beachten Sie, dass die mittlere Tabelle (Cin = 0) genau die gleiche ist wie für den Halbaddierer.
Der Vorteil des Volladdierers gegenüber dem Halbaddierer ist die Möglichkeit, mehrere Addierer zu stapeln, bis wir genug Trits erhalten, um die gewünschte Zahl darzustellen.
Hier ist ein Stapel von zwei Addierern:

Und hier, wie es -4 + 2 löst (der niedrigstwertige Trit ist links):

Natürlich brauchen wir kein Volladdierer-Board für den niedrigstwertigen Trit (wir haben kein Carry-Flag für die Eingabe des niedrigstwertigen Trits), ein Halbaddierer würde ausreichen.
Fazit
Dies ist das Ende der Einführung in das ternäre Computing. Seien Sie gespannt auf Uhren, Zähler, Speicher und mehr!