💪 ⛄️ 👘 Quantencomputer in Spielen oder ernsthaft verrückt werden 👨🏽‍🚒 🚨 🛕

Wenn Sie unter den Verrückten leben, müssen Sie lernen, selbst verrückt zu sein

Haben Sie jemals versucht, "lernen, verrückt zu sein"? Nicht triviale Aufgabe. Sie werden nicht einmal eine normale Technik finden, weil jeder auf seine Weise verrückt wird. Mein erster Versuch: Verschwörungstheorie. Die Theorie beinhaltet keine Praxis, was bedeutet, dass Sie nicht hart arbeiten müssen. Auch in jeder Situation wird niemand leiden.

Wie erstelle ich Verschwörungstheorien?

Die Erstellung einer Verschwörungstheorie ist relativ einfach. Wir brauchen eine Idee, die einfach genug ist, um von 90% der Bevölkerung akzeptiert zu werden. Es sollte kontrovers sein, damit 5% der Bevölkerung 90% erklären können, was für Idioten sie sind. Schließlich brauchen wir einige Untersuchungen, die diese 95% der Menschen nicht verstehen, die aber von 90% als Argument verwendet werden: "Die Menschen haben sich als schlauer erwiesen als wir ...".

Quantum Computing ist ein großartiger Bereich für eine solche Studie. Sie können ein einfaches Schema zusammenstellen, aber das Wort "Quantum" erhöht das Gewicht der Ergebnisse.

Das Objekt des Studiums ist ein Spiel, denn das Objekt ist auf die einfache und vertraute Jugend zurückzuführen. Wer ist an Quantencomputern und Spielen beteiligt? Google

Also, ketzerische Theorie: Nach 5 Jahren werden Page und Green entscheiden, wer die Hauptsache in Google sein wird, und dies mit Hilfe des Spiels tun. Jeder von ihnen hat eine Gruppe von Forschern. Das AlphaGo-Team mit seinen ~~kämpfenden~~ neuronalen Netzen zog Rivalen in Go an. Die Gegner waren gezwungen, nach neuen Methoden zu suchen, und fanden dennoch ein Instrument der ~~völligen~~ Überlegenheit: das Quantencomputing.

Kann ich Quantum Computing für Spiele verwenden? Einfach. Lassen Sie uns zum Beispiel zeigen, dass das Spiel "Fuchsjäger" in 6 Zügen "gelöst" werden kann. Aus Gründen der Glaubwürdigkeit beschränken wir uns auf 15 Qubits (die Online-Editor-Eigenart emuliert nicht länger als fünfzehn). Der Einfachheit halber werden wir die Einschränkungen der Prozessorarchitektur und der Fehlerkorrektur ignorieren.

Die Regeln

Sehr einfach. Es gibt fünf Löcher in einer Reihe (wir nummerieren sie als 0-1-2-3-4). In einem von ihnen ist ein Fuchs. Jede Nacht bewegt sich der Fuchs zum nächsten Nerz links oder rechts. Jeden Morgen kann der Jäger ein Loch zur Auswahl prüfen. Die Aufgabe des Jägers ist es, den Fuchs zu fangen. Die Aufgabe des Fuchses ist es zu überleben. Theoretisch kann ein Fuchs für immer vor einem Jäger fliehen. In der Praxis gibt es eine Gewinnstrategie: Überprüfen Sie die Löcher 1-2-3-1-2-3. Nur diese Strategie werde ich testen.

Ein Schema aufbauen

Beginnen wir mit der Initiierung der Qubits 0-1-2-3-4 (5 Löcher). Hier können Sie bearbeiten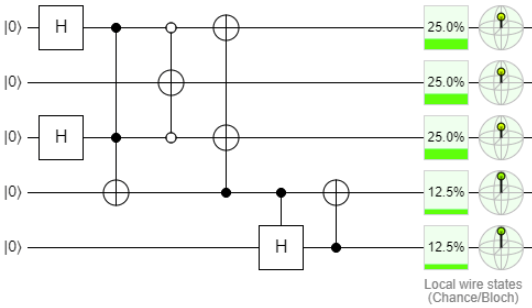

Tatsächlich haben wir nach der Initiierung ein System, in dem nach der Messung streng ein Qubit einzeln ist. Die Wahrscheinlichkeiten der "Einheit" unterscheiden sich für jedes Qubit, aber in unserem Fall ist dies nicht kritisch. Wir müssen Raum für Diskussionen über das Schema (und gleichzeitig unsere Theorie) lassen.

Auf Q # erhalten wir Code wie folgt:

operation TestStrategy () : (Result) { let res = Zero; using(qubits=Qubit[16]) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history InitFoxHoles(qubits); ResetAll(qubits); // ALWAYS clean after yourself } return Zero; } // Inits fox holes, with almost equal probabilities operation InitFoxHoles(register: Qubit[]) : Unit { body { ResetAll(register); // Step 1 H(register[0]); H(register[2]); // Step 2 (Controlled (X))([register[0],register[2]], register[3]); // Step 3 X(register[0]); X(register[2]); (Controlled (X))([register[0],register[2]], register[3]); X(register[0]); X(register[2]); // Step 4 CNOT(register[3], register[0]); CNOT(register[3], register[2]); // Step 5 (Controlled (H))([register[3]], register[4]); // Step 6 CNOT(register[4], register[3]); } }

TestStrategy testet unsere Strategie 1-2-3-1-2-3. InitFoxHoles () ist nur für die Initiierung von Fuchslöchern verantwortlich. Lassen Sie uns die Initiation überprüfen. Kopieren Sie TestStrategy, starten Sie die Initiierung, messen Sie die ersten 5 Qubits und geben Sie ihre Werte zurück.

  operation TestInit(): (Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; using(qubits=Qubit[16]) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history InitFoxHoles(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4); } }

Wir werden den Test tausendmal durchführen (mehrere Läufe sind typisch für Quantenalgorithmen, an einigen Stellen sogar notwendig). Rufcode - unter dem Spoiler, Ergebnisse: auf dem Bildschirm unten.

Testen Sie die Initiierung schnell

  static void TestInitiation() { using (var sim = new QuantumSimulator()) { var initedQubitsValues = Enumerable.Range(0, 5) .ToDictionary(qubitIndex => qubitIndex, oneMesaured => 0); for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result) result = TestInit.Run(sim).Result; if (result.Item1 == Result.One) { initedQubitsValues[0]++; } if (result.Item2 == Result.One) { initedQubitsValues[1]++; } if (result.Item3 == Result.One) { initedQubitsValues[2]++; } if (result.Item4 == Result.One) { initedQubitsValues[3]++; } if (result.Item5 == Result.One) { initedQubitsValues[4]++; } } Console.WriteLine($"Qubit-0 initiations: {initedQubitsValues[0]}"); Console.WriteLine($"Qubit-1 initiations: {initedQubitsValues[1]}"); Console.WriteLine($"Qubit-2 initiations: {initedQubitsValues[2]}"); Console.WriteLine($"Qubit-3 initiations: {initedQubitsValues[3]}"); Console.WriteLine($"Qubit-4 initiations: {initedQubitsValues[4]}"); } }

Etwas ist schief gelaufen. Eine nahezu gleichmäßige Verteilung wurde erwartet. Der Grund ist einfach: In Schritt 3 habe ich das dritte Qubit anstelle des ersten invertiert: (Controlled (X)) ([Register [0], Register [2]], Register [3]); ~~nicht~~ gute alte Copy-Paste.

Wir korrigieren den Code und führen den Test durch:

Initiierung korrigiert

  // Inits fox holes, with almost equal probabilities operation InitFoxHoles(register: Qubit[]) : Unit { body { ResetAll(register); // Step 1 H(register[0]); H(register[2]); // Step 2 (Controlled (X))([register[0],register[2]], register[3]); // Step 3 X(register[0]); X(register[2]); (Controlled (X))([register[0],register[2]], register[1]); X(register[0]); X(register[2]); // Step 4 CNOT(register[3], register[0]); CNOT(register[3], register[2]); // Step 5 (Controlled (H))([register[3]], register[4]); // Step 6 CNOT(register[4], register[3]); } } }

Schon besser. Der Code ist in der Rübe, Version Commit 1, zu sehen .

Wo soll der Fuchs laufen?

Wählen Sie das fünfte Qubit (die Nummerierung beginnt von oben) unter der aktuellen Richtung des Fuchses. Wir sind uns einig, dass Null eine Abwärtsbewegung bedeutet, eine Einheit eine Aufwärtsbewegung. Wenn sich der Fuchs bereits im Nullloch befindet, sollte er sich natürlich nach unten bewegen. Befindet sich der Fuchs im vierten Loch, bewegt er sich nach oben. In anderen Fällen kann sich der Fuchs auf und ab bewegen. Nach diesen einfachen Regeln können wir das „Qubit der aktuellen Richtung“ auf 0, 1 oder eine Überlagerung von Null und Eins setzen. Wir sehen uns den Code im Repository Commit 2 an .

Schema im Editor.

Code und Test

 // Select next Fox movement direction, updating qubit 5 // 1 means go up (4 -> 3, 3 -> 2, ... 1 -> 0) // 0 means go down (0 -> 1, 1 -> 2, ... 3 -> 4) operation SetupMovementDirection(qubits: Qubit[]) : Unit { body { // Step 1 CNOT(qubits[4], qubits[5]); // Step 2 (Controlled (H))([qubits[3]], qubits[5]); // Step 3 (Controlled (H))([qubits[2]], qubits[5]); // Step 4 (Controlled (H))([qubits[1]], qubits[5]); } } operation TestMovementDirectionSetup(): (Result, Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; mutable res5 = Zero; using(qubits=Qubit[16]) { InitFoxHoles(qubits); SetupMovementDirection(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); set res5 = M(qubits[5]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4, res5); } }

  static void TestMovementDirectionSetup() { using (var sim = new QuantumSimulator()) { List<string> results = new List<string>(); string initedCubit = null; string moveDirection = null; for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result, Result) result = Quantum.FoxHunter.TestMovementDirectionSetup.Run(sim).Result; if (result.Item1 == Result.One) { initedCubit = "0"; } if (result.Item2 == Result.One) { initedCubit = "1"; } if (result.Item3 == Result.One) { initedCubit = "2"; } if (result.Item4 == Result.One) { initedCubit = "3"; } if (result.Item5 == Result.One) { initedCubit = "4"; } if (result.Item6 == Result.One) { moveDirection = "1"; } else { moveDirection = "0"; } results.Add($"{initedCubit}{moveDirection}"); } foreach(var group in results .GroupBy(result => result) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} was measured {group.Count()} times"); } Console.WriteLine($"\r\nTotal measures: {results.Count()}"); } }

Bewegung

Implementiert von kontrolliertem SWAP. Wenn das steuernde Qubit einfach ist, tauschen Sie es aus. Wenn das steuernde Qubit Null ist, tauschen wir auf.

Schema im Editor .

Q # Operator

  // Makes a movement based on the 5'th qubit value // 1 means go up (4 -> 3, 3 -> 2, ... 1 -> 0) // 0 means go down (0 -> 1, 1 -> 2, ... 3 -> 4) operation MakeMovement(qubits: Qubit[]) : Unit { body { // Code movement Up // Step 1 mutable qubitsToSwap = [qubits[0], qubits[1]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 2 set qubitsToSwap = [qubits[1], qubits[2]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 3 set qubitsToSwap = [qubits[2], qubits[3]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 4 set qubitsToSwap = [qubits[3], qubits[4]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // COde movement down X(qubits[5]); // Invert direction qubit for the ZeroControlled operations // Step 5 set qubitsToSwap = [qubits[3], qubits[4]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 6 set qubitsToSwap = [qubits[2], qubits[3]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 7 set qubitsToSwap = [qubits[1], qubits[2]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); // Step 8 set qubitsToSwap = [qubits[0], qubits[1]]; (Controlled(SwapReverseRegister))([qubits[5]],qubitsToSwap); X(qubits[5]); // Back-invert for the direction qubit } }

Q #: Anweisung für Tests

  operation TestFirstMovement(): (Result, Result, Result, Result, Result, Result) { body { mutable res0 = Zero; mutable res1 = Zero; mutable res2 = Zero; mutable res3 = Zero; mutable res4 = Zero; mutable res5 = Zero; using(qubits=Qubit[16]) { InitFoxHoles(qubits); SetupMovementDirection(qubits); MakeMovement(qubits); set res0 = M(qubits[0]); set res1 = M(qubits[1]); set res2 = M(qubits[2]); set res3 = M(qubits[3]); set res4 = M(qubits[4]); set res5 = M(qubits[5]); ResetAll(qubits); // ALWAYS clean after yourself } return (res0, res1, res2, res3, res4, res5); } }

C # -Code

  static void TestFirstMove() { using (var sim = new QuantumSimulator()) { List<string> results = new List<string>(); string initedCubit = null; string moveDirection = null; for (int i = 0; i < 1000; i++) { (Result, Result, Result, Result, Result, Result) result = Quantum.FoxHunter.TestFirstMovement.Run(sim).Result; if (result.Item1 == Result.One) { initedCubit = "0"; } if (result.Item2 == Result.One) { initedCubit = "1"; } if (result.Item3 == Result.One) { initedCubit = "2"; } if (result.Item4 == Result.One) { initedCubit = "3"; } if (result.Item5 == Result.One) { initedCubit = "4"; } if (result.Item6 == Result.One) { moveDirection = "1"; } else { moveDirection = "0"; } results.Add($"{initedCubit}{moveDirection}"); } // Holes measurements foreach (var group in results .GroupBy(result => result[0]) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} hole was measured {group.Count()} times"); } // Directions measuremetns foreach (var group in results .GroupBy(result => result[1]) .OrderBy(group => group.Key)) { Console.WriteLine($"{group.Key} direction was measured {group.Count()} times"); } Console.WriteLine($"\r\nTotal measures: {results.Count()}"); } }

Der Code kann in Commit 3 angezeigt werden.

Wir machen 6 Züge

Schließlich wählen wir das sechste Qubit für den Status des Spiels (der Fuchs ist frei / der Fuchs ist nicht frei). Die Einheit entspricht einem freien Fuchs. Wir werden weitere Schritte nur mit einem einzigen Status-Qubit machen.

Die Qubits 7,8,9,10,11 werden eine Bewegungsgeschichte führen. Nach jedem Zug tauschen wir einen von ihnen gegen ein Qubit der aktuellen Richtung aus (dies ermöglicht es uns, den Verlauf der Züge zu speichern und das Qubit der aktuellen Richtung vor jedem Zug zurückzusetzen).

Schema beigefügt .

Q # Operator

  /// Make 6 movements. Every movement is controlled by the 6'th qubit. /// After the every qubit we check if the fox has been captured and invert the 6'th qubit /// Reminder: 6'th qubit equal to One means "Fox is free, go further" operation MakeSixMovements(qubits: Qubit[]) : Unit { body { // Move 1 (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Reverse Fox State if it's shot // Move 2 SwapReverseRegister([qubits[5], qubits[7]]); // Move the first move direction to the qubit 7, qubit 5 is Zero again (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 3 SwapReverseRegister([qubits[5], qubits[8]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); // Move 4 SwapReverseRegister([qubits[5], qubits[9]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Move 5 SwapReverseRegister([qubits[5], qubits[10]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 6 SwapReverseRegister([qubits[5], qubits[11]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); } }

Q #: Anweisung für Tests

  operation TestSixMovements(): (Result) { body { mutable res = Zero; using(qubits=Qubit[16]) { ResetAll(qubits); InitFoxHoles(qubits); X(qubits[6]); // At the beginning of the game our fox is alive MakeSixMovements(qubits); set res = M(qubits[6]); ResetAll(qubits); // ALWAYS clean after yourself } return (res); } }

C #: Testen

  static void TestMovements() { using (var sim = new QuantumSimulator()) { int zerosCount = 0; for (int i = 0; i < 1000; i++) { Result result = Quantum.FoxHunter.TestSixMovements.Run(sim).Result; if(result == Result.Zero) { zerosCount++; } } Console.WriteLine($"\r\nTotal zeroes: {zerosCount}"); } }

Wir sehen Commit 4 .

Feinschliff

Wir haben einen Fehler in der Schaltung. Da wir die Strategie 1-2-3-1-2-3 testen, überprüfen wir jedes Loch zweimal. Nachdem wir den Fuchs im ersten Zug gefangen haben, werden wir das Status-Qubit zweimal durchlaufen (im ersten und vierten Zug).

Um diese Situation zu vermeiden, verwenden wir 12 Qubits, um den Status nach den Zügen 4-5-6 zu korrigieren. Zusätzlich fügen wir die Definition des Sieges hinzu: Wenn mindestens eines der Status-Qubits auf Null geht, haben wir gewonnen.

Das endgültige Schema .

Q #: Korrigieren Sie den 6-Zug-Operator

  operation MakeSixMovements(qubits: Qubit[]) : Unit { body { // Move 1 (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[1], qubits[6]); // Reverse Fox State if it's shot // Move 2 SwapReverseRegister([qubits[5], qubits[7]]); // Move the first move direction to the qubit 7, qubit 5 is Zero again (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[2], qubits[6]); // Move 3 SwapReverseRegister([qubits[5], qubits[8]]); (Controlled(SetupMovementDirection))([qubits[6]],(qubits)); (Controlled(MakeMovement))([qubits[6]],(qubits)); CNOT(qubits[3], qubits[6]); // Move 4 SwapReverseRegister([qubits[5], qubits[9]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[1], qubits[12]); // Move 5 SwapReverseRegister([qubits[5], qubits[10]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[2], qubits[12]); // Move 6 SwapReverseRegister([qubits[5], qubits[11]]); (Controlled(SetupMovementDirection))([qubits[6], qubits[12]],(qubits)); (Controlled(MakeMovement))([qubits[6], qubits[12]],(qubits)); CNOT(qubits[3], qubits[12]); } }

F #: Festlegen der Operator-Teststrategie 1-2-3-1-2-3

  operation TestStrategy () : (Result) { // 0..4 - holes // 5 - current movement direction. Zero means "go down", One means "go up" // 6 - Game status. 1 means "fox is free, go further" // 7,8,9,10, 11 - movements history // 12 - another qubit of the fox live. 1 means "fox is still free, go further" // 13 Result qubit. If it's zero, the fox is alive body { mutable res = Zero; using(qubits=Qubit[14]) { ResetAll(qubits); // Init fox positions and the fox' live InitFoxHoles(qubits); X(qubits[6]); // At the beginning of the game our fox is alive X(qubits[12]); // The second qubit of the fox live. If it's one - the fox is alive. // Make moves MakeSixMovements(qubits); // Measure results. If the 13'th qubit is zero the fox is alive X(qubits[6]); X(qubits[12]); CNOT(qubits[6], qubits[13]); CNOT(qubits[12], qubits[13]); CCNOT(qubits[6], qubits[12], qubits[13]); set res = M(qubits[13]); ResetAll(qubits); // ALWAYS clean after yourself } return (res); } }

C #: Endprüfung durchführen

  static void RunFoxHunt() { Stopwatch sw = new Stopwatch(); sw.Start(); using (var sim = new QuantumSimulator()) { var foxSurvives = 0; var hunterWins = 0; for (int i = 0; i < 1000; i++) { var result = (Result)(TestStrategy.Run(sim).Result); if (result == Result.Zero) { foxSurvives++; } else { hunterWins++; } } Console.WriteLine($"Fox survives: \t{foxSurvives}"); Console.WriteLine($"Hunter wins: \t{hunterWins}"); } sw.Stop(); Console.WriteLine($"Experiment finished. " + $"Time spent: {sw.ElapsedMilliseconds / 1000} seconds"); }

Festschreiben 5 .

Was folgt daraus

Grundsätzlich kann das Schema sowohl in der Anzahl der Qubits als auch in der Anzahl der Operationen optimiert werden. Die triviale Optimierung für die Anzahl der Qubits besteht darin, Qubit-13 zu entfernen und nur 6 und 12 zurückzugeben. Optimierung für Operationen - um den ersten Schuss unmittelbar nach der Initiierung zu machen. Überlassen wir diese Arbeit jedoch den Google-Ingenieuren.

Wie Sie sehen, kann jeder, der oberflächlich mit Quantencomputern vertraut ist, sicher den "Fuchsjäger" spielen. Wenn wir etwas mehr Qubits hätten, könnten wir die optimale Lösung finden und nicht die vorhandene überprüfen. Es ist durchaus möglich, dass Tic-Tac-Toe (und ihre Quantenversion), Dame, Schach, Go als nächstes fallen.

Gleichzeitig bleibt das Thema "Lösbarkeit" von Spielen wie DotA, Starcraft und Doom offen. Für das Quantencomputing ist die Speicherung der gesamten Klickhistorie charakteristisch. Wir nehmen einen APM (Actions Per Minute) von 500, multiplizieren mit der Anzahl der Spieler, multiplizieren mit der Anzahl der Minuten, addieren die Zufälligkeit des Spiels selbst - die Anzahl der Qubits, die zum Speichern aller Informationen erforderlich sind, wächst zu schnell.

Die Auswahl eines Spiels in einem kleinen Wettbewerb zwischen Brin und Page kann also eine entscheidende Rolle spielen. Die Entwicklung eines „ebenso schwierigen“ Spiels für klassische Computer und Quantencomputer verdient jedoch eine eigene Theorie.

Quantencomputer in Spielen oder ernsthaft verrückt werden