Dass wir eine Straße bauen sollen. Teil 1

Die tägliche Reiseroute der meisten von uns beschränkt sich auf Reisen von zu Hause zur Arbeit und zurück. Und das schwierigste Hindernis, das unsere Bewegung verlangsamen kann, sind Staus. Aber in unserem Land gibt es eine Vielzahl von Orten, an denen Sie nur mit Spezialfahrzeugen aussteigen können.

Ein solcher Transport ist gut, wenn Sie keine großen Mengen an Fracht befördern oder regelmäßig in solche unzugänglichen Gebiete reisen müssen. Dann sollten wir schon über den Aufbau einer Infrastruktur nachdenken, deren Bewegung mit dem üblichen zivilen Verkehr möglich ist.

Und es ist gut, wenn die gesamte Komplexität beim Entwerfen einer zukünftigen Route darin besteht, ein Lineal und einen Bleistift zu finden, um eine gerade Linie auf der Karte zu zeichnen, die einige Objekte verbindet. Aber leider sieht unsere Realität ganz anders aus. Was ist, wenn das darüber fliegende Gelände einem guten Stück Schweizer Käse ähnelt?

Seit mehr als einem Jahr arbeiten wir mit Kollegen des Forschungslabors Digital Design zusammen, um ein Tool zu entwickeln, mit dem verschiedene Kommunikationsnetzwerke im automatischen Modus aufgebaut werden können. Für Details willkommen bei Katze.

Wie alles begann

Reisen zu solchen abgelegenen Orten sind in der Regel auf bestimmte finanzielle Vorteile zurückzuführen. Und obwohl oft im Voraus bekannt ist, dass die Entwicklung dieser Gebiete gute Gewinne bringen wird, warum nicht Geld für Dinge sparen, die ohne besondere Schwierigkeiten erledigt werden können? Was ist, wenn eine besser gestaltete Route es uns ermöglicht, nicht mehrere zusätzliche Kilometer der Autobahn zu bauen?

Aber nur die Verfügbarkeit von Straßen, um einen signifikanten Gewinn zu erzielen, reicht eindeutig nicht aus. Und im Grunde wird es nur durch Mineralvorkommen gebracht. Daher ist es neben Straßen erforderlich, ein Netz verschiedener Rohrleitungen, ein Netz von Wasserleitungen und ein Netz von Stromleitungen mit korrekt platzierten Umspannwerken zu entwerfen. All diese Infrastrukturen können als lineare Objekte bezeichnet werden.

Und wenn ein Ingenieur vor der Aufgabe steht, ein Kommunikationsnetz vor Ort mit komplexen technischen und geologischen Bedingungen zu entwerfen, fällt ihm eine unglaublich komplexe analytische Aufgabe zu.

Wie komme ich nicht in die Flussflutzone? Wie kann der Pfad auf Permafrostböden minimiert werden? Wie kann man beim Verlegen einer Straße durch einen Sumpf viel Sandkissen sparen? Woher bekommt man Sand für dieses Kissen?

Dies ist nur ein kleiner Teil der Fragen, die sich ein Ingenieur während der Arbeit stellt, und dennoch müssen Sie verschiedene GOSTs und SNiPs berücksichtigen. Und wenn Sie nur zwei Objekte verbinden möchten und wenn es ein paar Dutzend Objekte gibt?

Daher benötigt die Konstruktionsbranche dringend ein Werkzeug, mit dem sowohl die Kosten für von einem Ingenieur entworfene lineare Objekte als auch die Fähigkeit, sie im automatischen Modus zu erstellen, berechnet werden können.

Daten

Das erste, was wir zu Beginn der Aufgabe erledigen mussten, war die Datensuche. Welche Daten werden benötigt? Wo bekommt man sie? Und wenn die zweite Frage mit Hilfe des Benutzers gelöst werden kann, brauchten wir ernsthafte Analysen, um die erste Frage zu verstehen.

Und die Daten für die korrekte Berechnung brauchen wirklich viel - angefangen von der banalsten Markierung des Gebiets, auf dem Seen und Flüsse markiert sind, verschiedenen Sümpfen sowie Karstgebieten, auf denen aufgrund der drohenden Kollapsbildung dringend empfohlen wird, nicht zu bauen. Daher werden hier neben den vom Satelliten aus sichtbaren Gebieten auch Daten aus geologischen Untersuchungen des Gebiets benötigt.

Aber nicht alle Daten sind auf natürliche Objekte in unserem Land beschränkt. Es gibt auch eine Reihe von Dingen, die vom Menschen geschaffen wurden. Zum Beispiel können wir beim Straßenbau die früher gebauten Straßen verwenden. Beim Bau von Pipelines ist die Nutzung der vorhandenen Infrastruktur jedoch bei weitem nicht immer möglich. Da der Anschluss einer neuen Pipeline an ein bestehendes Netzwerk möglicherweise die hydraulische Berechnung nicht besteht.

Neben der Wiederverwendung dessen, was zuvor vom Menschen geschaffen wurde, müssen auch verschiedene Einschränkungen beim Bau in der Nähe von Objekten berücksichtigt werden. Beispielsweise müssen beim Bau von Stromleitungen Einkerbungen von menschlichen Wohnorten in Abhängigkeit von der Spannung an der Stromleitung selbst berücksichtigt werden.

Es ist jedoch nicht ganz richtig, die Berechnung des Problems nur in einer Ebene zu betrachten, da es neben flachem Gelände auch Gebiete mit großen Höhenunterschieden gibt, auf denen auch keine Bauarbeiten durchgeführt werden können.

Das Abrufen von Daten auf dem Gelände ist viel einfacher als das Abrufen von Daten auf Gebieten und der vorhandenen Infrastruktur. Um die Entwicklung zu vereinfachen, verwenden wir offene SRTM-Höhendaten (Shuttle Radar Topography Mission), die jeder erhalten kann.

Wir haben also die Daten, wir wissen, wo wir bauen können, wo wir nicht bauen können, es gibt Baukosten für verschiedene Bereiche des Geländes. Wir haben eine Region, es gibt eine Reihe von Objekten, die wir zu einem einzigen Kommunikationsnetzwerk verbinden möchten. In mathematischen Begriffen klingt dies wie eine Suche nach einer Lösung für das Steiner-Problem.

Ein bisschen Mathe

Es ist bekannt, dass jede Formel die Anzahl der Leser halbiert, daher haben wir diesen Abschnitt drastisch reduziert ...

Um die Route der geplanten linearen Anlage zu optimieren, müssen die Baukosten berechnet werden können. Jedes lineare Objekt kann als Polylinie dargestellt werden $$$L = \ {A_i, B_i \} _ {i = 0} ^ n$ bestehend aus Segmenten $$$AB_ {i}$.
Die Baukosten jedes geraden Abschnitts können als Funktionswert dargestellt werden $$$C_ {AB_ {i}}$, wobei jedes Segment parametrisch angegeben wird:

$$$$ display $$ {\ displaystyle AB_i \ Doppelpunkt \ links \ {{\ begin {ausgerichtet} & s = s \ links (t \ rechts) - \ mbox {parametrisierte Kurve}, \\ & h = h \ links (s (t) ) \ rechts) - \ mbox {Funktion der Höhenhöhe}, \\ & c = c \ links (s (t) \ rechts) - \ mbox {Funktion der Baustückkosten an einem Punkt}, \\ \ Ende {ausgerichtet}} \ rechts .} $$ display $$

wo $$$t \ in \ left [0, 1 \ right]$- Segmentparametrierung.

$$$C_ {AB_i} = \ int \ Grenzen_ {AB_i} c \ links (s (t) \ rechts) \ sqrt {\ links [g_ {xy} (s (t)) + \ frac {\ partielle h} {\ partiell s_x} \ cdot \ frac {\ partiell h} {\ partiell s_y} \ rechts] \ dot {s} _ {x} \ dot {s} _ {y}} dt$wo $$$g$- der metrische Tensor der Erdoberfläche ohne Berücksichtigung des Reliefs, dh in einfachen Worten, der Funktion der Messung der Entfernung auf der Erdoberfläche.

Aufgrund der Tatsache, dass unser Planet die Form eines Geoids hat, ist es notwendig, spezielle Formeln zu verwenden, um Entfernungen zu messen. Dafür verwenden wir die Haversinus-Formel. Darin sieht die Form des Planeten wie eine Kugel aus, aber dies reicht für unsere Zwecke aus, da der Messfehler etwa 0,3% beträgt und die Geschwindigkeit der Berechnung von Entfernungen mit dieser Methode hoch bleibt.

Ansätze, um den besten Weg zu finden

Bevor Sie sich jedoch einer Gruppe von Objekten anschließen, müssen Sie lernen, wie Sie den optimalen Pfad zwischen beiden finden. Zwei Möglichkeiten, dies zu tun, kommen sofort in den Sinn:

1. Erstellen Sie ein Diagramm und wenden Sie dann die Suchmethoden für kürzeste Pfade an.
2. Verwenden Sie eine Lösung, die auf Optimierungsmethoden basiert.

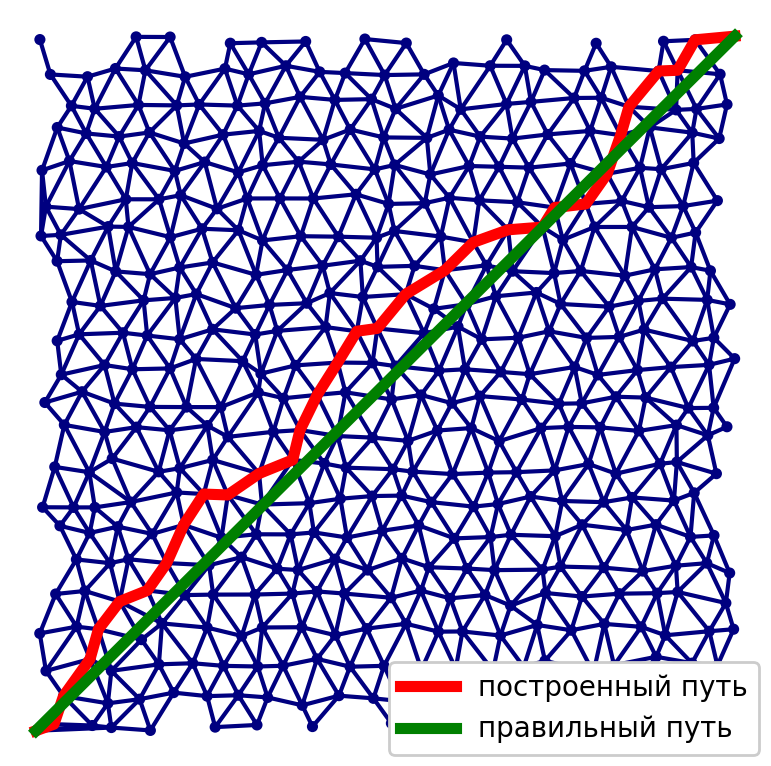
Bei der Implementierung der ersten Methode tritt ein Problem mit der Methode zur Erstellung eines Diagramms auf, um die höchstmögliche Genauigkeit der Lösung zu erzielen. Es ist notwendig, ein Gleichgewicht zwischen der Anzahl der Eckpunkte und Kanten im Diagramm, der Qualität der Lösung und der Zeit zu finden, die für die Berechnung benötigt wird.

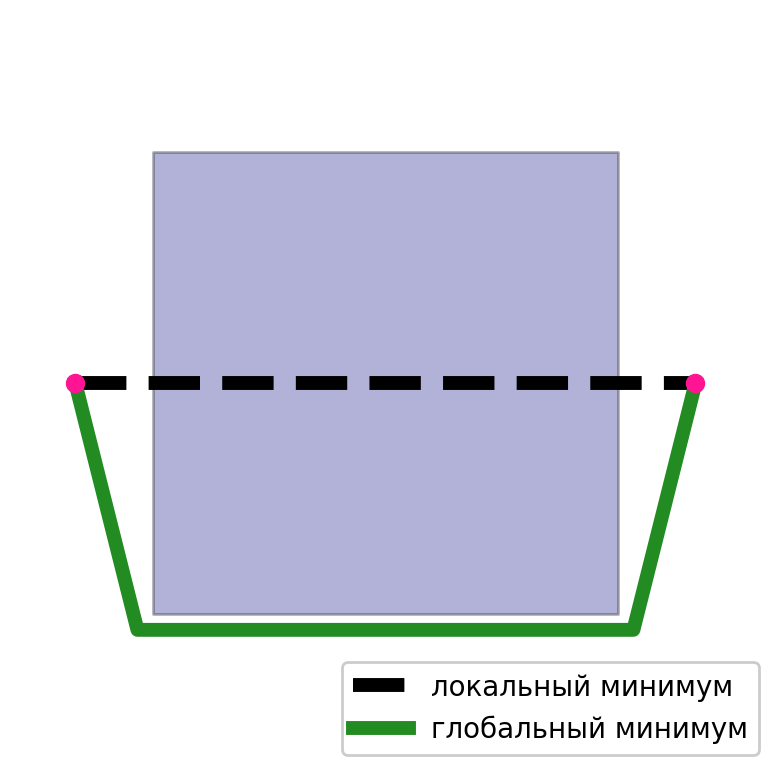
Im zweiten Fall sind die lokalen Minima das Hauptproblem. Es ist einfach, einen Fall auszuwählen, in dem die Lösung möglicherweise nicht konvergiert oder nicht optimal ist. Da die durch dieses Verfahren erhaltene Lösung unglaublich von der anfänglichen Näherung abhängt. Wenn wir eine gute anfängliche Annäherung haben, wird das Ergebnis von hoher Qualität sein.

Wir haben also zwei Ansätze, um dieses Problem zu lösen. Der erste hat eine eher geringe Qualität, aber es gibt kein Problem lokaler Minima. Die zweite hat ein Problem mit lokalen Minima, aber eine qualitativ hochwertige Lösung. Und wenn Sie diese beiden Ansätze richtig kombinieren, verschwinden die Mängel jedes einzelnen. Wir nehmen die im Diagramm erhaltene Lösung als erste Annäherung und wenden dann Optimierungsmethoden darauf an.

In diesem Teil des Artikels werden wir die vorgeschlagene Lösung für dieses Problem in der Grafik genau betrachten.

Werkzeugauswahl

Es wurde ein Aktionsplan entworfen, der nur noch "codiert" werden muss. Da wir in der Anfangsphase des Schreibens der Bewerbung wenig Wissen über den Themenbereich hatten, brauchten wir eine flexible Sprache, damit wir im Falle einiger grober architektonischer Fehleinschätzungen den gesamten Code für ein paar Dosen Abendbier umschreiben konnten. Optional wollte ich auch Bibliotheken für alle Gelegenheiten, um nicht auf die Erfindung von Fahrrädern zurückzugreifen. Daher wurde Python als Hauptprogrammiersprache ausgewählt.

In der Anwendung haben wir einen beeindruckenden technologischen Stack verwendet, der nicht auf Folgendes beschränkt ist:

• formschön für die Arbeit mit geometrischen Daten wie Polygonen und Polylinien;
• Geopandas für bequemes Arbeiten mit formschönen ;
• scipy zum Speichern des berechneten Graphen und zum Finden des kürzesten Pfades darauf sowie zum Finden der minimalen Spannbäume;
• PyTorch für die Arbeit mit der Kostenfunktion;
• Kissen zum Arbeiten mit Bildern.

Implementierung

Das Modul kann in mehrere Stufen unterteilt werden:

• Generierung von Kostenfunktionen;
• rechnerische Gittererzeugung;
• Erstellen eines Diagramms basierend auf einem Raster;
• Graphgewichtung;
• Berechnung der kürzesten Wege in einem Diagramm.

Da die Kanten des Diagramms Segmente sind, können wir diese Kanten gewichten, indem wir den Wert eines bestimmten Integrals berechnen, der oben dargestellt ist. Das Diagramm enthält jedoch viele Kanten, und dementsprechend müssen die Kosten- und Höhenwerte für eine sehr große Anzahl von Punkten ermittelt werden, was viel Zeit in Anspruch nehmen kann.

Ursprünglich bestand die Idee darin, die Baustückkosten zu ermitteln, indem ermittelt wurde, ob ein Punkt zu einem Polygon gehört. Diese Idee wurde jedoch aufgrund der hohen algorithmischen Komplexität dieses Ansatzes festgestellt, da es viele Polygone geben kann und jedes von ihnen eine große Anzahl von Eckpunkten aufweist.

Um dieses Problem zu lösen, können wir daher alle vorhandenen Polygone in Form eines Bildes darstellen, das in mathematischer Form eine Matrix ist. Somit können wir die Stückkosten für den Bau an einem Punkt jenseits von O (1) erhalten , und daher können wir die Kosten für den Bau einer bestimmten Rippe mit hoher Genauigkeit erhalten.

Jetzt sind wir bereit, ein Diagramm zu erstellen, aber es gibt keinen eindeutig korrekten Weg, es zu erstellen, um hochpräzise Lösungen zu erhalten. Um einen Graphen zu erstellen, muss ein Berechnungsgitter erzeugt werden, nämlich eine Menge von Punkten in dem betrachteten Bereich, die in der entsprechenden Reihenfolge durch Segmente verbunden sind, die die Flächen der Zellen bilden. Gitter können in zwei Typen unterteilt werden: gleichmäßig und ungleichmäßig.

Das einheitliche Gittermodell beschreibt die Koordinaten einzelner Punkte, so dass der Abstand zwischen den Gitterknoten gleich ist. Ein ungleichmäßiges Gitter wird als zufälliger Satz einzelner Punkte angezeigt.

Die Verwendung eines einheitlichen Gitters liefert nicht immer ein qualitativ hochwertiges Ergebnis, um den kürzesten Weg zu finden. Daher ist es erforderlich, diesen Ansatz an einem unebenen Gitter zu testen. Am vielseitigsten ist das Dreiecksnetz.

Das Gitter wurde erzeugt, indem Rauschen mit einem bestimmten Koeffizienten in ein einheitliches rechteckiges Gitter eingeführt und dann Delaunay-Triangulationspunkte für diesen Satz von Punkten angewendet wurden.

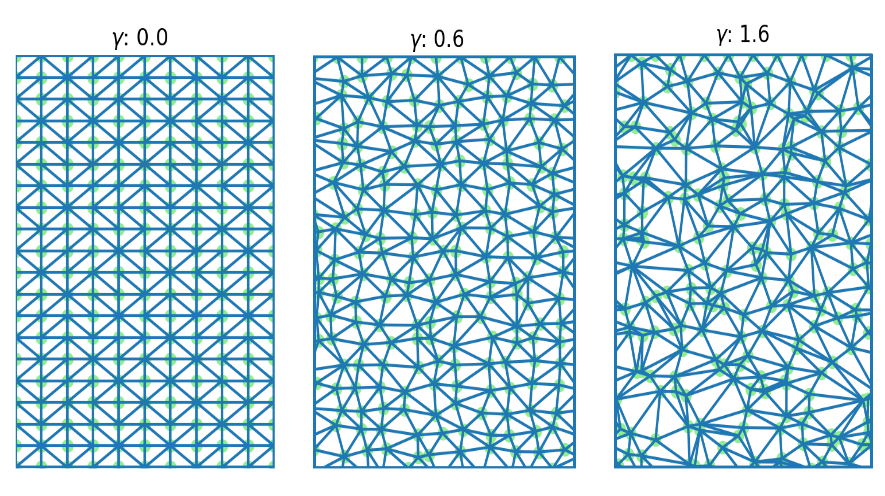
Die Wirksamkeit der konstruierten Gitter wurde auf verschiedenen Modellkarten des Gebiets getestet, wobei die unterschiedlichen Kosten der Regionen und des Reliefs berücksichtigt wurden, und anschließend wurde ein Vergleich mit der analytisch erhaltenen Lösung durchgeführt. Durch Durchsuchen der Länge der Graphkante und des Koeffizienten der Einführung von Rauschen in das gleichmäßige Gitter wurden optimale Parameter gefunden, um den optimalen Pfad zwischen zwei Punkten zu konstruieren.

Hauptprobleme

Zuerst lief alles gut, der Algorithmus berechnete die optimalen Netzwerke, aber sobald es ein Problem mit der Qualität des konstruierten Pfades gab. Der Fall war ganz einfach: Sie mussten zwei Objekte auf einer ziemlich langen Karte verbinden. Der Algorithmus wollte keine Route erstellen, die offensichtlich korrekt war.

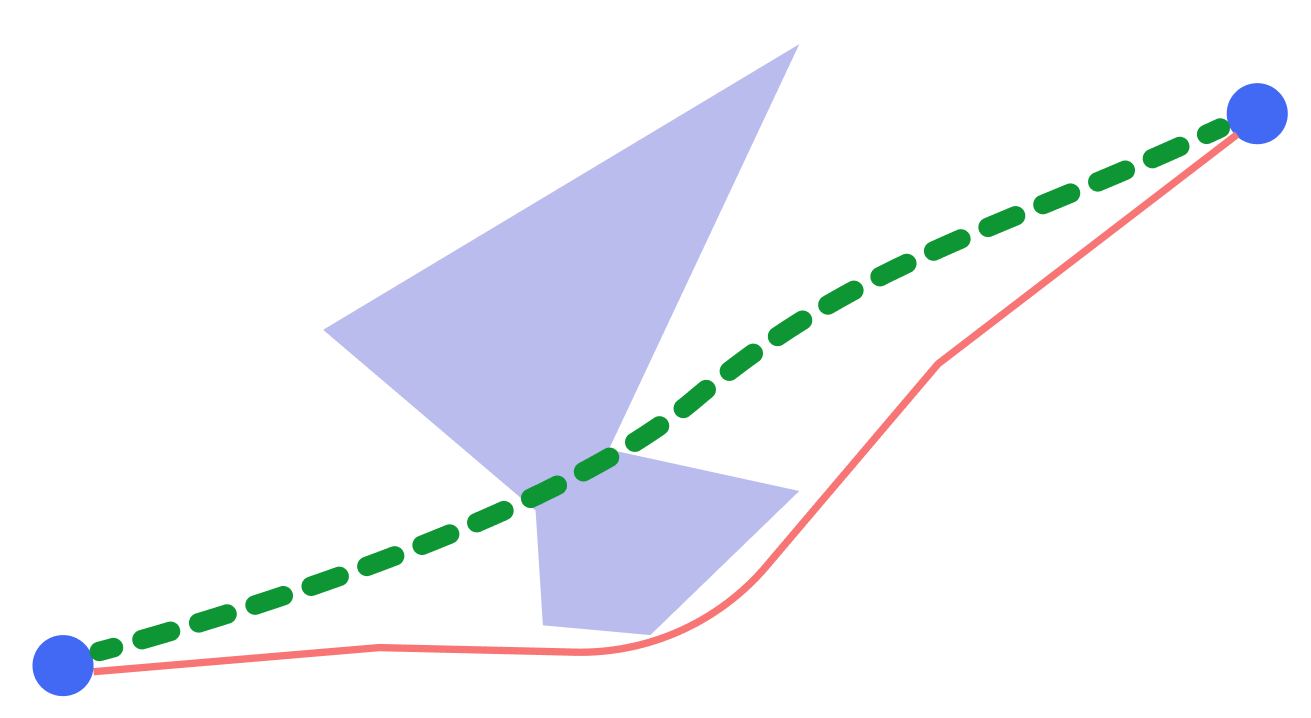
Das Problem war wie immer das Rechenraster. Wir setzten unsere Experimente mit dem Erscheinungsbild der Gitter fort und kamen zu dem Schluss, dass das Verbinden der Scheitelpunkte mit einem Graphen, bei dem jeder Scheitelpunkt mit den n- nächsten Nachbarn verbunden ist, eine Lösung für unsere Probleme darstellt.

Vernetzung

Nachdem wir gelernt hatten, optimale Wege zwischen zwei Punkten zu finden, bestand der nächste Schritt darin, das Problem des Aufbaus eines optimalen Netzwerks linearer Objekte zu lösen. Die in der Literatur vorkommenden Algorithmen zur Konstruktion von Steiner-Bäumen auf Graphen orientieren sich an allgemeineren Problemen und sind daher in unserem Fall unwirksam. Unser Diagramm ist sehr spärlich, mit einer kleinen Anzahl von Endscheitelpunkten im Verhältnis zur Gesamtzahl der Scheitelpunkte im Diagramm, und unsere Aufgabe wird ebenfalls angewendet. Aus einer Reihe anderer Gründe wurde daher beschlossen, einen eigenen Algorithmus zu entwickeln, der eine bestimmte Heuristik verwendet, um effektiv ein optimales Netzwerk aufzubauen.

Die Beschreibung des Algorithmus zum Aufbau des optimalen Netzwerks in der Grafik für unseren Fall ist ein Thema für eine separate Veröffentlichung, wir werden es hier nicht betrachten. Da bei der Berechnung einer realen Aufgabe viele zusätzliche Bedingungen aus der Bauindustrie berücksichtigt werden müssen, die für den Endbenutzer relevant sind und dem verwendeten Algorithmus bestimmte Einschränkungen auferlegen.

Echter Fall

Nun wenden wir uns den Ergebnissen des Algorithmus zu. Unsere Aufgabe ist es, einen bestimmten Satz von Objekten mit einem Kommunikationsnetzwerk zu verbinden. Der Vergleich der Ergebnisse des Algorithmus erfolgte mit einem zuvor gebauten Straßennetz. Die Gesamtlänge des bestehenden Netzes beträgt 153,5 km gegenüber 122,6 km für das berechnete Netz. Dies führt zu einer Reduzierung der Länge des Straßennetzes um etwa 25%, wodurch letztendlich etwa 5 bis 15% der Kapitalkosten für den Bau eingespart werden.

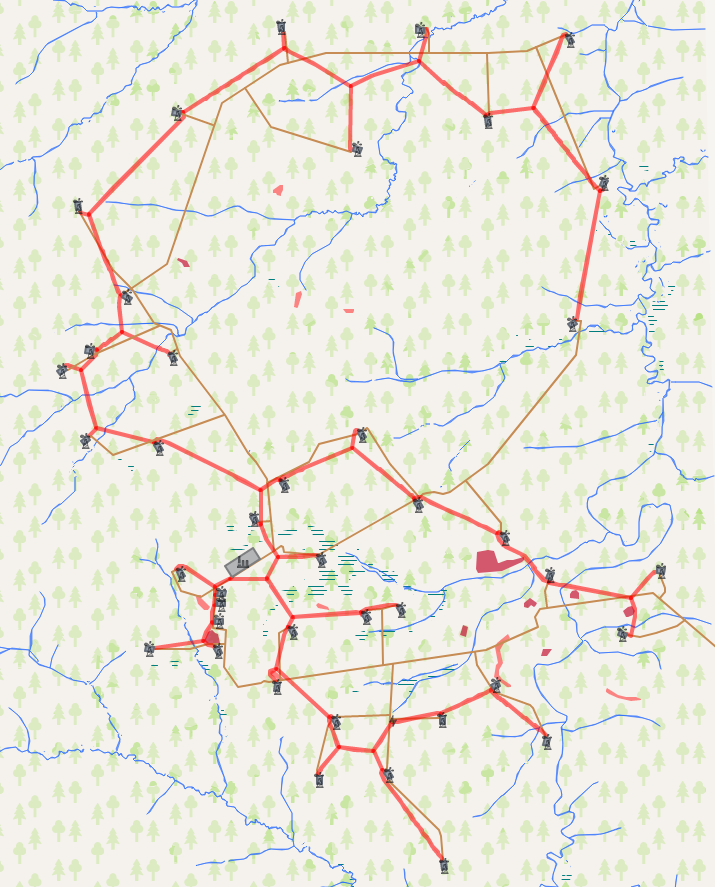
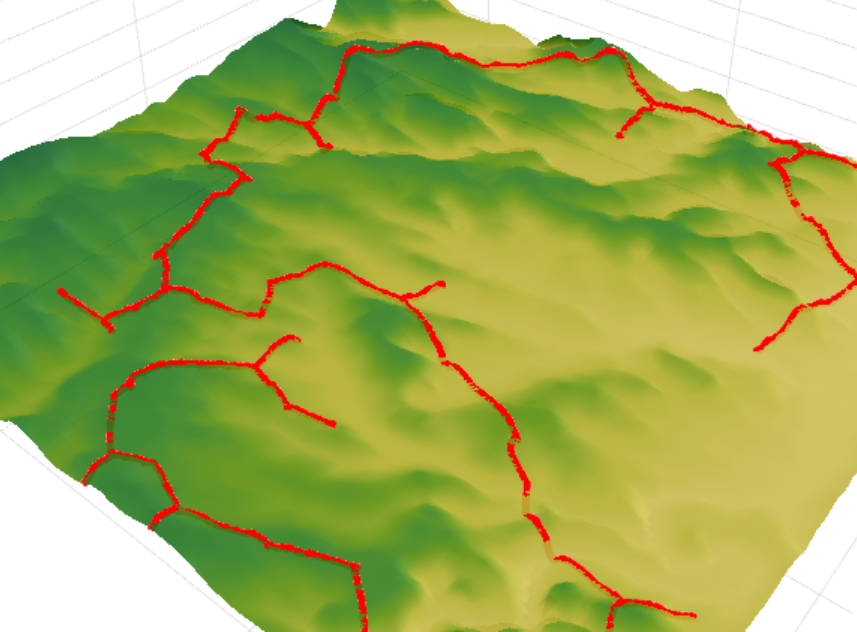
Hier können Sie sich die Berechnungsergebnisse genauer ansehen.

Eine Beschreibung der verwendeten Optimierungsmethoden finden Sie im nächsten Teil des Artikels.