Die mathematischen Grundlagen des automatischen Layouts

Viele Entwickler glauben, dass Auto Layout eine Bremse und ein Problem ist, und es ist äußerst schwierig, es zu debuggen. Und es ist gut, wenn diese Schlussfolgerung auf der Grundlage meiner eigenen Erfahrung gezogen wird, ansonsten ist es nur "Ich habe gehört, ich werde nicht einmal versuchen, mich mit ihm anzufreunden".

Aber vielleicht liegt der Grund nicht draußen, sondern drinnen. Zum Beispiel werden die gefährlichsten Vögel in der Welt des Kasuars Menschen nicht ohne Grund angreifen, sondern nur zur Selbstverteidigung. Versuchen Sie daher für eine Sekunde anzunehmen, dass dies kein schlechtes automatisches Layout ist und Sie es nicht gut genug verstehen und nicht wissen, wie man kocht. Dies hat Anton Sergejew getan und sich mit der Theorie befasst, um alles genau zu verstehen. Wir erhalten einen vorgefertigten Überblick über die mathematischen Grundlagen des automatischen Layouts.




Auto Layout ist ein Layoutsystem . Bevor wir uns damit befassen, lassen Sie uns über den modernen Satz im Allgemeinen sprechen. Dann beschäftigen wir uns mit dem automatischen Layout - wir werden herausfinden, welche Aufgabe es löst und wie es es macht. Berücksichtigen Sie die Funktionen bei der Implementierung von Auto Layout in iOS und versuchen Sie, praktische Tipps zu entwickeln, die Ihnen bei der Arbeit helfen können.

Diese Geschichte wird einem mathematischen Artikel sehr nahe kommen, daher einigen wir uns zunächst auf die Notation, um dieselbe Sprache zu sprechen.


Über den Sprecher: Anton Sergeev ( antonsergeev88 ) arbeitet im Yandex.Mart-Team und befasst sich mit dem mobilen Client für Maps unter iOS. Vor der mobilen Entwicklung beschäftigte er sich mit Kraftwerkssteuerungssystemen, bei denen die Kosten für Fehler im Code zu hoch sind, um toleriert zu werden.

Bezeichnungen

Die linearen Gleichungssysteme sind uns seit der Schule bekannt - sie sind durch eine geschweifte Klammer gekennzeichnet und ihre Lösung ist bereits ohne. Außerdem haben lineare Gleichungssysteme Entitäten, die mit Einschränkungen für das automatische Layout arbeiten. Sie sind durch eine gerade Linie gekennzeichnet.



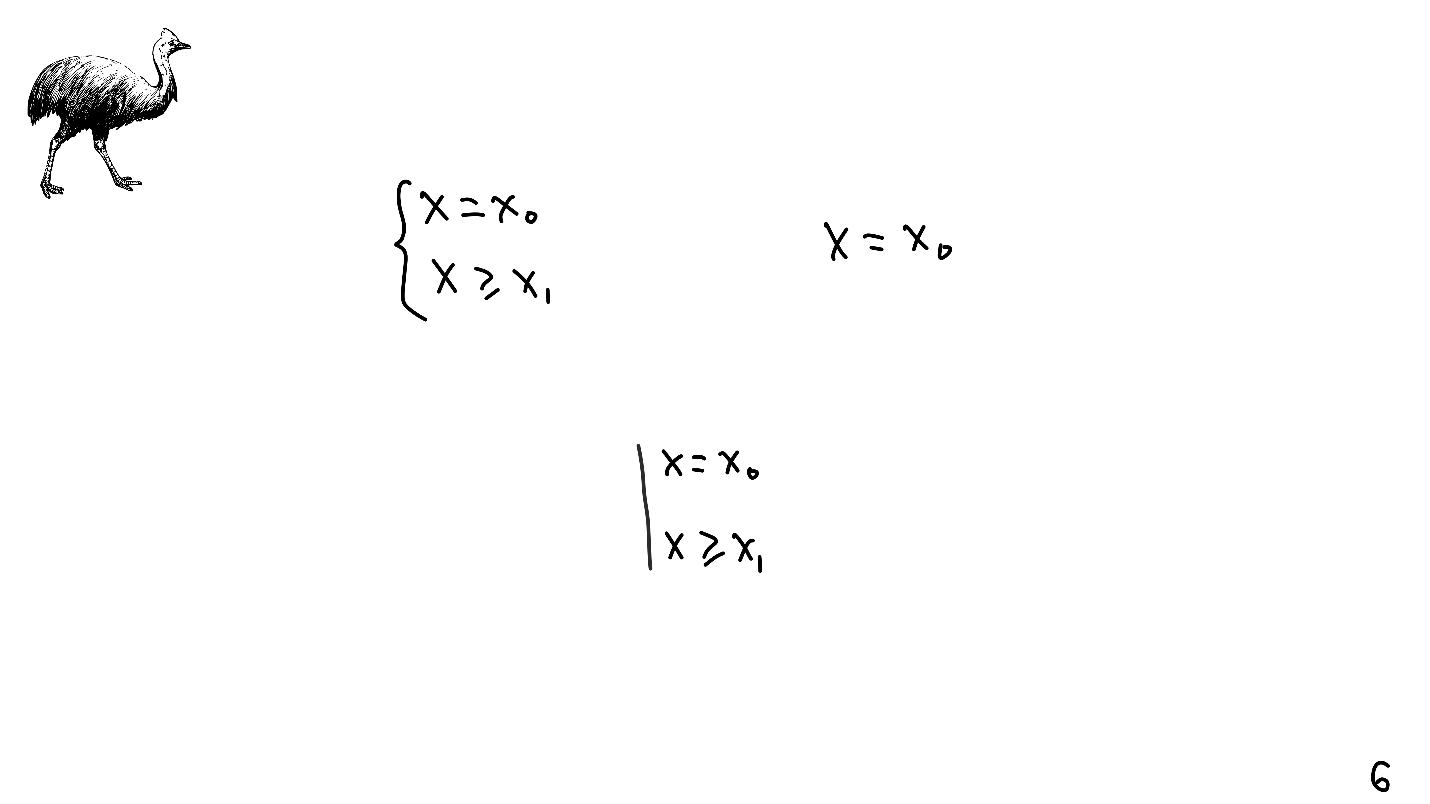
Der seltsame und, wie wir bereits wissen, gefährliche Vogel wird nicht versehentlich in die obere Ecke der Rutsche gemalt. Zu Ehren des Kasuars (lat. Cassowary), der natürlich in Australien lebt, ist in allen unseren iPhones ein Algorithmus benannt.

Das automatische Layout hat seine eigenen Einschränkungen. Wir werden sie mit Farben in der Reihenfolge ihrer Priorität kennzeichnen: Rot - erforderlich; gelb - hoch; blau - niedrig.

Layout

Als ich die Präsentation zusammenstellte, platzierte ich verschiedene Elemente auf dem Bildschirm, zum Beispiel einen Kasuar. Dazu habe ich festgestellt, dass der Kasuar ein rechteckiges Bild ist. Sie müssen es auf einem Blatt anordnen, das Achsen und ein eigenes Koordinatensystem hat, und dafür habe ich die Koordinaten der oberen linken Ecke, Breite und Höhe bestimmt.



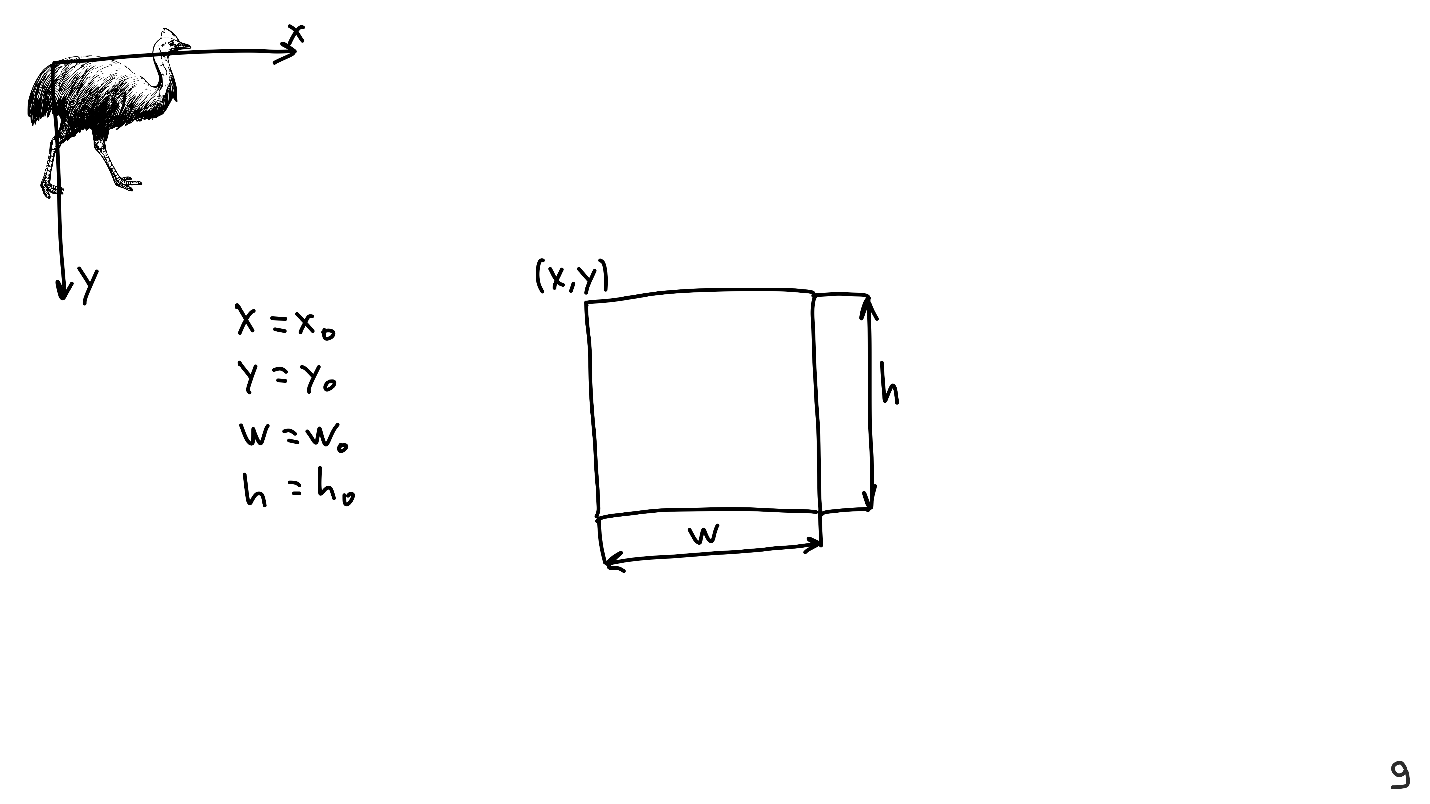
Die Kenntnis dieser vier Werte reicht aus, um jede Ansicht darzustellen.

Algorithmus Nr. 1

Während wir den Kasuar auf das Blatt legten, haben wir den ersten Layout-Algorithmus unauffällig beschrieben:

• Bestimmen Sie die Koordinaten und Größen;
• Wenden Sie sie auf UIView an.

Der Algorithmus funktioniert, ist aber ziemlich schwierig zu verwenden, daher werden wir ihn weiter vereinfachen.

Angenommen, unten ist eine Lösung für ein lineares Gleichungssystem.



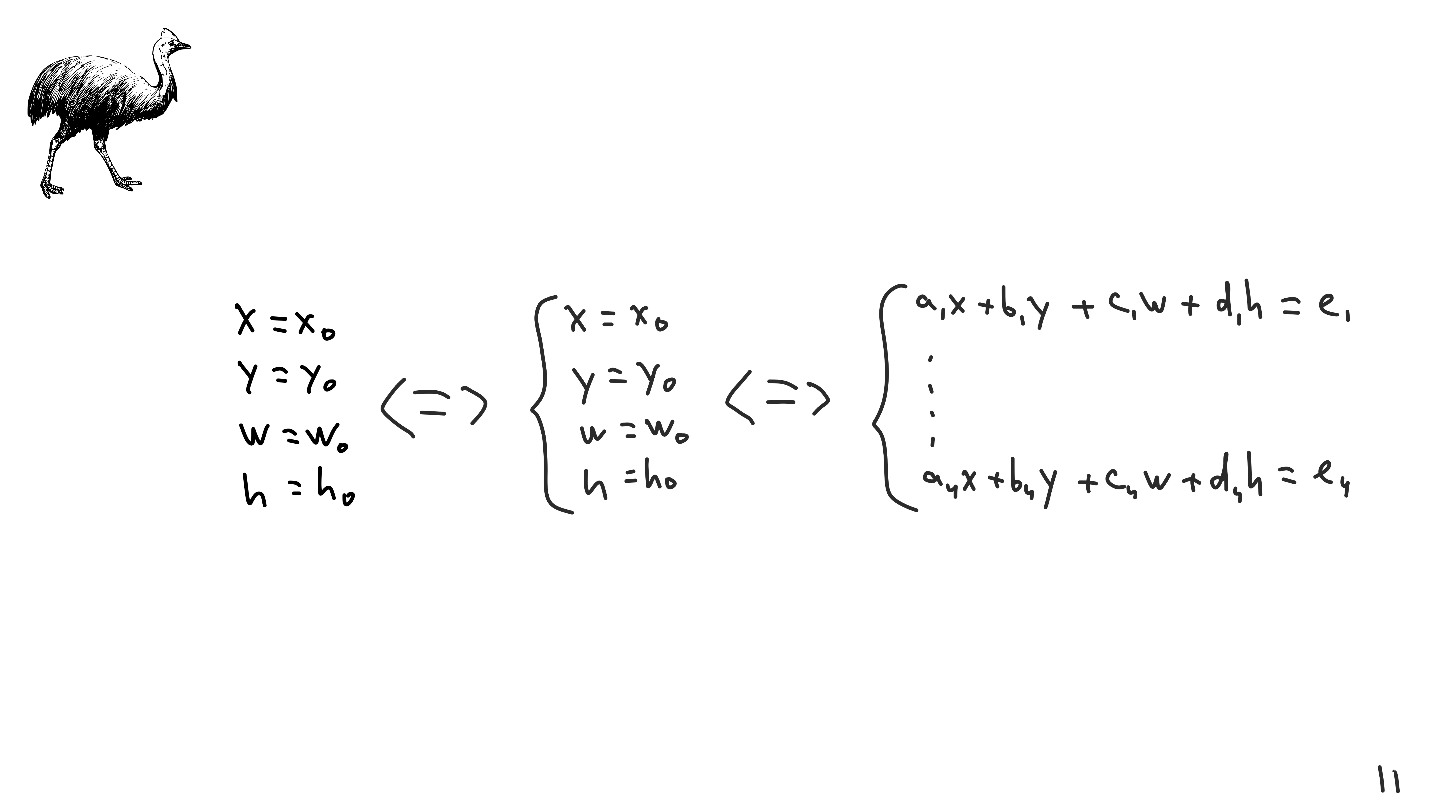
Das System der linearen Gleichungen ist insofern besonders, als viele Operationen darüber definiert sind: Falten von Linien, Multiplizieren mit Konstanten usw. Diese Operationen werden lineare Transformationen genannt, und mit ihrer Hilfe wird das System auf eine beliebige Form reduziert.

Das Schöne an linearen Transformationen ist, dass sie reversibel sind. Dies bringt uns zu einer interessanten und eher subtilen Idee, mit der das gesamte moderne Layout beginnt.

Es soll eine Ansicht geben - ein Rechteck mit seinen Koordinaten und seiner Größe. Wir wollen es so anordnen, dass das Zentrum mit dem gegebenen Punkt übereinstimmt. Wir modellieren das Zentrum mit linearen Transformationen - der Koordinate der oberen linken Ecke + der halben Breite .



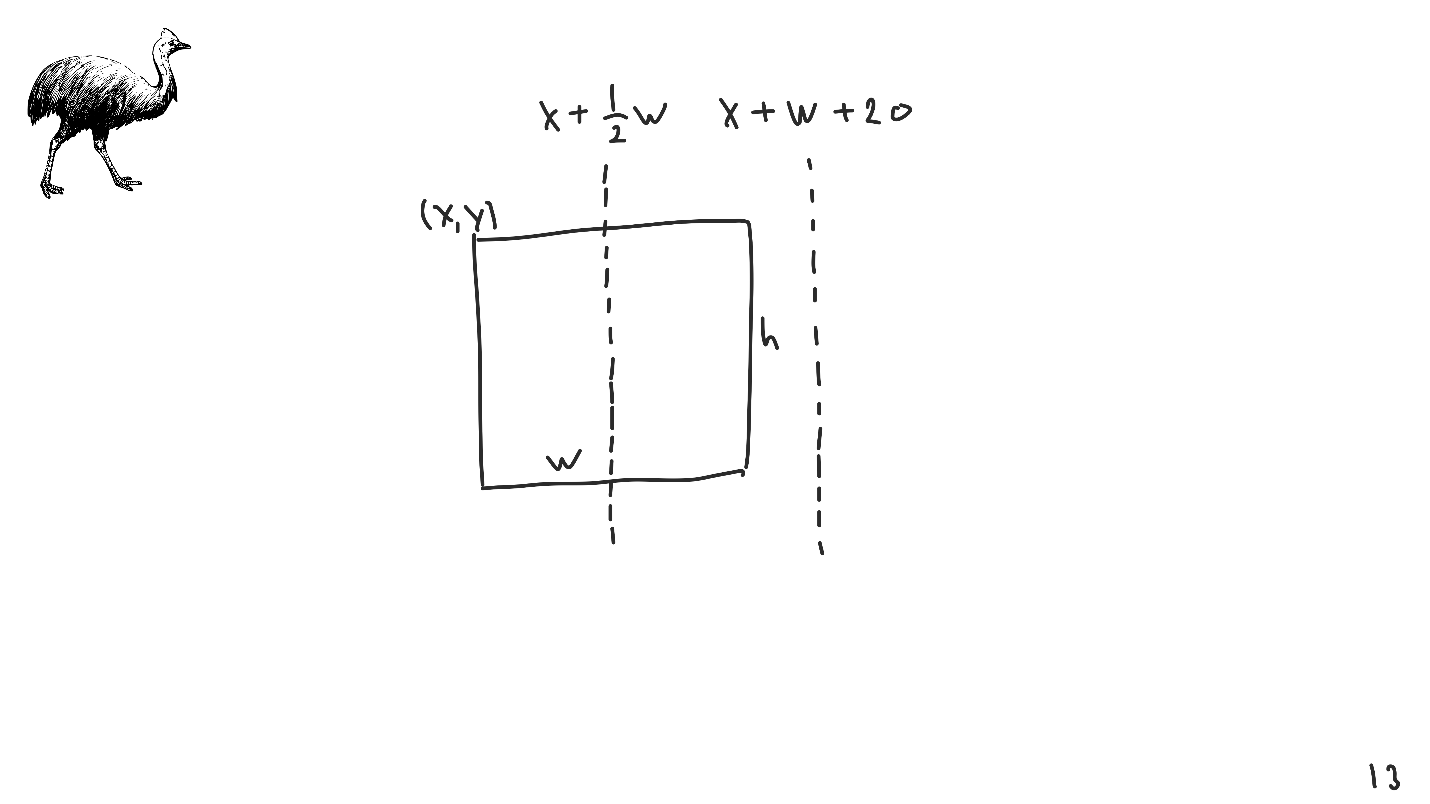
Wir haben das Zentrum durch lineare Transformation modelliert, es war nicht so: Es gab nur die Koordinaten des oberen linken Punktes, der Breite und der Höhe.

Ebenso können Sie jede andere Einrückung simulieren, z. B. 20 Punkte von der rechten Ecke.

Es ist die Idee linearer Transformationen, die es uns ermöglicht, verschiedene Satzsysteme zu erstellen.

Betrachten Sie ein elementares Beispiel. Wir schreiben ein System auf, mit dem wir die Koordinaten der mittleren und rechten Seite, die Breite und das Verhältnis zwischen Breite und Höhe festlegen. Wir lösen das System und bekommen die Antwort.



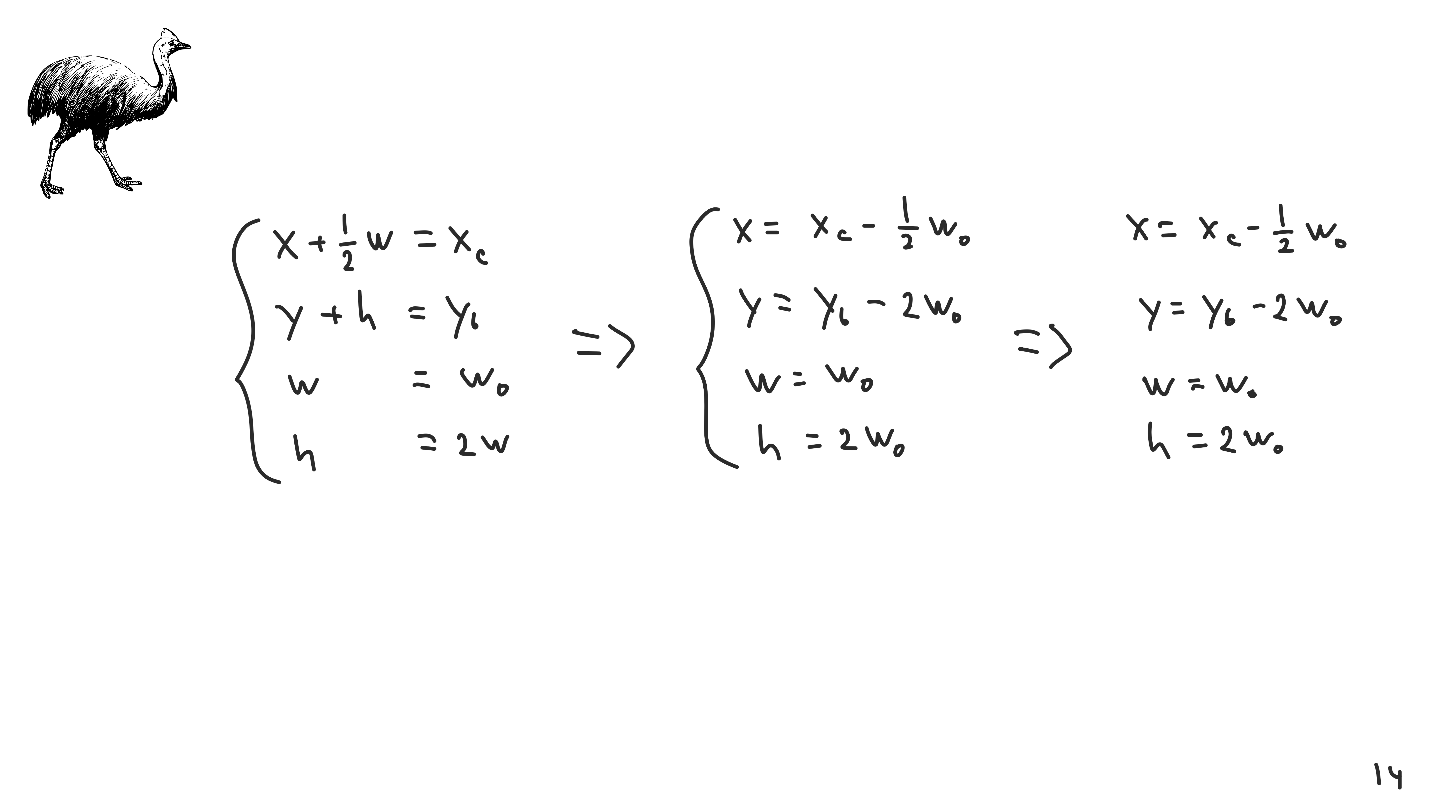
Wir kommen also zum zweiten Algorithmus.

Algorithmus Nr. 2

Die zweite Iteration des Algorithmus besteht aus folgenden Elementen:

• ein lineares Gleichungssystem bilden;
• wir lösen es;
• Wenden Sie die Lösung auf UIView an.

Stellen Sie sich vor, wir befanden uns im 20. Jahrhundert, zu einer Zeit, als die Computerausrüstung noch in den Kinderschuhen steckte, und wir waren die ersten, die unser eigenes Layoutsystem entwickelten. Erfunden, verpackt, dem Benutzer übergeben und er beginnt, es zu verwenden - füllt die Anfangsparameter aus und überträgt es auf unser System.



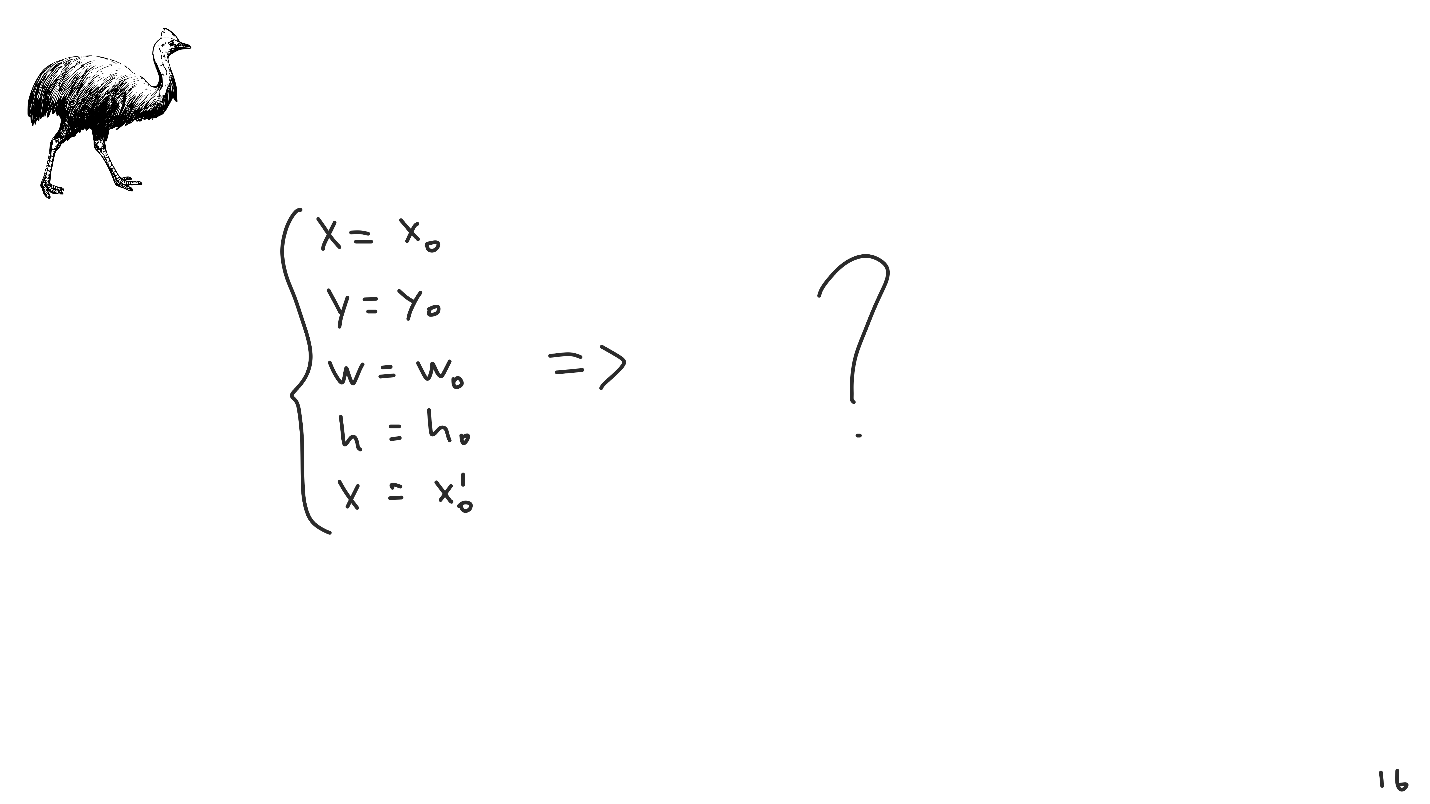
Es gibt ein Problem - dieses System hat keine einzige Lösung. Das Problem ist nicht außergewöhnlich, absolut alle Layout-Systeme stoßen darauf und wird als Fehlen einer Lösung bezeichnet .

Es gibt nicht so viele Auswege aus dieser Situation:

• Sie können fallen - dies ist eine sehr häufige Methode. Diejenigen, die mit MacOS arbeiten, wissen, dass NSLayoutConstraintManager genau das tut.
• Gibt den Standardwert zurück . Im Kontext des Layouts können wir immer alle Nullen zurückgeben.
• Eine bekanntere und heikelere Methode besteht darin, falsche Eingaben zu verhindern . Diese Methode wird von gängigen Layoutsystemen verwendet, z. B. Yoga , bekannt als Flex Layout . Solche Systeme versuchen, eine Schnittstelle zu erstellen, die keine falschen Eingaben zulässt.
• Es gibt einen anderen Weg, um absolut alle Probleme zu lösen - alles von Anfang an zu überdenken und zunächst das Auftreten dieses Problems zu verhindern . Auto Layout ging diesen Weg.

Automatisches Layout Erklärung und Lösung des Problems

Wir haben ein rechteckiges Bild und um es eindeutig zu identifizieren, benötigen wir 4 Parameter:

• Koordinaten der oberen linken Ecke;
• Breite und Höhe.

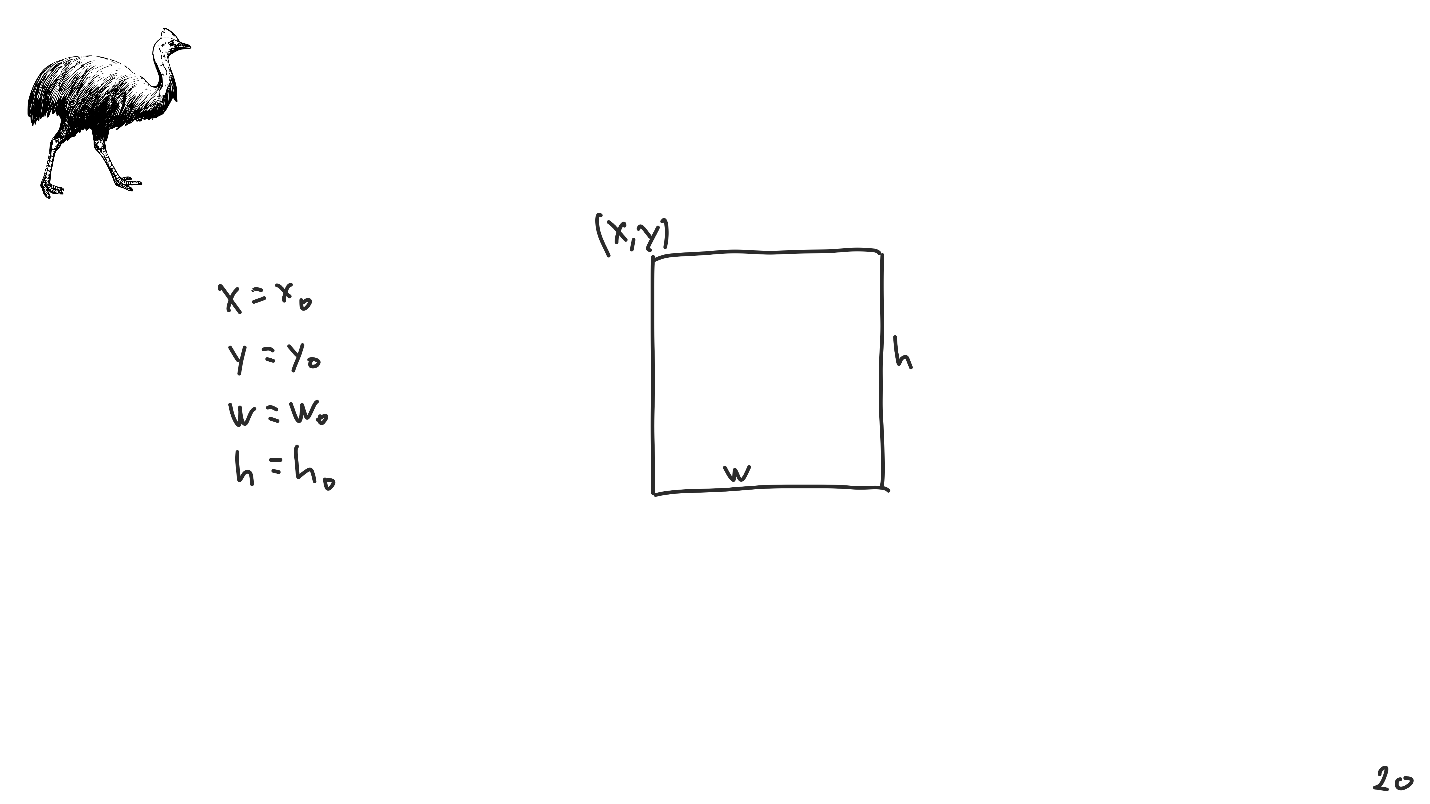
Auto Layout ist sehr ausführlich. Im Vergleich zu einem linearen Gleichungssystem ist es viel schwieriger, alles damit auf dem Bildschirm zu platzieren. Daher werden wir den eindimensionalen Fall ohne Verlust der Allgemeinheit betrachten.



Alles ist sehr einfach: Der Raum ist eine gerade Linie, und alle Objekte, die darin platziert werden können, sind Punkte auf einer geraden Linie. Ein Wert: X = X _P reicht aus, um die Position des Punktes zu bestimmen.

Betrachten Sie den Ansatz des automatischen Layouts. Es gibt einen Bereich, in dem Einschränkungen festgelegt werden. Die Lösung, die wir bekommen wollen, ist X = X ₀ und keine andere.

Es gibt ein Problem - wir haben keine Operationen mit Einschränkungen definiert. Wir können nicht direkt aus dem Datensatz schließen, dass X = X _{0 ist} , wir können nichts multiplizieren oder irgendetwas hinzufügen. Dazu müssen wir die Einschränkung in das umwandeln, mit dem wir arbeiten können - in ein System von Gleichungen und Ungleichungen.



Auto Layout transformiert ein System von Gleichungen und Ungleichungen wie folgt.

• Zunächst werden zwei zusätzliche Variablen eingeführt, die nicht negativ sind und voneinander abhängen . Mindestens einer von ihnen ist gleich Null.
• Die Einschränkung selbst wird in die Notation X = X ₀ + a ⁺ - a ^- konvertiert.

Punkt X ₀   - Lösung des Systems: Wenn a ⁺ und a ^- gleich Null sind, ist dies wahr. Aber jeder andere Punkt auf dieser Linie wird eine Lösung sein.

Daher ist es notwendig, das Beste aus der ganzen Reihe von Lösungen zu finden. Zu diesem Zweck führen wir eine Funktion ein - eine gewöhnliche Funktion, die eine Zahl zurückgibt, und wir können Zahlen vergleichen. Wir zeichnen ein Diagramm und stellen fest, dass die Lösung, die wir ursprünglich erhalten wollten, ein Minimum ist.

Ich habe ein lineares Programmierproblem . Genau das macht Auto Layout mit Einschränkungen, die nicht nur in Form von Gleichheiten, sondern auch in Form von Ungleichungen vorliegen.

Ungleichheitsbeschränkungen

Bei Ungleichheitsbeschränkungen erfolgt die Transformation auf die gleiche Weise wie bei Gleichheiten: Zwei zusätzliche Variablen werden eingeführt und all dies wird im System gesammelt. Nur die Funktion ist unterschiedlich und gleich a ^- .



Die obige Grafik zeigt, warum dies so ist - jeder Wert von a ⁺ mit a ^- = 0 (von X ₀ bis + ∞ ) ist die optimale Lösung für das Problem.

Versuchen wir, diese beiden Einschränkungen von Gleichungen und Ungleichungen zu einer zu kombinieren. Da die Einschränkungen nicht isoliert leben, werden sie zusammen auf das gesamte System angewendet.



Für jede Einschränkung wird ein zusätzliches Variablenpaar eingeführt und die Funktion kompiliert. Da wir möchten, dass alle diese Einschränkungen gleichzeitig erfüllt werden, ist die Funktion gleich der Summe aller Funktionen aus jeder Einschränkung .

Wir sammeln die Funktion f und sehen, dass die Lösung X _{1 ist} . Wie wir erwartet hatten, Einschränkungen. Wir kommen also zum dritten Algorithmus.

Algorithmus Nr. 3

Um etwas zu tun, brauchen Sie:

• ein System linearer Einschränkungen erstellen;
• verwandeln Sie es in ein lineares Programmierproblem;
• Lösen Sie das Problem auf eine bekannte Weise, z. B. die Simplex-Methode , die im automatischen Layout verwendet wird.
• Wenden Sie die Lösung auf UIView an.

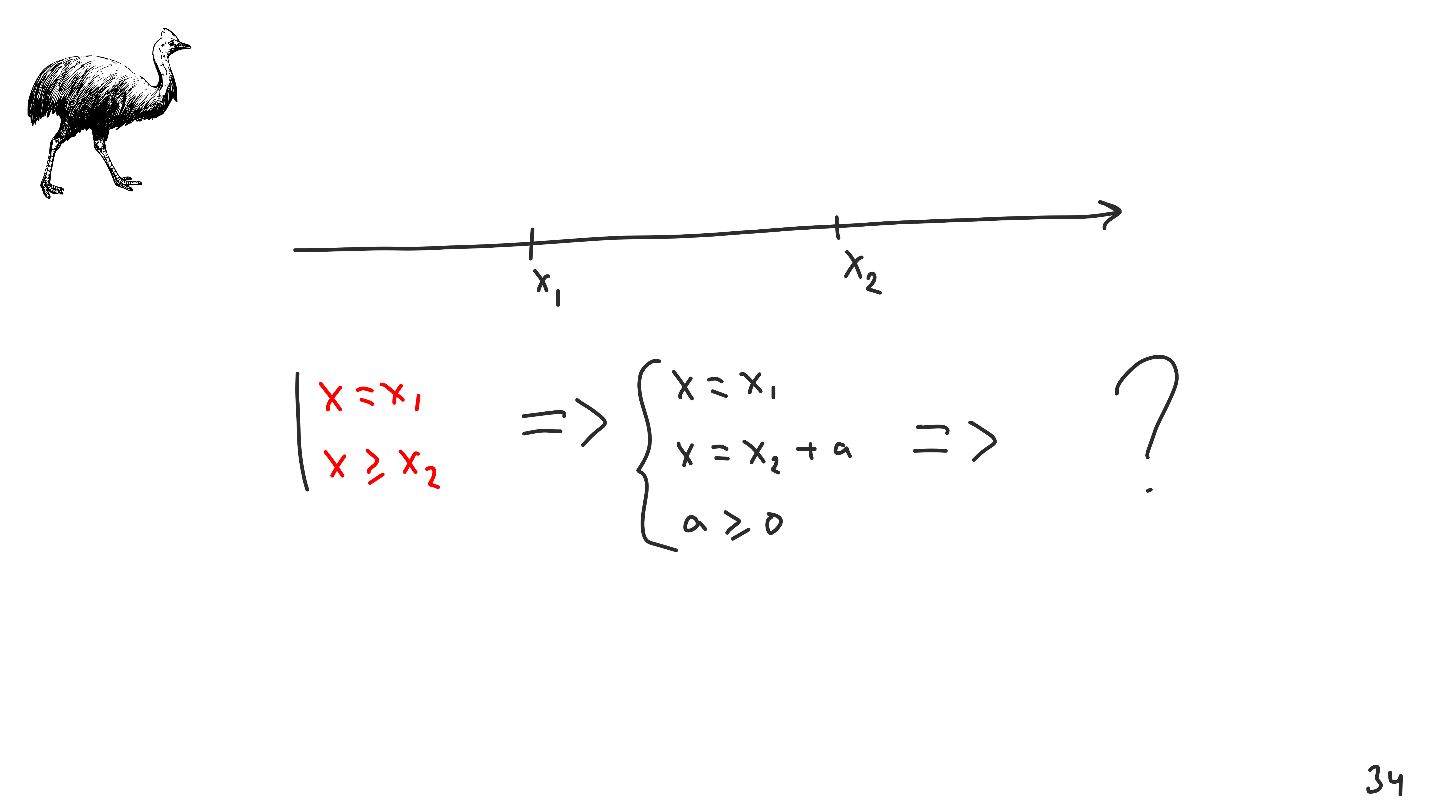
Dieser Algorithmus scheint ausreichend zu sein, aber betrachten Sie den folgenden Fall: Wir ändern den anfänglichen Satz von Einschränkungen so, dass die zweite Einschränkung jetzt X ≥ X _{2 ist} .



Welche Lösung erwarten wir?

• X ₁ ? In der Tat wird in der ersten Einschränkung so geschrieben: X = X ₁ , und diese Lösung widerspricht der zweiten Einschränkung.
• X ₂ ? Es wird bereits einen Konflikt mit der ersten Einschränkung geben.

Um aus der Situation herauszukommen, werden wir Transformationen durchführen, die wir bereits zu tun wissen.

Das Diagramm der neuen Funktionalität sieht anders aus: Jeder Punkt aus dem Intervall von X ₁ bis X ₂ ist die richtige gültige Lösung des Systems. Dies nennt man Unsicherheit .

Unsicherheit

Auto Layout verfügt über einen Mechanismus zur Lösung solcher Probleme - Prioritäten . Ich erinnere Sie daran, dass Gelb eine hohe Priorität und Blau eine niedrige Priorität anzeigt.



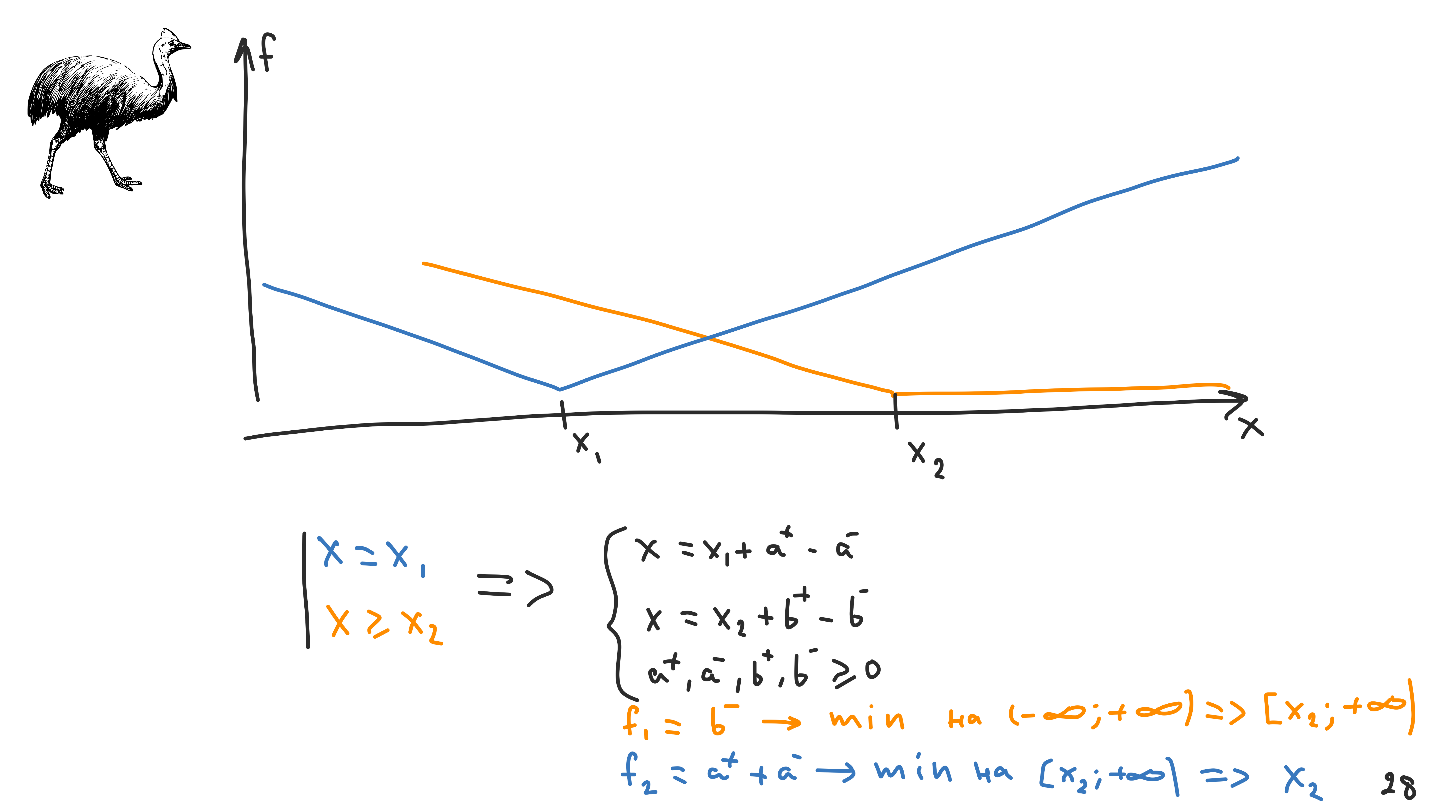
Einschränkungen konvertieren. Bitte beachten Sie, dass das resultierende System nur schwarz ist. Wir wissen, wie man damit arbeitet, und es gibt keine Informationen über Einschränkungen. Es liegt in den Funktionen, von denen es zwei geben wird. Das automatische Layout minimiert zuerst das erste und dann das zweite.

Bei linearen Programmierproblemen suchen wir nicht nach der Lösung selbst, sondern nach einer Reihe praktikabler Lösungen. Natürlich soll dieser Bereich nur ein Punkt sein, und das automatische Layout verhält sich genauso. Erstens minimiert es die Funktion mit der höchsten Priorität für ( - ∞, + ∞) und erhält am Ausgang eine Domäne möglicher Lösungen. Das automatische Layout löst das zweite lineare Programmierproblem bereits im erhaltenen Bereich zulässiger Werte. Ein solcher Mechanismus wird als Hierarchie von Einschränkungen bezeichnet und ergibt in diesem Problem den Punkt X ₂ .

Algorithmus Nr. 4

• Erstellen Sie eine Hierarchie linearer Einschränkungen.
• verwandeln Sie es in eine lineare Programmieraufgabe;
• Lösen Sie nacheinander das Problem der linearen Programmierung - von der höchsten zur niedrigsten Priorität.
• Wenden Sie die Lösung auf UlView an.

Schauen wir uns noch einmal die vorherige Aufgabe an. Wir sind keine Mathematiker, sondern Ingenieure, und jeder Ingenieur sollte hier verwirrt sein.

Hier gibt es ein ernstes Problem - Unendlichkeit , und ich weiß nicht, was es ist.

Der Cassowary-Algorithmus unter der Haube von Auto Layout war kein vorhandener Mechanismus, der bequemerweise auf die Aufgabe Auto Layout fiel, sondern als Layout-Tool gedacht war, und er bot zu Beginn spezielle Mechanismen, um der Unendlichkeit zu entkommen. Hierzu wurden verschiedene Arten von Beschränkungen erfunden:

• Parameter sind die Einschränkungen, mit denen wir gearbeitet haben. Sie werden im Original als Einstellungen bezeichnet, manchmal in der Apple-Dokumentation - optionale Einschränkungen .
• Anforderungen oder Anforderungen - Einschränkungen mit Priorität erforderlich .

Lassen Sie uns sehen, wie Anforderungen mit solchen Prioritäten aus mathematischer Sicht transformiert werden.



Wir haben wieder eine gerade Linie mit zwei Punkten und die erste Einschränkung ist X = X ₁ . Auf der Folie ist es rot, dh diese Einschränkung mit der erforderlichen Priorität - wir nennen es eine Anforderung.

Auto Layout konvertiert es in ein System linearer Gleichungen, das eine Gleichung X = X _{1 enthält} . Nichts mehr - keine linearen Programmieraufgaben, keine Optimierungen.

Ähnlich verhält es sich mit Ungleichungen, die jedoch etwas komplizierter sind. Es wird eine zusätzliche Variable angezeigt, die Werte größer als 0 annehmen kann. Für Werte größer als 0 wird diese Einschränkung erfüllt. Bitte beachten Sie, dass hier keine linearen Programmieraufgaben und Optimierungen vorhanden sind.

Versuchen wir, all dies zu kombinieren, zwei Anforderungen zusammenzustellen und sie in ein System umzuwandeln. Ein aufmerksamer Leser stellte fest, dass wir zu demselben Thema gekommen sind, mit dem wir begonnen haben - die Anforderungen sollten konsistent sein .



Erforderliche Einschränkungen oder Anforderungen sind ein sehr leistungsfähiges Werkzeug, aber nicht das Hauptwerkzeug, sondern das Hilfswerkzeug. Es wurde speziell in Auto Layout eingeführt, um das Problem der unendlichen Intervalle zu lösen. Es muss sorgfältig verwendet werden.

Versuchen wir, alle Arten von Einschränkungen, die wir getroffen haben, in einem System zu kombinieren. Angenommen, wir möchten das Problem nicht auf der gesamten Linie lösen, sondern nur zwischen X ₀ und X ₃ . Wenn wir all dies in ein System linearer Gleichungen und Ungleichungen umwandeln, erhalten wir Folgendes.



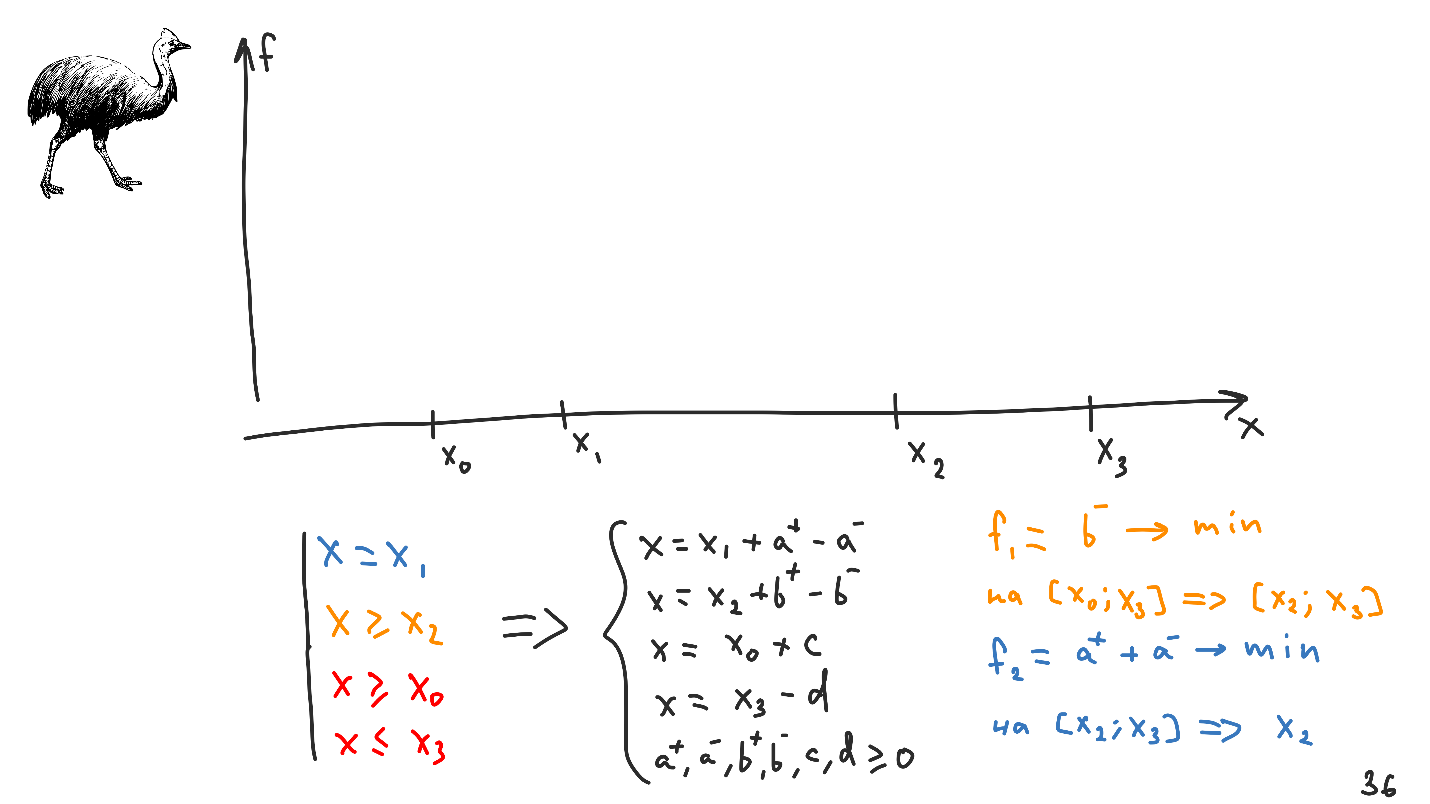
Im Vergleich zum vorherigen System wurden zwei zusätzliche Variablen hinzugefügt - c und d , die jedoch nicht in die Funktionale eingehen, da Einschränkungen des erforderlichen Typs die Funktion in ihrer ursprünglichen Form nicht beeinflussen.

Es scheint, dass sich die Aufgabe nicht wesentlich geändert hat - wir minimieren das gleiche wie zuvor, aber der anfängliche Bereich akzeptabler Werte ändert sich, jetzt ist er von X ₀ bis X ₃ .

Aus mathematischer Sicht sind Anforderungen - Einschränkungen des erforderlichen Typs - die Fähigkeit, zusätzliche Gleichungen in das System einzuführen, ohne dessen Funktionen zu ändern.

Sie müssen dabei sehr vorsichtig sein, da ein übermäßiger Missbrauch der erforderlichen Einschränkungen zu einem Problem ohne Lösungen führt und das automatische Layout damit nicht fertig wird.

Wir kommen zum letzten fünften Algorithmus.

Algorithmus Nr. 5

• Definieren Sie die erforderlichen Einschränkungen - Layoutanforderungen;
• Erstellen Sie eine Hierarchie linearer Einschränkungen.
• alle Einschränkungen in ein lineares Programmierproblem umwandeln;
• das Problem der linearen Programmierung lösen;
• Wenden Sie die Lösung auf UlView an.

Wir haben Cassowary untersucht - einen Algorithmus, der sich innerhalb des automatischen Layouts befindet. Bei seiner Implementierung ergeben sich jedoch verschiedene Funktionen.

IOS-Funktionen

In layoutSubviews () gibt es keine Berechnungen .

Wann werden sie produziert? Antwort: Immer und jederzeit wird das automatische Layout gezählt. Die Berechnung erfolgt genau dann, wenn wir unserer Ansicht Einschränkungen hinzufügen oder diese mithilfe moderner API-Methoden zum Arbeiten mit Einschränkungen aktivieren.



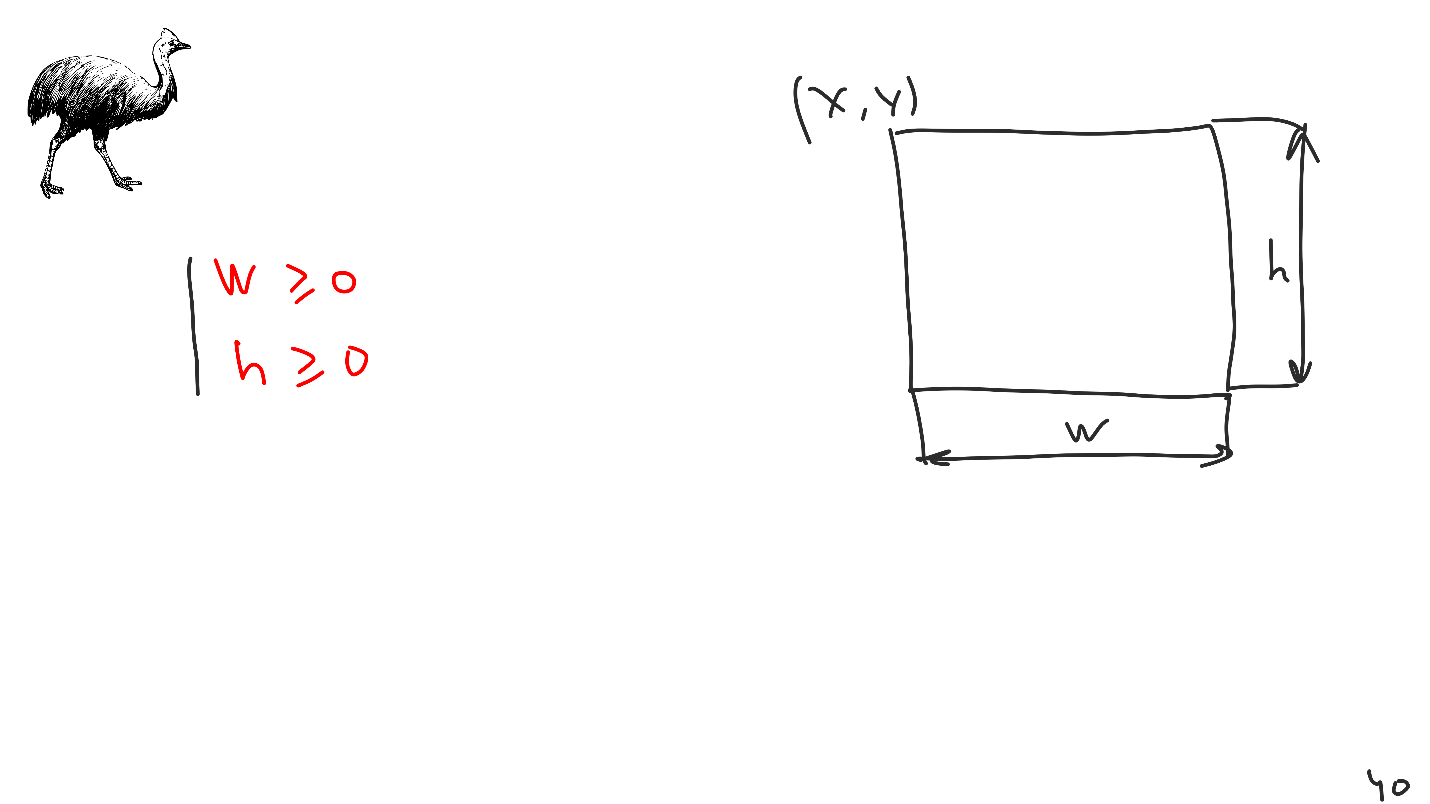
Unsere Ansichten sind Rechtecke, aber das Problem ist, dass diese Informationen nicht im Cassowary enthalten sind, sondern zusätzlich dort eingebettet werden müssen. Wir haben einen Mechanismus zur Einführung zusätzlicher Einschränkungen. Wenn wir für jede Ansicht eine Reihe von Einschränkungen mit positiver Breite und Höhe einführen, erhalten wir am Ausgang immer Rechtecke. Aus diesem Grund können wir die automatische Layoutansicht mit negativen Abmessungen nicht nachholen.

Die zweite Funktion ist intrinsicContentSize - die intrinsische Größe, die für jede Ansicht festgelegt werden kann.



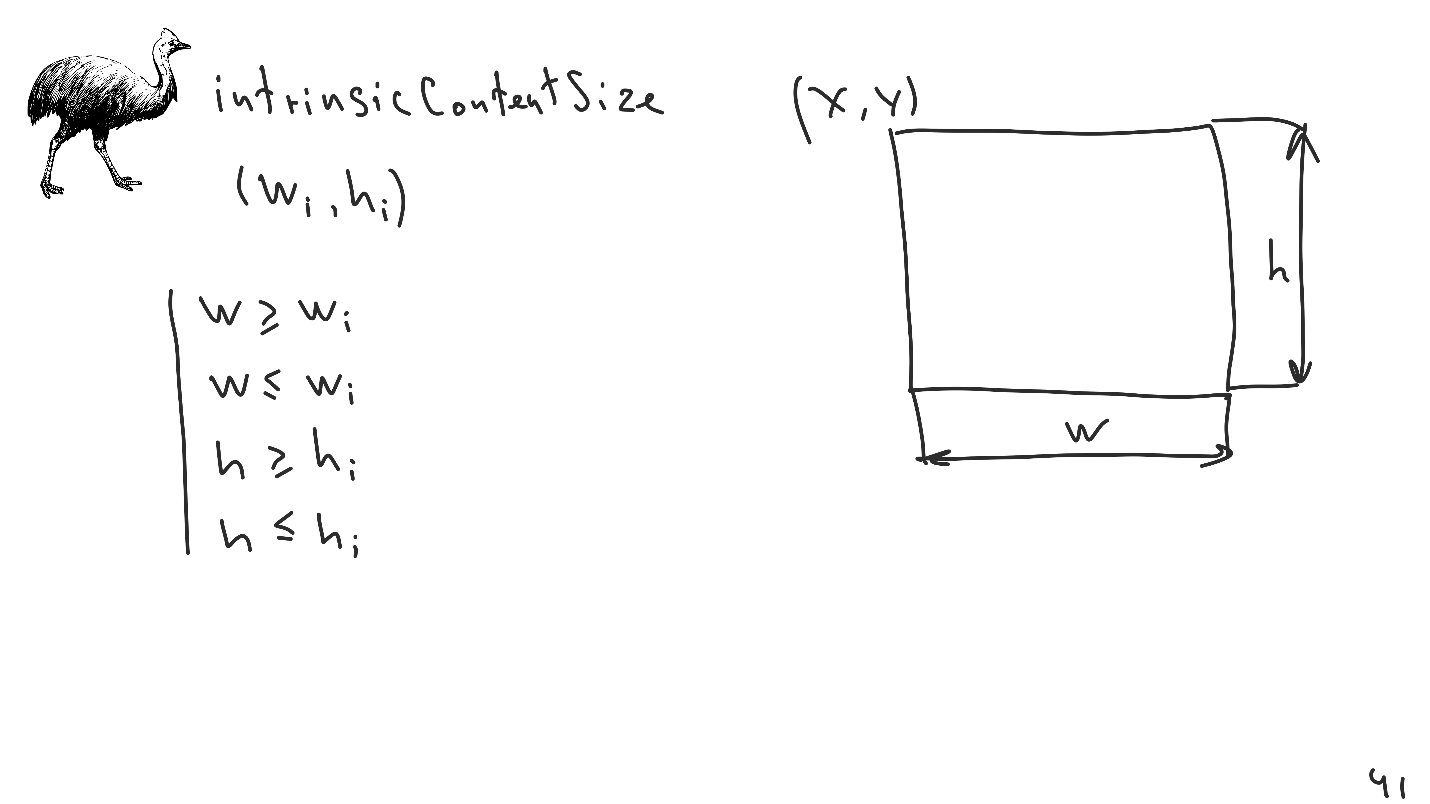
Dies ist eine einfache Schnittstelle zum Erstellen von 4 zusätzlichen Ungleichheitsbeschränkungen, die in das System eingefügt werden. Dieser Mechanismus ist sehr praktisch und ermöglicht es Ihnen, die Anzahl der expliziten Einschränkungen zu reduzieren, was die Verwendung des automatischen Layouts vereinfacht. Der letzte und dünnste Punkt, der oft vergessen wird, ist TranslateAutoresizingMaskIntoConstraints.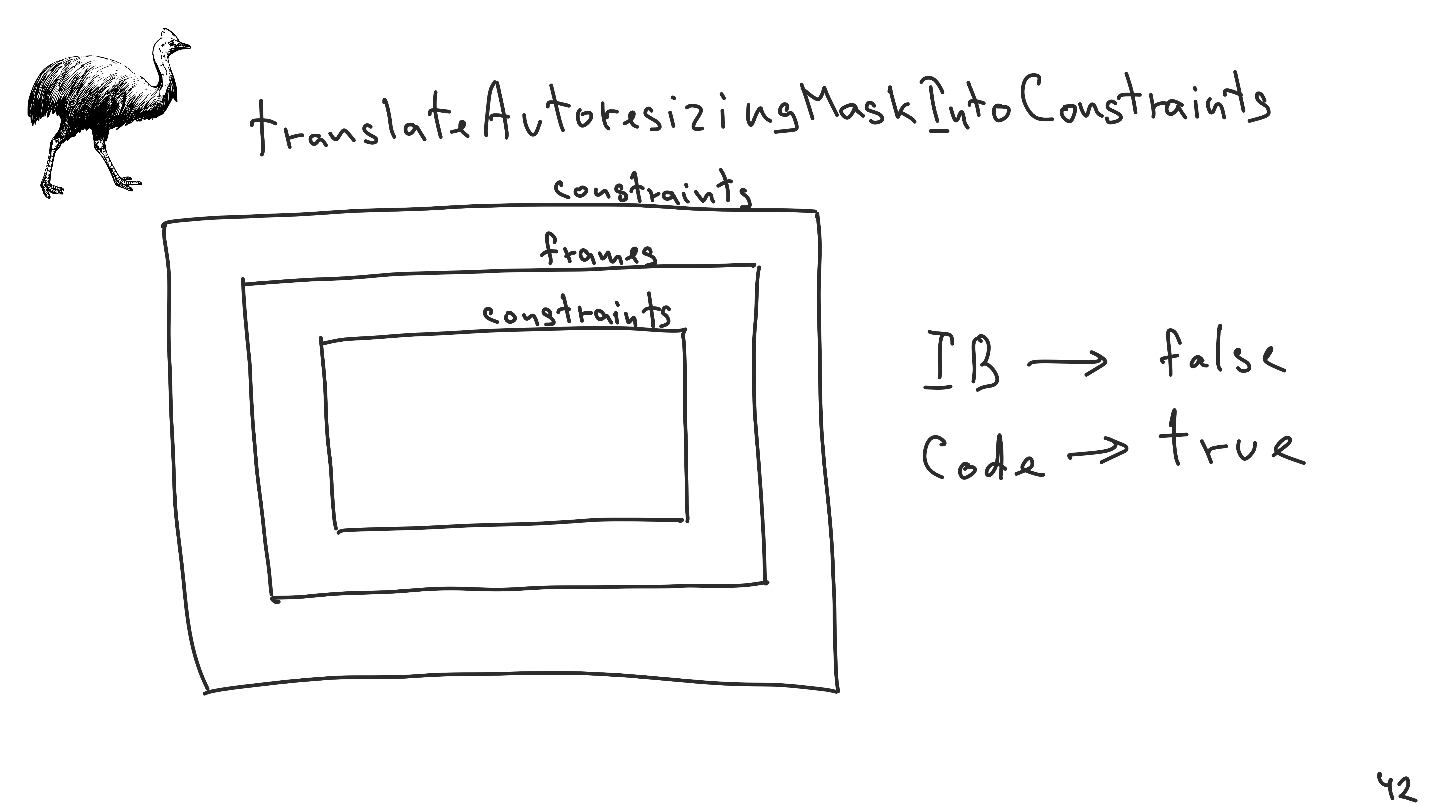



Dies ist eine Krücke, die in den Tagen von iOS 5 eingeführt wurde, damit der alte Code nach dem Erscheinen von Auto Layout nicht kaputt geht.

Stellen Sie sich eine Situation vor: Wir legen Einschränkungen fest. Innerhalb der Ansicht verwenden wir die Ansicht, die nichts über Einschränkungen weiß, alles, was auf Frames gesetzt ist, aber innerhalb der Ansicht die Ansicht, die seit langem in Einschränkungen übersetzt wurde.

Ich erinnere Sie daran, dass in der Auto-Layout-Aufgabe von Cassowary keine Frames enthalten sind, sondern nur Einschränkungen.

Die Größe und Position der Ansicht, die in den Frames reduziert wurde, wird durch Einschränkungen nicht vollständig bestimmt. Bei der Berechnung der Größe und Position aller anderen Ansichten werden falsche Größen berücksichtigt, obwohl wir nach dem automatischen Layout dort die richtigen Rahmen anwenden.

Um diese Situation zu vermeiden, wird für jede Ansicht, die im Frame angeordnet ist, eine zusätzliche Einschränkung angewendet, wenn der Wert der Variablen TranslateAutoresizingMaskIntoConstraints true ist. Diese Einschränkungen können von Lauf zu Lauf variieren. Über dieses Set ist nur eines bekannt - sein Rahmen wird derjenige sein, der übertragen wurde.

Die Kompatibilität zwischen altem Code ohne Einschränkungen und neuem Code mit Einschränkungen kann häufig durch den Missbrauch dieser Eigenschaft beeinträchtigt werden. Diese Einschränkungen haben notwendigerweise die Priorität von Anforderungen. Wenn wir also einer solchen Ansicht, die eine sehr hohe Priorität hat, beispielsweise einer Anforderung, plötzlich Einschränkungen auferlegen, können wir versehentlich ein nicht konsistentes System erstellen, das keine Lösungen hat.

Es ist wichtig zu wissen:

• Wenn wir eine Ansicht aus dem Interface Builder erstellen, ist der Standardwert für diese Eigenschaft false .
• Wenn wir eine Ansicht direkt aus dem Code erstellen, ist dies der Fall .

Die Idee ist sehr einfach: Der alte Code, in dem die Ansicht erstellt wurde, wusste nichts über das automatische Layout, und es musste so gestaltet werden, dass es funktioniert, wenn die Ansicht irgendwo an einem neuen Ort verwendet wird.

Praktische Tipps

Insgesamt wird es drei Räte geben, die mit den wichtigsten beginnen.

Optimierung

Es ist wichtig, das Problem zu lokalisieren.

Haben Sie jemals das Problem der Optimierung des Bildschirms gehabt, der im automatischen Layout dargestellt ist? Höchstwahrscheinlich nicht, häufiger hatten Sie das Problem, das Layout von Zellen in einer Tabelle oder einer Sammlungsansicht zu optimieren.

Das automatische Layout ist so optimiert, dass jeder Bildschirm und jede Benutzeroberfläche erstellt werden kann. Es ist jedoch ein Problem, 50 oder 100 gleichzeitig zu erstellen. Schauen wir uns das Experiment an, um es zu lokalisieren und zu optimieren. Die Zahlen stammen aus einem Artikel, in dem Cassowary erstmals beschrieben wurde.


Die Aufgabe ist folgende: Wir erstellen nacheinander eine Ansichtskette und verbinden jede nachfolgende mit der vorherigen. So wurde eine Folge von 1000 Elementen erstellt. Nach dem Messen verschiedener Operationen wird die Zeit in Millisekunden angezeigt. Die Werte sind ziemlich groß, da Auto Layout an der Kreuzung der 80er und 90er Jahre erfunden wurde.

Durch das Sammeln einer solchen Kette können Sie wie folgt vorgehen:

• Fügen Sie nacheinander eine Einschränkung hinzu und entscheiden Sie jedes Mal. Dies dauert 38 Sekunden.
• Sie können alle Einschränkungen auf einmal hinzufügen und erst dann das System lösen. Diese Lösung ist effizienter. Nach alten Daten steigt der Wirkungsgrad um 70%, bei der derzeitigen Implementierung auf modernen Geräten werden es jedoch nur 20% sein. Eine qualitativ einmalige Hinzufügung von Beschränkungen wird jedoch immer effektiver sein.
• Wenn die gesamte Kette zusammengebaut ist, können Sie eine weitere Einschränkung hinzufügen . Wie aus der Tabelle ersichtlich ist, ist diese Operation ziemlich billig.
• Das Interessanteste: Wenn wir keine neuen Einschränkungen hinzufügen, sondern eine Konstante in einer der vorhandenen ändern, ist dies eine Größenordnung effektiver als das Löschen oder Erstellen einer neuen Einschränkung.

Die ersten beiden Punkte können als primäre Berechnung der Schnittstellen beschrieben werden, die letzten beiden - als nächste.

Berechnung der primären Schnittstelle

Hier können Sie die Methoden zum Hinzufügen von Masseneinschränkungen zur Optimierung verwenden:

• NSLayoutConstraints.activate (_ :) - Sammeln Sie beim Erstellen einer Ansicht alle Einschränkungen nacheinander in einem Array, zwischenspeichern Sie sie und fügen Sie sie erst dann hinzu.
• Oder erstellen Sie Zellen im Interface Builder. Er wird alles für uns tun und zusätzliche Optimierungen durchführen, was oft bequem ist.

Nachfolgende Schnittstellenberechnungen

Das Hinzufügen oder Ändern von Einschränkungen ist eine komplexe Operation. Es ist daher besser , die Einschränkungen nicht zu ändern, sondern nur die Konstanten in vorhandenen Einschränkungen zu ändern . :

• UIView — . view , Auto Layout. , , view, .
• — IntrinsicContentSize. , , .
• . , , .

, WWDC 2018S220 High Performance Auto Layout . — Apple , .

, constraints.

required , — , , . .

, .

:

• , . ( loader) — .
• , . , .

, , .

constraint required, . , , , . , .

— , . , — . - , , . Auto Layout , .

, . . , , , . layout, , , . .

— , Auto Layout, , .

, required, , . :

• , .
• , , .

, , , .

, . , , , . , — . .

— . , , , — , — required -.

Nützliche Links:

Solving Linear Arithmetic Constraints for User Interface Applications
The Cassowary Linear Constraint Solving Algorithm
Constraints as s Design Pattern
Auto Layout Guide by Apple
WWDC 2018 Session 220 High Performance Auto Layout
UILabel API Auto Layout —
. Medium

, AppsConf 2019 . , AppsConf , 22 23 . - , .