Einführung

Als wir das letzte Mal über OSG-spezifische Programmiertechniken sprachen, sprachen wir über den Callback-Mechanismus und seine Implementierung in der Engine. Es ist an der Zeit, die Möglichkeiten zu untersuchen, die dieser Mechanismus für die Verwaltung des Inhalts einer dreidimensionalen Szene bietet.

Wenn wir über Objektanimation sprechen, bietet OSG dem Entwickler zwei Optionen für seine Implementierung:

1. Prozedurale Animation, die programmgesteuert durch die Transformation von Objekten und ihren Attributen implementiert wird
2. Exportieren von Animationen aus einem 3D-Editor und Verwalten aus Anwendungscode

Betrachten Sie zunächst die erste Möglichkeit als die offensichtlichste. Wir werden auf jeden Fall etwas später über die Sekunde sprechen.

1. Prozedurale Morphing-Animation

Beim Durchlaufen des Szenendiagramms überträgt OSG Daten an die OpenGL-Pipeline, die in einem separaten Thread ausgeführt wird. Dieser Thread muss mit anderen Verarbeitungsthreads in jedem Frame synchronisiert werden. Andernfalls kann die Methode frame () abgeschlossen werden, bevor Geometriedaten verarbeitet werden. Dies führt zu unvorhersehbarem Programmverhalten und Abstürzen. OSG bietet eine Lösung für dieses Problem in Form der setDataVariance () -Methode der osg :: Object-Klasse, die die Basis für alle Szenenobjekte darstellt. Sie können drei Verarbeitungsmodi für Objekte einstellen

1. NICHT SPEZIFIZIERT (standardmäßig) - OSG bestimmt unabhängig die Verarbeitungsreihenfolge des Objekts.
   
2. STATISCH - Das Objekt ist unveränderlich und die Reihenfolge seiner Verarbeitung ist nicht wichtig. Beschleunigt das Rendern erheblich.
   
3. DYNAMISCH - Das Objekt muss vor dem Start des Renderns verarbeitet werden.
   

Diese Einstellung kann jederzeit per Anruf vorgenommen werden

node->setDataVariance( osg::Object::DYNAMIC ); 

Die allgemein akzeptierte Praxis besteht darin, die Geometrie "on the fly" zu ändern, dh die Koordinaten von Scheitelpunkten, Farbnormalen und Texturen in jedem Rahmen dynamisch zu ändern, um veränderbare Geometrie zu erhalten. Diese Technik wird als Morphing-Animation bezeichnet. In diesem Fall ist die Reihenfolge der Verarbeitung der Geometrie entscheidend - alle Änderungen müssen vor Beginn des Zeichnens neu berechnet werden. Um diesen Trick zu veranschaulichen, ändern wir das Beispiel für farbige Quadrate geringfügig und zwingen einen seiner Scheitelpunkte, sich um die X-Achse zu drehen.


Wir werden ein Quadrat in einer separaten Funktion erstellen

 osg::Geometry *createQuad() { osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array; vertices->push_back( osg::Vec3(0.0f, 0.0f, 0.0f) ); vertices->push_back( osg::Vec3(1.0f, 0.0f, 0.0f) ); vertices->push_back( osg::Vec3(1.0f, 0.0f, 1.0f) ); vertices->push_back( osg::Vec3(0.0f, 0.0f, 1.0f) ); osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array; normals->push_back( osg::Vec3(0.0f, -1.0f, 0.0f) ); osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array; colors->push_back( osg::Vec4(1.0f, 0.0f, 0.0f, 1.0f) ); colors->push_back( osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f) ); colors->push_back( osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f) ); colors->push_back( osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f) ); osg::ref_ptr<osg::Geometry> quad = new osg::Geometry; quad->setVertexArray(vertices.get()); quad->setNormalArray(normals.get()); quad->setNormalBinding(osg::Geometry::BIND_OVERALL); quad->setColorArray(colors.get()); quad->setColorBinding(osg::Geometry::BIND_PER_VERTEX); quad->addPrimitiveSet(new osg::DrawArrays(GL_QUADS, 0, 4)); return quad.release(); } 

Eine Beschreibung davon ist grundsätzlich nicht erforderlich, da wir solche Maßnahmen wiederholt durchgeführt haben. Um die Eckpunkte dieses Quadrats zu ändern, schreiben wir die DynamicQuadCallback-Klasse und erben sie von osg :: Drawable :: UpdateCallback

 class DynamicQuadCallback : public osg::Drawable::UpdateCallback { public: virtual void update(osg::NodeVisitor *, osg::Drawable *drawable); }; 

Überschreiben der update () -Methode darin

 void DynamicQuadCallback::update(osg::NodeVisitor *, osg::Drawable *drawable) { osg::Geometry *quad = static_cast<osg::Geometry *>(drawable); if (!quad) return; osg::Vec3Array *vertices = static_cast<osg::Vec3Array *>(quad->getVertexArray()); if (!vertices) return; osg::Quat quat(osg::PI * 0.01, osg::X_AXIS); vertices->back() = quat * vertices->back(); quad->dirtyDisplayList(); quad->dirtyBound(); } 

Hier erhalten wir einen Zeiger auf ein Geometrieobjekt

 osg::Geometry *quad = static_cast<osg::Geometry *>(drawable); 

wir lesen aus der Geometrie eine Liste von Eckpunkten (oder vielmehr einen Zeiger darauf)

 osg::Vec3Array *vertices = static_cast<osg::Vec3Array *>(quad->getVertexArray()); 

Um das letzte Element (den letzten Scheitelpunkt) im Array abzurufen, stellt die Klasse osg :: Array die Methode back () bereit. Um die Drehung des Scheitelpunkts relativ zur X-Achse durchzuführen, führen wir die Quaternion ein

 osg::Quat quat(osg::PI * 0.01, osg::X_AXIS); 

Das heißt, wir setzen eine Quaternion, die eine Drehung um die X-Achse um einen Winkel von 0,01 * Pi implementiert. Drehen Sie den Scheitelpunkt, indem Sie das Quaternion mit einem Vektor multiplizieren, der die Koordinaten des Scheitelpunkts definiert

 vertices->back() = quat * vertices->back(); 

Die letzten beiden Aufrufe enthalten die Anzeigeliste und das dimensionale Parallelepiped für die geänderte Geometrie

 quad->dirtyDisplayList(); quad->dirtyBound(); 

Im Hauptteil der main () -Funktion erstellen wir ein Quadrat, legen den dynamischen Zeichenmodus dafür fest und fügen einen Rückruf hinzu, der die Geometrie ändert

 osg::Geometry *quad = createQuad(); quad->setDataVariance(osg::Object::DYNAMIC); quad->setUpdateCallback(new DynamicQuadCallback); 

Ich werde den Stammknoten wahllos erstellen und den Viewer starten, da wir dies bereits mindestens zwanzig Mal auf unterschiedliche Weise getan haben. Als Ergebnis haben wir die einfachste Morphing-Animation



Versuchen Sie nun, den Aufruf setDataVariance () zu entfernen (zu kommentieren). Vielleicht sehen wir in diesem Fall nichts Kriminelles - standardmäßig versucht OSG automatisch zu bestimmen, wann Geometriedaten aktualisiert werden sollen, und versucht, mit dem Rendern zu synchronisieren. Versuchen Sie dann, den Modus von DYNAMISCH auf STATISCH zu ändern, und Sie werden feststellen, dass das Bild nicht reibungslos gerendert wird und spürbare Rucke, Fehler und Warnungen wie diese in die Konsole gelangen

 Warning: detected OpenGL error 'invalid value' at after RenderBin::draw(..) 

Wenn Sie die Methode dirtyDisplayList () nicht ausführen, ignoriert OpenGL alle Änderungen an der Geometrie und verwendet die am Anfang erstellte Anzeigeliste, um das Quadrat für das Rendern zu erstellen. Löschen Sie diesen Anruf und Sie werden sehen, dass es keine Animation gibt.

Ohne den Aufruf der Methode dirtyBound () wird der Begrenzungsrahmen nicht neu berechnet und OSG schneidet unsichtbare Flächen falsch ab.

2. Das Konzept der Bewegungsinterpolation

Angenommen, ein Zug von Station A nach Station B benötigt 15 Minuten. Wie können wir diese Situation simulieren, indem wir die Position des Zuges im Rückruf ändern? Am einfachsten ist es, die Position von Station A mit der Zeit 0 und Station B mit 15 Minuten zu korrelieren und den Zug gleichmäßig zwischen diesen Zeiten zu bewegen. Dieser einfachste Ansatz wird als lineare Interpolation bezeichnet. Bei der linearen Interpolation wird ein Vektor, der die Position eines Zwischenpunkts angibt, durch die Formel beschrieben

 p = (1 - t) * p0 + t * p1 

wobei p0 der Ausgangspunkt ist; p1 ist der Endpunkt; t ist ein Parameter, der gleichmäßig von 0 bis 1 variiert. Die Bewegung des Zuges ist jedoch viel komplizierter: Er verlässt die Station A, beschleunigt, bewegt sich dann mit konstanter Geschwindigkeit und verlangsamt sich, stoppt an Station B. Ein solcher Prozess kann die lineare Interpolation und nicht mehr beschreiben Es sieht unnatürlich aus.

OSG stellt dem Entwickler die osgAnimation-Bibliothek zur Verfügung, die eine Reihe von Standardinterpolationsalgorithmen enthält, mit denen die Bewegung von Szenenobjekten reibungslos animiert werden kann. Jede dieser Funktionen hat normalerweise zwei Argumente: den Anfangswert des Parameters (normalerweise 0) und den Endwert des Parameters (normalerweise 1). Diese Funktionen können auf den Beginn der Bewegung (InMotion), auf das Ende der Bewegung (OutMotion) oder auf den Beginn und das Ende der Bewegung (InOutMotion) angewendet werden.

Art der Bewegung	in der Klasse	aus der Klasse	In / Out-Klasse
Lineare Interpolation	LinearMotion	- -	- -
Quadratische Interpolation	InQuadMotion	OutQuadMotion	InOutQuadMotion
Kubische Interpolation	InCubicMotion	Outcubicmotion	InOutCubicMotion
Interpolation 4-Ordnung	InQuartMotion	OutQuartMotion	InOutQuartMotion
Bounce-Effekt-Interpolation	InBounceMotion	OutBounceMotion	InOutBounceMotion
Elastische Rückprallinterpolation	InElasticMotion	OutElasticMotion	InOutElasticMotion
Sinusinterpolation	InSineMotion	Outsinemotion	InOutSineMotion
Inverse Interpolation	Inbackmotion	Outbackmotion	InOutBackMotion
Kreisinterpolation	InCircMotion	Outcircmotion	InOutCircMotion
Exponentielle Interpolation	InExpoMotion	Outexpomotion	InOutExpoMotion

Um eine lineare Interpolation der Bewegung eines Objekts zu erstellen, schreiben wir einen solchen Code

 osg::ref_ptr<osgAnimation::LinearMotion> motion = new osgAnimation::LinearMotion(0.0f, 1.0f); 

3. Animation von Transformationsknoten

Trajektorienanimation ist die häufigste Art von Animation in Grafikanwendungen. Diese Technik kann verwendet werden, um die Bewegung eines Autos, den Flug eines Flugzeugs oder die Bewegung der Kamera zu animieren. Die Flugbahn ist vordefiniert, wobei alle Positionen, Rotationen und Skalenänderungen zu Schlüsselzeitpunkten vorgenommen werden. Wenn der Simulationszyklus beginnt, wird der Zustand des Objekts in jedem Rahmen unter Verwendung einer linearen Interpolation für Position und Skalierung und einer sphärischen linearen Interpolation für Rotationsquaternionen neu berechnet. Hierfür wird die interne Methode slerp () der Klasse osg :: Quat verwendet.

OSG bietet die Klasse osg :: AnimationPath, um einen zeitlich variierenden Pfad zu beschreiben. Die Methode dieser Klasse insert () wird verwendet, um Kontrollpunkte, die bestimmten Zeitpunkten entsprechen, zur Trajektorie hinzuzufügen. Der Kontrollpunkt wird durch die Klasse osg :: AnimationPath :: ControlPoint beschrieben, deren Konstruktor die Position als Parameter und optional die Parameter für Objektrotation und Skalierung verwendet. Zum Beispiel

 osg::ref_ptr<osg::AnimationPath> path = new osg::AnimationPath; path->insert(t1, osg::AnimationPath::ControlPoint(pos1, rot1, scale1)); path->insert(t2, ...); 

Hier sind t1, t2 Zeitpunkte in Sekunden; rot1 ist der Rotationsparameter zum Zeitpunkt t1, der durch die Quaternion osg :: Quat beschrieben wird.

Es ist möglich, Animationsschleifen über die setLoopMode () -Methode zu steuern. Standardmäßig ist der LOOP-Modus aktiviert - die Animation wird kontinuierlich wiederholt. Andere mögliche Werte: NO_LOOPING - Animation einmal abspielen und SWING - Schleife der Bewegung in Vorwärts- und Rückwärtsrichtung.

Nachdem alle Initialisierungen abgeschlossen sind, hängen wir das Objekt osg :: AnimationPath an das integrierte Objekt osg :: AnimationPathCallback an, das von der Klasse osg :: NodeCallback abgeleitet ist.

4. Ein Beispiel für eine Animation der Bewegung entlang eines Pfades

Jetzt bewegen wir unsere Cessna in einem Kreis mit dem Mittelpunkt am Punkt (0,0,0). Die Position des Flugzeugs auf der Flugbahn wird durch lineare Interpolation der Position und Ausrichtung zwischen Schlüsselbildern berechnet.


Wir beginnen mit der Erstellung der Flugbahn des Flugzeugs und nehmen diesen Code in eine separate Funktion auf

 osg::AnimationPath *createAnimationPath(double radius, double time) { osg::ref_ptr<osg::AnimationPath> path = new osg::AnimationPath; path->setLoopMode(osg::AnimationPath::LOOP); unsigned int numSamples = 32; double delta_yaw = 2.0 * osg::PI / (static_cast<double>(numSamples) - 1.0); double delta_time = time / static_cast<double>(numSamples); for (unsigned int i = 0; i < numSamples; ++i) { double yaw = delta_yaw * i; osg::Vec3d pos(radius * sin(yaw), radius * cos(yaw), 0.0); osg::Quat rot(-yaw, osg::Z_AXIS); path->insert(delta_time * i, osg::AnimationPath::ControlPoint(pos, rot)); } return path.release(); } 

Als Parameter nimmt die Funktion den Radius des Kreises, entlang dem sich die Ebene bewegt, und die Zeit, in der sie eine Umdrehung macht. Erstellen Sie innerhalb der Funktion ein Trajektorienobjekt und aktivieren Sie den Animationsschleifenmodus

 osg::ref_ptr<osg::AnimationPath> path = new osg::AnimationPath; path->setLoopMode(osg::AnimationPath::LOOP); 

Folgender Code

 unsigned int numSamples = 32; double delta_yaw = 2.0 * osg::PI / (static_cast<double>(numSamples) - 1.0); double delta_time = time / static_cast<double>(numSamples); 

berechnet die Approximationsparameter der Trajektorie. Wir teilen die gesamte Trajektorie in numSamples von geraden Abschnitten und berechnen die Änderung des Drehwinkels der Ebene um die vertikale Achse (Gieren) delta_yaw und die Änderung der Zeit delta_time beim Übergang von Abschnitt zu Abschnitt. Erstellen Sie nun die erforderlichen Kontrollpunkte

 for (unsigned int i = 0; i < numSamples; ++i) { double yaw = delta_yaw * i; osg::Vec3d pos(radius * sin(yaw), radius * cos(yaw), 0.0); osg::Quat rot(-yaw, osg::Z_AXIS); path->insert(delta_time * i, osg::AnimationPath::ControlPoint(pos, rot)); } 

Im Zyklus werden alle Abschnitte der Flugbahn vom ersten bis zum letzten sortiert. Jeder Kontrollpunkt ist durch einen Gierwinkel gekennzeichnet

 double yaw = delta_yaw * i; 

die Position des Massenschwerpunkts des Flugzeugs im Weltraum

 osg::Vec3d pos(radius * sin(yaw), radius * cos(yaw), 0.0); 

Die Drehung des Flugzeugs zum gewünschten Gierwinkel (relativ zur vertikalen Achse) wird durch das Quaternion eingestellt

 osg::Quat rot(-yaw, osg::Z_AXIS); 

Fügen Sie dann die berechneten Parameter zur Liste der Kontrollpunkte des Pfads hinzu

 path->insert(delta_time * i, osg::AnimationPath::ControlPoint(pos, rot)); 

Im Hauptprogramm achten wir auf die Nuance bei der Angabe des Namens der Flugzeugmodelldatei beim Booten

 osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("../data/cessna.osg.0,0,90.rot"); 

- Dem Dateinamen wurde das Suffix ".0,0,90.rot" hinzugefügt. Mit dem Mechanismus zum Laden der Geometrie aus einer in OSG verwendeten Datei können Sie die Anfangsposition und Ausrichtung des Modells nach dem Laden festlegen. In diesem Fall soll das Modell nach dem Laden um 90 Grad um die Z-Achse gedreht werden.

Als Nächstes wird der Stammknoten erstellt, der der Transformationsknoten ist, und das Modellobjekt wird ihm als untergeordneter Knoten hinzugefügt

 osg::ref_ptr<osg::MatrixTransform> root = new osg::MatrixTransform; root->addChild(model.get()); 

Erstellen Sie nun einen Rückruf für eine Trajektorienanimation und fügen Sie den von der Funktion createAnimationPath () erstellten Pfad hinzu

 osg::ref_ptr<osg::AnimationPathCallback> apcb = new osg::AnimationPathCallback; apcb->setAnimationPath(createAnimationPath(50.0, 6.0)); 

Hängen Sie diesen Rückruf an den Transformationsknoten an

 root->setUpdateCallback(apcb.get()); 

Der Viewer wird wie gewohnt initialisiert und gestartet.

 osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); 

Holen Sie sich eine Flugzeugbewegungsanimation



Denken Sie, Sie haben in diesem Beispiel nichts Seltsames gefunden? Zuvor haben Sie beispielsweise in einem Programm beim Rendern in eine Textur die Transformationsmatrix explizit geändert, um eine Änderung der Position des Modells im Raum zu erzielen. Hier erstellen wir einfach einen Transformationsknoten und im Code gibt es nirgendwo eine explizite Matrixzuweisung.

Das Geheimnis ist, dass die spezielle Klasse osg :: AnimationPathCallback diesen Job erledigt. Entsprechend der aktuellen Position des Objekts auf dem Pfad berechnet es die Transformationsmatrix und wendet sie automatisch auf den Transformationsknoten an, an den es angehängt ist, wodurch der Entwickler vor einer Reihe von Routineoperationen bewahrt wird.

Es ist zu beachten, dass das Anhängen von osg :: AnimationPathCallback an andere Knotentypen nicht nur keine Auswirkungen hat, sondern auch zu undefiniertem Programmverhalten führen kann. Es ist wichtig zu beachten, dass dieser Rückruf nur Transformationsknoten betrifft.

5. Software-Steuerungsanimation

Die osg :: AnimationPathCallback-Klasse bietet Methoden zum Steuern der Animation während der Programmausführung.

1. reset () - setzt die Animation zurück und spielt sie zuerst ab.
   
2. setPause () - Unterbricht die Animation. Nimmt einen booleschen Wert als Parameter
   
3. setTimeOffset () - Legt den Zeitversatz vor dem Start der Animation fest.
   
4. setTimeMultiplier () - Legt den Zeitfaktor für die Beschleunigung / Verzögerung der Animation fest.
   

Um beispielsweise die Animation aus der Pause zu entfernen und zurückzusetzen, führen wir einen solchen Code aus

 apcb->setPause(false); apcb->reset(); 

und die Animation ab der vierten Sekunde nach dem Starten des Programms mit doppelter Beschleunigung zu starten, ein solcher Code

 apcb->setTimeOffset(4.0f); apcb->setTimeMultiplier(2.0f); 

6. Die Reihenfolge des Renderns von Grundelementen in OpenGL

OpenGL speichert Scheitelpunkt- und Grunddaten in verschiedenen Puffern, z. B. einem Farbpuffer, einem Tiefenpuffer, einem Schablonenpuffer usw. Außerdem überschreibt er nicht die Scheitelpunkte und Dreiecksflächen, die bereits an seine Pipeline gesendet wurden. Dies bedeutet, dass OpenGL eine neue Geometrie erstellt, unabhängig davon, wie die vorhandene Geometrie erstellt wurde. Dies bedeutet, dass die Reihenfolge, in der Grundelemente an die Rendering-Pipeline gesendet werden, das auf dem Bildschirm angezeigte Endergebnis erheblich beeinflusst.

Basierend auf den Tiefenpufferdaten zeichnet OpenGL undurchsichtige Objekte korrekt und sortiert die Pixel nach ihrem Abstand zum Beobachter. Bei Verwendung der Farbmischtechnik, beispielsweise beim Implementieren transparenter und durchscheinender Objekte, wird jedoch eine spezielle Operation ausgeführt, um den Farbpuffer zu aktualisieren. Die neuen und alten Pixel des Bildes werden unter Berücksichtigung des Werts des Alphakanals (vierte Farbkomponente) gemischt. Dies führt dazu, dass die Renderreihenfolge der durchscheinenden und undurchsichtigen Kanten das Endergebnis beeinflusst



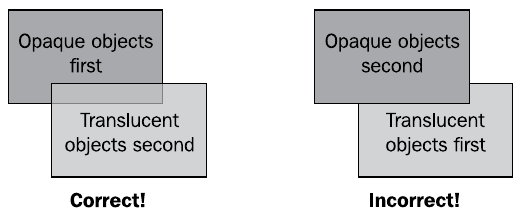
In der Abbildung wurden in der linken Situation zuerst undurchsichtige und dann transparente Objekte an die Pipeline gesendet, was zu einer korrekten Verschiebung des Farbpuffers und einer korrekten Anzeige der Gesichter führte. In der richtigen Situation wurden zuerst transparente Objekte und dann undurchsichtig gezeichnet, was zu einer falschen Anzeige führte.

Die Methode setRenderingHint () der Klasse osg :: StateSet gibt OSG die erforderliche Renderreihenfolge von Knoten und geometrischen Objekten an, falls dies explizit erfolgen muss. Diese Methode gibt lediglich an, ob durchscheinende Gesichter beim Rendern berücksichtigt werden sollen oder nicht. Dadurch wird sichergestellt, dass bei durchscheinenden Gesichtern in der Szene zuerst undurchsichtige und dann transparente Gesichter gezeichnet werden, wobei der Abstand zum Betrachter berücksichtigt wird. Um die Engine darüber zu informieren, dass dieser Knoten undurchsichtig ist, verwenden wir diesen Code

 node->getOrCreateStateSet()->setRenderingHint(osg::StateSet::OPAQUE_BIN); 

oder enthält transparente Kanten

 node->getOrCreateStateSet()->setRenderingHint(osg::StateSet::TRANSPARENT_BIN); 

7. Ein Beispiel für die Implementierung von durchscheinenden Objekten

Versuchen wir, die obige theoretische Einführung anhand eines konkreten Beispiels für die Implementierung eines durchscheinenden Objekts zu veranschaulichen.


Der hier gezeigte Code enthält größtenteils nichts Neues: Es werden zwei geometrische Objekte erstellt - ein strukturiertes Quadrat und ein Drachen, dessen Modell aus einer Datei geladen wird. Wir wenden jedoch eine weiße durchscheinende Farbe auf alle Eckpunkte des Quadrats an

 colors->push_back( osg::Vec4(1.0f, 1.0f, 1.0f, 0.5f) ); 

- Der Alpha-Kanal-Wert beträgt 0,5, was beim Mischen mit Texturfarben den Effekt eines durchscheinenden Objekts ergeben sollte. Zusätzlich sollte die Farbmischfunktion für die Transparenzverarbeitung eingestellt werden.

 osg::ref_ptr<osg::BlendFunc> blendFunc = new osg::BlendFunc; blendFunc->setFunction(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA); 

Übergabe an die OpenGL-Zustandsmaschine

 stateset->setAttributeAndModes(blendFunc); 

Beim Kompilieren und Ausführen dieses Programms erhalten wir das folgende Ergebnis



Hör auf! Und wo ist die Transparenz? Die Sache ist, dass wir vergessen haben, der Engine mitzuteilen, dass transparente Kanten verarbeitet werden sollen, was durch Aufrufen leicht gelöst werden kann

 stateset->setRenderingHint(osg::StateSet::TRANSPARENT_BIN); 

Danach erhalten wir das Ergebnis, das wir brauchen - der Drachenflügel leuchtet durch ein durchscheinendes strukturiertes Quadrat



Die Parameter der Mischfunktionen GL_SRC_ALPHA und GL_ONE_MINUS_SRC_ALPHA bedeuten, dass das resultierende Bildschirmpixel beim Zeichnen eines durchscheinenden Gesichts Farbkomponenten aufweist, die durch die Formel berechnet werden

 R = srcR * srcA + dstR * (1 - srcA) G = srcG * srcA + dstG * (1 - srcA) B = srcB * srcA + dstB * (1 - srcA) 

wobei [srcR, srcG, srcB] die Farbkomponenten der quadratischen Textur sind;[dstR, dstG, dstB] - Farbkomponenten jedes Pixels des Bereichs, auf dem eine durchscheinende Fläche überlagert ist, da der Hintergrund und die undurchsichtigen Kanten des Segelflugzeugflügels bereits an dieser Stelle gezeichnet sind. Mit srcA meine ich die Alpha-Komponente der Farbe des Quadrats.

Die Methode seRenderingHint () ordnet das Rendern von Grundelementen perfekt an, ist jedoch nicht sehr effizient, da das Sortieren transparenter Objekte nach Tiefe beim Rendern eines Frames eine ziemlich ressourcenintensive Operation ist. Daher sollte der Entwickler die Reihenfolge des Zeichnens der Gesichter selbst festlegen, wenn dies in den vorbereitenden Phasen der Szenenvorbereitung möglich ist.

8. Animation von Zustandsattributen

Mithilfe der Animation können Sie auch Statusattribute steuern. Durch Ändern der Eigenschaften eines oder mehrerer Rendering-Attribute können zahlreiche visuelle Effekte generiert werden. Diese Art von Animation, die den Status von Rendering-Attributen ändert, kann beim Aktualisieren der Szene einfach über den Rückrufmechanismus implementiert werden.

Klassen von Standardinterpolationen können auch verwendet werden, um die Funktion zum Ändern von Attributparametern anzugeben.

Wir haben bereits Erfahrung in der Erstellung von durchscheinenden Objekten. Wir wissen, dass wir, wenn die Alpha-Komponente der Farbe Null ist, ein vollständig transparentes Objekt mit einem Wert von 1 erhalten - vollständig undurchsichtig. Es ist klar, dass durch zeitliches Variieren dieses Parameters von 0 bis 1 der Effekt des allmählichen Auftretens oder Verschwindens eines Objekts erhalten werden kann. Wir veranschaulichen dies anhand eines konkreten Beispiels.


Wir beginnen mit der Erstellung eines Callback-Handlers zum Ändern des Werts des Alphakanals im Laufe der Zeit

 class AlphaFadingCallback : public osg::StateAttributeCallback { public: AlphaFadingCallback() { _motion = new osgAnimation::InOutCubicMotion(0.0f, 1.0f); } virtual void operator() (osg::StateAttribute* , osg::NodeVisitor*); protected: osg::ref_ptr<osgAnimation::InOutCubicMotion> _motion; }; 

Der geschützte Parameter _motion bestimmt die Funktion, mit der sich der Alpha-Wert im Laufe der Zeit ändert. In diesem Beispiel wählen wir die kubische Spline-Näherung und setzen sie sofort im Klassenkonstruktor

 AlphaFadingCallback() { _motion = new osgAnimation::InOutCubicMotion(0.0f, 1.0f); } 

Diese Abhängigkeit kann durch eine solche Kurve veranschaulicht werden.



Im Konstruktor des InOutCubicMotion-Objekts bestimmen wir die Grenzen des approximierten Werts von 0 bis 1. Als nächstes definieren wir den Operator () für diese Klasse auf diese Weise neu

 void AlphaFadingCallback::operator()(osg::StateAttribute *sa, osg::NodeVisitor *nv) { (void) nv; osg::Material *material = static_cast<osg::Material *>(sa); if (material) { _motion->update(0.0005f); float alpha = _motion->getValue(); material->setDiffuse(osg::Material::FRONT_AND_BACK, osg::Vec4(0.0f, 1.0f, 1.0f, alpha)); } } 

Holen Sie sich einen Zeiger auf das Material

 osg::Material *material = static_cast<osg::Material *>(sa); 

Der abstrakte Wert des Attributs wird zurückgerufen. Wir werden diesen Handler jedoch an das Material anhängen. Daher ist es der Zeiger auf das kommende Material. Daher können wir das Statusattribut sicher in den Zeiger auf das Material konvertieren. Als nächstes legen wir das Aktualisierungsintervall der Approximationsfunktion fest - je größer es ist, desto schneller ändert sich der Parameter innerhalb des angegebenen Bereichs

 _motion->update(0.0005f); 

Wir lesen den Wert der Approximationsfunktion

 float alpha = _motion->getValue(); 

und geben Sie dem Material einen neuen diffusen Farbwert

 material->setDiffuse(osg::Material::FRONT_AND_BACK, osg::Vec4(0.0f, 1.0f, 1.0f, alpha)); 

Lassen Sie uns nun die Szene in der Funktion main () bilden. Ich denke, Sie sind jedes Mal müde, ein Quadrat auf den Eckpunkten zu erstellen. Deshalb vereinfachen wir die Aufgabe - wir generieren ein quadratisches Polygon mit der Standard-OSG-Funktion

 osg::ref_ptr<osg::Drawable> quad = osg::createTexturedQuadGeometry( osg::Vec3(-0.5f, 0.0f, -0.5f), osg::Vec3(1.0f, 0.0f, 0.0f), osg::Vec3(0.0f, 0.0f, 1.0f)); 

Der erste Parameter ist der Punkt, von dem aus die untere linke Ecke des Quadrats erstellt wird. Die beiden anderen Parameter geben die Koordinaten der Diagonalen an. Nachdem wir das Quadrat herausgefunden haben, erstellen wir Material dafür

 osg::ref_ptr<osg::Material> material = new osg::Material; material->setAmbient(osg::Material::FRONT_AND_BACK, osg::Vec4(0.0f, 0.0f, 0.0f, 1.0f)); material->setDiffuse(osg::Material::FRONT_AND_BACK, osg::Vec4(0.0f, 1.0f, 1.0f, 0.5f)); 

Wir geben die Farboptionen des Materials an. Umgebungsfarbe ist ein Parameter, der die Farbe des Materials im schattierten Bereich kennzeichnet, auf den Farbquellen keinen Zugriff haben. Diffuse Farbe ist die Farbe des Materials, die die Fähigkeit einer Oberfläche charakterisiert, die darauf fallende Farbe zu diffundieren, das heißt, was wir im Alltag als Farbe bezeichnen. Der Parameter FRONT_AND_BACK gibt an, dass dieses Farbattribut sowohl der Vorder- als auch der Rückseite der Geometrieflächen zugewiesen ist.

Weisen Sie dem zuvor erstellten Handler Material zu.

 material->setUpdateCallback(new AlphaFadingCallback); 

Ordnen Sie das erstellte Material dem Quadrat zu

 geode->getOrCreateStateSet()->setAttributeAndModes(material.get()); 

und andere Attribute festlegen - die Funktion zum Mischen von Farben und zum Anzeigen, dass dieses Objekt transparente Kanten hat

 geode->getOrCreateStateSet()->setAttributeAndModes(new osg::BlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)); geode->getOrCreateStateSet()->setRenderingHint(osg::StateSet::TRANSPARENT_BIN); 

Wir vervollständigen die Bildung der Szene und führen den Betrachter aus

 osg::ref_ptr<osg::Group> root = new osg::Group; root->addChild(geode.get()); root->addChild(osgDB::readNodeFile("../data/glider.osg")); osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); 

Wir erhalten das Ergebnis in Form eines Quadrats, das reibungslos in der Szene erscheint

Anstelle einer Schlussfolgerung: eine kleine Bemerkung zu Abhängigkeiten

Sicherlich wird Ihr Beispiel nicht kompiliert, was zu einem Fehler in der Erstellungsphase führt. Dies ist kein Zufall - achten Sie auf die Zeile in der Header-Datei main.h

 #include <osgAnimation/EaseMotion> 

Das OSG-Header-Verzeichnis, aus dem die Header-Datei entnommen wird, verweist normalerweise auf die Bibliothek, die die Implementierung der im Header beschriebenen Funktionen und Klassen enthält. Daher sollte das Erscheinungsbild des Verzeichnisses osgAnimation / darauf hindeuten, dass eine gleichnamige Bibliothek zur Linkliste des Projekterstellungsskripts hinzugefügt wird (unter Berücksichtigung der Pfade zu Bibliotheken und der Erstellungsversion).

 LIBS += -losgAnimation 

Fortsetzung folgt...