Geschichte der Shipastik

Spikes überall

Wir nennen ihn Spikey und in meinem heutigen Leben treffe ich ihn ständig:



Es stammt von einem dreidimensionalen Objekt, einem Polyeder namens "Rhombic Sixtieth".



Aber was ist ihre Geschichte und warum haben wir sie zu unserem Symbol gemacht?

Der Ursprung des Dorns

Als wir 1987 die erste Version von Mathematica entwickelten, war eine ihrer Innovationen die Möglichkeit, auflösungsunabhängige dreidimensionale Grafiken auf der Grundlage symbolischer Beschreibungen zu erstellen. In frühen Demonstrationen konnten wir überraschend klare Bilder von regulären Polyedern erzeugen. Kurz vor der Veröffentlichung von Mathematica 1.0 wollten wir jedoch ein eindrucksvolleres Beispiel verwenden. Aus diesem Grund haben wir uns entschlossen, das letzte reguläre Polyeder - das Ikosaeder - zu nehmen und daraus etwas Komplexeres zu machen, indem wir ihm eine Sternform oder genauer gesagt eine Kumulierung geben. Ja, so sah die erste Notebook-Oberfläche vor 30 Jahren aus.



Anfangs war es nur eine nette Demonstration, die auf unseren damaligen Computern ziemlich schnell funktionierte. Bald jedoch wurde das von ihm erzeugte dreidimensionale Objekt de facto als Logo für Mathematica verwendet. Und als 1988 die Version 1.0 veröffentlicht wurde, war das sternförmige Ikosaeder überall:



Im Laufe der Zeit tauchten verschiedene Widmungen für unser Sternpolyeder auf - hergestellt in verschiedenen Materialien und Größen:



Aber nur ein Jahr nach der Veröffentlichung von Mathematica 1.0 waren wir bereit, Mathematica 1.2 zu veröffentlichen, und um die Komplexität des Produkts zu vermitteln, brauchten wir ein ausgeklügeltes Logo. Einer unserer Entwickler, Igor Rivin, verteidigte seine Doktorarbeit über Polyeder im hyperbolischen Raum - und dank seiner Bemühungen wurden Materialien für Version 1.2 mit einem hyperbolischen Ikosaeder verziert:



Meine Mitarbeiter gaben mir 1989 zu meinem 30. Geburtstag ein T-Shirt mit der damals modernen Shipastik und ein Zitat, das ich auch nach so vielen Jahren unterstütze:


"Gesellschaft macht Spaß"

Nach der Veröffentlichung von Mathematica 1.2 konnte man in unseren Marketingmaterialien eine ganze Sammlung hyperbolischer regulärer Polyeder finden, aber mit dem Aufkommen von Version 2.0 im Jahr 1991 entschieden wir, dass uns das hyperbolische Ikosaeder am besten gefiel:



Aber wir haben weiter andere Formen mit Stacheln erforscht. Inspiriert von Leonardo da Vincis Zeichnung eines „Holzmodells“ des sternförmigen Ikosaeders (mit überraschend genauer Perspektive) für Luke Paciolis Buch „On Divine Proportion“ bestellten wir ein Poster der Version 2.0, auf dem fünf sich kreuzende Tetraeder so angeordnet sind, dass ihre äußeren Eckpunkte das Dodekaeder bilden:



Wenn ich heute in meinen Archiven von 1991 nachschaue, finde ich den „erklärenden“ Code, und es ist schön zu sehen, dass er in unserer neuesten Version von Wolfram Language leicht ausgeführt werden kann (obwohl er heute etwas eleganter geschrieben werden kann):



Im Laufe der Jahre ist dies zu einem seltsamen Ritual geworden. In Vorbereitung auf den Start der nächsten Hauptversion von Mathematica werden wir ernsthafte Treffen organisieren, bei denen wir uns mit der „Auswahl eines neuen Shipastik“ beschäftigen. Manchmal müssen Sie aus Hunderten verschiedener Optionen auswählen, die mit völlig unterschiedlichen Algorithmen erstellt wurden:



Obwohl Farbpaletten mutieren und Shipastiks häufig das Vorhandensein neuer Funktionen im System widerspiegeln (wenn auch etwas implizit), haben wir eine 30-jährige Tradition bei der Auswahl von Optionen für ein hyperbolisches Dodekaeder:



In letzter Zeit ist es üblich geworden, den parametrischen Raum zu untersuchen - obwohl wir jetzt bereits Hunderte von Parametern akkumuliert haben:



Das hyperbolische Dodekaeder hat 20 Spitzen - es war ideal, um das 20-jährige Jubiläum von Mathematica im Jahr 2008 zu feiern. Als wir 2013 zum 25-jährigen Jubiläum etwas Ähnliches machen wollten, standen wir vor dem Problem, dass es keine regulären Polyeder mit 25 Eckpunkten gibt. Wir konnten jedoch (mithilfe der SpherePoints- Funktion [25]) eine ungefähre Zahl erstellen und diese für alle Mitarbeiter des Unternehmens auf einem 3D-Drucker drucken, wobei die Größe der Dienstzeit der Mitarbeiter entspricht.

Beenden Sie Wolfram | Alpha

2009 bereiteten wir uns auf die Veröffentlichung von Wolfram | Alpha vor und das System benötigte ein Logo. Es gab viele Konzepte:



Wir wollten betonen, dass Wolfram | Alpha durch Berechnungen funktioniert und nicht etwa als Suchmaschine. Und für einige Zeit wollten wir etwas mit Zahnrädern verwenden. Wir wollten aber auch, dass das Logo dem langjährigen Mathematica-Logo ähnelt. Dies führte zu einem dieser Projekte wie "Unser General wurde verrückt": der Schaffung eines Getriebes aus Stachelformen.

Sandor Kabai, ein langjähriger Benutzer von Mathematica und Wolfram Language, ein Maschinenbauingenieur aus Ungarn, half uns mit dem Vorschlag von „Stachelgetrieben“:



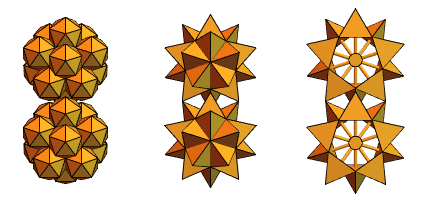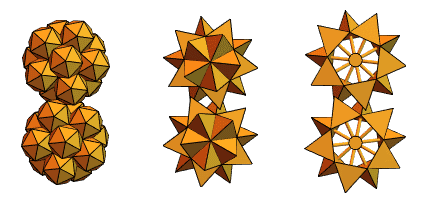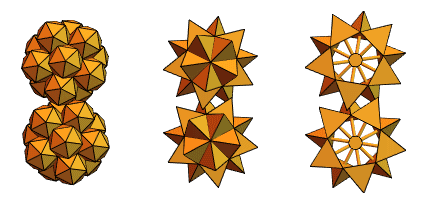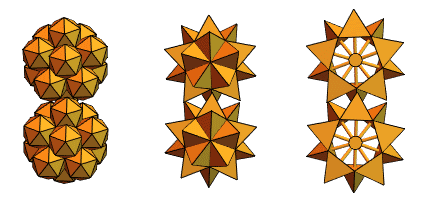
Zurück zu den sich kreuzenden Tetraedern aus Version 2, schuf er so etwas:



Im Jahr 2009 wurden 3D-Drucker sehr beliebt, und wir dachten, es wäre schön, ein Logo für Wolfram | Alpha zu erstellen, das gedruckt werden könnte. Das hyperbolische Polyeder passte nicht - die Stacheln konnten abbrechen und eine Bedrohung darstellen. Formen wie Spikes der 4. Version mit "sicheren Spikes" mangelte es an Eleganz.

Für eine Weile klammerten wir uns an eine Idee mit Zahnrädern. Aber am Ende entschieden sie, dass es sich lohnt, sich gewöhnliche Polyeder noch einmal anzusehen. Aber welches Polyeder können wir wählen?

Natürlich gibt es unendlich viele mögliche Polyeder. Für unser Logo wollten wir jedoch ein symmetrisches und zum Teil „richtiges“ Polyeder wählen. Fünf reguläre Polyeder (oder „platonische Körper“), deren Flächen dieselben regulären Polygone sind, können als die „regelmäßigsten“ von allen angesehen werden:



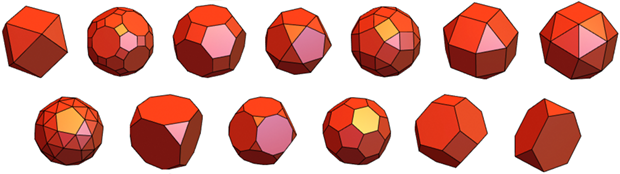
Es gibt 13 weitere archimedische Körper - sie haben identische Eckpunkte, und regelmäßige Polygone, obwohl unterschiedlicher Art, wirken als Gesichter:



Es gibt viele Arten von „Korrektheit“ von Polyedern. Ein Beispiel sind die „homogenen Polyeder“, die ein Poster aus dem Mathematica Journal von 1993 zeigt:



Im Laufe der Jahre, in denen Eric Weinstein die Sammlung sammelte, die 1999 zu MathWorld geworden war, versuchte er, Artikel über so viele Polygone wie möglich aufzunehmen. Im Jahr 2006 haben wir im Rahmen der Aufnahme verschiedener systematisierter Daten in Mathematica und Wolfram Language begonnen, Polygondaten in MathWorld aufzunehmen. Als Ergebnis erschien nach der Veröffentlichung von Version 6.0 im Jahr 2007 die PolyhedronData- Funktion, die umfassende Daten zu 187 bemerkenswerten Polygonen enthielt:



In Mathematica und Wolfram Language konnten Sie immer reguläre Polygone generieren, aber jetzt ist dies einfacher geworden. Mit Version 6.0 haben wir auch das Wolfram Demonstrations Project veröffentlicht, das sich schnell mit verschiedenen Demos zu Polyedern füllte.

Eine davon wurde von meiner Tochter Katerina im Alter von 10 Jahren hergestellt (heute entwickelt sie sich auf dem Gebiet der Geometrie weiter): Dies sind „polyedrische Koalas“, die von allen verwendeten Polyedern aus PolyhedronData [] aufgeschlüsselt werden:



Vor diesem Hintergrund wollten wir 2009 für Wolfram | Alpha „ein Polyeder wählen“. Alles wurde am Freitag, dem 6. Februar, entschieden, als ich mich an die Arbeit machte.

Ich habe dieses Notizbuch aufbewahrt und es zeigt, dass ich zuerst versucht habe, die zweifelhafte Idee umzusetzen, Kugeln an den Eckpunkten von Polyedern zu platzieren:



Aber wie in der Notebook-Geschichte aufgezeichnet, wechselte ich nur zwei Minuten später zu reinen Polyedern - sie waren alle orange, die wir dann für das Logo verwenden wollten:





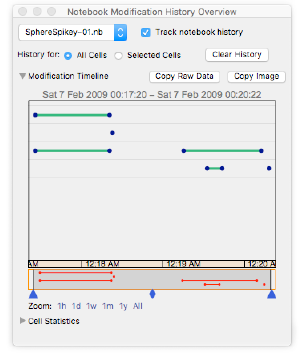
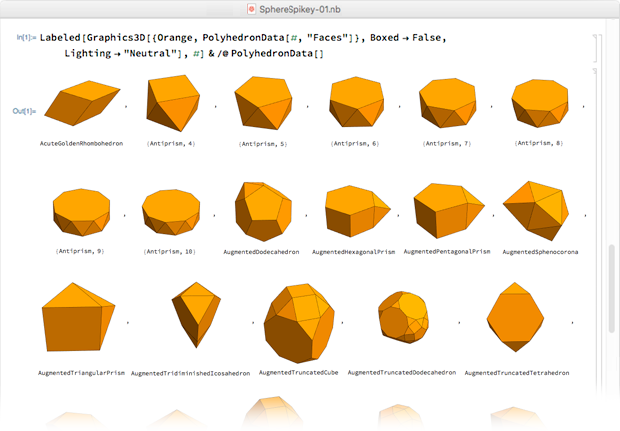
Die Polyeder waren in alphabetischer Reihenfolge nach Namen angeordnet, und in der 28. Zeile erschien er - ein rhombisches Hexaeder.



Ein paar Minuten später, am 7. Februar 2009, um 00:24:24 Uhr, entdeckte ich dieses rhombische Hexaeder und verwandelte es in eine symmetrische Position, die wir jetzt verwenden:



Ich wollte sehen, wie es in Grau und Silhouette aussehen würde, und vier Minuten später benutzte ich ColorSeparate , um herauszufinden:



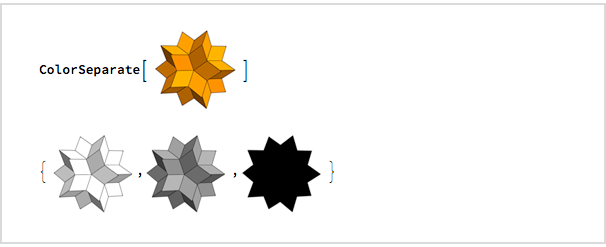
Ich fing sofort an, eine E-Mail zu schreiben, die ich um 00:32 Uhr schickte:

Ich mag RhombicHexecontahedron wirklich. Es hat eine interessante und sehr symmetrische Form. Es scheint mir, dass seine Genauigkeit genau zu uns passt und die Silhouette ziemlich vernünftig aussieht.



Offensichtlich habe ich gerade RhombicHexecontahedron aus dem Notizbuch kopiert (ich bezweifle, dass ich das Sechseck [Hexecontahedron] ohne Fehler hätte schreiben können). Aus meinen Archiven weiß ich, dass ich zum ersten Mal den Namen des Polyeders geschrieben habe, das dazu bestimmt ist, mein Favorit zu werden.

In Wolfram Language war es sehr einfach, sich ein Bild von einem rhombischen Hexaeder zu machen und damit zu spielen:



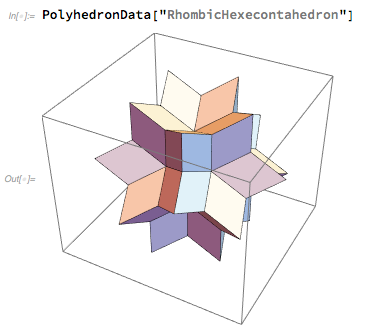
Am Montag war klar, dass das rhombische Hexaeder gewonnen hatte - und unsere visuelle Abteilung war damit beschäftigt, es als Logo für Wolfram | Alpha zu erstellen. Wir haben verschiedene Ausrichtungen ausprobiert, aber am Ende haben wir uns für die von mir gewählte symmetrische Position „in voller Sicht“ entschieden. (Wir mussten auch die beste „Brennweite“ für den am besten geeigneten Winkel auswählen).



Wie unser stelliertes Ikosaeder aus Version 1.0 hat das rhombische Hexaeder 60 Gesichter. Aber irgendwie sieht es dank der „Fünf-Blütenblätter“ -Kombinationen viel eleganter aus. Es wurde sehr viel Aufwand betrieben, um eine solche Schattierung der Gesichter so zu wählen, dass die zweidimensionale Zeichnung das dreidimensionale Objekt korrekt widerspiegelte. Aber bald haben wir die erste offizielle Version unseres Logos eingeführt:



Sie tauchte schnell überall auf und als Hommage an unsere frühen Ideen oft vor einem mit Zahnrädern geschmückten Hintergrund:



Einige Jahre später haben wir die Schattierung der Kanten leicht korrigiert, was zur Schaffung des Wolfram | Alpha-Logos führte, das immer noch verwendet wird:



Rhombisches Sechseck

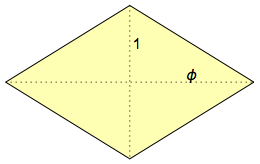
Was ist ein rhombisches Hexaeder? Im Englischen heißt es Hexekontaeder, weil es 60 Gesichter hat, und ἑξηκοντα (hexekont) ist das griechische Wort für „60“. Seine Gesichter sind goldene Rauten , die so benannt sind, weil ihre Diagonalen gemäß dem goldenen Schnitt miteinander in Beziehung stehen: φ = (1 + √5) / 2 & sime; 1,618:



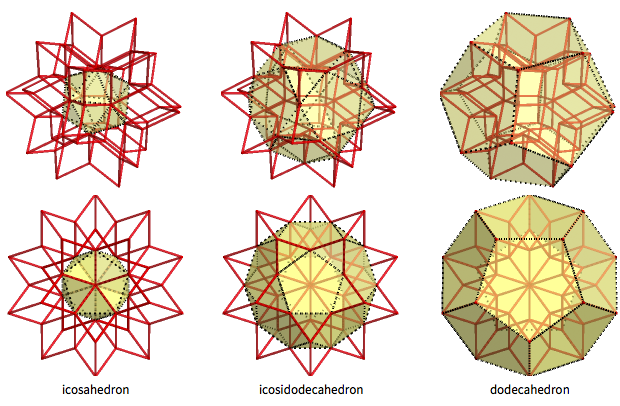
Das rhombische Hexaeder ist ein interessanter Zwischenkörper zwischen dem Ikosaeder und dem Dodekaeder (mit dem Ikosaderkaeder dazwischen). Die 12 inneren Eckpunkte des rhombischen Hexaeders bilden das reguläre Ikosaeder, und die 20 äußeren Eckpunkte bilden das reguläre Dodekaeder. 30 „Zwischenpeaks“ bilden das 32-facettierte Ikosododekaeder (es hat 20 dreieckige und 12 fünfeckige Flächen):



Insgesamt hat das rhombische Hexaeder 62 Eckpunkte und 120 Kanten (sowie 120-62 + 2 = 60 Flächen). Es gibt drei Arten von Eckpunkten ("intern", "mittel" und "extern"), die 12 + 30 + 20 Eckpunkten des Ikosaeders, des Ikosododekaeders und des Dodekaeders entsprechen. An diesen Eckpunkten laufen die Kanten 3, 4 und 5 zusammen. Jede Fläche hat einen „internen“ Scheitelpunkt, an dem sich 5 Kanten treffen, einen externen Scheitelpunkt, an dem sich drei Kanten treffen, und zwei „Zwischenpunkte“, an denen sich 4 Kanten treffen. Die äußeren und inneren Eckpunkte sind die spitzwinkligen Eckpunkte der goldenen Rauten, und die mittleren sind stumpfwinklig.

Der Winkel an den spitzen Spitzen der goldenen Rauten beträgt 2 tan ^–1 (φ ^–1 ) ≤ 63,43 ° und an den stumpfen Spitzen 2 tan ^–1 (φ) ≤ 116,57 °. Mit solchen Winkeln können Sie ein rhombisches Hexaeder aus dem Zometool- Konstruktor nur mit den roten Trägern zusammensetzen (wie im Fall des Dodekaeders):



Von 120 Kanten des rhombischen Hexaeders mit 60 „inneren Scharnieren“ beträgt der Diederwinkel 4π / 5 = 144 ° und für 60 äußere 2π / 5 = 72 °. Die Winkel, die durch die äußeren und inneren Eckpunkte zusammengezogen werden, sind π / 5 und 3π / 5.

Um ein rhombisches Hexaeder zu zeichnen, müssen Sie die dreidimensionalen Koordinaten seiner Eckpunkte kennen. Sie werden bequem durch die Tatsache erhalten, dass das rhombische Hexaeder in Bezug auf die Ikosaedergruppe unveränderlich ist. Sie können also mit einer goldenen Raute beginnen und einfach 60 Matrizen hinzufügen, die eine dreidimensionale Darstellung der Ikosaedergruppe bilden. Dies gibt zum Beispiel die Endkoordinaten der Eckpunkte in {± φ, ± 1,0}, {± 1, ± φ, ± (1 + φ)}, {± 2φ, 0,0}, {± φ, ± ( 1 + 2φ), 0}, {± (1 + φ), ± (1 + φ), ± (1 + φ)} und ihre zyklischen Permutationen mit allen möglichen Vorzeichen.

Zusätzlich zu der Tatsache, dass die Flächen eines rhombischen Hexaeders goldene Rauten sind, kann ein rhombisches Hexaeder aus 20 goldenen Rhomboedern konstruiert werden (wobei alle sechs Flächen goldene Rauten sind):



Es gibt andere Möglichkeiten, aus anderen Polyedern ein rhombisches Hexaeder zu erzeugen. Es kann aus fünf sich kreuzenden Würfeln und aus 182 Dodekaedern in Kontakt mit Gesichtern erhalten werden:



Sie können kein durchgehendes Mosaik aus rhombischen Sechzig-Hexaedern auslegen, aber sie passen gut zusammen (und ja, ich habe Dutzende von Shipastiks aus Papier gesehen, die sich auf diese Weise falten):



Sie können daraus auch alle Arten von Ringen und andere Konfigurationen erstellen:



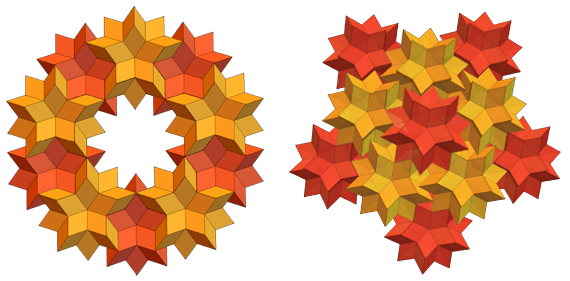
Ein enger Verwandter des rhombischen Hexaeders (RS) ist das rhombische 30-Tetraeder (RT). RS und RT haben Gesichter, die goldene Rauten sind. Aber RS ​​hat 60 davon und RT hat 30. So sieht eine separate RT aus:



Mehrere RTs sind perfekt in RS-Taschen investiert, und ähnliche Dinge stellen sich heraus:



Sandor Kabay, der bereits erwähnt wurde, interessierte sich um 2002 für RSh und RT. Und nach dem Start des Wolfram-Demonstrationsprojekts fügte er zusammen mit dem slowenischen Mathematiker Isidor Hafner dem Projekt mehr als hundert Demonstrationen hinzu, die sich auf RS, RT und viele ihrer Eigenschaften beziehen:

Stachelige Papiermodelle

Sobald wir uns für Shipastik als RS entschieden hatten, begannen wir mit der Erstellung seiner 3D-Modelle. Jetzt ist es sehr einfach, dies mit der Funktion Printout3D [PolyhedronData [...]] zu tun, und bereits berechnete Modelle können auf Ressourcen von Drittanbietern gefunden werden .

Im Mai 2009, als Wolfram | Alpha gestartet wurde, hatten wir bereits viele 3D-Spikes zur Hand:



Als wir uns auf die erste Weihnachtszeit nach dieser Veranstaltung vorbereiteten, beschlossen wir, jedem die Möglichkeit zu geben, seine eigene dreidimensionale Shipastik herzustellen. Zunächst haben wir die Option mit 20 rhomboedrischen Magneten in Betracht gezogen, die mit Kunststoff beschichtet sind. Aber sie kamen teuer heraus und hielten nicht sehr gut zusammen.

Dies führte uns zu der Idee, Shipastik aus Papier oder dünnem Karton herzustellen. Deshalb wollten wir zunächst ein Schema erstellen, das in Shipastika gefaltet werden kann:



Meine Tochter Katerina diente als Testerin (und sie hat immer noch eine Testprobe), aber es wurde klar, dass beim Falten viele unangenehme Situationen auftreten, in denen unklar ist, wie man sich von einer Position zur anderen bewegt. Sie können eine große Anzahl von Layouts erstellen (es gibt 43.380 davon nur für das Dodekaeder und das Ikosaeder) - und wir dachten, dass es vielleicht möglich wäre, etwas Besseres aus ihnen auszuwählen:



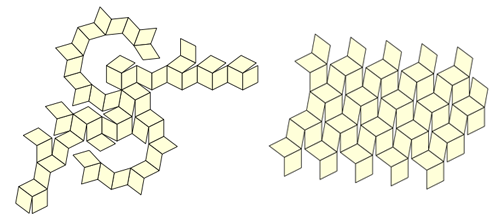
Aber als wir ein solches Schema nicht finden konnten, hatten wir eine neue (wenn auch offensichtliche) Idee: Wenn das Modell an den Ohren festhalten würde, warum nicht aus ein paar Teilen machen? Wir haben schnell erkannt, dass Sie dafür nur 12 identische Stücke dieser Art nehmen müssen:



Mit ihrer Hilfe haben wir unsere " Sets für Papierskulpturen " erstellt:



Eine interessante Aufgabe bestand darin, leicht verständliche Anweisungen zu schreiben, aber nach mehreren Iterationen wurden die Anweisungen gut entwickelt und einfach:



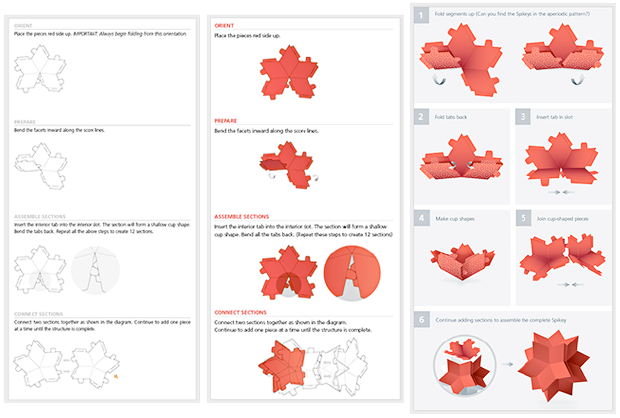
Und nachdem die Zeitung Shipastiks zu den Menschen gegangen war, begannen unsere Benutzer, uns alle Arten von Shipastik-Bildern „vor Ort“ zu senden:

Der Weg zum rhombischen Sechseck

Der vielseitige Würfel aus dem alten Ägypten

Es ist nicht bekannt, wer zuerst die platonischen Körper beschrieben hat. Vielleicht wurde dies von den Pythagoräern getan (die in der Nähe so großer Ablagerungen von facettenreichen Pyritkristallen lebten). Vielleicht hat das jemand lange vor ihnen getan. Vielleicht war es ein Zeitgenosse von Platon, Teetet von Athen . Jedenfalls waren zur Zeit Platons (ca. 400 v. Chr.) Fünf platonische Körper bekannt. Und als Euklid seine Elemente schrieb (ca. 300 g v. Chr.), War eine der Säulen dieser Arbeit der Beweis für das Fehlen anderer regulärer Polyeder. Dieser Beweis ist dafür bekannt, dass er die meisten Schritte von den ursprünglichen euklidischen Axiomen unternimmt - 32.

Platonische Feststoffe wurden für Würfel und Ornamente verwendet. Ihm wurde aber auch eine zentrale Rolle beim Denken über die Natur zugewiesen - zum Beispiel schlug Platon vor, dass in gewissem Sinne alles aus ihnen bestehen könnte: Erde aus Würfeln, Luft aus Oktaedern, Wasser aus Ikosaedern, Feuer aus Tetraedern und Himmel („Äther“). ) aus Dodekaedern.

Was ist mit anderen Polyedern? Im 4. Jahrhundert v. Papp von Alexandria schrieb, dass einige Jahrhunderte bevor Archimedes 13 andere "reguläre Polyeder" entdeckte - anscheinend sogenannte archimedische Körper - obwohl die Details davon verloren gehen. Und seit tausend Jahren ist Polyedern wenig passiert. Aber im 15. Jahrhundert, mit dem Beginn der Renaissance, wurden Polyeder plötzlich wieder in Mode. Leonardo da Vinci und Albrecht Dürer verwendeten sie regelmäßig in Kunst und Design, um einige der archimedischen Körper wiederzuentdecken - und um neue Polyeder zu entdecken, zum Beispiel das Ikodosodekaeder.

Der größte Fortschritt für die Polyeder war jedoch das Werk von Johannes Kepler zu Beginn des 17. Jahrhunderts. Alles begann mit einer eleganten, wenn auch völlig falschen Theorie. Kepler glaubte auf der Grundlage theologischer Annahmen, dass das Universum mit mathematischer Präzision erschaffen werden sollte, und schlug vor, dass sich die sechs damals bekannten Planeten entlang verschachtelter Kugeln bewegen, die um fünf platonische Körper herum eingeschrieben und beschrieben sind:



In seinem 1619 erschienenen Buch Harmonices mundi, Harmony of the World, argumentierte Kepler, dass viele Merkmale von Musik, Planeten und Seelen nach ähnlichen geometrischen Beziehungen und Prinzipien arbeiten. Um die Argumente zu bestätigen, untersuchte Kepler Polygone und Polyeder und interessierte sich insbesondere für Objekte, die vollständige Mengen bilden, wie platonische Körper.

Er studierte die "Kontaktpolyeder", mit denen das Flugzeug gepflastert werden sollte - und fand zum Beispiel " monströse Kacheln ", wie er sie nannte (bestehend aus Pentagonen, Pentagrammen und Dekagonen). Er studierte die „Sternpolyeder“ und fand verschiedene Sternversionen platonischer Körper (und des Kepler-Poinsot-Körpers ). 1611 veröffentlichte er ein kleines Buch über die sechseckige Struktur von Schneeflocken, das einem seiner Gönner als Geschenk für das neue Jahr geschrieben wurde. In diesem Buch diskutierte er die dreidimensionale Packung von Kugeln (und sphärischen Atomen) und schlug eine Hypothese vor, dass die dichteste Packung von Kugeln im dreidimensionalen Raum (wir beobachten regelmäßig ihre Implementierung in Obstpackungen in Geschäften) eine flächenzentrierte kubische Packung ist (diese Hypothese wurde erst nach 2000 formal bewiesen Jahre - mit Mathematica).

In verschiedenen Kepler-Paketen sind verschiedene Polyeder versteckt. Beginnen wir mit einer beliebigen Kugel, nehmen wir ihre Nachbarn und verbinden ihre Zentren, um die Eckpunkte des Polyeders zu bilden. In Keplers engster Packung berühren 12 andere eine Kugel, und aus ihren Zentren wird ein Kuboktaeder mit 12 Eckpunkten und 14 Flächen erhalten. Kepler beschrieb aber auch ein anderes Paket, 8% weniger dicht, in dem jede Kugel von 8 anderen bedeckt ist und weitere 6 sehr nahe beieinander liegen. Wenn wir ihre Zentren verbinden, erhalten wir ein rhombisches Dodekaeder mit 14 Eckpunkten und 12 Flächen:



Nachdem Kepler dies entdeckt hatte, begann er nach anderen „rhombischen Polyedern“ zu suchen. In dem von ihm gefundenen rhombischen Dodekaeder bestanden die Rauten aus Paaren gleichseitiger Dreiecke. 1619 studierte Kepler aber auch goldene Rauten - und fand eine rhombische Dreißig-Seiten-Raute, nach der er in seinem Buch sein schönes Bild neben dem rhombischen Dodekaeder malte:



Kepler fand sofort Anwendung für rhombische Polygone: Er wollte sie und einen Würfel verwenden, um ein Modell verschachtelter Kugeln zu erstellen, das für die Umlaufbahnen der vier Jupitermonde geeignet ist, die 1610 von Galileo entdeckt wurden.

Warum hat Kepler das rhombische Hexaeder nicht geöffnet? Ich denke, er kam ihm ziemlich nahe. Er studierte nicht konvexe Sternpolyeder. Er sah rhombische Polyeder an. Aber anscheinend genügte für seine astronomischen Theorien eine rhombische Dreißigseitigkeit, wonach er aufhörte zu suchen.

Infolgedessen wurden Keplers Gesetze, die nicht mit dem Polyeder zu tun hatten, natürlich zum Hauptbeitrag zur Astronomie, die es überlebte. Keplers Arbeit am Polyeder - wenn auch im Rahmen einer falschen physikalischen Theorie - bleibt jedoch ein ewiger Beitrag zur Mathematik.

In den nächsten drei Jahrhunderten wurden mehr Polyeder unterschiedlicher Korrektheit gefunden - und zu Beginn des 20. Jahrhunderts kannten Mathematiker bereits viele ihrer Typen:



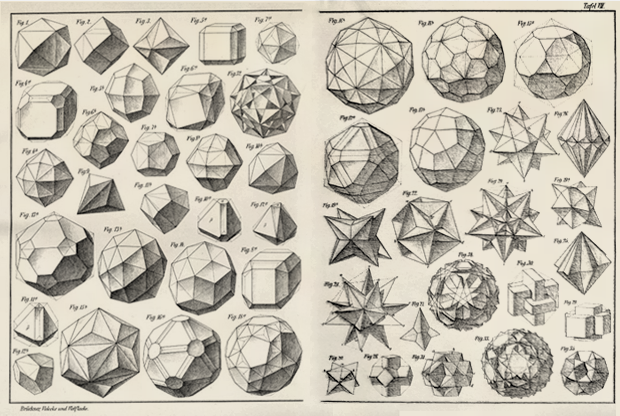
Aber soweit ich das beurteilen kann, gab es keine RS unter ihnen. Seine Entdeckung erwartete die Arbeit von Helmut Unkelbach . 1910 geboren, verteidigte er 1937 seine Promotion in Mathematik an der Universität München (obwohl er zuerst Physik studierte). Er schrieb mehrere Arbeiten zur konformen Kartierung und veröffentlichte 1940 - möglicherweise aufgrund der Untersuchung der Kartierung von Polyedern - die Arbeit "Edge-Symmetric Polyhedra" in deutscher Sprache.

Er erklärte, sein Ziel sei eine umfassende Untersuchung aller möglichen Polyeder, die eine spezielle neue Definition der Korrektheit erfüllen: Alle Kanten haben die gleiche Länge und liegen in der Symmetrieebene des Polyeders. Das Hauptergebnis der Arbeit war eine Tabelle mit 20 verschiedenen Polyedern dieser Eigenschaft:


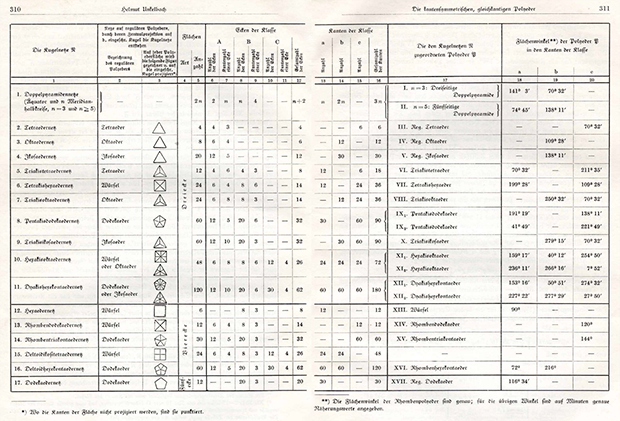Klickbar

Die meisten von ihnen waren bereits berühmt. Aber Unkelbach wählte drei davon aus, die er für neu hielt: zwei Hexaciscosahedra (oder Disdakis-Dodekaeder), zwei Hexacisicosahedra (oder Disdacystriacontahedron) und das, was er Rhombenhexekontaeder nannte, oder ein rhombisches Hexaeder. Und er betrachtete RSh eindeutig als seine Hauptleistung und legte ein Foto seines Modells bei, das er selbst angefertigt hatte:



Wie hat er RS ​​gebracht? Er begann mit dem Dodekaeder und definierte zwei seiner Symmetrieebenen:



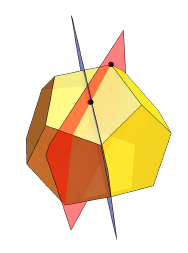
Dann teilte jedes seiner Gesichter:



Dann drückte er im Wesentlichen die Zentren jedes der Gesichter um einen Abstand heraus, der dem üblichen Abstand zum Zentrum multipliziert mit einem bestimmten α entspricht:



Für α <1 kreuzten sich die resultierenden Flächen nicht. Bei den meisten Werten von α waren ihre Seiten jedoch nicht gleich. Dies geschieht nur in einem bestimmten Fall - wenn das resultierende Polyeder genau mit dem RS übereinstimmt.

Unkelbach betrachtete seine Arbeit von 1940 als „Aufwärmübung“ für eine umfassendere Untersuchung von „k-symmetrischen Polyedern“ mit weniger strengen Symmetrieanforderungen. Aber schon jetzt war es ein Wunder, dass nach Beginn des Zweiten Weltkriegs in Deutschland eine mathematische Zeitschrift veröffentlicht wurde - kurz nach dieser Veröffentlichung wurde Unkelbach an die Front gerufen, wo er mehrere Jahre lang akustische Torpedos für die deutsche Flotte entwickelte.

Er veröffentlichte keine weiteren Werke über Polyeder und starb 1968. Nach Jahren kehrte er zur konformen Kartierung zurück und begann auch, über die Theorie der Abstimmung zu publizieren, wobei er sie als Schlüssel zur Schaffung einer gut funktionierenden Demokratie betrachtete und glaubte, Mathematiker seien verpflichtet, Menschen zu machen begann es zu benutzen.

Aber selbst in einem Werk von 1940 könnte die RS für immer dort bleiben, wenn 1946 jemand Harold Scott MacDonald Coxeter keine kurze Rezension dieser Arbeit für die relativ neue Zeitschrift American Mathematical Reviews schrieb. In seiner Rezension werden die in der Arbeit erwähnten Polyeder aufgelistet, da ein Naturforscher neue Arten auflisten kann, die er auf einer Expedition entdeckt hat. Die Hauptsache ist, dass er dort das „bemerkenswerte rhombische Hexaeder“ beschrieb und erwähnte, dass „die Form seiner Flächen mit der Form der Flächen der 30-seitigen übereinstimmt, aus denen es durch Angabe einer Sternform erhalten wird“.

Polyeder waren Mitte des 20. Jahrhunderts kein beliebtes Thema in der Mathematik, aber Coxeter war ihr Hauptförderer - und war irgendwie mit jedem verbunden, der sie studierte. 1948 veröffentlichte er das Buch The Right Political Scientists. Es beschreibt systematisch verschiedene Familien von regulären Polyedern, insbesondere das große sternförmige dreißigseitige Polyeder, das tatsächlich ein RS enthält:



Aber in seinem Buch erwähnt Coxeter RS ​​nicht ausdrücklich, und obwohl er mit den Referenzen einiger Polyederliebhaber geehrt wurde, war RS weiterhin wenig bekannt.

Quasikristalle

Kristalle waren schon immer wichtige Beispiele für Polyeder in der Natur. Aber im 19. Jahrhundert, als die Atomtheorie immer mehr Anerkennung fand, begannen die Wissenschaftler, immer ernsthaftere Forschungen auf dem Gebiet der Kristallographie und der Anordnung von Atomen in Kristallen durchzuführen. Polyeder tauchten häufig auf, insbesondere in Darstellungen der Geometrie sich wiederholender Atomblöcke („Zellen“) in Kristallen.

Bis 1850 war bekannt, dass es nur 14 solcher Geometrien geben kann - darunter auch eine, die auf dem rhombischen Dodekaeder basiert. Sie zeichnen sich durch Symmetrien zweiter, dritter, vierter oder sechster Ordnung aus - was im Wesentlichen darauf zurückzuführen ist, dass der Raum nur mit bestimmten Polyedern gefüllt werden kann, genau wie nur reguläre Polygone wie Quadrate eine zweidimensionale Ebene füllen können. Dreiecke und Sechsecke.

Was ist mit anderen, nicht kristallinen Materialien - wie Flüssigkeiten oder Glas? Seit Beginn des 20. Jahrhunderts haben sich die Menschen für die Möglichkeit interessiert, dass dort mindestens ungefähre Symmetrien fünfter Ordnung vorhanden sind. Es ist nicht möglich, den Raum mit den richtigen Ikosaedern zu füllen, aber es kann möglich sein, zwanzigseitige Raumabschnitte mit kleinen Lücken zwischen ihnen zu erstellen.

Diese Frage blieb bis in die 1980er Jahre ungelöst, als die Elektronenbeugungskristallographie unter Verwendung einer schnell abgekühlten Legierung aus Aluminium und Mangan das Vorhandensein einer fünffachen Symmetrie zeigte. Es gab bereits Theorien, um eine solche Symmetrie zu erreichen, und nach einigen Jahren erschienen auch Bilder, die mit einem Elektronenmikroskop aufgenommen wurden und auf denen Teilchen mit der Form eines rhombischen Dreiecks sichtbar waren:



Und während sich die Leute vorstellten, wie diese dreißig Heptaeder miteinander kombiniert werden könnten, erschien ein rhombisches Sixta-Hexa - in Form eines „Lochs“ in einer Gruppe von 12 rhombischen Trihedern:



Zuerst wurde es ein 20-spitzer Stern genannt. Aber dann wurde es mit Beschreibungen in der Literatur über das Polyeder assoziiert und als RS identifiziert.

In der Zwischenzeit wurde die Idee, Objekte aus rhombischen Elementen zu erstellen, immer beliebter. Michael Longe Higgins, Ozeanograph und Experte für Ozeanwellenbildung, schloss sich dem Massenhobby an und patentierte 1987 ein Spielzeug auf der Basis rhomboedrischer Elemente, aus dem ein „Kepler-Stern“ (RS) oder ein „Kepler-Ball“ (rhombische Dreißig) zusammengesetzt werden konnte ):



Und - obwohl ich erst jetzt davon erfahren habe - die rhomboedrischen Blöcke, die wir 2009 als Option für die Erstellung von „Shipastiks“ in Betracht gezogen haben, wurden tatsächlich von der Firma Dextro Mathematical Toys (Rhombo.com) hergestellt, die am Fuße von Longge-Higgins in San arbeitete Diego

Das Problem, den Raum erfolgreich mit dreidimensionalen Figuren zu füllen - oder sogar eine Ebene mit zweidimensionalen Figuren - ist ziemlich kompliziert. Seit den 1960er Jahren ist bekannt, dass im allgemeinen Fall das Problem, ob ein bestimmter Satz von Formularen eine Ebene füllen kann, unlösbar ist. (Grundsätzlich kann geprüft werden, ob 1000 dieser Formulare miteinander zusammengesetzt werden können. Je mehr Formulare wir berücksichtigen, desto mehr Rechenressourcen werden dafür benötigt.)

Leute wie Kepler gingen wahrscheinlich davon aus, dass wenn eine Reihe von Formen eine Ebene füllen könnte, dies als sich wiederholendes Muster erfolgen könnte. Nachdem jedoch klar wurde, dass dieses Problem im allgemeinen Fall nicht gelöst wurde, entwickelte Roger Penrose 1974 zwei Formulare, mit denen das Flugzeug gefüllt werden kann, ohne dass sich Muster wiederholen. Bis 1976 hatten Penrose (und Robert Ammann) eine vereinfachte Version dieser Formulare entwickelt:



Und ja, diese Formen sehen aus wie Rauten, wenn auch nicht wie Gold. Mit Winkeln von 36 °, 144 ° und 72 °, 108 ° haben sie jedoch eine 5-fache und eine 10-fache Symmetrie.

Diese Rauten können keine sich wiederholenden Muster auslegen. Es stellt sich jedoch heraus, dass sie ein systematisch verschachteltes Muster erstellen können:



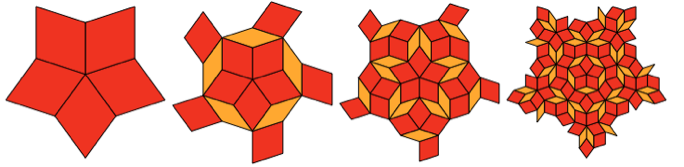
Und ja, der mittlere Teil des 3. Schritts ist dem abgeflachten Shipastik sehr ähnlich. Aber es stimmt nicht ganz damit überein, externe Rauten haben ein etwas anderes Format.

Es besteht jedoch weiterhin eine enge Verbindung zwischen ihnen. Stellen Sie sich vor, wir starten nicht von einer Ebene aus, sondern von einem halben dreidimensionalen rhombischen Dreißigquadrat, das aus goldenen Rauten besteht:



Von oben sieht es genauso aus wie der Beginn des verschachtelten Penrose-Mosaikdesigns. Wenn wir diesen Prozess fortsetzen, erhalten wir dieses Mosaik:



Wenn Sie es „von der Seite“ betrachten, können Sie sehen, dass es sich immer noch um dieselben goldenen Rauten handelt:



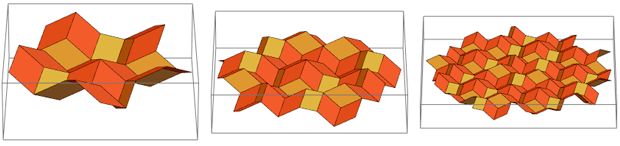
Wenn Sie vier dieser „Wieringa-Dächer“ zusammengestellt haben, erhalten Sie nur RS:



Welche Beziehung besteht zwischen diesen eingebetteten Strukturen und der tatsächlichen Art der Bildung physikalischer Quasikristalle? Es ist noch nicht klar. Es ist jedoch sehr interessant zu sehen, wie Hinweise auf RS in der Natur erscheinen.

Historisch gesehen war es Sandor Kabaei zu verdanken, dass er dank der Diskussion über Quasikristalle begann, RS mit Mathematica zu studieren, was Eric Weinstein dazu brachte, sie zu entdecken, was dazu führte, dass sie in Mathematica und Wolfram Language aufgenommen wurden, was mich dazu veranlasste, einen von ihnen für unser Logo auszuwählen. Zu diesem Zweck drucken wir ein Penrose-Mosaik in unsere Paper Shipastik:

Flachendorn

Unsere Shipastik für Wolfram | Alpha ist 2009 mit der Veröffentlichung von Wolfram | Alpha in die Welt gekommen. Wir haben aber auch unsere Shipastik für Mathematica, die sich seit langer Zeit entwickelt und weiterentwickelt. Als wir 2011 unser neues europäisches Hauptquartier errichteten, kämpften zwei Shipastiks um die Präsenz.

Unser langjähriger Art Director Jeremy Davis hat sich Folgendes ausgedacht: Nehmen Sie einen der Shipastiks und „idealisieren“ Sie ihn nur mit seinem „Skelett“. Die Entscheidung, mit RS zu beginnen, war einfach. Aber dann haben wir es abgeflacht und so erschien die erste Version des jetzt bekannten Logos:

Brasilianische Überraschung

Als ich diesen Artikel begann, dachte ich, dass die ganze Geschichte dort enden würde. Immerhin habe ich bereits beschrieben, wie wir uns für RS entschieden haben und wie Mathematiker darauf gekommen sind. Aber bevor ich mit dem Schreiben fertig war, entschied ich: "Ich werde all die Jahre über alle Briefe über Shipastik durchsehen, um sicherzugehen, dass ich nichts verpasst habe."

Und dann bemerkte ich eine E-Mail der brasilianischen Künstlerin Yolanda Kipriano vom Juni 2009. Sie schrieb, dass sie einen Artikel über Wolfram | Alpha in einem brasilianischen Nachrichtenmagazin gesehen, auf Shipastika aufmerksam gemacht und einen Link zu ihrer Website bereitgestellt habe. Seitdem sind mehr als 9 Jahre vergangen, aber ich bin diesem Link immer noch gefolgt und war erstaunt, Folgendes zu sehen:



Ich las ihren Brief weiter: „In Brasilien heißt dieses Objekt Giramundos oder die„ Mandakaru-Blume “und besteht aus Servietten als künstlerische Verzierung.“

Was ?! In Brasilien gibt es eine Tradition, die mit Shipastik verbunden ist, und seit all den Jahren haben wir nichts davon gehört? Bald entdeckte ich seine Bilder im Netz. Ein kleiner Teil der Modelle bestand aus Papier, der größte Teil aus Stoff - aber es gab viele davon:



Ich schrieb an meinen brasilianischen Freund, der an den ersten Versionen von Wolfram | Alpha arbeitete. Er antwortete schnell: „Diese Objekte kommen mir wirklich bekannt vor. Zu meiner Schande hatte ich nicht genug Lust, zwei und zwei zu vergleichen “, und schickte mir Bilder aus dem lokalen Katalog von Kunstwerken und Kunsthandwerk:



Die Jagd begann: Was waren diese Objekte und woher kamen sie? Jemand aus unserer Firma sagte, dass seine Urgroßmutter aus Chile solche Dinge gehäkelt und sie immer zu einem Schwanz gemacht habe. Wir haben angefangen, mit Leuten in Kontakt zu treten, die Bilder von „Folk Shipastiks“ ins Netz gestellt haben. Sehr oft stellte sich heraus, dass sie ihre Kopien in Geschäften kauften. Aber manchmal sagten die Leute, sie wüssten, wie man sie herstellt. Und alle hatten fast die gleiche Geschichte: Das haben sie von ihren Großmüttern gelernt.

Ein typischer Weg, um - zumindest in unserer Zeit - Volksspitzen zu sammeln, besteht darin, 60 Diamanten aus Pappe zu schneiden. Dann muss jeder in Stoff gewickelt und zusammengenäht werden:



Aber dann entsteht sofort ein mathematisches Problem. Markieren und schnitzen diese Personen goldene Rauten mit einem Winkel von 63 ° korrekt? Normalerweise nicht. Sie stellen Rauten mit 60 ° aus Paaren gleichseitiger Dreiecke her - dies ist die Standard-Rhomboidform, die bei der Herstellung von Quilts verwendet wird. Wie kommen die Thornies zustande? Nun, der Unterschied zwischen 60 ° und 63 ° ist gering. Wenn Sie die Flächen zusammennähen, ist zwischen ihnen genügend Platz zum Manövrieren. Es ist also recht einfach, ein Polyeder herzustellen, ohne absolut genaue Winkel zu erzielen. (Es gibt auch Quasi-Shipastiks, bei denen wie beim Bau von Unkelbach anstelle von Gesichtern keine Rauten, sondern scharfe „äußere Dreiecke“ vorhanden sind).

Spikes im Internet werden unterschiedlich bezeichnet. Meistens - Giramundos. Oft werden sie Estrelas da Felicidade ("Sterne des Glücks") genannt. Die Tatsache, dass sie manchmal als „mährische Sterne“ bezeichnet werden, ist verwirrend, aber tatsächlich sind mährische Sterne viel schärfere Polyeder (meistens aus Rhombokubooktaeder), die in letzter Zeit als Leuchten an Beliebtheit gewonnen haben.

Trotz langwieriger Nachforschungen kenne ich immer noch nicht die gesamte Geschichte der Folk-Spikes. Folgendes habe ich entdeckt.Erstens konzentrieren sich die meisten der heute beliebten Spikes auf Brasilien (obwohl wir Geschichten über ihr Auftreten an anderen Orten haben). Zweitens sieht die Tradition ziemlich alt aus, sie erschien definitiv lange vor dem 20. Jahrhundert und vielleicht einige Jahrhunderte zuvor. Soweit ich das beurteilen kann, wird es von Mund zu Mund weitergegeben, wie es normalerweise bei der Volkskunst der Fall ist, und ich habe keine wirklichen historischen Dokumente zu diesem Thema gefunden.

Die besten Informationen wurden mir von Paula Guerra zur Verfügung gestellt, die in einem von ihr vor zehn Jahren geführten Touristencafé in der historischen Stadt São Luis do Paraiting Volksspitzen verkaufte. Sie sagte, dass Menschen aus ganz Brasilien in ihr Café kamen, Volksspitzen sahen und so etwas wie "Ich habe solche Dinge seit etwa 50 Jahren nicht mehr gesehen."

Paula selbst lernte von einer älteren Frau, die auf einer Familienfarm lebte und sie seit ihrer Kindheit herstellte, etwas über Volksspitzen (sie nennt sie "Sterne") und lernte dies von ihrer Mutter. Ihr Prozess - anscheinend ein typischer - bestand darin, irgendwo Pappe zu sammeln (ursprünglich war es so etwas wie Hutschachteln), die Stücke mit Stoff zu bedecken und sie zusammenzunähen, um ein Objekt von etwa 15 cm Größe zu erhalten.

Wie alt ist ein Volksstachel? Dies kann nur durch mündliche Überlieferung gewürdigt werden. Wir fanden mehrere Leute, die sahen, wie Shipastiks von ihren Verwandten hergestellt wurden, die im Gebiet von 1900 geboren wurden. Paula sagte, dass sie sich vor zehn Jahren mit einer 80-jährigen Frau getroffen habe, die ihr erzählte, dass es als sie vor 200 Jahren auf einer Kaffeefarm aufwuchs, ein ganzes Regal gab, in dem von vier Generationen von Frauen Volksspitzen hergestellt wurden.

Ein Teil der Geschichte der nationalen Shipastik scheint sich um Traditionen zu drehen, die von Mutter zu Tochter weitergegeben werden. Es wird gesagt, dass Mütter oft Stacheln als Hochzeitsgeschenke für ihre Töchter machten. Typischerweise wurden Shipastiks aus Kleidungsstücken und anderen Dingen hergestellt, die Töchter an ihre Kindheit erinnern - so etwas wie die Patchwork-Quilts, die heutzutage für Kinder gemacht werden, die aufs College gehen.

Bei Folk-Spikes wurde jedoch eine andere Wendung entdeckt: Oft steckte die Mutter vor dem Nähen eines Spielzeugs Geld ein, das ihre Tochter in kritischen Fällen verwenden konnte. Und die Tochter behielt ihre Shipastik zusammen mit ihren Nähutensilien, wo ihr Mann ihn kaum gefunden hätte. Einige Spikes wurden als Stecknadeln verwendet - was möglicherweise als zusätzliches Hindernis für Ehemänner gedient hat.

Welche Familien unterstützten die Tradition der Herstellung von Volksspitzen? Seit etwa 1750 gibt es in ländlichen Gebieten Brasiliens, weit entfernt von Städten, viele Kaffee- und Zuckerplantagen. Bis etwa zum 20. Jahrhundert brachten Bauern oft Mädchen aus abgelegenen Städten zu ihren Bräuten - oft sehr jung, bis zu 13 Jahre alt. Vielleicht trugen diese Bräute - normalerweise aus guten Familien portugiesischer Abstammung mit relativ guter Ausbildung - Volksdorn.

Anscheinend verbreitete sich die Tradition im Laufe der Zeit auf die schlechteren Familien und blieb im Grunde dort. Aber irgendwo in der Mitte des 20. Jahrhunderts - wahrscheinlich als Straßen im Land auftauchten, die Urbanisierung begann und die Menschen anfingen, Bauernhöfe zu verlassen - starb die Tradition fast aus. In den ländlichen Schulen in Südbrasilien wurden Mädchen in den 1950er Jahren im Kunstunterricht unterrichtet, um Folk-Spikes mit einem speziellen Steckplatz für Sparschweine herzustellen.

Volksspitzen haben in verschiedenen Teilen Brasiliens eine unterschiedliche Geschichte. In den südlichen Grenzregionen (in der Nähe von Argentinien und Uruguay) gibt es eine Tradition, nach der „der Stern von St. Miguel “(sie ist auch eine Volksschiffastik) wurde in Dörfern von Heilerinnen (dh„ Hexen “) hergestellt, die bei der Herstellung von Spielzeug über die Gesundheit der Patientin nachdenken mussten.

In anderen Teilen Brasiliens wurden Spielzeuge oft als Blumen- und Fruchtnamen bezeichnet, die ihr leicht ähnelten. Im Nordosten - Flor Mandacarú (mit dem Namen der Kaktusblüten). In tropischen Feuchtgebieten - Carambola (zu Ehren der Carambola-Früchte, manchmal auch "tropische Sterne" genannt). In den zentralen Waldgebieten - Pindaíva (zu Ehren der roten, stacheligen Frucht).



Aber meistens heißt die beliebte Shipastika Giramundo, ein ziemlich altes portugiesisches Wort, das wörtlich "wirbelnde Welt" bedeutet. Anscheinend wurden die Spielzeuge als Amulette verwendet, die mit ihrer Rotation im Wind viel Glück bringen. Vor kurzem wurden Schwänze an ihnen befestigt, aber anscheinend war es üblich, sie in Häusern aufzuhängen, möglicherweise an Feiertagen.

Es ist oft unklar, welche der Traditionen, aus denen die Shipastika hervorging, ursprünglich war und welche kürzlich erschienen sind. Bei der Dreikönigstagsparade (der lokale Name ist „der Tag der drei Könige“) in São Luis do Paraiting wurden Volksspitzen als Symbol für den Stern von Bethlehem verwendet - aber dies ist anscheinend keine sehr alte Tradition und zeigt eindeutig keine Zusammenhänge mit der Religion.

Wir fanden mehrere Beispiele für Folk-Spikes, die auf Kunstausstellungen auftraten. Eine davon, die 1963 stattfand und der Volkskunst im Nordosten Brasiliens gewidmet war, wurde von der Architektin Liina bo Bardi organisiert. Die andere, in der die größte der dreidimensionalen Spitzen ausgestellt wurde, die ich gesehen habe, wurde 1997 vom Architekten und Designer Vladavio Imperio organisiert:



Woher kamen also die Volksspitzen? Ich weiß das immer noch nicht. Sie könnten in Brasilien auftreten, sie könnten aus Portugal oder einem anderen Teil Europas kommen. Die Tatsache, dass sie Stoffstücke verwendeten und für ihre Herstellung nähten, könnte ein Argument für ihre afrikanische oder indianische Herkunft sein.

Eine moderne Handwerkerin, die Shipastiks herstellt, sagte, ihre Urgroßmutter, die solche Spielzeuge herstellte und Ende des 19. Jahrhunderts geboren wurde, stamme aus einer Region Italiens namens Romagna (und eine sagte, sie habe gelernt, Shipastiks von ihrer Großmutter herzustellen, die aus französischen Kanadiern stammte). Ich denke, es ist durchaus möglich, dass Volksspitzen früher in Europa verbreitet waren, aber vor vielen Generationen ausgestorben sind, und diese Tradition hat dort nicht überlebt. Und obwohl in europäischen Gemälden vergangener Jahrhunderte ziemlich viele verschiedene Polyeder vorkommen, sind mir keine Bilder von Shipastik unter ihnen bekannt (auch ich habe Shipastik in der islamischen Kunst nicht gesehen).

Aber ich bin mir ziemlich sicher, dass Folk-Spikes einen Ursprung haben. So etwas wäre kaum zweimal erfunden worden.

Ich muss sagen, dass dies nicht meine erste Jagd auf dem Gebiet der Kunst ist. Die Suche nach dem ersten eingebetteten Muster ( Sierpinski ) erwies sich als erfolgreicher - was mich schließlich zur Krypta in der italienischen Kirche führte, wo ich anhand eines Beispiels eines Steinmosaiks aus dem 13. Jahrhundert beobachtete, wie dieses Muster allmählich entdeckt wurde.

Bisher hat Shipastik nicht so leicht aufgegeben - und die Situation wird dadurch erschwert, dass es im Grunde genommen aus Stoff hergestellt wurde, der nicht so gut wie Stein bleibt.

Spikes werden lebendig

Unabhängig von seiner Herkunft spielt Shipastik die Rolle eines starken und würdigen Logos. Aber manchmal macht es Spaß, die Shipastik wiederzubeleben - und im Laufe der Jahre haben wir aus verschiedenen Gründen verschiedene personalisierte Shipastiks hergestellt:



Bei Verwendung von Wolfram | Alpha zeigt das System normalerweise eine geometrische Shipastik an. Aber manchmal animiert Ihre Anfrage es - zum Beispiel Anfragen nach π am Pi-Tag:

blog.stephenwolfram.com/data/uploads/2018/12/spikey-lives-happy-pi-day-video.mp4

Spikes für immer

Polyeder sind ewig. Sie sind auf dem Bild von vor 500 Jahren zu sehen, das so klar und modern aussieht wie das Polyeder auf meinem Computer.

Ich habe viel Zeit damit verbracht, nach abstrakten Computer-Dingen zu suchen (zum Beispiel nach zellularen Automaten). Sie haben auch etwas Zeitlosigkeit. Aber für sie habe ich keine historischen Beweise gefunden. Wie abstrakte Objekte können sie jederzeit erstellt werden. Aber sie sind heute dank unserer konzeptionellen Plattformen und Tools erschienen - und niemand hat sie zuvor gesehen.

Die reiche Geschichte und Beständigkeit der Polyeder ist Tausende von Jahren alt. Im Aussehen ähneln sie Edelsteinen. Das Finden des richtigen Polyeders einer bestimmten Art ist wie das Finden eines Edelsteins in einem geometrischen Universum aller möglichen Formen.



RS ist einer dieser erstaunlichen Steine, und als ich seine Eigenschaften studierte, begann ich ihn noch mehr zu schätzen. Aber es ist auch ein Juwel mit einer menschlichen Geschichte - und es ist schrecklich interessant zu sehen, wie eine solche Abstraktion wie ein Polyeder Menschen aus der ganzen Welt mit einer so unterschiedlichen Geschichte und Zielen verbinden kann.

Wer hat als erster das rhombische Hexaeder erfunden? Wir wissen es nicht und werden es vielleicht nie erfahren. Aber jetzt, wo wir es haben, wird er für immer bei uns bleiben. Mein Lieblingspolyeder.