Frühlingszivilisation, 1/5

### Teil 1. Goldenes "Ku"

Mit ungefähr sechs Jahren fiel ich auf Lastwagen der Mitte des 20. Jahrhunderts in die Hände eines Großvaters ^[50] . Solide, gedruckt auf glattem, dickem Papier, seltenes Buch. Das einzige, was meinem Großvater nach dem Zusammenbruch des Landes, Kriegen und Reisen noch in Erinnerung geblieben ist.



Das Nachschlagewerk enthielt viele interessante Leistungsmerkmale, so dass mir das Wort "Belastbarkeit" von früher Kindheit an bekannt wurde. Und als mein Vater auf einem Spaziergang erwähnte, dass jeder Lastwagen so viel wiegt wie er selbst, erinnere ich mich daran. Er erinnerte sich und wurde viel später interessiert.

Vater hatte recht. Für Lastwagen der 60er Jahre wird diese Regel mit überraschender Genauigkeit umgesetzt:



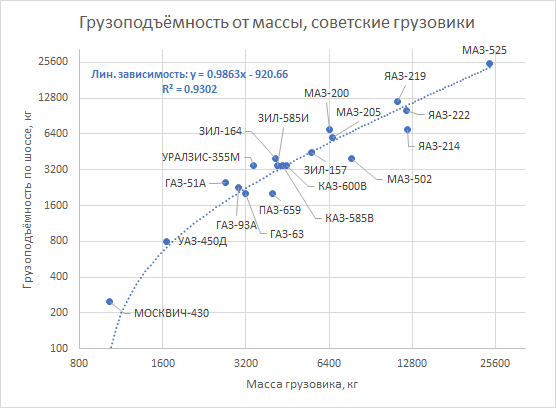
Es ist viel merkwürdiger, dass dieses Muster auch bei Fahrzeugen beobachtet wird, die völlig anders sind als Lastwagen.

Zuerst habe ich zum Spaß Frachtflugzeuge auf den Plan gesetzt. Und war überrascht. Ich fing an, andere Fahrzeuge hinzuzufügen. Reiten, schwimmen und fliegen, gebaut in den Jahrhunderten des 19., 20. und 21. Jahrhunderts, arbeitet an der Energie von Wärme, Atom, Wind und sogar Pferd. Ergebnis? Schwache Leistung (Indikator 1.125), wenn nicht nur lineare Abhängigkeit. Auf Massen von Hunderten von Kilogramm bis sechzigtausend Tonnen. Bei Abweichungen natürlich, wohin könnte man ohne sie gehen, manchmal bis zu zehnmal, aber bei sechs Massenordnungen ist dies offensichtlich eine Kleinigkeit.

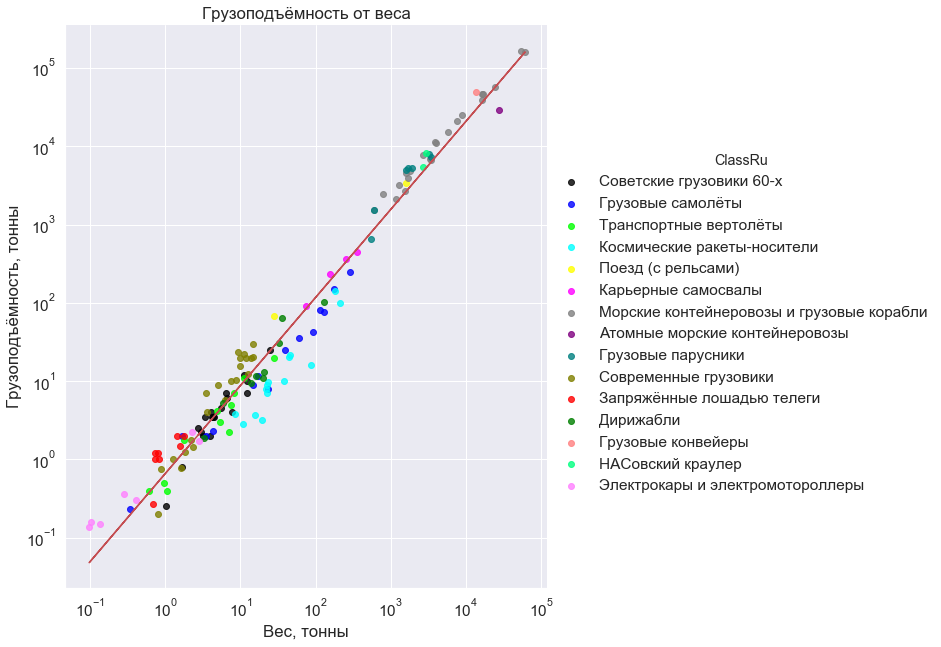
Hier ist es diese Abhängigkeit, die sich auf die Diagonale eines riesigen leeren Feldes drückt:


Auf der Karte vermerkt: Frachtflugzeuge; Transporthubschrauber; Luftschiffe, modernes und frühes Jahrhundert; Trägerraketen (in niedriger Umlaufbahn); Sowjetische Lastwagen der 60er Jahre; moderne Bergbau-LKWs; moderne Lastwagen aus Russland, den USA, China und Indien; Elektroautos und Motorroller; Züge (mit Schienen); nukleare Containerschiffe; Containerschiffe und Frachtschiffe (keine Tanker); Segelfrachtschiffe von 17 bis 20 Jahrhunderten; Förderbänder für die Erzübertragung; Nassovsky Traktor für den Export von Raketen zum Start; und schließlich Pferdewagen.

Wenn Sie den Wert Q eingeben, der als Masse der transportierten Fracht im Verhältnis zur Trockenmasse des Fahrzeugs definiert ist, sieht dies für jede der Gruppen folgendermaßen aus:



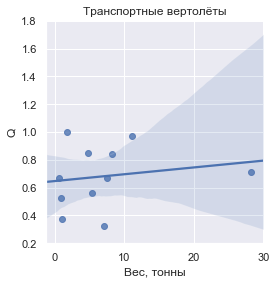
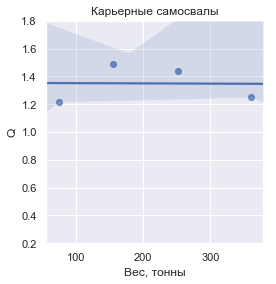
In Zahlen sind die Q- Werte:

Anlageklasse	Durchschnittliches Q.	Standardabweichung Q.
Frachtflugzeug	0,667091	± 0,206162
Transporthubschrauber	0,681605	± 0,225062
Luftschiffe, modern und frühes Jahrhundert	0,842673	± 0,374622
Trägerraketen (niedrige Umlaufbahn)	0,372446	± 0,155810
Sowjetische Lastwagen der 60er Jahre	0,777435	± 0,232425
Moderne Bergbau-LKWs	1,349610	± 0,136840
Moderne Lastwagen von Russland, USA, Indien, China	1,293679	± 0,604313
Elektrokarten und Roller	1,098433	± 0,343791
Zug (mit Schienen)	2,275989	± 0,205999
Nuklearcontainerschiff	1,035233	± NA
Seecontainerschiffe und Frachtschiffe (keine Tanker)	2,556004	± 0,378040
Segelfrachtschiffe von 17-20 Jahrhunderten	2.488461	± 0,671785
Frachtförderbänder	3,703704	± NA
Nasovsky Traktor für den Start von Raketen	2,355919	± 0,525174
Pferdewagen	1.203061	± 0,389183

Wie zu sehen ist, ist Q zwar nicht überall streng singulär, sondern tendiert innerhalb jeder Gruppe zu einem gemeinsamen Wert nahe der Einheit.


Es kam mir ... mysteriös vor. Warum erhöhen ein hölzernes Segelboot, ein Aluminium-Elektroauto und ein Atomcontainerschiff mit hunderttausend Elektroautos mehr oder weniger ihr Gewicht? Was bringt uns dazu, Fahrzeuge mit der Qualität Q ≈ 1 für tausende Male unterschiedliche Massen herzustellen? Ist dies eine Manifestation der Eigenschaften der Weltphysik, der terrestrischen Wirtschaft, ist es eine Einschränkung der menschlichen Intelligenz? Wie universell ist dieses Gesetz, wird es für Zivilisationen anderer Sterne umgesetzt? Globale Probleme. Es ist unwahrscheinlich, dass sie hier und jetzt gelöst werden. Aber hier ist es möglich und notwendig zu überlegen und zu beißen, wie viel es werden wird. Das werden wir tun.

Der Weltrekord ^{[ 180 ] beim} Heben einer Langhantel durch eine Person mit durchschnittlichem Gewicht liegt über 200 kg. Theoretisch bedeutet dies, dass unser Körper einen Sicherheitsspielraum für Rucklasten von mindestens bis zu Q = 2,5 hat. Dies erfordert jedoch solch exorbitante Kräfte und Training, dass es niemals in alltäglichen Aktivitäten eingesetzt wird. Es ist ratsamer, Zucker in Säcken von 50 Kilogramm zu verpacken, obwohl dies viermal mehr Lader oder einen Walker erfordert. Beachten Sie, dass diese Situation das Ergebnis der biologischen Evolution ist, an der der menschliche Intellekt (fast) nicht teilgenommen hat und daher ein „Alibi“ enthält.

Physik und Technik allein verbieten keine hohen Qs. Es gibt eine Wasserstoffturbopumpe für das Shuttle-Mitteltriebwerk, das kleine kleine Ding auf dem Bild rechts, das eine Leistung von 54 Megawatt ^{[ 60 ]} bei einem Gesamtgewicht von 350 kg entwickelt:

[Bildnachweis: [ 10 ]]

Wenn zur Vereinfachung Q nach Leistung pro Kilogramm Masse bewertet wird, ist dies 100-mal höher als bei einem anständigen Auto. Aber dieses Ding ist fast wie eine Rakete! Es ist billiger, 100 Autos mit Q = 1 herzustellen und die Fracht mit ihnen zu transportieren, als zu versuchen, diese Einheit auf einem Rollwagen zu „nutzen“.

Solche Überlegungen legen nahe, dass die Gründe hier wirtschaftlicher Natur sind. Darüber hinaus nicht im engeren Sinne spezifischer Volkswirtschaften und Länder (weil unsere Geräte von sehr unterschiedlichen Völkern und Systemen erzeugt werden), sondern im Sinne von "Zweckmäßigkeit der Bemühungen". Die Angemessenheit ist universell genug, um anscheinend für sehr unterschiedliche Produkte und irgendwo sogar für Tiere zu gelten.

_{Der Artikel wurde für die Website https://habr.com geschrieben . Bitte beachten Sie beim Kopieren die Quelle. Der Autor des Artikels ist Evgeny Bobukh .}

Versuchen wir, die Grenzen dieser Zweckmäßigkeit quantitativ zu untersuchen. Wir stellen die Frage: Wie hängen die Kosten eines Geräts mit fester Masse von Q ab ? Hier gibt es zum Beispiel einen 10 Tonnen schweren Muldenkipper, der 10 Tonnen Fracht aufnimmt. Wir wollen auch 10 Tonnen machen, aber 20 Tonnen ( Q = 2) oder sogar 50 ( Q = 5) wegnehmen. Auf dem gleichen Stand der Technologieentwicklung, dem gleichen Produktionsvolumen. Es ist klar, dass höhere Lasten die Anforderungen an Materialien (Stahl -> Titan?) Und an Motoren (andere Temperaturen, Drücke) und an die Technik (weniger Fehlertoleranzen, schwierigere Konstruktionen) erhöhen. Wenn Q wächst, wird natürlich alles teurer. Aber wie oft im Vergleich zu den zehn Tonnen?

Diese Aufgabe ist natürlich nicht trivial. Dennoch können einige Schätzungen dafür aus den allgemeinsten Überlegungen erhalten werden. Was wir jetzt tun werden.

Wir führen die Funktion C ( Q ) ein. Es beschreibt die niedrigstmöglichen Kosten eines Geräts mit einem Wirkungsgrad von Q , ausgedrückt in den Kosten eines ähnlichen Geräts mit der gleichen Masse bei Q = 1. Was ist darüber bekannt?

1. C (1) = 1 per Definition.

2. C ( Q ) ist eine stetige Funktion, zumindest bis die Massendifferenz durch Stückatome gemessen wird. Intuitiv scheint es glatt genug zu sein, um die ersten Derivate zu haben. Ich denke, wir können (wie bei den meisten physischen Funktionen) zugeben, dass es im Allgemeinen analytisch ist.

3. C ( Q ) ist eine streng ansteigende Funktion. Je höher die Qualität von Q ist , desto schwieriger ist es, die Struktur herzustellen, und desto teurer ist sie. Das heißt, dC ( Q ) / dQ > 0 zumindest für Q > 0.

4. Wenn Q größer als ungefähr 3 ist, beginnt C ( Q ) schneller als linear anzusteigen. Warum? Weil wir sehen, dass es für Menschen billiger ist, drei Lastwagen für zehn Tonnen mit Q = 1 als einen für dreißig mit Q = 3 herzustellen. Zusammenfassend schreiben wir: k * C (1) < C ( k ) für k > ≈3 - andere in Worten, C ( k ) wächst schneller als k für k > ≈3.

5. Da zehn Flugzeuge mit Q = 0,1 eindeutig unwirtschaftlich sind als eines mit Q = 1 (weil sie das zweite und nicht das erste bauen), gilt für k > ≈3: k * C (1 / k )> C (1), oder C (1 / k )> 1 / k .

6. Die Kosten der Pumpe aus dem Shuttle deuten darauf hin, dass der Wert von C ( Q ) als Exponent mit einem signifikanten Indikator mindestens bis zu Q ~ 100 nicht ansteigt. Andernfalls würde diese TNA nicht Millionen von Dollar kosten, sondern eine Art von 10 ²⁰ Dollar, und wir hätten es kaum geschafft. Das heißt, C (100) liegt irgendwo zwischen 10 ³ - 10 ⁸ , aber überhaupt nicht 10 ¹⁵ .

7. Was ist C (0) gleich? Dies sind die Kosten für das Gerät, das sich zwar selbst bewegen kann, aber keine Fracht wegnehmen kann. Offensichtlich ist ein solcher "LKW" billiger als ein voller LKW. Aber wie oft? Die Geschichte zeigt, dass manchmal eher als zehn oder Hunderte. Etwa 15 Jahre sind vom ersten Flugzeug, das nur sich selbst bewegen kann ( Q = 0), bis zum Warentransport auf dem Luftweg vergangen. Von den ersten Benzinwagen bis zu recht anständigen Lastwagen mit Q = 1,5 ([ 120 ] + [ 130 ]) etwas mehr. Wenn diese Entwicklung eine unglaubliche Komplexität gewesen wäre, wäre sie kaum so schnell abgeschlossen worden. Folglich sollten sich die Schwierigkeit der Herstellung und die Kosten eines Fahrzeugs mit Q = 0 nicht grundlegend von denen für Q = 1 unterscheiden. Daher erwarten wir, dass C ( 0 ) irgendwo zwischen 0,1 und 0,5 liegt.

8. Ist diese Funktion für negatives Q sinnvoll? Ganz! Ein LKW mit Q = -0,5 bewegt sich nur, wenn Sie die Hälfte seines Gewichts von einem Turmdrehkran entfernen. Und Q = -1 - dies ist ein Wagen, der keine Traktion entwickelt. Kann Fracht nur transportieren, wenn Sie sie im Schlepptau nehmen. Das heißt, im Allgemeinen ohne Motor. Offensichtlich sind seine Kosten, wenn nicht ungleich Null, sehr gering. Setzen Sie daher C (-1) ≈ 0.

9. Und was ist C (-2)? Dies sind die Kosten für ein Gerät, das mit mindestens dem doppelten Gewicht hochgezogen werden muss, um sich zu bewegen! Ja, Bereiche Q <-1 sind Anker, Fundamente, Pfähle, Bremsen. Geräte, die die Bewegung behindern. Dort gibt es natürlich eine völlig andere Dynamik und ihre eigenen Gesetze, aber zumindest sehen wir, dass C ( Q ) nicht mit einer Singularität bei Q <-1 endet und dass es in der Region Q = -1 ein Minimum hat und daher zumindest Eine kleine Nachbarschaft dieses Punktes C ( Q ) sollte sich wie eine Parabel verhalten.

Das skizzenhafte C ( Q ) sieht also ungefähr so ​​aus:


Wir erweitern C ( Q ) in einer Taylor-Reihe am Punkt Q = -1:



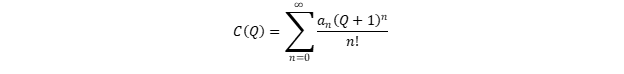
Aus Eigenschaft (8) folgt, dass a ₀ = 0. Die Eigenschaften (4), (5) und teilweise (9) deuten darauf hin, dass eine ₁ nahe Null ist oder dass ihr Beitrag in jedem Fall nicht im Bereich 0 dominiert. .3.

Und dann stellt sich heraus, dass der erste Nicht-Null-Term bei der Expansion von C ( Q ) parabolisch ist und dass sich für Q im Bereich der Einheiten C ( Q ) ungefähr wie eine quadratische oder etwas schneller ansteigende Funktion verhält:

C ( Q ) ≤ a ₂ * ( Q + 1 ) 2/2 + O (( Q + 1 ) ³ )

Und aus [1] folgt, dass a ₂ ≈ 1/2.

Da die Funktion C ( Q ) mindestens bis zu Q ~ 100 immer noch nicht exponentiell ist (Eigenschaft (6)), können wir sie dort gleich Q ^p mit dem Exponenten p irgendwo im Bereich von 2 ... 4 setzen. Kaum mehr.

Schlussfolgerung: Bei einer festen Masse steigen die Kosten der Vorrichtung C (Q) nicht schwächer als (Q + 1) 2/4, sondern nicht schneller als etwa O (Q ⁴ ) [1].

Ist es möglich, die tatsächliche Abhängigkeit von C ( Q ) zu betrachten, um zu verstehen, wie richtig diese Schlussfolgerung ist? Es ist schwer. Die meisten Mechanismen, die der Mensch herstellt, sind unterschiedliche Massen, aber festes Q im Bereich der Einheit. Wir brauchen das Gegenteil: ungefähr die gleiche Masse, aber unterschiedliche Q. Anfangs hatte ich auf Daten zu Flugzeugtriebwerken gehofft ... aber die Arbeit ^{[ 70 ] [ 80 ]} an deren Preisgestaltung ist sehr lustig. Dort werden die Motorpreise klassifiziert und nur Formeln für Vorhersagen und Durchschnittsfehler veröffentlicht.

Glücklicherweise kam Hilfe von Autos ^{[ 150 ]} . Mit ihnen, mit ungefähr der gleichen Masse, werden Motoren mit verschiedenen Kapazitäten gefunden. Und obwohl Strom noch keine transportable Fracht ist, ist er mit einigem technischen Aufwand ungefähr proportional dazu. So können wir abschätzen, ob unsere Formel der Realität nahe kommt.

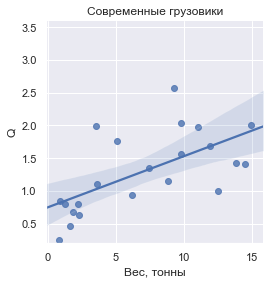
Es scheint ja:

[Quelle: [ 150 ]]

Blaue Punkte sind echte Autos. In erster Näherung steigt ihr Preis als Leistungsdichte im Grad von 2,3.

Rote Punkte - der nach der Formel [1] berechnete Preis, basierend auf der Annahme, dass Q = 1 den billigsten Autos pro Kilogramm im Bereich von 20 bis 30.000 US-Dollar entspricht. Es ist zu sehen, dass die Formel wirklich eine gute Schätzung von C ( Q ) von unten liefert (wo wir es angestrebt haben).

Wenn man die Masse dieser leckeren Punkte betrachtet, besteht eine starke Versuchung: C ( Q ) durch sie zu ziehen und somit die Abhängigkeit direkt zu untersuchen. Dies ist nicht möglich. Hauptsächlich, weil der Preis eines Personenkraftwagens nicht nur von seinen Traktionseigenschaften bestimmt wird. Es ist kaum vorstellbar, dass ein Auto für hundert Kilobaxen nicht über die beste Klimaanlage, die bequemsten Sitze und den „Platin-Aschenbecher mit rhodinierter Lünette“ verfügt. Und das alles kostet Geld, das nichts mit unserem C ( Q ) zu tun hat. Hier sieht jedoch der untere „Zweig“ von Autos interessant aus, der fast genau nach dem berechneten C ( Q ) fährt. Ich wage zuzugeben, dass dies nur Autos ohne Schnickschnack sind. Wo "nicht Dame, sondern zu gehen." Aber mehr als 100.000 US-Dollar für ein Auto sind nicht mehr da.

_{Der Artikel wurde für die Website https://habr.com geschrieben . Bitte beachten Sie beim Kopieren die Quelle. Der Autor des Artikels ist Evgeny Bobukh .}

So können wir die Kosten von Geräten mit hohem Q zumindest in der Größenordnung abschätzen. Warum war das notwendig?

Aber warum. Schauen Sie sich den ersten Schritt des Raumträgers an. Nun, zumindest Proton-M ^{[ 110 ]} , der Vollständigkeit halber. Sie ist ein fast vollwertiges Fahrzeug mit Motoren, einem Steuerungssystem, einem angemessenen Sicherheitsspielraum und einem Trockengewicht von 31 Tonnen. Gleichzeitig schleppt sie zu Beginn der Rakete nicht nur die Nutzlast, sondern auch den gesamten Treibstoff, alle oberen Stufen und natürlich sich selbst auf ihren Buckel. Insgesamt - 683 Tonnen. Plus Startüberlastung, insgesamt (effektiv) 1068 Tonnen Ladung! Aus der Sicht der ersten Stufe funktioniert es in einem schrecklichen Modus Q = (1068/31) = 34,4! Dies entspricht 50 Tonnen Fracht auf einem Personenkraftwagen.

Und wir wissen, dass die Kosten für ein Gerät mit hohem Q mindestens (Q + 1) 2/4 mal höher sind als bei Q ≈ 1. Für Proton beträgt dies ... das 313-fache.

Das heißt, der Proton sollte 300-mal mehr kosten als ein ähnliches Gerät mit Q = 1. Und diese Zahl ist wenig abhängig von Fortschritt und Technologie. Denn sobald die "britischen Wissenschaftler" eine Superlegierung erfinden, die eine Rakete billiger macht, werden auch Bodenmotoren billiger. Daher ist eine chemische Rakete, auch wenn sie wiederverwendbar ist, immer sehr teuer. Mag es oder nicht.

Gut. Sagen wir 300 mal. Aber verglichen mit was ? Wäre es schön, unsere Berechnungen mit einigen objektiv vorhandenen Geräten zu vergleichen, um grobe Fehler zu vermeiden?

Leider gibt es keine 30-Tonnen-Raketen mit Q = 1. Es gibt jedoch ungefähre Analoga, die zum Vergleich geeignet sind:

• Der allererste ist ein Bergbau-LKW. Ja, keine Rakete. Trotzdem ist es auch eine Wärmekraftmaschine, nicht ganz trivial und eines der billigsten Mittel für den Warentransport. Und wenn wir bereits über Weltraumforschung sprechen, sollte der LKW dann nicht der Prototyp des Geschäftsmodells der Raumkabine sein? Versuchen wir es also, zumindest für eine allgemeine Schätzung. Hier ist ein 30 Tonnen schwerer Belaz-7540. Der Marktpreis ^{[ 140 ]} beträgt 3,7 Millionen Rubel, d.h. 62.000 US-Dollar. Für Proton wird dies in die Kosten der ersten Stufe in der Größenordnung von 19 Millionen US-Dollar umgerechnet. Wikipedia steht für ^{[ 100 ]} Startkosten von 65 Millionen US-Dollar. Ziemlich nah dran, da dieser Betrag viel mehr beinhaltet, außer dem Preis des allerersten Schritts.
• In [ 160 ] wird eine experimentelle Raketenplattform auf Schienen beschrieben. Eine Masse von 10 Tonnen, fünf Stufen, beschleunigt auf 4 km / s. Der Preis beträgt 750 Kilobax. Gemessen an den veröffentlichten Bildern und Parametern arbeitet dieses Gerät irgendwo mit Q = 10. Keine Einheit, aber immer noch nicht 34. Wenn Sie von diesen Zahlen ausgehen, sollte der erste Schritt des Protons irgendwo 23 Millionen Dollar kosten.
• Wenn ich mir eine Rakete mit Q = 1 vorstelle, sehe ich im Allgemeinen eine Art kräftigen Rohling mit einer kleinen Kerbe, die mit Schießpulver gefüllt ist. Schießpulver brennt aus und schiebt den Rohling nach vorne. Ein bisschen beschleunigen Sie nicht so stark. Ich habe dieses Bild zwei Tage lang verschoben, bis mir klar wurde, dass es mich erinnert. Das ist ... ein Drucklufthammer! Wo sich das Gas ausdehnt und den Rohling drückt. Die ultimative Bastardisierung der Idee eines Strahltriebwerks, die immer noch eine Art Verwandtschaft bewahrt. Nun, wir suchen. Ja, hier ist der ^{[ 170 ]} Stanko M212 Drucklufthammer. Das Gewicht der Scheibe beträgt 2 Tonnen, die gesamte Struktur 58,3 Tonnen. Das Q- System ist daher bescheidene 0,034. Verkauft für 40 Tausend Euro. Wenn wir die Kosten dieses Witzes gemäß der Formel [1] auf Q = 34,4 hochrechnen, erhalten wir ... 47 Millionen Euro. Oder 24 Millionen im Verhältnis über 30 Tonnen.

Es scheint, dass wir nicht wirklich von der Realität getrennt sind.

Zusammenfassend. Da Raketen, auch wiederverwendbare, 2 bis 3 Größenordnungen teurer sind als Lastwagen, kostet jede aus bodengestützten Materialien hergestellte Raumsiedlung 100- bis 1000-mal mehr als bodengestützte Gegenstücke. Dies ist eine sehr hohe Entwicklungsbarriere.

Raketen sind teuer, weil sie sehr schwer sind und zur Arbeit gezwungen werden, wenn sie bei hohem Q ungesund sind . Aber warum sind die Raketen schwer? Die Antwort (die etwas tiefer liegt als die Tsiolkovsky-Formel) werden wir im zweiten Teil betrachten.

Fortsetzung folgt .

Update: Mehrere Personen haben versucht, bei der Betrachtung der Raketen auf die Unklarheiten bezüglich des Treibstoffs hinzuweisen. Ich habe darüber nachgedacht. Und mir wurde klar, dass der Artikel wirklich ungenau ist. In den Kommentaren hier gesehen .