Kalman-Filter zur Minimierung des Entropiewertes eines zufälligen Fehlers mit einer nicht-Gaußschen Verteilung

Einführung

Bei Habr wurde in den folgenden Veröffentlichungen eine mathematische Beschreibung des Betriebs des Kalman-Filters und seiner Anwendungsmerkmale berücksichtigt [1 ÷ 10]. In der Veröffentlichung [2] wurde der Algorithmus des Kalman-Filters (FC) im Modell des „Zustandsraums“ in einer einfachen und verständlichen Form betrachtet. Es sollte beachtet werden, dass die Untersuchung von Steuerungs- und Managementsystemen im Zeitbereich unter Verwendung von Zustandsvariablen in letzter Zeit aufgrund der einfachen Analyse in großem Umfang verwendet wurde [11].

Die Veröffentlichung [8] ist speziell für die Ausbildung von großem Interesse. Die methodische Technik des Autors ist sehr effektiv. Er begann seinen Artikel mit der Betrachtung der Verteilung des zufälligen Gaußschen Fehlers, berücksichtigte den FC-Algorithmus und endete mit einer einfachen iterativen Formel zur Auswahl der FC-Verstärkung. Der Autor beschränkte sich auf eine Betrachtung der Gaußschen Verteilung unter Berufung auf die Tatsache, dass für ausreichend große $$$n$ (Mehrfachmessungen) Das Verteilungsgesetz der Summe der Zufallsvariablen tendiert zur Gaußschen Verteilung.

Theoretisch ist eine solche Aussage sicherlich richtig, aber in der Praxis kann die Anzahl der Messungen an jedem Punkt im Bereich nicht sehr groß sein. Kalman RE selbst erhielt Ergebnisse zur minimalen Kovarianz des Filters basierend auf orthogonalen Projektionen, ohne anzunehmen, dass die Messfehler Gaußsch sind [12].

Der Zweck dieser Veröffentlichung ist es, die Fähigkeiten des Kalman-Filters zu untersuchen, um den Entropiewert eines zufälligen Fehlers mit einer nicht-Gaußschen Verteilung zu minimieren.
Um die Wirksamkeit des Kalman-Filters bei der Identifizierung des Verteilungsgesetzes oder einer Überlagerung von Gesetzen aus experimentellen Daten zu bewerten, verwenden wir die Informationstheorie von Messungen, die auf der Informationstheorie von C. Shannon basieren, wonach Informationen wie eine physikalische Größe gemessen und bewertet werden können.

Der Hauptvorteil des Informationsansatzes zur Beschreibung von Messungen besteht darin, dass die Größe des Entropieintervalls der Unsicherheit für jedes Verteilungsgesetz streng mathematisch ermittelt werden kann. Dies beseitigt die historisch entwickelte Willkür, die bei der freiwilligen Zuweisung verschiedener Werte der Konfidenzwahrscheinlichkeit unvermeidlich ist. Dies ist besonders wichtig im Bildungsprozess, wenn der Schüler bei der Anwendung der Kalman-Filterung auf eine bestimmte numerische Stichprobe eine Abnahme der Messunsicherheit beobachten kann [13, 14].

Darüber hinaus kann die Kombination der Wahrscheinlichkeits- und Informationseigenschaften der Stichprobe die Art der Verteilung des Zufallsfehlers genauer bestimmen. Dies wird durch eine umfangreiche Datenbank mit numerischen Werten von Parametern wie dem Entropiekoeffizienten und dem Gegenüberschuss für verschiedene Verteilungsgesetze und deren Überlagerung erklärt.

Bewertung der Überlagerung der Verteilungsgesetze einer Zufallsvariablen durch den Entropiekoeffizienten und den Gegenüberschuss (erhalten aus experimentellen Daten)

Wahrscheinlichkeitsverteilungsdichte für jede Spalte des Histogramms [14] breit $$$d$ ist gleich $$$p_ {i} (x_ {i}) = n_ {i} / (n \ cdot d)$ daher ist die Schätzung der Entropiewahrscheinlichkeiten definiert als $$$H \ left (x \ right) = \ int _ {- \ infty} ^ {+ \ infty} p \ left (x \ right) \ ln p \ left (x \ right) dx$ beim Finden der Entropie durch das Histogramm von $$$m$ Spalten erhalten wir das Verhältnis:

$$$\ displaystyle H \ left (x \ right) = - \ sum_ {i = 1} ^ {m} \ int _ {\ tilde {x_ {i}} - \ frac {d} {2}} ^ {\ tilde { x_ {i}} + \ frac {d} {2}} \ frac {n_ {i}} {nd} \ ln \ frac {n_ {i}} {nd} = \ sum_ {i = 1} ^ {m } \ frac {n_ {i}} {n} \ ln \ frac {n} {n_ {i}} + \ ln d$

Wir präsentieren den Ausdruck zur Schätzung der Entropie in folgender Form:

$$$H \ left (x \ right) = \ ln \ left [d \ prod_ {i = 1} ^ {m} \ left (\ frac {n} {n_ {i}} \ right) ^ {\ frac {n_ {i}} {n}} \ right]$

Wir erhalten einen Ausdruck zum Schätzen des Entropiewertes einer Zufallsvariablen:

$$$\ Delta _ {e} = \ frac {1} {2} e ^ {H \ left (x \ right)} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n} \ sum_ {1} ^ {m} n_ {i} \ lg n_ {i}}$

Die Klassifizierung der Verteilungsgesetze erfolgt auf einer Ebene in den Koordinaten des Entropiekoeffizienten $$$k = \ frac {\ Delta _ {e}} {\ sigma}$ und Gegenüberschuss $$$\ psi = \ frac {\ sigma ^ {2}} {\ sqrt {\ mu _ {4}}}$ wo $$$\ mu _ {4} = \ frac {1} {n} \ sum_ {1} ^ {n} \ left (x_ {i} - \ bar {X} \ right) ^ {4}$ .

Für alle möglichen Verteilungsgesetze variiert \ psi von 0 bis 1 und k von 0 bis 2,066, sodass jedes Gesetz durch einen bestimmten Punkt charakterisiert werden kann. Wir zeigen dies mit folgendem Programm:




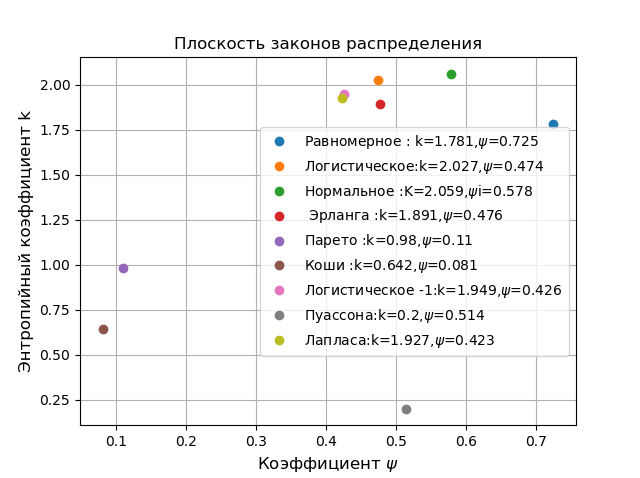
In einer Ebene in Koordinaten $$$k, \ psi$ aus dem Rest der Verteilungen entfernt, die Pareto, Cauchy-Verteilungen, obwohl sie zu verschiedenen Anwendungsgebieten gehören, das erste in der Physik und das zweite in der Wirtschaft. Wählen Sie zum Vergleich die normale Gaußsche Verteilung oben in der Klassifizierung. Alle folgenden Vergleiche werden an einer begrenzten Probe durchgeführt und dienen dazu, die Fähigkeiten eines photonischen Kristalls am Beispiel einer numerischen Bestimmung des Entropiefehlers zu demonstrieren.

Auswahl eines Kalman-Filteralgorithmus

An jedem ausgewählten Punkt im Messbereich werden mehrere Messungen durchgeführt und deren Ergebnis mit einer Messung verglichen, die FC „nicht kennt“. Daher sollten Sie einen FC auswählen, z. B. Kalman-Filter, um eine Konstante zu schätzen [16]. Ich bevorzuge jedoch Python und habe mich für die Option [16] mit umfangreicher Dokumentation entschieden. Ich werde eine Beschreibung des Algorithmus geben:

Da die Konstante immer ein Modell des Systems ist, kann dargestellt werden als:

$$$x_ {k} = x_ {k-1} + w_ {k}$ , (1)

Für das Modell degeneriert die Übergangsmatrix zu Eins und die Kontrollmatrix zu Null. Das Messmodell hat die Form:

$$$y_ {k} = y_ {k-1} + v_ {k}$ , (2)

Für Modell (2) wird die Messmatrix in Einheit und die Kovarianzmatrix konvertiert $$$P, Q, R$ in Dispersionen verwandeln. Am nächsten $$$k$ -th Schritt, bevor die Messergebnisse eintreffen, versucht der Kalman-Skalarfilter, den neuen Zustand des Systems unter Verwendung der Formel (1) zu bewerten:

$$$\ hat {x} _ {k / (k-1)} = \ hat {x} _ {(k-1) / (k-1)}$ , (3)

Gleichung (3) zeigt, dass die A-priori-Schätzung im nächsten Schritt gleich der im vorherigen Schritt vorgenommenen posterioren Schätzung ist. A-priori-Schätzung der Varianz des Fehlers:

$$$P_ {k / (k-1)} = P _ {(k-1) / (k-1)} + Q_ {k}$ , (4)

Nach a priori staatlicher Einschätzung $$$\ hat {x} _ {k / (k-1)}$ Es ist möglich, die Messprognose zu berechnen:

$$$\ hat {y} _ {k} = \ hat {x} _ {k / (k-1)}$ , (5)

Nach der nächsten Messung wird empfangen $$$y_ {k}$ Der Filter berechnet den Fehler seiner Prognose $$$k$ th Messung:

$$$e_ {k} = y_ {k} - \ hat {y} _ {k} = y_ {k} - \ hat {x} _ {k / (k-1)}$ , (6)

Der Filter passt seine Bewertung des Systemzustands an und wählt einen Punkt aus, der irgendwo zwischen der anfänglichen Bewertung liegt $$$\ hat {x} _ {k / (k-1)}$ und der Punkt, der der neuen Dimension entspricht $$$y_ {k}$ ::

$$$e_ {k} = y_ {k} - \ hat {y} _ {k} = y_ {k} - \ hat {x} _ {k / (k-1)}$ , (7)

wo $$$G _ {k}$ - Filterverstärkung.

Die Fehlervarianzschätzung wird ebenfalls korrigiert:

$$$P_ {k / (k)} = (1-G_ {k}) \ cdot P_ {k / (k-1)}$ , (8)

Es kann nachgewiesen werden, dass die Varianz des Fehlers $$$e_ {k}$ ist gleich:

$$$S_ {k} = P_ {k / (k-1)} + R_ {k}$ , (9)

Die Verstärkung des Filters, bei der der minimale Fehler bei der Beurteilung des Systemzustands erreicht wird, wird aus der Beziehung bestimmt

$$$G_ {k} = P_ {k / (k-1)} / S_ {k}$ , (10)

FC-Entropiefehlerminimierung für Rauschen mit Cauchy-, Pareto- und Gauß-Verteilung

1. In der Wahrscheinlichkeitstheorie wird die Cauchy-Verteilungsdichte aus der Beziehung bestimmt:

$$$f (x) = \ frac {b} {\ pi \ cdot (1-x ^ {2})}$

Für diese Verteilung ist es unmöglich, den Fehler mit Methoden der Wahrscheinlichkeitstheorie abzuschätzen ( $$$\ sigma = \ infty$ ), aber die Informationstheorie erlaubt Ihnen dies:




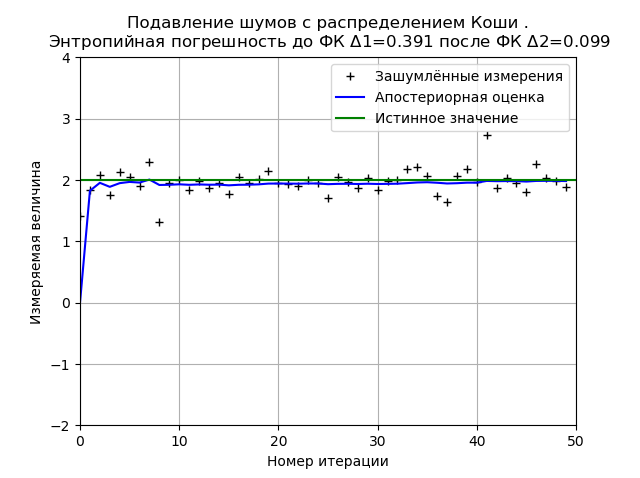
Der Typ des Diagramms kann sich sowohl beim Neustart des Programms (neue Generation der Verteilungsprobe) als auch in Abhängigkeit von der Anzahl der Messungen und Verteilungsparameter ändern, bleibt jedoch unverändert. Der FC minimiert den Wert des Entropiefehlers, der auf der Grundlage der Informationstheorie der Messungen berechnet wird. Für den gegebenen Graphen reduziert FC den Entropiefehler um das 3,9-fache.

2. In der Wahrscheinlichkeitstheorie die Pareto-Verteilungsdichte mit Parametern $$$x_ {m}$ und $$$k$ bestimmt aus dem Verhältnis:

$$

$$f_ {X} (x) = \ left \ {\ begin {matrix} \ frac {kx_ {k} ^ {m}} {x ^ {k + 1}}, & x \ geq x_ {m} \\ 0, & x <x_ {m} \ end {matrix} \ right.$$

Es ist zu beachten, dass die Pareto-Verteilung nicht nur in der Wirtschaft zu finden ist. Sie können das folgende Beispiel für die Verteilung der Dateigröße im Internetverkehr über das TCP-Protokoll geben.

3. In der Wahrscheinlichkeitstheorie die Dichte der Normalverteilung (Gauß) mit mathematischer Erwartung $$$\ mu$ und Standardabweichung $$$\ sigma$ bestimmt aus dem Verhältnis:

$$$f (x) = \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ cdot e ^ {- \ frac {(x- \ mu) ^ {2}} {2 \ sigma ^ {2} }}$

Die Bestimmung der Minimierung des FC-Entropiefehlers aus Rauschen mit einer Gaußschen Verteilung wird zum Vergleich mit nicht-Gaußschen Cauchy- und Pareto-Verteilungen angegeben.




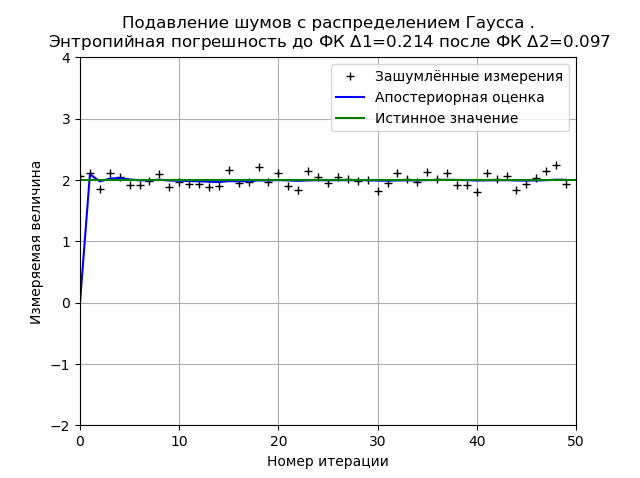
Die Gaußsche Verteilung bietet eine höhere Stabilität des Ergebnisses für 50 Messungen, und für das gezeigte Diagramm nimmt der Entropiefehler um das 2,2-fache ab.

Minimierung des FC-Entropiefehlers aus einer Stichprobe experimenteller Daten mit einem unbekannten Rauschverteilungsgesetz




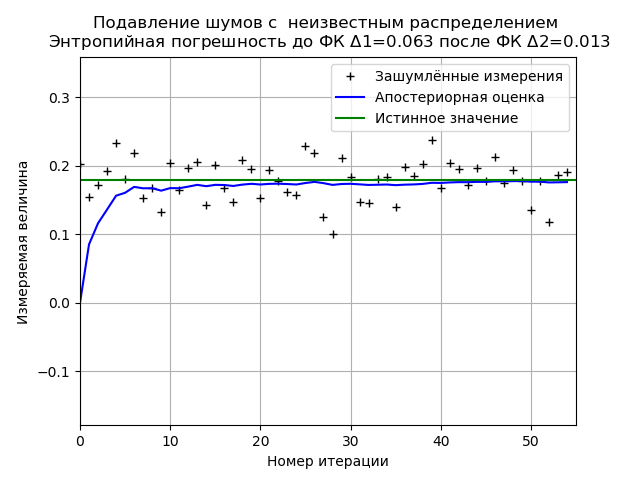
Bei der Analyse einer Stichprobe experimenteller Daten erhalten wir stabile Ergebnisse zur Minimierung des FC-Entropiefehlers. Für dieses Beispiel reduziert der FC den Entropiefehler um das 4,85-fache.

Fazit

Alle Vergleiche in diesem Artikel wurden an begrenzten Datenstichproben durchgeführt. Daher sollten grundlegende Schlussfolgerungen unterlassen werden. Die Verwendung von Entropiefehlern ermöglicht es uns jedoch, die Wirksamkeit des Kalman-Filters in der gegebenen Implementierung zu quantifizieren. Daher kann die Trainingsaufgabe dieses Artikels als abgeschlossen betrachtet werden.