Einschätzung der räumlichen Ausrichtung oder Wie man keine Angst vor Mahoney- und Majwik-Filtern hat

Worüber reden wir?

Das Erscheinen eines Beitrags über den Majwik-Filter auf Habre war auf seine Weise ein symbolisches Ereignis. Offensichtlich hat die allgemeine Begeisterung für Drohnen das Interesse an der Aufgabe wiederbelebt, die Orientierung des Körpers durch Trägheitsmessungen zu beurteilen. Gleichzeitig befriedigten traditionelle Methoden, die auf dem Kalman-Filter basierten, die Öffentlichkeit nicht mehr - entweder aufgrund der hohen Anforderungen an Rechenressourcen, die für Drohnen nicht akzeptabel waren, oder aufgrund der komplexen und nicht intuitiven Einstellungen.

Der Beitrag wurde von einer sehr kompakten und effizienten Implementierung des Filters für C begleitet. Den Kommentaren nach zu urteilen, blieb die physikalische Bedeutung dieses Codes sowie des gesamten Artikels für einige jedoch vage. Nun, wir geben ehrlich zu: Der Majwik-Filter ist der komplizierteste der Filtergruppe, der im Allgemeinen auf sehr einfachen und eleganten Prinzipien basiert. Ich werde diese Grundsätze in meinem Beitrag berücksichtigen. Der Code wird nicht hier sein. Mein Beitrag handelt nicht von einer bestimmten Implementierung des Orientierungsschätzungsalgorithmus, sondern von einer Einladung, eigene Variationen zu einem bestimmten Thema zu erfinden, was sehr viel sein kann.

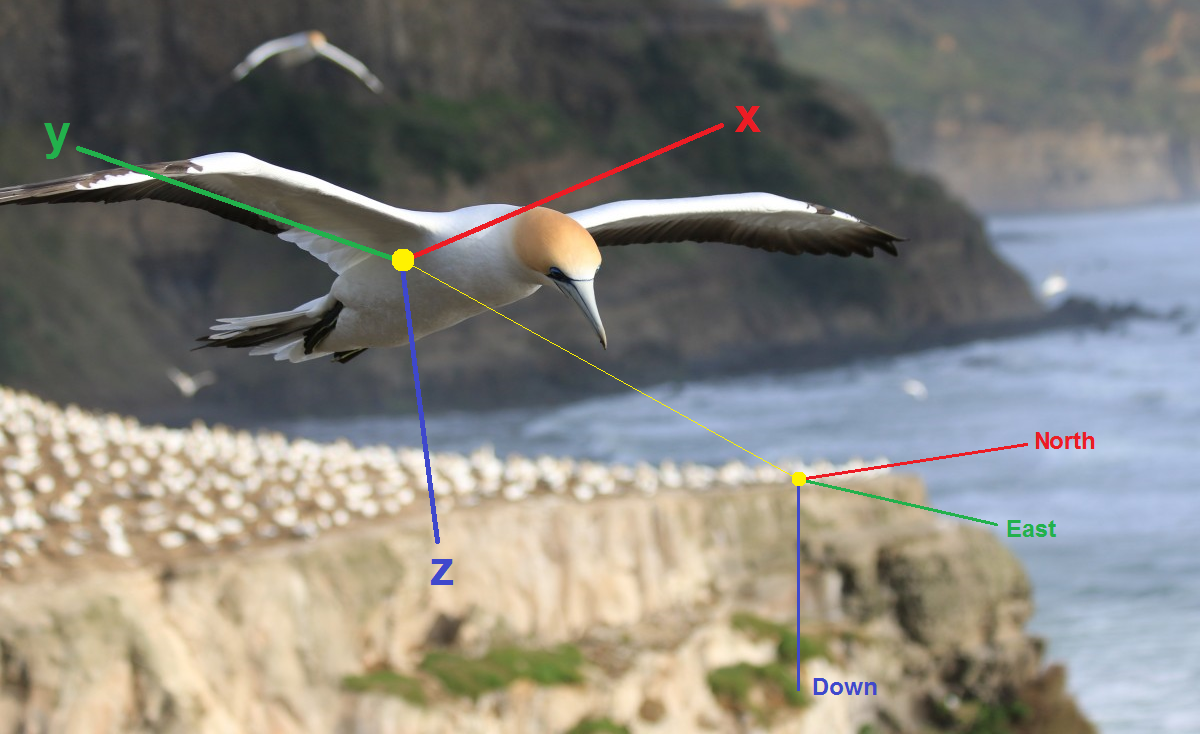
Orientierungsansicht

Erinnern Sie sich an die Grundlagen. Um die Ausrichtung des Körpers im Raum zu beurteilen, müssen Sie zuerst einige Parameter auswählen, die zusammen diese Ausrichtung eindeutig bestimmen, d. H. im wesentlichen die Ausrichtung des zugehörigen Koordinatensystems $$$xyz$ relativ bedingt festes System - zum Beispiel das geografische System NED (Nord, Ost, Unten). Dann müssen Sie kinematische Gleichungen erstellen, d. H. Drücken Sie die Änderungsrate dieser Parameter durch die Winkelgeschwindigkeit der Gyroskope aus. Schließlich müssen Vektormessungen von Beschleunigungsmessern, Magnetometern usw. in die Berechnung einbezogen werden. Hier sind die gebräuchlichsten Arten, Orientierung darzustellen:

Eulerwinkel - rollen (rollen, $$$\ phi$ ), Tonhöhe (Tonhöhe, $$$\ theta$ ), Kurs (Überschrift, $$$\ psi$ ) Dies ist der intuitivste und prägnanteste Satz von Orientierungsparametern: Die Anzahl der Parameter entspricht genau der Anzahl der Rotationsfreiheitsgrade. Für diese Winkel können wir die kinematischen Gleichungen von Euler schreiben. Sie mögen die theoretische Mechanik sehr gern, aber bei Navigationsproblemen sind sie wenig nützlich. Erstens erlaubt die Kenntnis der Winkel nicht die direkte Konvertierung der Komponenten eines Vektors von einem mit einem geografischen Koordinatensystem verbundenen oder umgekehrt. Zweitens degenerieren bei einer Neigung von ± 90 Grad die kinematischen Gleichungen, die Rolle und der Kurs werden unbestimmt.

Rotationsmatrix - Matrix $$$\ mathbf {C}$ 3 × 3-Größe, mit der Sie einen beliebigen Vektor im zugehörigen Koordinatensystem multiplizieren müssen, um denselben Vektor im geografischen System zu erhalten: $$$\ mathbf {r} _ {NED} = \ mathbf {C} \ mathbf {r} _ {xyz}$ . Die Matrix ist immer orthogonal, d.h. $$$\ mathbf {C} = \ mathbf {C} ^ {T}$ . Die kinematische Gleichung dafür hat die Form $$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega}$ .
Hier $$$\ mathbf {\ Omega}$ - eine Matrix von Winkelgeschwindigkeitskomponenten, die mit Gyroskopen in einem verbundenen Koordinatensystem gemessen werden:

$$

$$\ mathbf {\ Omega} = \ begin {bmatrix} 0 & - \ omega_ {z} & \ omega_ {y} \\ \ omega_ {z} & 0 & - \ omega_ {x} \\ - \ omega_ {y } & \ omega_ {x} & 0 \\ \ end {bmatrix}$$

Die Rotationsmatrix ist etwas weniger offensichtlich als die Euler-Winkel, aber im Gegensatz zu ihnen können Sie Vektoren direkt konvertieren und verlieren an keiner Winkelposition an Bedeutung. Aus rechnerischer Sicht ist der Hauptnachteil die Redundanz: Aus Gründen von drei Freiheitsgraden werden neun Parameter gleichzeitig eingeführt, und alle müssen gemäß der kinematischen Gleichung aktualisiert werden. Das Problem kann durch Verwendung der Orthogonalität der Matrix leicht vereinfacht werden.

Die Quaternion der Rotation ist ein radikales, aber sehr unintuitives Mittel gegen Redundanz und Degeneration. Dies ist ein Vier-Komponenten-Objekt. $$$\ mathbf {q} = q_ {0} + q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ - keine Zahl, kein Vektor und keine Matrix. Das Quaternion kann aus zwei Winkeln betrachtet werden. Wie wäre es zunächst mit der formalen Menge des Skalars? $$$q_ {0}$ und Vektor $$$q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ wo $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ - Einheitsachsenvektoren (was natürlich absurd klingt). Zweitens als Verallgemeinerung komplexer Zahlen, wo wir jetzt nicht eine, sondern drei verschiedene imaginäre Einheiten verwenden $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ (was nicht weniger absurd klingt). Wie hängt eine Quaternion mit einer Wende zusammen? Durch Eulers Theorem: Ein Körper kann immer mit einer endlichen Drehung in einem bestimmten Winkel von einer bestimmten Orientierung zur anderen übertragen werden $$$\ alpha$ um eine Achse mit einem Führungsvektor $$$\ mathbf {u}$ . Diese Winkel und Achsen können zu einer Quaternion kombiniert werden: $$$\ mathbf {q} = \ mathrm {cos} (\ alpha / 2) + \ mathbf {u} \ mathrm {sin} (\ alpha / 2)$ . Wie eine Matrix kann eine Quaternion verwendet werden, um einen beliebigen Vektor direkt von einem Koordinatensystem in ein anderes umzuwandeln: $$$\ mathbf {r} _ {NED} = \ mathbf {q} \ mathbf {r} _ {xyz} {\ mathbf {q}} ^ {- 1}$ . Wie Sie sehen können, leidet auch die Quaternionendarstellung der Orientierung unter Redundanz, jedoch viel weniger als die Matrix: Ein zusätzlicher Parameter ist nur einer. Die umfassende Überprüfung der Quaternionen erfolgte bereits bei Habré . Sie sprachen über Geometrie und 3D-Grafiken. Wir interessieren uns auch für die Kinematik, da die Änderungsrate des Quaternions mit der gemessenen Winkelgeschwindigkeit in Beziehung gesetzt werden muss. Die entsprechende kinematische Gleichung hat die Form $$$\ dot {\ mathbf {q}} = 1/2 \ mathbf {q} \ mathbf {\ omega}$ Wo ist der Vektor? $$$\ mathbf {\ omega}$ wird auch als Quaternion mit einem skalaren Teil von Null betrachtet.

Filterschemata

Der naivste Ansatz zur Berechnung der Orientierung besteht darin, sich mit einer kinematischen Gleichung zu bewaffnen und einen beliebigen Satz von Parametern entsprechend zu aktualisieren. Wenn wir zum Beispiel eine Rotationsmatrix wählen, können wir einen Zyklus mit etwas im Sinne von C += * Omega * dt schreiben. Das Ergebnis wird enttäuschen. Gyroskope, insbesondere MEMS, weisen große und instabile Nullpunktverschiebungen auf. Infolgedessen weist die berechnete Ausrichtung selbst in völliger Ruhe einen unbegrenzten Akkumulationsfehler (Drift) auf. Alle von Mahoney, Majwick und vielen anderen erfundenen Tricks, die mich nicht ausschließen, zielten darauf ab, diese Abweichung durch Messungen von Beschleunigungsmessern, Magnetometern, GNSS-Empfängern, Verzögerungen usw. zu kompensieren. So entstand eine ganze Familie von Orientierungsfiltern, die auf einem einfachen Grundprinzip basieren.

Grundprinzip. Um die Orientierungsdrift zu kompensieren, muss der von Gyroskopen gemessenen Winkelgeschwindigkeit eine zusätzliche Steuerwinkelgeschwindigkeit hinzugefügt werden, die auf der Grundlage von Vektormessungen anderer Sensoren konstruiert wurde. Der Kontrollwinkelgeschwindigkeitsvektor sollte sich bemühen, die Richtungen der gemessenen Vektoren mit ihren bekannten wahren Richtungen zu kombinieren.

Hier wird ein völlig anderer Ansatz gewählt als bei der Konstruktion des Korrekturterms des Kalman-Filters. Der Hauptunterschied besteht darin, dass die Steuerwinkelgeschwindigkeit kein Term ist, sondern ein Faktor für den geschätzten Wert (Matrix oder Quaternion). Daraus ergeben sich wichtige Vorteile:

• Ein Auswertungsfilter kann für die Ausrichtung selbst erstellt werden und nicht für kleine Abweichungen der Ausrichtung von der von den Gyroskopen bereitgestellten. Darüber hinaus erfüllen die geschätzten Werte automatisch alle Anforderungen, die die Aufgabe stellt: Die Matrix ist orthogonal, die Quaternion normalisiert.
• Die physikalische Bedeutung der Steuerwinkelgeschwindigkeit ist viel klarer als der Korrekturterm im Kalman-Filter. Alle Manipulationen werden mit Vektoren und Matrizen im gewöhnlichen dreidimensionalen physikalischen Raum und nicht in einem abstrakten mehrdimensionalen Zustandsraum durchgeführt. Dies vereinfacht die Verfeinerung und Anpassung des Filters erheblich und ermöglicht es Ihnen als Bonus, großdimensionale Matrizen und schwere Matrixbibliotheken zu entfernen.

Lassen Sie uns nun sehen, wie diese Idee in bestimmten Filteroptionen implementiert wird.

Mahoney Filter. Die ganze wütende Mathematik des ursprünglichen Mahoney-Artikels wurde geschrieben, um einfache Gleichungen zu rechtfertigen (32). Wir schreiben sie in unserer Notation um. Wenn wir die Schätzung der Nullpunktverschiebungen der Gyroskope ignorieren, bleiben zwei Schlüsselgleichungen übrig - die kinematische Gleichung für die Rotationsmatrix selbst (mit der Steuerwinkelgeschwindigkeit in Form einer Matrix $$$\ mathbf {\ Omega} '$ ) und das Gesetz der Bildung dieser Geschwindigkeit in Form eines Vektors $$$\ mathbf {\ omega} '$ . Der Einfachheit halber nehmen wir an, dass es keine Beschleunigungen oder magnetischen Aufnehmer gibt, und dank dessen stehen uns Beschleunigungsmessungen im freien Fall zur Verfügung. $$$- \ hat {\ mathbf {g}} _ {xyz}$ von Beschleunigungsmessern und dem Magnetfeld der Erde $$$\ hat {\ mathbf {m}} _ {xyz}$ von Magnetometern. Beide Vektoren werden von Sensoren in einem verbundenen Koordinatensystem gemessen, und im geografischen System ist ihre Position bekannt: $$$- \ mathbf {g} _ {NED}$ nach oben zeigen $$$\ mathbf {m} _ {NED}$ - nach magnetischem Norden. Dann sehen die Mahoney-Filtergleichungen folgendermaßen aus:

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} (\ mathbf {\ Omega} + \ mathbf {\ Omega} ') \\ \ mathbf {\ omega'} = k_ {g} \ hat {\ mathbf {g}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {g} _ {NED} + k_ {m} \ hat {\ mathbf {m}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {m} _ {NED}$$

Schauen wir uns die zweite Gleichung genau an. Der erste Term auf der rechten Seite ist ein Vektorprodukt. Der erste Faktor ist die gemessene Erdbeschleunigung, der zweite ist wahr. Da sich die Faktoren in einem Koordinatensystem befinden müssen, wird der zweite Faktor durch Multiplikation mit in ein verbundenes System umgewandelt $$$\ mathbf {C} ^ {T}$ . Die als Vektorprodukt konstruierte Winkelgeschwindigkeit ist senkrecht zur Ebene der Faktorvektoren. Sie können die geschätzte Position des zugehörigen Koordinatensystems drehen, bis die Faktorvektoren in Richtung übereinstimmen. Dann wird das Vektorprodukt auf Null zurückgesetzt und die Drehung stoppt. Koeffizient $$$k_ {g}$ legt die Starrheit eines solchen Feedbacks fest. Der zweite Term führt eine ähnliche Operation mit einem Magnetvektor durch. Tatsächlich verkörpert der Mahoney-Filter die bekannte These: Die Kenntnis von zwei nichtkollinearen Vektoren in zwei verschiedenen Koordinatensystemen ermöglicht es Ihnen, die gegenseitige Ausrichtung dieser Systeme eindeutig wiederherzustellen. Wenn mehr als zwei Vektoren vorhanden sind, bietet dies eine nützliche Messredundanz. Wenn es nur einen Vektor gibt, kann ein Rotationsfreiheitsgrad (Bewegung um diesen Vektor) nicht festgelegt werden. Zum Beispiel, wenn nur ein Vektor angegeben ist $$$- \ mathbf {g}$ Dann können Sie die Drift von Roll und Pitch einstellen, aber nicht den Kurs.

Natürlich muss der Mahoney-Filter keine Rotationsmatrix verwenden. Es gibt auch nichtkanonische Quaternionsvarianten.

Virtuelle Kreiselplattform. Im Mahoney-Filter haben wir die Steuerwinkelgeschwindigkeit angewendet $$$\ mathbf {\ omega '}$ zum zugehörigen Koordinatensystem. Sie können es jedoch auf die geschätzte Position des geografischen Koordinatensystems anwenden. Die kinematische Gleichung nimmt dann die Form an

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega} - \ mathbf {\ Omega} '\ mathbf {C}$$

Es stellt sich heraus, dass dieser Ansatz den Weg für sehr fruchtbare physikalische Analogien ebnet. Es genügt, sich daran zu erinnern, womit die Kreiseltechnik begann - die vertikalen und trägen Navigationssysteme, die auf der gyrostabilisierten Plattform in einem Kardanrahmen basieren.


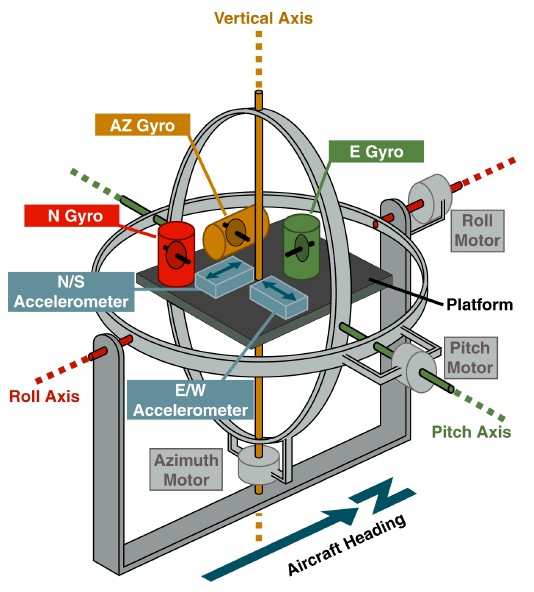www.theairlinepilots.com

Das Ziel der dortigen Plattform war die Materialisierung des geografischen Koordinatensystems. Die Ausrichtung des Trägers wurde relativ zu dieser Plattform durch Winkelsensoren an den Aufhängungsrahmen gemessen. Wenn die Gyroskope eine Drift hatten, driftete auch die Plattform hinter ihnen her, und Fehler wurden in den Messwerten der Winkelsensoren akkumuliert. Um diese Fehler zu beseitigen, wurde eine Rückmeldung von auf der Plattform installierten Beschleunigungsmessern eingeführt. Beispielsweise wurde die Abweichung der Plattform vom Horizont um die Nordachse vom Beschleunigungsmesser der Ostachse wahrgenommen. Dieses Signal ermöglichte das Einstellen der Steuerwinkelgeschwindigkeit $$$\ mathbf {\ omega '}$ Rückkehr der Plattform zum Horizont.

Wir können die gleichen visuellen Konzepte in unserer Aufgabe verwenden. Die beschriebene kinematische Gleichung muss dann wie folgt gelesen werden: Die Änderungsrate der Orientierung ist die Differenz zwischen zwei Rotationsbewegungen - der absoluten Bewegung des Trägers (erster Term) und der absoluten Bewegung der virtuellen Kreiselplattform (zweiter Term). Die Analogie kann auf das Gesetz der Bildung der steuernden Winkelgeschwindigkeit erweitert werden. Vektor $$$- \ hat {\ mathbf {g}} _ {NED} = - \ mathbf {C} \ hat {\ mathbf {g}} _ {xyz}$ Es ist das Zeugnis von Beschleunigungsmessern, die angeblich auf einer Kreiselplattform stehen. Dann können Sie aus physischen Gründen schreiben:

$$

$$\ omega '_ {N} = - gk_ {g} \ hat {g} _ {E}, \; \ omega '_ {E} = gk_ {g} \ hat {g} _ {N}$$

Es wäre möglich, auf formale Weise zu genau demselben Ergebnis zu gelangen, indem die Vektormultiplikation im Geiste des Mahoney-Filters durchgeführt wird, jetzt jedoch nicht in einem zusammenhängenden, sondern in einem geografischen Koordinatensystem. Ist es nur notwendig?

Der erste Hinweis auf eine nützliche Analogie zwischen Plattform- und Strapdown-Trägheitsnavigation erscheint offenbar im alten Boeing-Patent . Dann wurde diese Idee von Salychev und kürzlich - auch von mir - aktiv entwickelt. Die offensichtlichen Vorteile dieses Ansatzes:

• Die Steuerwinkelgeschwindigkeit kann auf der Grundlage verständlicher physikalischer Prinzipien gebildet werden.
• Natürlich sind die horizontalen und gerichteten Kanäle, die sich in ihren Eigenschaften und Korrekturmethoden stark unterscheiden, getrennt. Im Mahoney-Filter werden sie gemischt.
• Es ist zweckmäßig, den Effekt von Beschleunigungen aufgrund der Verwendung von GNSS-Daten zu kompensieren, die genau in geografischen und nicht in verwandten Achsen ausgegeben werden.
• Es ist einfach, den Algorithmus auf den Fall einer hochpräzisen Trägheitsnavigation zu verallgemeinern, bei der die Form und Rotation der Erde berücksichtigt werden muss. Wie das im Mahoney-Schema geht, kann ich mir nicht vorstellen.

Majwick Filter. Majwik entschied sich für den harten Weg . Wenn Mahoney anscheinend intuitiv zu seiner Entscheidung kam und sie dann mathematisch begründete, dann erwies sich Majwik von Anfang an als Formalist. Er verpflichtete sich, das Optimierungsproblem zu lösen. Er überlegte so. Stellen Sie die Ausrichtung des Rotationsquaternions ein. Im Idealfall die berechnete Richtung eines gemessenen Vektors (lassen Sie uns dies haben $$$- \ mathbf {g}$ ) fällt mit dem wahren zusammen. Dann wird es sein $$${\ mathbf {q}} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q} = \ hat {\ mathbf {g}} _ {xyz}$ . In der Realität ist dies nicht immer erreichbar (insbesondere wenn mehr als zwei Vektoren vorhanden sind), aber Sie können versuchen, die Abweichung zu minimieren $$$\ mathbf {F} = {\ mathbf {q} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q}} - \ hat {\ mathbf {g}} _ {xyz}$ von der exakten Gleichheit. Dazu führen wir das Minimierungskriterium ein

$$

$$E = \ frac {1} {2} | \ mathbf {F} | ^ {2} \ rightarrow \ mathrm {min}$$

Die Minimierung erfordert einen Gradientenabstieg, der sich in kleinen Schritten in die dem Gradienten entgegengesetzte Richtung bewegt $$$\ nabla E$ d.h. im Gegensatz zu der schnellsten Funktionssteigerung $$$E$ . Majwik macht übrigens einen Fehler: In all seinen Werken stellt er nicht vor $$$E$ und schreibt beharrlich $$$\ nabla \ mathbf {F}$ statt $$$\ nabla E$ , obwohl es tatsächlich genau berechnet $$$\ nabla E$ .

Infolgedessen führt der Gradientenabstieg zu der folgenden Bedingung: Um die Orientierungsdrift zu kompensieren, muss aus der kinematischen Gleichung ein neuer negativer Term proportional zur kinematischen Gleichung hinzugefügt werden $$$\ nabla E$ ::

$$

$$\ dot {\ mathbf {q}} = \ frac {1} {2} \ mathbf {q} \ mathbf {\ omega} - \ beta \ frac {\ nabla E} {| \ nabla E |}$$

Hier weicht Majwik ein wenig von unserem „Grundprinzip“ ab: Er addiert den Korrekturterm nicht zur Winkelgeschwindigkeit, sondern zur Änderungsrate der Quaternion, und das ist nicht genau dasselbe. Infolgedessen kann sich herausstellen, dass die aktualisierte Quaternion nicht mehr einzeln ist und dementsprechend die Fähigkeit verliert, die Orientierung darzustellen. Daher ist für den Majwik-Filter eine künstliche Normalisierung des Quaternions eine wichtige Operation, während sie für andere Filter wünschenswert und nicht optional ist.

Der Effekt der Beschleunigung

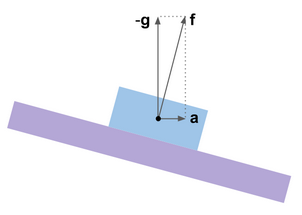
Bisher wurde angenommen, dass es keine echten Beschleunigungen gibt und Beschleunigungsmesser nur die Gravitationsbeschleunigung messen $$$- \ mathbf {g}$ . Dies ermöglichte es, einen vertikalen Standard zu erhalten und mit seiner Hilfe Roll- und Nickdrift zu kompensieren. Im allgemeinen Fall messen Beschleunigungsmesser jedoch unabhängig von ihrem Funktionsprinzip die scheinbare Beschleunigung - die Vektordifferenz der tatsächlichen Beschleunigung und der Gravitationsbeschleunigung $$$\ mathbf {f} = \ mathbf {a} - \ mathbf {g}$ . Die Richtung der scheinbaren Beschleunigung stimmt nicht mit der Vertikalen überein, und Fehler, die durch Beschleunigungen verursacht werden, erscheinen in den Roll- und Nickschätzungen.

Dies lässt sich anhand der Analogie einer virtuellen Kreiselplattform leicht veranschaulichen. Ihr Korrektursystem ist so ausgelegt, dass die Plattform in der Winkelposition stoppt, in der die Signale der angeblich darauf installierten Beschleunigungsmesser auf Null zurückgesetzt werden, d. H. wenn der gemessene Vektor $$$\ mathbf {f}$ wird senkrecht zu den Achsen der Empfindlichkeit der Beschleunigungsmesser. Wenn es keine Beschleunigung gibt, fällt diese Position mit dem Horizont zusammen. Wenn horizontale Beschleunigungen auftreten, wird die Kreiselplattform ausgelenkt. Wir können sagen, dass die Kreiselplattform einem stark gedämpften Pendel oder Lot ähnelt.



In den Kommentaren zum Beitrag über den Majwik-Filter stellte sich die Frage, ob man hoffen kann, dass dieser Filter weniger anfällig für Beschleunigungen ist als beispielsweise der Mahoney-Filter. Leider nutzen alle hier beschriebenen Filter dieselben physikalischen Prinzipien und leiden daher unter denselben Problemen. Es ist unmöglich, die Physik mit der Mathematik zu täuschen. Was ist dann zu tun?

Der einfachste und härteste Weg wurde bereits Mitte des letzten Jahrhunderts für Kreisel in der Luftfahrt erfunden: die Kontrollwinkelgeschwindigkeit bei Vorhandensein von Beschleunigungen oder die Winkelgeschwindigkeit des Kurses (die den Eintritt in eine Kurve anzeigt) zu reduzieren oder vollständig auf Null zu setzen. Die gleiche Methode kann auf aktuelle Plattformsysteme angewendet werden. In diesem Fall müssen Beschleunigungen anhand der Werte beurteilt werden $$$\ hat {f} _ {N}, \ hat {f} _ {E}$ , und nicht $$$\ hat {f} _ {x}, \ hat {f} _ {y}$ die wiederum selbst Null sind. Jedoch in der Größe $$$\ hat {\ mathbf {f}} _ {NED}$ Es ist nicht immer möglich, echte Beschleunigungen von Projektionen der Gravitationsbeschleunigung zu unterscheiden, die auf die Neigung der Kreiselplattform zurückzuführen sind, die beseitigt werden muss. Daher funktioniert die Methode nicht zuverlässig - es sind jedoch keine zusätzlichen Sensoren erforderlich.

Eine genauere Methode basiert auf der Verwendung externer Geschwindigkeitsmessungen vom GNSS-Empfänger. Wenn Geschwindigkeit bekannt ist $$$\ mathbf {v}$ , dann kann es numerisch differenziert werden und echte Beschleunigung erhalten $$$\ dot {\ mathbf {v}}$ . Dann der Unterschied $$$\ hat {\ mathbf {f}} _ {NED} - \ dot {\ mathbf {v}}$ wird genau gleich sein $$$- \ hat {\ mathbf {g}} _ {NED}$ unabhängig von der Medienbewegung. Es kann als vertikaler Standard verwendet werden. Beispielsweise können Sie die Steuerwinkelgeschwindigkeit der Kreiselplattform im Formular angeben

$$

$$\ omega '_ {N} = gk_ {g} (\ hat {f} _ {E} - \ dot {v} _ {E}), \; \ omega '_ {E} = - gk_ {g} (\ hat {f} _ {N} - \ dot {v} _ {N})$$

Sensor-Nullpunkt-Offsets

Ein trauriges Merkmal von Gyroskopen und Beschleunigungsmessern für Verbraucher ist die große Instabilität von Zeit- und Temperaturversätzen von Null. Um sie zu beseitigen, reicht eine Kalibrierung im Werk oder im Labor nicht aus - Sie müssen sie während des Betriebs neu bewerten.

Gyroskope. Wir werden uns mit Null-Offsets von Gyroskopen befassen $$$\ delta {\ mathbf {\ omega}}$ . Die geschätzte Position des zugehörigen Koordinatensystems entfernt sich von seiner tatsächlichen Position mit einer Winkelgeschwindigkeit, die durch zwei entgegengesetzte Faktoren bestimmt wird - Nullverschiebungen der Gyroskope und Steuerung der Winkelgeschwindigkeit: $$$\ delta {\ mathbf {\ omega}} - \ mathbf {\ omega '}$ . Wenn es dem Korrektursystem (z. B. im Mahoney-Filter) gelungen ist, den Ausgang zu stoppen, ist dies im eingeschwungenen Zustand der Fall $$$\ delta {\ mathbf {\ omega}} = \ mathbf {\ omega '}$ . Mit anderen Worten, bei der Steuerung Winkelgeschwindigkeit $$$\ mathbf {\ omega '}$ Informationen über eine unbekannte gültige Störung $$$\ delta {\ mathbf {\ omega}}$ . Daher kann eine kompensatorische Schätzung angewendet werden: Wir kennen die Größe der Störung nicht direkt, wissen jedoch, welche Korrekturmaßnahmen erforderlich sind, um sie auszugleichen. Dies ist die Grundlage für die Schätzung der Nullpunktverschiebungen von Gyroskopen. In Mahoney wird beispielsweise die Punktzahl gemäß dem Gesetz aktualisiert

$$

$$\ dot {\ hat {\ delta \ mathbf {\ omega}}} = k_ {b} \ mathbf {\ omega '}$$

Das Ergebnis ist jedoch seltsam: Schätzungen erreichen 0,04 rad / s. Eine solche Instabilität von Null-Offsets tritt selbst bei den schlimmsten Gyroskopen nicht auf. Ich vermute, das Problem ist, dass Mahoney kein GNSS oder andere externe Sensoren verwendet - und vollständig vom Einfluss von Beschleunigungen betroffen ist. Nur auf der vertikalen Achse, wo die Beschleunigung keinen Schaden anrichtet, sieht die Schätzung mehr oder weniger robust aus:


Mahony et al., 2008

Beschleunigungsmesser Rate Zero Offset Beschleunigungsmesser $$$\ delta {\ mathbf {f}}$ viel schwieriger. Informationen über sie müssen aus derselben Steuerwinkelgeschwindigkeit extrahiert werden $$$\ mathbf {\ omega '}$ . Bei einer geradlinigen Bewegung ist der Effekt der Nullpunktverschiebung der Beschleunigungsmesser jedoch nicht von der Neigung des Trägers oder der Neigung der Installation des Sensorblocks darauf zu unterscheiden. 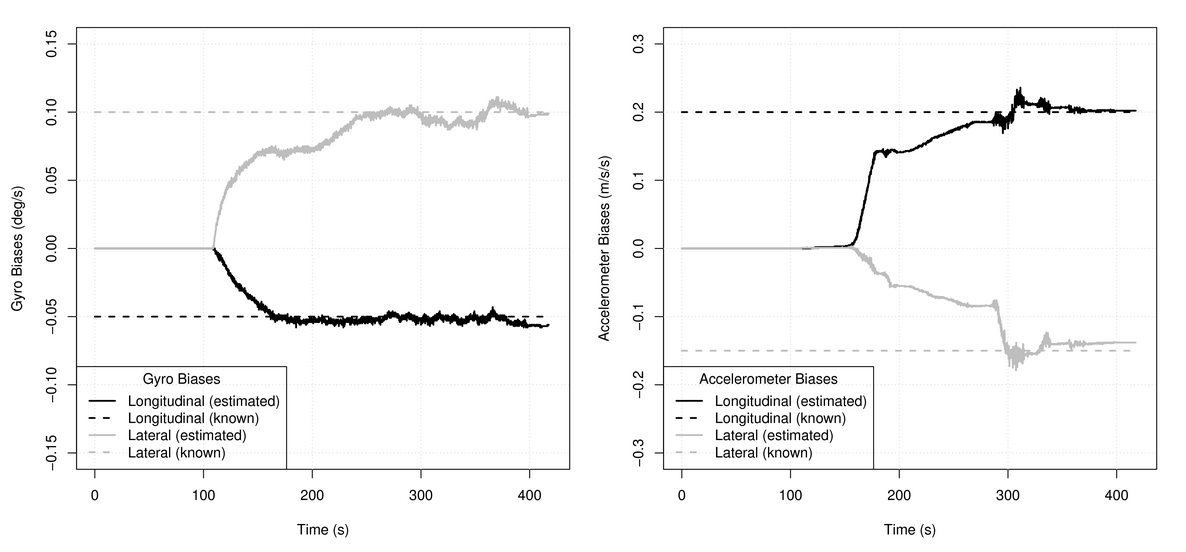Keine Zusätze zu $$$\ mathbf {\ omega '}$ Beschleunigungsmesser erstellen nicht. Das Additiv erscheint nur in einer Umdrehung, wodurch wir die Fehler von Gyroskopen und Beschleunigungsmessern trennen und unabhängig bewerten können. Ein Beispiel dafür ist in meinem Artikel . Hier sind die Bilder von dort:

Anstelle einer Schlussfolgerung: Was ist mit dem Kalman-Filter?

Ich habe keinen Zweifel daran, dass die hier beschriebenen Filter in Bezug auf Geschwindigkeit, Kompaktheit des Codes und einfache Einrichtung fast immer einen Vorteil gegenüber dem herkömmlichen Kalman-Filter haben - dafür wurden sie erstellt. In Bezug auf die Genauigkeit der Bewertung ist hier nicht alles so klar. Ich traf erfolglos entworfene Kalman-Filter, die in ihrer Genauigkeit einem Filter mit einer virtuellen Kreiselplattform deutlich unterlegen waren. Majwik hat auch die Vorteile seines Filters in Bezug auf einige Kalman-Schätzungen bewiesen. Für dieselbe Orientierungsschätzungsaufgabe können Sie jedoch mindestens ein Dutzend verschiedene Kalman-Filterschaltungen erstellen, von denen jede über unzählige Einstellungen verfügt. Ich habe keinen Grund zu der Annahme, dass der Mahoney- oder Majwik-Filter genauer ist als der bestmögliche Kalman-Filter. Und natürlich hat der Kalman-Ansatz immer den Vorteil der Universalität: Er legt keine strengen Einschränkungen für die spezifischen dynamischen Eigenschaften des bewerteten Systems fest.