Teil 2. Sehr schwerer Kraftstoff
Vorheriger Teil 1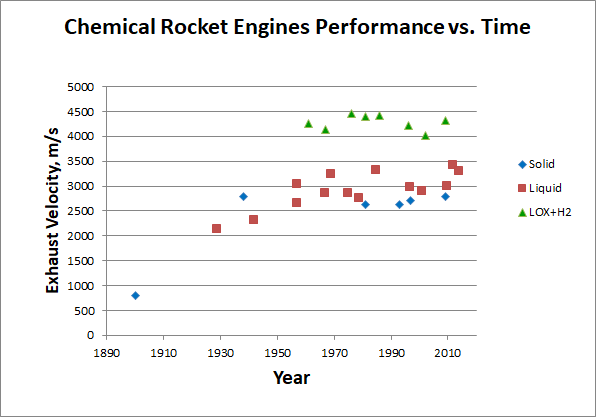
Vor Ihnen liegt die Internationale Raumstation. Mit einer Masse von 420 Tonnen und einem Wert von
[ 20 ] von 150 Milliarden US-Dollar:

Ihre kinetische Energie, das gute alte
E =
mv 2/2 , beträgt 1,3 * 10
13 Joule. Wenn wir potenzielle Energie in einer Höhe von 400 Kilometern hinzufügen, erhalten wir 1,4 * 10
13 J.
Wie viel Gas müssen Sie verbrennen, um diese Energie zu erhalten? Es stellt sich heraus, dass nicht so sehr. Insgesamt 350 Tonnen. Dies ist ungefähr das
[ 200 ] eintägige Energiebudget von Ulan-Ude.
Wie kommt es, dass weit entfernt von der reichsten Stadt der Welt an einem einzigen Tag genug Energie zur Verfügung steht, um die ISS auf Umlaufgeschwindigkeit zu beschleunigen? Wir haben jedoch eine Station für die ganze Welt und es kostet unanständig verrücktes Geld?
Die Antwort
liegt im Offensichtlichen aus der Anatomie der Trägerrakete.
Der Beförderer muss mindestens Folgendes umfassen:
- Nutzlast. Warum wird es sonst überhaupt benötigt?
- Mindestens ein Motor.
- Ein Gehäuse, das all dies verbindet.
- Und natürlich Kraftstoff. Als Arbeitsmedium und in den meisten Fällen als Energiequelle.
Und im letzten Absatz ist das Problem verwurzelt. Um ein bestimmtes Minimum an Kraftstoff anzuheben und zu ziehen, benötigen Sie ... richtig, zusätzlichen Kraftstoff! Auf dem Vormarsch brauchen Sie auch Kraftstoff! Und diese Verpackung hält lange an. Natürlich konvergiert es, sonst würden wir nirgendwo fliegen. Aber nach den Ergebnissen der Konvergenz besteht eine moderne Rakete, selbst eine mehrstufige, sogar qualitativ hochwertige Rakete, die hauptsächlich aus Masse besteht, hauptsächlich aus diesem Treibstoff.
Nun, hier ist ein Lehrbuchbeispiel: Saturn V ist nicht die neueste, sondern eine der effektivsten Raketen in der Geschichte
[ 30 ] :

[Originalbild aus der NASA-Geschichte [
40 ]]
Startgewicht - 2970 Tonnen. Etwa 2670 davon sind Treibstoff. Davon brennen 2160 in weniger als drei Minuten der gesamten Mondexpedition aus. Trotz der Tatsache, dass die kinetische Energie der Nutzlast im Orbit nur 100 Tonnen Kraftstoff „kostet“.
Es stellt sich heraus, dass die Hauptschwierigkeit beim Eintritt in die Umlaufbahn nicht ein Energiemangel ist. Ihre Erdbewohner haben nicht nur für die Stationen, sondern auch für Kreuzfahrtschiffe im Orbit reichlich kinetische Energie. Das Problem ist anders: Unser Kraftstoff ist zu schwer. In Kilogramm wird zu viel davon benötigt, um die für den Flug erforderliche Energiemenge zu sammeln. Warum
sollte der größte Teil des in die Rakete eingefüllten Treibstoffs für den Transport von Treibstoff verwendet werden? Tatsächlich sagt uns die Tsiolkovsky-Formel, die das Start-
M und die Endmasse der Rakete
m mit der Geschwindigkeit
V und der Abgasgeschwindigkeit des Motors
u verbindet , dasselbe:
M /
m = e
V / u [2]
Auf den ersten Blick ist nicht ganz klar, was der Energiegehalt pro Kilogramm damit zu tun hat. Aber alles ist einfach. Es "sitzt" in
u mit der Ablaufrate. Für chemischen Kraftstoff ist er begrenzt durch (und in erster Näherung gleich)
u = √ (2
q ), wobei
q die spezifische Verbrennungswärme ist. Welches ist der Energiegehalt pro Kilogramm. Und wenn dieses
q „zu kurz kommt“, stellt sich heraus, dass das Massenverhältnis am Anfang und am Ende exponentiell groß ist:
M /
m = e
V / √ (2 q ) [3]
Oder
V = Ln (
M /
m ) * √ (
2q ) [3a]
Ein paar Anmerkungen, für Nerds und zur Klarheit1. Ja, es gibt genauere Ausdrücke für die Durchflussrate als
u = √ (
2q ). Als ich den Kredit für sie weitergab, "übergab" Gorbatschow die UdSSR. Diese Formeln sind jedoch kompliziert, erschrecken die Leser und berücksichtigen Effekte, die hier nicht wichtig sind.
u = √ (
2q ) beschreibt die Abhängigkeit von Interesse für uns angemessen, obwohl sie die Antwort um 10-30% überbewertet. Und ja, es gibt so etwas wie einen bestimmten Impuls, aber in diesem speziellen Artikel ist die Durchflussrate bequemer zu verwenden.
2. Grundsätzlich verbietet nichts einer chemischen Rakete, eine Ausströmgeschwindigkeit
u höher als √ (2
q ) zu erreichen. Wie? Nehmen wir an, wir verbrennen Kraftstoff nicht in einer Düse, sondern in einem Generator und erzeugen elektrische Energie. Beschleunigen Sie dann mit dieser Energie den Anteil
x des Abgases (0 <
x ≤ 1) auf sehr hohe Geschwindigkeiten. Zum Beispiel ein Plasma-Elektrostrahltriebwerk
[ 230 ] . Und die Abgasrückstände werden dumm bei Nullgeschwindigkeit abgeladen. Der Einfachheit halber nehmen wir an, dass alle Transformationen ohne Energieverlust mit 100% Wirkungsgrad ablaufen. Wird eine solche Rakete mit einem festen Massenverhältnis
M /
m auf eine höhere Geschwindigkeit
V beschleunigen (d. H. Wird sie effektiver sein)?
Die Antwort ist nein. Es ist einfach, die Gleichungen zu lösen, die die Bewegung einer solchen Rakete beschreiben, und zu erhalten:
V = Ln (
M /
m ) * √ (
2qx )
Das heißt, seine Endgeschwindigkeit beträgt nur √
x von der typisierten „normalen“ Rakete mit direkter Kraftstoffverbrennung (vgl. [3a]). Und diese Geschwindigkeit ist immer noch fest an
q gebunden.
3. Was ist, wenn die Rakete nicht mit Kraftstoff, sondern mit Batterie arbeitet? Nun, es sei ein separates Arbeitsmedium mit der Masse
m f an Bord und separat eine Batterie mit einer Energiereserve
E und einer Masse
m b .
Das erste, was Sie hier verstehen müssen, ist, dass die Batterie aus vielen kleinen „Modulen“ bestehen muss, die während des Trainings zurückgesetzt werden. Andernfalls tragen wir die "tote" Ladung leerer Batterien mit uns. Wenn ja, dann unterscheidet sich dies konzeptionell nicht von normalem Kraftstoff an Bord mit einer Gesamtenergiereserve
E und einer Masse
m f +
m b . Und wenn
q =
E / (
m f +
m b ) eines solchen Systems niedriger ist als das einer herkömmlichen chemischen Rakete, dann fliegt es nicht besser ab.
5. Aber was ist mit elektrischen Raketentriebwerken
[ 225 ] ? Immerhin geben sie Durchflussraten von zehn und hundert Kilometern pro Sekunde an und führten erfolgreiche interplanetare Manöver mit sehr bescheidenen
M /
m- Verhältnissen durch. Wie so? Tatsache ist, dass ERDs offene Systeme sind. Sie tragen die Arbeitsflüssigkeit (Quecksilber, Xenon usw.) mit sich. Aber Energie ist nicht. Energie kommt von Sonnenkollektoren. Wenn sie stattdessen gewöhnliche Batterien mit einem Energiegehalt der Masse
q tragen würden , wäre ihr Wirkungsgrad gemäß der Formel [3a] nicht höher.
Der Artikel wurde für die Website https://habr.com geschrieben . Bitte beachten Sie beim Kopieren die Quelle. Der Autor des Artikels ist Evgeny Bobukh .Raketen sind also teuer, weil ihr extrem leichtes „trockenes“ Design einer extrem schweren Last, hauptsächlich Treibstoff, standhalten muss (und sie sogar schnell durch die TNA „pumpt“). Und die Ladung ist großartig, weil unser Kraftstoff zu schwer ist. Es wird sehr wenig Joule pro Kilogramm hineingelegt.
Lassen Sie uns nun die Gründe für diese Einschränkung verstehen.
Warum sollte man sich die Reaktion der Wasserstoffverbrennung in Fluor als eine der einfachsten genauer ansehen? Darin tauschen die Wasserstoff-Wasserstoff- und Fluor-Fluor-Paare Partner aus, wodurch zwei Wasserstoff-Fluor-Paare entstehen:
H 2 +
F 2 = 2
HFWoher kommt die freigesetzte Energie?
Ein Wasserstoffmolekül hat zwei Atome. Atome haben Elektronen. Sie werden in Form einer Art Wolke um das Atom "verschmiert" und sind hauptsächlich durch elektrostatische Anziehung mit dem Kern verbunden. Elektronen sind extern, Valenz und (außer Wasserstoff) intern und nehmen nicht an chemischen Reaktionen teil. Nach der Reaktion wechseln Wasserstoff und Fluor die Plätze. Elektrische Wolken von Valenzelektronen werden neu verteilt und ändern leicht ihre Form. So etwas wie das:
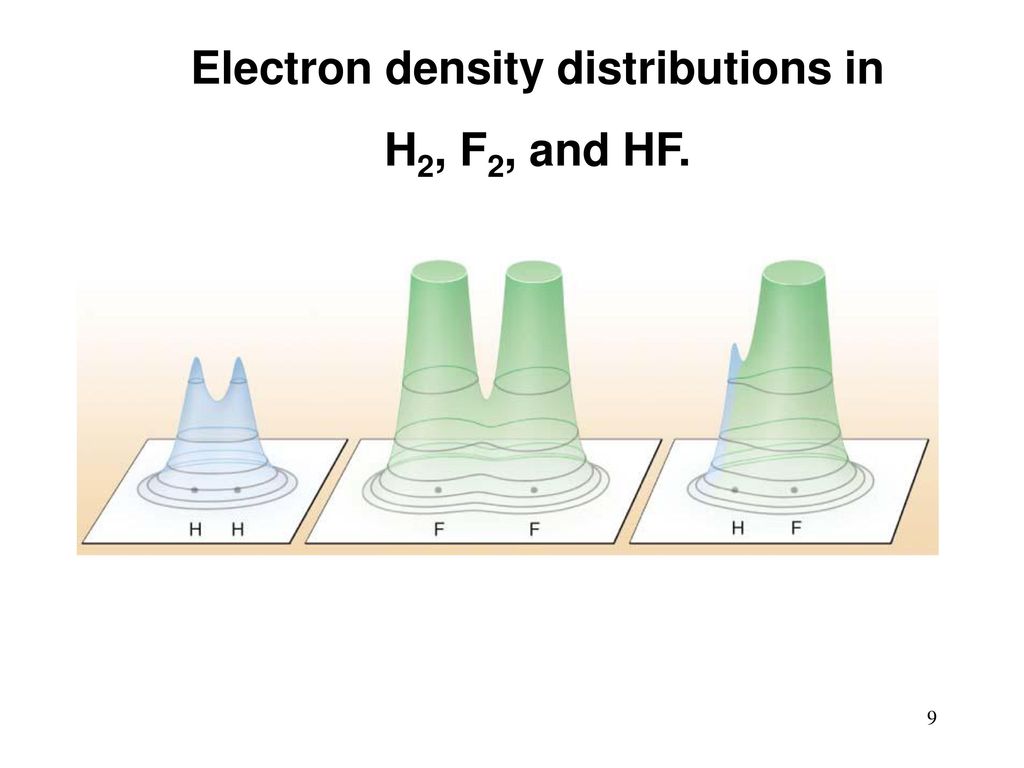
[Bildnachweis [
295 ]]
Die potentielle Bindungsenergie von Elektronen mit Atomen in neuen Wolken ist unterschiedlich. In diesem Fall (diese Energie ist negativ) ist sie jetzt kleiner als die von
H 2 und
F 2 getrennt. Wo ist der Unterschied geblieben? Die kinetische Energie eines Moleküls, die Schwingungen seiner Atome, elektromagnetische Strahlung. All dies wurde schließlich zu Hitze. Was das Gas ausdehnte und Traktion gab.
Und hier ist der kritische Moment. An chemischen Reaktionen sind nur externe Valenzelektronen beteiligt. Die Dichteverteilung anderer Elektronen (sowie das elektrische Feld „in der Tiefe“ des Atoms) bleiben praktisch unverändert. Bei chemischen Reaktionen interagieren Atome miteinander wie über "Intermediäre", die Valenzelektronen sind:
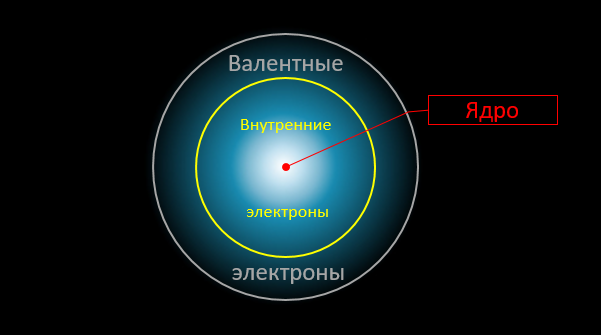
Nun stellt sich die Frage: Was ist die maximal mögliche Energie, die während einer solchen „Permutation“ freigesetzt werden kann? Offensichtlich kann es die Summe der Bindungsenergien externer Elektronen mit Atomen (im End- und Anfangsprodukt) nicht überschreiten. Diese Bindungsenergien sind uns jedoch bekannt
[ 285 ] . Pro Atom betragen sie 1,5 - 25
Elektronenvolt (
eV ) und werden in Bruchteilen der Rydberg-Konstante ausgedrückt - ein Grundwert, der aus den Grundkonstanten unseres Universums konstruiert wird:
Ry (im Gaußschen System) =
m e e 4/2 ħ 2 =
1 3 .6 eV [
300 ]
Darüber hinaus sind sowohl 25 als auch 13,6 eV nicht erreichbar. Denn bei typischen Reaktionen wird bei weitem nicht die gesamte Bindungsenergie freigesetzt, sondern nur der Unterschied zwischen den beiden Konfigurationen, und daher beträgt die praktische Obergrenze für die Energiefreisetzung der Chemie 3-4 eV pro Atom. In Bezug auf ein typisches Kilogramm Kraftstoff + Oxidationsmittel entspricht dies einer freigesetzten Energie von 20 bis 30 MJ. Diese Größe legt die theoretische maximale Gasgeschwindigkeit eines chemischen Strahltriebwerks mit direkter Verbrennung fest.
U = √ (2
q ) = √ (2 * 2,5 * 10
7 ) ≈ 7000 m / s. Natürlich unerreichbar, da Verluste an inneren Freiheitsgraden von Molekülen, Dissoziation, Strahlung, ungerichtete thermische Bewegung usw. nicht berücksichtigt werden.
Es mag den Anschein haben, dass tabellarische Verbrennungswärmen
[ 240 ] (z. B. 120 MJ / kg für Wasserstoff) der oben angegebenen Zahl widersprechen. Tatsache ist jedoch, dass diese Erhitzungen normalerweise pro Kilogramm
Kraftstoff angegeben werden , ohne das für seine Verbrennung erforderliche Oxidationsmittel zu berücksichtigen. Die Rakete trägt beide Komponenten mit sich, und wenn Sie die freigesetzte Energie pro Kilogramm des
Gemisches (bei ausgeglichener Verbrennung) neu berechnen, ergibt sich ein völlig anderes Bild
[ 240 ] [ 250 ] [ 260 ] :
| Kraftstoff + Oxidationsmittel | Reaktion | Heizwert pro kg. Kraftstoff, MJ / kg | 1 kg Kraftstoff benötigt ein Oxidationsmittel, kg. | Brennwert MJ / kg | Die Ausgabe pro Atom der Mischung, eV |
| Wasserstoff + Sauerstoff | 2H 2 + O 2 = 2H 2 O. | 120 | 8 | 13.3 | 0,83 |
| Kerosin + Sauerstoff | 2C 12 H 26 + 37O 2 = 24CO 2 + 26H 2 O. | 43 | 3.5 | 9.6 | 1,02 |
| Kohle + Sauerstoff | C + O 2 = CO 2 | 33 | 2.7 | 9.0 | 1,38 |
| Lithium + Sauerstoff | 4Li + O 2 = 2Li 2 O. | 43.5 | 1.2 | 20.2 | 2.10 |
| Bor + Sauerstoff | 2B + 1,5O 2 = B 2 O 3 | 57.2 | 2.2 | 17.8 | 2.58 |
| Magnesium + Sauerstoff | 2 mg + O 2 = 2 mg | 25.1 | 0,7 | 15.1 | 3.18 |
| Beryllium + Sauerstoff | 2Be + O 2 = 2BeO | 66.6 | 1.8 | 24.0 | 3.12 |
| Lithium + Fluor | 2Li + F 2 = 2LiF | 88,8 | 2.7 | 23.7 | 3.21 |
| Beryllium + Fluorid | Be + F 2 = BeF 2 | 114 | 4.2 | 21.9 | 3.57 |
| Dicyanoacetylen + Ozon | C 4 N 2 + (4/3) O 3 = 4CO + N 2 | 16.2 | 0,8 | 8.8 | 1.28 |
Wie Sie sehen können, geben Kraftstoffe selbst bei den energieintensivsten, wenn auch für den praktischen Gebrauch ungeeigneten Brennstoffen während der Verbrennung nur 24 MJ / kg Wärme ab. Und wir sind fast seit Beginn der Astronautik an diese Grenze gestoßen, die eine grafische Darstellung der Abflussrate chemischer Motoren in Abhängigkeit vom Jahr ihrer Entstehung zeigt:

[Frühe Motoren nach [
310 ], [
320 ], [
330 ], später - Wikipedia einzeln. Datenerfassung
hier ]
Es scheint, dass das Potenzial von chemischem Kraftstoff seit langem entwickelt wurde. Ist es möglich, Energie in einer anderen Form zu speichern?
Fortsetzung folgt.