👏🏿 ⏲️ 🍺 Huffman-Datenkomprimierung 🤔 ㊗️ 🍝

Eintrag

In diesem Artikel werde ich über den bekannten Huffman-Algorithmus sowie dessen Anwendung bei der Datenkomprimierung sprechen.

Als Ergebnis werden wir einen einfachen Archivierer schreiben. Es gab bereits einen Artikel über Habré , jedoch ohne praktische Umsetzung. Das theoretische Material des aktuellen Beitrags stammt aus dem Schulunterricht in Informatik und aus Robert Lafores Buch „Datenstrukturen und Algorithmen in Java“. Also ist alles unter dem Schnitt!

Ein kleiner Gedanke

In einer Nur-Text-Datei wird ein Zeichen mit 8 Bit (ASCII-Codierung) oder 16 Bit (Unicode-Codierung) codiert. Weiter werden wir die ASCII-Codierung betrachten. Nehmen Sie zum Beispiel die Zeile s1 = "SUSIE SAGT, ES IST EINFACH \ n". Insgesamt enthält die Zeile natürlich 22 Zeichen, einschließlich Leerzeichen und des Zeilenumbruchzeichens '\ n'. Eine Datei mit dieser Zeile wiegt 22 * 8 = 176 Bit. Es stellt sich sofort die Frage: Ist es sinnvoll, alle 8 Bits zum Codieren von 1 Zeichen zu verwenden? Wir verwenden nicht alle ASCII-Zeichen. Selbst wenn es verwendet wird, wäre es rationaler, wenn der häufigste Buchstabe - S - den kürzestmöglichen Code und der seltenste Buchstabe - T (oder U oder '\ n') - einen authentischeren Code angibt. Dies ist der Huffman-Algorithmus: Sie müssen die beste Codierungsoption finden, bei der die Datei ein minimales Gewicht hat. Es ist ganz normal, dass die Codelängen für verschiedene Zeichen unterschiedlich sind - dies ist die Grundlage des Algorithmus.

Codierung

Warum geben Sie dem Zeichen 'S' keinen Code, zum Beispiel 1 Bit lang: 0 oder 1. Lassen Sie es 1 sein. Dann geben wir das am zweithäufigsten angetroffene Zeichen - '' (Leerzeichen) - 0. Stellen Sie sich vor, Sie haben begonnen, Ihre Nachricht zu dekodieren - codierte Zeichenfolge s1 - und Sie sehen, dass der Code mit 1 beginnt. Was ist also zu tun: Ist es ein Zeichen S oder ein anderes Zeichen, zum Beispiel A? Daher ergibt sich eine wichtige Regel:

Kein Code sollte ein Präfix eines anderen sein

Diese Regel ist der Schlüssel im Algorithmus. Daher beginnt die Erstellung des Codes mit der Häufigkeitstabelle, die die Häufigkeit (Anzahl der Vorkommen) jedes Zeichens angibt:

Die Zeichen mit den meisten Vorkommen sollten mit der kleinstmöglichen Anzahl von Bits codiert werden. Ich werde ein Beispiel für eine der möglichen Codetabellen geben:

Die verschlüsselte Nachricht sieht also folgendermaßen aus:

10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110

Ich habe den Code jedes Zeichens durch ein Leerzeichen getrennt. Dies wird in einer komprimierten Datei nicht wirklich passieren!
Es stellt sich die Frage: ~~Wie kam diese Salaga auf einen Code~~ ? Wie erstelle ~~ich~~ eine Codetabelle? Dies wird unten diskutiert.

Einen Huffman-Baum bauen

Hier kommen binäre Suchbäume zur Rettung. Keine Sorge, hier sind die Methoden zum Suchen, Einfügen und Löschen nicht erforderlich. Hier ist die Baumstruktur in Java:

 public class Node { private int frequence; private char letter; private Node leftChild; private Node rightChild; ... }

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } ... }

Dies ist kein vollständiger Code, der vollständige Code wird unten angegeben.

Hier ist der Baumbildungsalgorithmus selbst:

Erstellen Sie für jedes Zeichen aus der Nachricht ein Knotenobjekt (Zeile s1). In unserem Fall gibt es 9 Knoten (Knotenobjekte). Jeder Knoten besteht aus zwei Datenfeldern: Symbol und Frequenz
Erstellen Sie für jeden Knotenknoten ein Baumobjekt (BinaryTree). Der Knoten wird zur Wurzel des Baums.
Fügen Sie diese Bäume in die Prioritätswarteschlange ein. Je niedriger die Frequenz, desto höher die Priorität. Daher wird beim Extrahieren der Dervo immer mit der niedrigsten Frequenz ausgewählt.

Als nächstes müssen Sie zyklisch Folgendes tun:

Extrahieren Sie zwei Bäume aus der Prioritätswarteschlange und machen Sie sie zu Nachkommen des neuen Knotens (des neu erstellten Knotens ohne Buchstaben). Die Frequenz des neuen Knotens ist gleich der Summe der Frequenzen zweier Nachkommenbäume.
Erstellen Sie für diesen Knoten einen Baum mit einer Wurzel in diesem Knoten. Fügen Sie diesen Baum wieder in die Prioritätswarteschlange ein. (Da der Baum eine neue Frequenz hat, wird er höchstwahrscheinlich an einen neuen Platz in der Warteschlange gelangen.)
Fahren Sie mit den Schritten 1 und 2 fort, bis nur noch ein Baum in der Warteschlange vorhanden ist - der Huffman-Baum

Betrachten Sie diesen Algorithmus in Zeile s1:

Hier zeigt das Symbol "lf" (Zeilenvorschub) den Übergang zu einer neuen Zeile an, "sp" (Leerzeichen) ist ein Leerzeichen.

Was kommt als nächstes?

Wir haben einen Huffman-Baum. Na gut. Und was soll man damit machen? ~~Sie werden es nicht kostenlos nehmen.~~ Und dann müssen Sie alle möglichen Wege von der Wurzel bis zu den Blättern des Baumes verfolgen. Lassen Sie uns vereinbaren, die Kante 0 zu bezeichnen, wenn sie zum linken Nachkommen führt, und 1, wenn sie zum rechten Nachkommen führt. Genau genommen ist in diesen Notationen der Symbolcode der Pfad von der Wurzel des Baums zu dem Blatt, das dasselbe Symbol enthält.

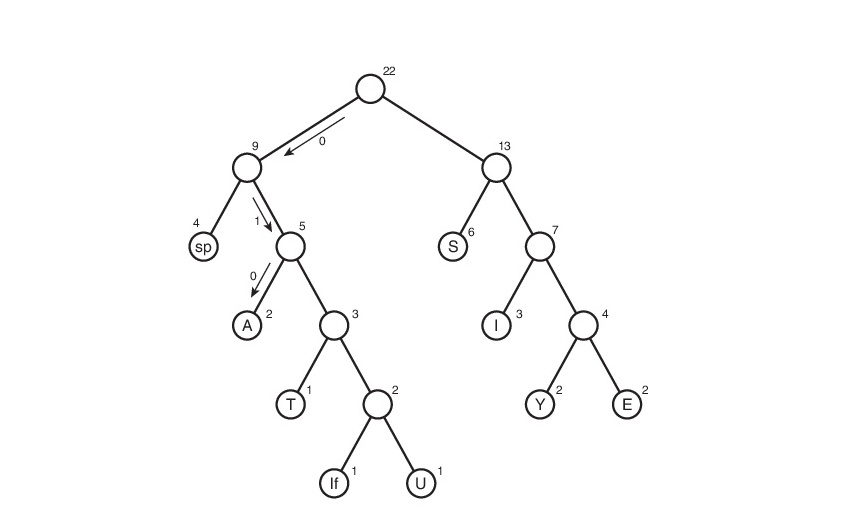
Somit stellte sich die Codetabelle heraus. Beachten Sie, dass wir, wenn wir diese Tabelle betrachten, auf das "Gewicht" jedes Zeichens schließen können - dies ist die Länge seines Codes. Dann wiegt die komprimierte Datei: 2 * 3 + 2 * 4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 Bit. Anfangs wog es 176 Bit. Deshalb haben wir es um das 176/65 = 2,7-fache reduziert! Aber das ist Utopie. Es ist unwahrscheinlich, dass ein solcher Koeffizient erhalten wird. Warum? Dies wird etwas später besprochen.

Dekodierung

Nun, vielleicht ist das Einfachste, was noch übrig ist, das Dekodieren. Ich denke, viele von Ihnen haben vermutet, dass es unmöglich ist, einfach eine komprimierte Datei zu erstellen, ohne einen Hinweis darauf zu haben, wie sie codiert wurde - wir können sie nicht dekodieren! Ja, es war schwer für mich, dies zu realisieren, aber ich musste eine Textdatei table.txt mit einer Komprimierungstabelle erstellen:

 01110 00 A010 E1111 I110 S10 T0110 U01111 Y1110

Notieren Sie die Tabelle in Form von "Zeichen" "Zeichencode". Warum ist 01110 ohne Zeichen? Tatsächlich ist es mit einem Symbol, nur den Java-Werkzeugen, die ich bei der Ausgabe in eine Datei verwendet habe, das Zeilenumbruchzeichen - '\ n' - wird in einen Zeilenumbruch konvertiert (egal wie dumm es klingt). Daher ist die leere Zeile oben das Zeichen für Code 01110. Bei Code 00 ist das Zeichen ein Leerzeichen am Zeilenanfang. Ich muss sofort sagen, dass ~~unsere~~ Methode zur Speicherung dieser Tabelle die irrationalste sein kann. Aber es ist einfach zu verstehen und umzusetzen. Ich freue mich über Ihre Empfehlungen in den Kommentaren zur Optimierung.

Diese Tabelle zu haben ist sehr einfach zu dekodieren. Erinnern Sie sich daran, nach welcher Regel wir uns beim Erstellen der Codierung orientiert haben:

Kein Code sollte einem anderen vorangestellt werden

Hier spielt es eine unterstützende Rolle. Wir lesen nacheinander Stück für Stück und sobald die empfangene Zeichenfolge d, die aus Lesebits besteht, mit der Codierung übereinstimmt, die dem Zeichen entspricht, wissen wir sofort, dass das Zeichen codiert wurde (und nur es!). Als nächstes schreiben wir ein Zeichen in die Decodierungszeile (die Zeile, die die decodierte Nachricht enthält), setzen die Zeile d auf Null und lesen dann die codierte Datei.

Implementierung

Es ist Zeit, ~~meinen Code~~ zu ~~demütigen, indem ich~~ einen Archivierer schreibe. Nennen wir es Compressor.

Beginnen wir von vorne. Zuerst schreiben wir die Node-Klasse:

 public class Node { private int frequence;// private char letter;// private Node leftChild;//  private Node rightChild;//  public Node(char letter, int frequence) { //,  this.letter = letter; this.frequence = frequence; } public Node() {}//    (.       ) public void addChild(Node newNode) {//  if (leftChild == null)//  =>  =>    leftChild = newNode; else { if (leftChild.getFrequence() <= newNode.getFrequence()) // ,   rightChild = newNode;// ,     else { rightChild = leftChild; leftChild = newNode; } } frequence += newNode.getFrequence();//  } public Node getLeftChild() { return leftChild; } public Node getRightChild() { return rightChild; } public int getFrequence() { return frequence; } public char getLetter() { return letter; } public boolean isLeaf() {//   return leftChild == null && rightChild == null; } }

Nun der Baum:

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } public int getFrequence() { return root.getFrequence(); } public Node getRoot() { return root; } }

Prioritätswarteschlange:

 import java.util.ArrayList;//-,      class PriorityQueue { private ArrayList<BinaryTree> data;//  private int nElems;//-    public PriorityQueue() { data = new ArrayList<BinaryTree>(); nElems = 0; } public void insert(BinaryTree newTree) {// if (nElems == 0) data.add(newTree); else { for (int i = 0; i < nElems; i++) { if (data.get(i).getFrequence() > newTree.getFrequence()) {//     data.add(i, newTree);// . ,  c       1  break;//       } if (i == nElems - 1) data.add(newTree); } } nElems++;// -   1 } public BinaryTree remove() {//   BinaryTree tmp = data.get(0);//   data.remove(0);//,  nElems--;// -   1 return tmp;//  (   ) } }

Die Klasse, die den Huffman-Baum erstellt:

 public class HuffmanTree { private final byte ENCODING_TABLE_SIZE = 127;//   private String myString;// private BinaryTree huffmanTree;//  private int[] freqArray;//  private String[] encodingArray;//  //----------------constructor---------------------- public HuffmanTree(String newString) { myString = newString; freqArray = new int[ENCODING_TABLE_SIZE]; fillFrequenceArray(); huffmanTree = getHuffmanTree(); encodingArray = new String[ENCODING_TABLE_SIZE]; fillEncodingArray(huffmanTree.getRoot(), "", ""); } //--------------------frequence array------------------------ private void fillFrequenceArray() { for (int i = 0; i < myString.length(); i++) { freqArray[(int)myString.charAt(i)]++; } } public int[] getFrequenceArray() { return freqArray; } //------------------------huffman tree creation------------------ private BinaryTree getHuffmanTree() { PriorityQueue pq = new PriorityQueue(); //   for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) {//     Node newNode = new Node((char) i, freqArray[i]);//    Node BinaryTree newTree = new BinaryTree(newNode);//  Node  BinaryTree pq.insert(newTree);//   } } while (true) { BinaryTree tree1 = pq.remove();//    . try { BinaryTree tree2 = pq.remove();//     Node newNode = new Node();//  Node newNode.addChild(tree1.getRoot());//      newNode.addChild(tree2.getRoot()); pq.insert(new BinaryTree(newNode); } catch (IndexOutOfBoundsException e) {//     return tree1; } } } public BinaryTree getTree() { return huffmanTree; } //-------------------encoding array------------------ void fillEncodingArray(Node node, String codeBefore, String direction) {//   if (node.isLeaf()) { encodingArray[(int)node.getLetter()] = codeBefore + direction; } else { fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0"); fillEncodingArray(node.getRightChild(), codeBefore + direction, "1"); } } String[] getEncodingArray() { return encodingArray; } public void displayEncodingArray() {//  fillEncodingArray(huffmanTree.getRoot(), "", ""); System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); } } System.out.println("========================================================"); } //----------------------------------------------------- String getOriginalString() { return myString; } }

Klasse, die enthält, welche codiert / decodiert:

 public class HuffmanOperator { private final byte ENCODING_TABLE_SIZE = 127;//  private HuffmanTree mainHuffmanTree;//  (   ) private String myString;//  private int[] freqArray;//  private String[] encodingArray;//  private double ratio;//  public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress this.mainHuffmanTree = MainHuffmanTree; myString = mainHuffmanTree.getOriginalString(); encodingArray = mainHuffmanTree.getEncodingArray(); freqArray = mainHuffmanTree.getFrequenceArray(); } public HuffmanOperator() {}//for extract; //---------------------------------------compression----------------------------------------------------------- private String getCompressedString() { String compressed = ""; String intermidiate = "";// (  ) //System.out.println("=============================Compression======================="); //displayEncodingArray(); for (int i = 0; i < myString.length(); i++) { intermidiate += encodingArray[myString.charAt(i)]; } //      .       8=> //    ( 1,  ) byte counter = 0;//     (   : 0<=counter<8<127) for (int length = intermidiate.length(), delta = 8 - length % 8; counter < delta ; counter++) {//delta -    intermidiate += "0"; } // -         compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate; //  setCompressionRatio(); //System.out.println("==============================================================="); return compressed; } private void setCompressionRatio() {//   double sumA = 0, sumB = 0;//A-the original sum for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { sumA += 8 * freqArray[i]; sumB += encodingArray[i].length() * freqArray[i]; } } ratio = sumA / sumB; } public byte[] getBytedMsg() {//final compression StringBuilder compressedString = new StringBuilder(getCompressedString()); byte[] compressedBytes = new byte[compressedString.length() / 8]; for (int i = 0; i < compressedBytes.length; i++) { compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2); } return compressedBytes; } //---------------------------------------end of compression---------------------------------------------------------------- //------------------------------------------------------------extract----------------------------------------------------- public String extract(String compressed, String[] newEncodingArray) { String decompressed = ""; String current = ""; String delta = ""; encodingArray = newEncodingArray; //displayEncodingArray(); // -   for (int i = 0; i < 8; i++) delta += compressed.charAt(i); int ADDED_ZEROES = Integer.parseInt(delta, 2); for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) { //i = 8, ..      -   current += compressed.charAt(i); for (int j = 0; j < ENCODING_TABLE_SIZE; j++) { if (current.equals(encodingArray[j])) {//  decompressed += (char)j;//   current = "";//    } } } return decompressed; } public String getEncodingTable() { String enc = ""; for (int i = 0; i < encodingArray.length; i++) { if (freqArray[i] != 0) enc += (char)i + encodingArray[i] + '\n'; } return enc; } public double getCompressionRatio() { return ratio; } public void displayEncodingArray() {//  System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { //if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); //} } System.out.println("========================================================"); } }

Klasse, die das Schreiben in eine Datei erleichtert:

 import java.io.File; import java.io.PrintWriter; import java.io.FileNotFoundException; import java.io.FileOutputStream; import java.io.IOException; import java.io.Closeable; public class FileOutputHelper implements Closeable { private File outputFile; private FileOutputStream fileOutputStream; public FileOutputHelper(File file) throws FileNotFoundException { outputFile = file; fileOutputStream = new FileOutputStream(outputFile); } public void writeByte(byte msg) throws IOException { fileOutputStream.write(msg); } public void writeBytes(byte[] msg) throws IOException { fileOutputStream.write(msg); } public void writeString(String msg) { try (PrintWriter pw = new PrintWriter(outputFile)) { pw.write(msg); } catch (FileNotFoundException e) { System.out.println(" ,     !"); } } @Override public void close() throws IOException { fileOutputStream.close(); } public void finalize() throws IOException { close(); } }

Klasse, die das Lesen aus einer Datei erleichtert:

 import java.io.FileInputStream; import java.io.EOFException; import java.io.BufferedReader; import java.io.InputStreamReader; import java.io.Closeable; import java.io.File; import java.io.IOException; public class FileInputHelper implements Closeable { private FileInputStream fileInputStream; private BufferedReader fileBufferedReader; public FileInputHelper(File file) throws IOException { fileInputStream = new FileInputStream(file); fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream)); } public byte readByte() throws IOException { int cur = fileInputStream.read(); if (cur == -1)//   throw new EOFException(); return (byte)cur; } public String readLine() throws IOException { return fileBufferedReader.readLine(); } @Override public void close() throws IOException{ fileInputStream.close(); } }

Nun, und die Hauptklasse:

 import java.io.File; import java.nio.charset.MalformedInputException; import java.io.FileNotFoundException; import java.io.IOException; import java.nio.file.Files; import java.nio.file.NoSuchFileException; import java.nio.file.Paths; import java.util.List; import java.io.EOFException; public class Main { private static final byte ENCODING_TABLE_SIZE = 127; public static void main(String[] args) throws IOException { try {//       if (args[0].equals("--compress") || args[0].equals("-c")) compress(args[1]); else if ((args[0].equals("--extract") || args[0].equals("-x")) && (args[2].equals("--table") || args[2].equals("-t"))) { extract(args[1], args[3]); } else throw new IllegalArgumentException(); } catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) { System.out.println("    "); System.out.println(" Readme.txt"); e.printStackTrace(); } } public static void compress(String stringPath) throws IOException { List<String> stringList; File inputFile = new File(stringPath); String s = ""; File compressedFile, table; try { stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath())); } catch (NoSuchFileException e) { System.out.println(" ,     !"); return; } catch (MalformedInputException e) { System.out.println("    "); return; } for (String item : stringList) { s += item; s += '\n'; } HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s)); compressedFile = new File(inputFile.getAbsolutePath() + ".cpr"); compressedFile.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) { fo.writeBytes(operator.getBytedMsg()); } //create file with encoding table: table = new File(inputFile.getAbsolutePath() + ".table.txt"); table.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(table)) { fo.writeString(operator.getEncodingTable()); } System.out.println("   : " + compressedFile.getAbsolutePath()); System.out.println("    " + table.getAbsolutePath()); System.out.println("     !"); double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//  double realRatio = Math.round((double) inputFile.length() / ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//  System.out.println("    " + idealRatio); System.out.println("      " + realRatio); } public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException { HuffmanOperator operator = new HuffmanOperator(); File compressedFile = new File(filePath), tableFile = new File(tablePath), extractedFile = new File(filePath + ".xtr"); String compressed = ""; String[] encodingArray = new String[ENCODING_TABLE_SIZE]; //read compressed file //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here: try (FileInputHelper fi = new FileInputHelper(compressedFile)) { byte b; while (true) { b = fi.readByte();//method returns EOFException compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0"); } } catch (EOFException e) { } //-------------------- //read encoding table: try (FileInputHelper fi = new FileInputHelper(tableFile)) { fi.readLine();//skip first empty string encodingArray[(byte)'\n'] = fi.readLine();//read code for '\n' while (true) { String s = fi.readLine(); if (s == null) throw new EOFException(); encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length()); } } catch (EOFException ignore) {} extractedFile.createNewFile(); //extract: try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) { fo.writeString(operator.extract(compressed, encodingArray)); } System.out.println("    " + extractedFile.getAbsolutePath()); } }

Die Anweisungsdatei readme.txt können Sie selbst schreiben :-)

Fazit

Das ist wahrscheinlich alles, was ich sagen wollte. Wenn Sie etwas über ~~meine Inkompetenz bei~~ Verbesserungen des Codes, des Algorithmus und jeglicher Optimierung im Allgemeinen zu sagen haben, können Sie gerne schreiben. Wenn ich etwas falsch verstanden habe, schreibe auch. Ich würde mich freuen, von Ihnen in den Kommentaren zu hören!

PS

Ja, ja, ich bin immer noch hier, weil ich den Koeffizienten nicht vergessen habe. Für die Zeichenfolge s1 wiegt die Codierungstabelle 48 Byte - viel mehr als die Originaldatei, und sie haben zusätzliche Nullen nicht vergessen (die Anzahl der hinzugefügten Nullen beträgt 7) => das Komprimierungsverhältnis ist kleiner als eins: 176 / (65 + 48 * 8 + 7) = 0,38. Wenn Sie dies auch bemerkt haben, dann sind Sie ~~einfach nicht gut im Gesicht~~ . Ja, diese Implementierung ist für kleine Dateien äußerst ineffizient. Aber was passiert mit großen Dateien? Die Dateigrößen überschreiten die Größe der Codierungstabelle bei weitem. Hier funktioniert der Algorithmus wie er sollte! Zum Beispiel gibt der Archivierer für den Faust-Monolog einen realen (nicht idealisierten) Koeffizienten von 1,46 an - fast das Eineinhalbfache! Und ja, die Datei sollte auf Englisch sein.

Huffman-Datenkomprimierung