XGBoost von Grund auf neu schreiben - Teil 1: Entscheidungsbäume

Hallo Habr!

Nach zahlreichen Suchen nach hochwertigen Anleitungen zu Entscheidungsbäumen und Ensemble-Algorithmen (Boosten, Entscheidungswald usw.) mit ihrer direkten Implementierung in Programmiersprachen und ohne etwas zu finden (wer es findet, schreibe in die Kommentare, vielleicht lerne ich etwas Neues), Ich beschloss, meine eigene Führung zu übernehmen, wie ich es gerne sehen würde. Die Aufgabe in Worten ist einfach, aber wie Sie wissen, steckt der Teufel im Detail, von dem es viele Algorithmen mit Bäumen gibt.

Da das Thema ziemlich umfangreich ist, wird es sehr schwierig sein, alles in einen Artikel zu packen. Daher wird es zwei Veröffentlichungen geben: Die erste ist Bäumen gewidmet, und der zweite Teil ist der Implementierung des Gradientenverstärkungsalgorithmus gewidmet. Das gesamte hier vorgestellte Material wurde basierend auf Open Source, meinem Code, dem Code von Kollegen und Freunden zusammengestellt und gestaltet. Ich warne Sie sofort, es wird viel Code geben.



Was müssen Sie also wissen und lernen können, wie Sie Ihre eigenen Ensemble-Algorithmen mit Entscheidungsbäumen von Grund auf neu schreiben? Da ein Ensemble von Algorithmen nichts anderes als eine Zusammensetzung von „schwachen Algorithmen“ ist, erfordert das Schreiben eines guten Ensembles gute „schwache Algorithmen“. Wir werden sie in diesem Artikel ausführlich analysieren. Wie der Name schon sagt, handelt es sich hierbei um wichtige Bäume. Wenn wir von einfach zu komplex wechseln, lernen wir, wie man sie schreibt. In diesem Fall wird der Schwerpunkt direkt auf die Implementierung gelegt, die gesamte Theorie wird in einem Minimum dargestellt, im Grunde werde ich Links zu Materialien für unabhängige Studien geben.

Um das Material zu lernen, müssen Sie verstehen, wie gut oder schlecht unser Algorithmus ist. Wir werden sehr einfach verstehen - wir werden einen bestimmten Datensatz reparieren und unsere Algorithmen mit den Algorithmen von Bäumen von Sklearn vergleichen (nun, was würde ohne diese Bibliothek passieren). Wir werden viel vergleichen: die Komplexität des Algorithmus, Metriken für Daten, Betriebszeit usw.

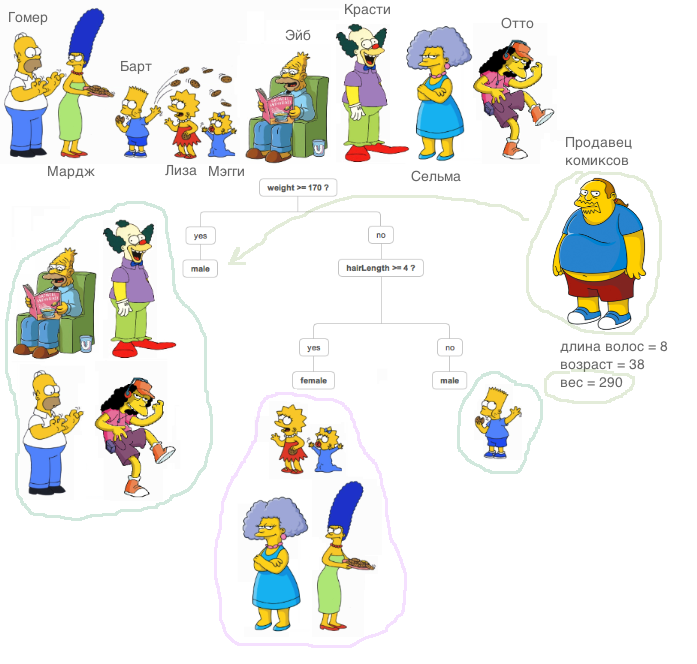
Was ist ein entscheidender Baum? Ein sehr gutes Material, das das Prinzip des Entscheidungsbaums erklärt, ist im ODS-Kurs enthalten (übrigens ein cooler Kurs, den ich allen empfehlen kann, die mit ML vertraut sind).

Eine sehr wichtige Erklärung: In allen unten beschriebenen Fällen sind alle Vorzeichen real, wir führen keine speziellen Transformationen mit Daten außerhalb der Algorithmen durch (wir vergleichen Algorithmen, keine Datensätze).

Lassen Sie uns nun lernen, wie Sie das Problem der Regression mithilfe von Entscheidungsbäumen lösen. Wir werden die MSE- Metrik als Entropie verwenden.

Wir implementieren eine sehr einfache RegressionTree Klasse, die auf einem rekursiven Ansatz basiert. Absichtlich beginnen wir mit einer sehr ineffektiven, aber leicht verständlichen Implementierung dieser Klasse, damit wir sie in Zukunft verbessern können.

1. RegressionTree () -Klasse

 class RegressionTree(): '''  RegressionTree   .    ,      . ''' def __init__(self, max_depth=3, n_epoch=10, min_size=8): '''   . ''' self.max_depth = max_depth #   self.min_size = min_size #    self.value = 0 #    (   ) self.feature_idx = -1 #    self.feature_threshold = 0 #    self.left = None #   self.right = None #   def fit(self, X, y): '''   .     . ''' #    self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #       prev_error_left = base_error prev_error_right = 0 #     0 -  if self.max_depth <= 1: return dim_shape = X.shape[1] #       left_value = 0 right_value = 0 #     for feat in range(dim_shape): #   idxs = np.argsort(X[:, feat]) #        N = X.shape[0] N1, N2 = N, 0 thres = 1 #      while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #    if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue # ,         target_right = y[idxs][:thres] target_left = y[idxs][thres:] mean_right = y[idxs][:thres].mean(), mean_left = y[idxs][thres:].mean() #        - #   (  ) left_shape = target_left.shape[0] right_shape = target_right.shape[0] mean_left_array = [mean_left for _ in range(left_shape)] mean_right_array = [mean_right for _ in range(right_shape)] #      prev_error_left = N1/N * mse(target_left, mean_left_array) prev_error_right = N2/N * mse(target_right, mean_right_array) #    ,   if (prev_error_left + prev_error_right < error): if (min(N1,N2) > self.min_size): self.feature_idx = feat self.feature_threshold = x left_value = mean_left right_value = mean_right flag = 1 error = prev_error_left + prev_error_right thres += 1 #     ,  if self.feature_idx == -1: return #   -   ,    #   -     self.left = RegressionTree(self.max_depth - 1) self.left.value = left_value self.right = RegressionTree(self.max_depth - 1) self.right.value = right_value #   idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #  self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): '''     -  ,         self.value -    . ''' if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): '''    -      __predict(). ''' y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Ich werde hier kurz erklären, was jede Methode tut.

Die fit lehrt, wie der Name schon sagt, das Modell. Ein Trainingsmuster wird auf die Eingabe angewendet und ein Baumtrainingsverfahren findet statt. Wenn wir die Zeichen mse , suchen wir nach der besten Partition des Baums, um die Entropie zu reduzieren, in diesem Fall mse . Es ist sehr einfach festzustellen, dass es möglich war, eine gute Aufteilung zu finden. Es reicht aus, zwei Bedingungen zu erfüllen. Wir möchten nicht, dass wenige Objekte in die Partition fallen (Schutz vor Umschulung), und der durchschnittliche Fehler für mse sollte geringer sein als der Fehler, der jetzt im Baum vorhanden ist. Wir suchen nach dem gleichen Gewinn an Informationsgewinn . Nachdem wir alle Zeichen und alle eindeutigen Werte auf diese Weise durchlaufen haben, werden wir alle Optionen durchgehen und die beste Partition auswählen. Und dann rufen wir die empfangenen Partitionen rekursiv auf, bis die Bedingungen zum Verlassen der Rekursion erfüllt sind.

Die __predict Methode erstellt, wie der Name schon sagt, ein Prädikat. Nachdem ein Objekt als Eingabe empfangen wurde, durchläuft es die Knoten des resultierenden Baums. In jedem Knoten sind die Attributnummer und der Wert festgelegt. Je nachdem, welchen Wert die eingehende Methode des Objekts für dieses Attribut verwendet, gehen wir entweder zum rechten Nachkommen oder nach links. bis wir zu dem Blatt kommen, in dem es eine Antwort für dieses Objekt gibt.

Die predict macht dasselbe wie die vorherige Methode, nur für eine Gruppe von Objekten.

Wir importieren den bekannten kalifornischen Heimdatensatz. Dies ist ein regulärer Datensatz mit Daten und einem Ziel zur Lösung des Regressionsproblems.

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) 

Beginnen wir mit dem Vergleich! Lassen Sie uns zunächst sehen, wie schnell der Algorithmus lernt. Wir setzen in Sklearn und uns den einzigen Parameter max_depth , lassen Sie ihn gleich 2 sein.

 %%time A = RegressionTree(2) #    A.fit(X,y) 

 from sklearn.tree import DecisionTreeRegressor %%time model = DecisionTreeRegressor(max_depth=2) #  Sklearn model.fit(X,y) 

Folgendes wird angezeigt:

• Für unseren Algorithmus - CPU-Zeiten: Benutzer 4 Minuten 47 Sekunden, System: 8,25 ms, Gesamt: 4 Minuten 47 Sekunden
  Wandzeit: 4min 47s
• Für Sklearn - CPU-Zeiten: Benutzer 53,5 ms, System: 0 ns, Gesamt: 53,5 ms
  Wandzeit: 53,4 ms

Wie Sie sehen können, lernt der Algorithmus tausende Male langsamer. Was ist der Grund? Lass es uns richtig machen.

Erinnern Sie sich daran, wie das Verfahren zum Finden der besten Partition angeordnet ist. Wie Sie wissen, im allgemeinen Fall mit der Größe von Objekten $$$N$ und mit der Anzahl der Zeichen $$$d$ ist die Schwierigkeit, die beste Aufteilung zu finden $$$O (N * logN * d)$ .

Woher kommt diese Komplexität?

Um den Fehler effizient neu zu berechnen, müssen zunächst alle Spalten sortiert werden, um vor dem Übergeben des Features vom kleinsten zum größten zu wechseln. Wenn wir dies für jedes Merkmal tun, entsteht eine entsprechende Komplexität. Wie Sie sehen können, sortieren wir die Vorzeichen, aber das Problem liegt in der Neuberechnung des Fehlers - jedes Mal, wenn wir die Daten in die mse Methode mse , die für die Zeile funktioniert. Dies macht die Fehlerzählung so ineffizient! Immerhin steigt dann die Schwierigkeit, einen Split zu finden, auf $$$O (N ^ 2 * d)$ für große $$$N$ verlangsamt den Algorithmus enorm. Daher fahren wir reibungslos mit dem nächsten Punkt fort.

2. RegressionTree () -Klasse mit schneller Fehlerzählung

Was muss getan werden, um den Fehler schnell wiederzugeben? Nehmen Sie einen Stift und Papier und malen Sie, wie wir die Formeln ändern sollen.

Angenommen, irgendwann wird bereits ein Fehler berechnet $$$N$ Objekte. Es hat die folgende Formel: $$$\ sum_ {i = 1} ^ n (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$ . Hier ist es notwendig, durch zu teilen $$$N$ aber jetzt lassen wir es weg. Wir wollen diesen Fehler schnell bekommen - $$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2$ Das heißt, werfen Sie den Fehler, den das Element einführt $$$y_i$ zu einem anderen Teil.

Da wir das Objekt werfen, muss der Fehler an zwei Stellen nachgezählt werden - auf der rechten Seite (ohne dieses Objekt) und auf der linken Seite (unter Berücksichtigung dieses Objekts). Aber ohne Verlust der Allgemeinheit werden wir nur eine Formel ableiten, da sie ähnlich sein werden.

Da wir mit mse , hatten wir mse Glück: Es ist ziemlich schwierig, eine schnelle Nachzählung eines Fehlers abzuleiten, aber wenn wir mit anderen Metriken arbeiten (z. B. dem Gini-Kriterium, wenn wir das Klassifizierungsproblem lösen), ist eine schnelle Nachzählung viel einfacher.

Nun, lasst uns anfangen, Formeln abzuleiten!

$$

$$\ sum_ {i = 1} ^ N (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 + (y_N - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$$

Wir werden das erste Mitglied schreiben:

$$

$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i + y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac { Ny_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1 } ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - 2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} + (\ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - (\ frac {y_N - y_i} {N}) ^ 2) = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - \\ - (\ frac {y_N - y_i} { N}) ^ 2)$$

Ugh, nur noch ein bisschen übrig. Es bleibt nur der erforderliche Betrag auszudrücken.

$$

$$\ sum_ {i = 1} ^ {N} (y_i - \ frac {\ sum_ {i = 1} ^ {N} y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \\ \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) (\ frac {y_N - y_i} {N}) - (\ frac {y_N - y_i} {N}) ^ 2) + (y_N - \ sum_ {i = 1} ^ {N} \ frac {y_i} {N}) ^ 2$$

Und dann ist klar, wie der gewünschte Betrag ausgedrückt werden soll. Um den Fehler neu zu berechnen, müssen wir nur die Summe der Elemente rechts und links sowie das neue Element selbst speichern, das am Eingang angekommen ist. Jetzt wird der Fehler nachgezählt $$$O (1)$ .

Nun, lassen Sie uns dies in Code implementieren.

 class RegressionTreeFastMse(): '''  RegressionTree    .        O(1). ''' #    def __init__(self, max_depth=3, min_size=10): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None #   -     def fit(self, X, y): #   -   y self.value = y.mean() #   - mse     (  # ,     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2 ,    -   #   - -    if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return self.left = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Lassen Sie uns die Zeit messen, die jetzt für das Training aufgewendet wird, und mit dem Analogon von Sklearn vergleichen.

 %%time A = RegressionTreeFastMse(4, min_size=5) A.fit(X,y) test_mytree = A.predict(X) test_mytree 

 %%time model = DecisionTreeRegressor(max_depth=4) model.fit(X,y) test_sklearn = model.predict(X) 

• Für unseren Algorithmus erhalten wir - CPU-Zeiten: Benutzer 3,11 s, System: 2,7 ms, Gesamt: 3,11 s
  Wandzeit: 3,11 s.
• Für den Algorithmus von Sklearn - CPU-Zeiten: Benutzer 45,9 ms, System: 1,09 ms, Gesamt: 47 ms
  Wandzeit: 45,7 ms.

Die Ergebnisse sind bereits angenehmer. Lassen Sie uns den Algorithmus weiter verbessern.

3. RegressionTree () -Klasse mit linearen Kombinationen von Merkmalen

In unserem Algorithmus werden die Beziehungen zwischen den Attributen in keiner Weise verwendet. Wir korrigieren ein Merkmal und betrachten nur orthogonale Raumpartitionen. Wie lerne ich, die linearen Beziehungen zwischen den Attributen zu verwenden? Das heißt, nach den besten Partitionen zu suchen, ist nicht so $$$a_ {feat} <x$ und $$$\ sum_ {i = 1} ^ K b_i * a_i <x$ wo $$$K$ - Ist eine Zahl kleiner als die Dimension unseres Raumes?

Es gibt viele Möglichkeiten, ich werde zwei der aus meiner Sicht interessantesten hervorheben. Beide Ansätze sind im Buch Friedman beschrieben (er hat diese Bäume erfunden).

Ich werde ein Bild geben, damit klar ist, was gemeint ist:



Zunächst können Sie versuchen, diese linearen Partitionen algorithmisch zu finden. Es ist klar, dass es unmöglich ist, alle linearen Kombinationen zu sortieren, da es unendlich viele Kombinationen gibt. Daher sollte ein solcher Algorithmus gierig sein, dh bei jeder Iteration das Ergebnis der vorherigen Iteration verbessern. Die Hauptidee dieses Algorithmus kann im Buch gelesen werden. Ich werde hier auch einen Link zum Repository meines Freundes und Kollegen mit der Implementierung dieses Algorithmus hinterlassen.

Zweitens, wenn wir nicht weit von der Idee entfernt sind, die beste orthogonale Partition zu finden, wie ändern wir dann den Datensatz, sodass Informationen über die Beziehung von Merkmalen verwendet werden und die Suche auf orthogonalen Partitionen basiert? Das ist richtig, um die ursprünglichen Funktionen in neue umzuwandeln. Sie können beispielsweise die Summe einer Kombination von Features verwenden und bereits nach Partitionen suchen. Eine solche Methode passt schlechter in das algorithmische Konzept, erfüllt aber ihre Aufgabe - sie sucht nach orthogonalen Partitionen, die sich bereits in einer Art Verbindung von Attributen befinden.

Nun, lassen Sie es uns implementieren - wir werden als neue Features beispielsweise alle Arten von Kombinationen von Feature-Summen hinzufügen $$$i, j$ wo $$$I <j$ . Ich stelle fest, dass die Komplexität des Algorithmus in diesem Fall zunehmen wird, es ist klar, wie oft. Um schneller zu sein, werden wir Cython verwenden.

 %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeCython: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeCython left cpdef RegressionTreeCython right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.averages = averages self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def data_transform(self, np.ndarray[np.float64_t, ndim=2] X, list index_tuples): #   -       for i in index_tuples: #  ,       X = np.hstack((X, X[:, i[0]:(i[1]+1)].sum(axis=1).reshape(X.shape[0],1))) return X def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #        #  ,     if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(combinations(stuff,2)) #    X = self.data_transform(X, index_tuples) #   -   y self.value = y.mean() #   - mse     (  , #     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2    -   #   -      if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 # self.feature_idx -     . #   -  ,    -   #  ,   ,     #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeCython(self.max_depth - 1, averages=0) self.left.value = left_value self.right = RegressionTreeCython(self.max_depth - 1, averages=0) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): #   ,        if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(itertools.combinations(stuff,2)) X = self.data_transform(X, index_tuples) y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

4. Vergleich der Ergebnisse

Vergleichen wir die Ergebnisse. Wir werden drei Algorithmen mit denselben Parametern vergleichen - einen Baum von Sklearn, unseren gewöhnlichen Baum und unseren Baum mit neuen Funktionen. Wir werden unseren Datensatz viele Male in Trainings- und Testsätze unterteilen und den Fehler berechnen.

 from sklearn.model_selection import KFold def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list 

Lassen Sie uns nun alle Algorithmen ausführen.

 import matplotlib.pyplot as plt data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_sklearn_tree = get_metrics(X,y,30,DecisionTreeRegressor(max_depth=4, min_samples_leaf=10)) er_fast_mse_tree = get_metrics(X,y,30,RegressionTreeFastMse(4, min_size=10)) er_averages_tree = get_metrics(X,y,30,RegressionTreeCython(4, min_size=10)) %matplotlib inline data = [er_sklearn_tree, er_fast_mse_tree, er_averages_tree] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Tree', 'Fast Mse Tree', 'Averages Tree']) plt.grid() plt.show() 

Ergebnisse:



Unser regulärer Baum ging an Sklearn verloren (was verständlich ist: Sklearn ist gut optimiert und standardmäßig gibt es noch viele Parameter im Baum, die wir nicht berücksichtigen), aber wenn wir Beträge hinzufügen, wird das Ergebnis angenehmer.

Zusammenfassend: Wir haben gelernt, entscheidende Bäume von Grund auf neu zu schreiben, ihre Leistung zu verbessern und ihre Wirksamkeit an realen Datensätzen zu testen, indem wir sie mit dem Algorithmus von Sklearn verglichen haben. Die hier vorgestellten Methoden schränken jedoch die Verbesserung der Algorithmen nicht ein. Beachten Sie daher, dass der vorgeschlagene Code noch besser gemacht werden kann. Im nächsten Artikel werden wir Boosting basierend auf diesen Algorithmen schreiben.

Alles Erfolg!