XGBoost von Grund auf neu schreiben - Teil 2: Gradientenverstärkung

Hallo allerseits!

Im letzten Artikel haben wir herausgefunden, wie Entscheidungsbäume angeordnet sind, und von Grund auf neu implementiert
Konstruktionsalgorithmus, der gleichzeitig optimiert und verbessert wird. In diesem Artikel werden wir den Gradientenverstärkungsalgorithmus implementieren und am Ende unseren eigenen XGBoost erstellen. Die Erzählung folgt demselben Muster: Wir schreiben einen Algorithmus, beschreiben ihn und fassen ihn zusammen, indem wir die Ergebnisse der Arbeit mit Analoga von Sklearn vergleichen.

In diesem Artikel wird der Schwerpunkt auch auf die Implementierung in Code gelegt. Daher ist es besser, die gesamte Theorie zusammen in einer anderen zu lesen (z. B. im ODS-Kurs ). Wenn Sie die Theorie bereits kennen, können Sie mit diesem Artikel fortfahren, da das Thema ziemlich kompliziert ist.



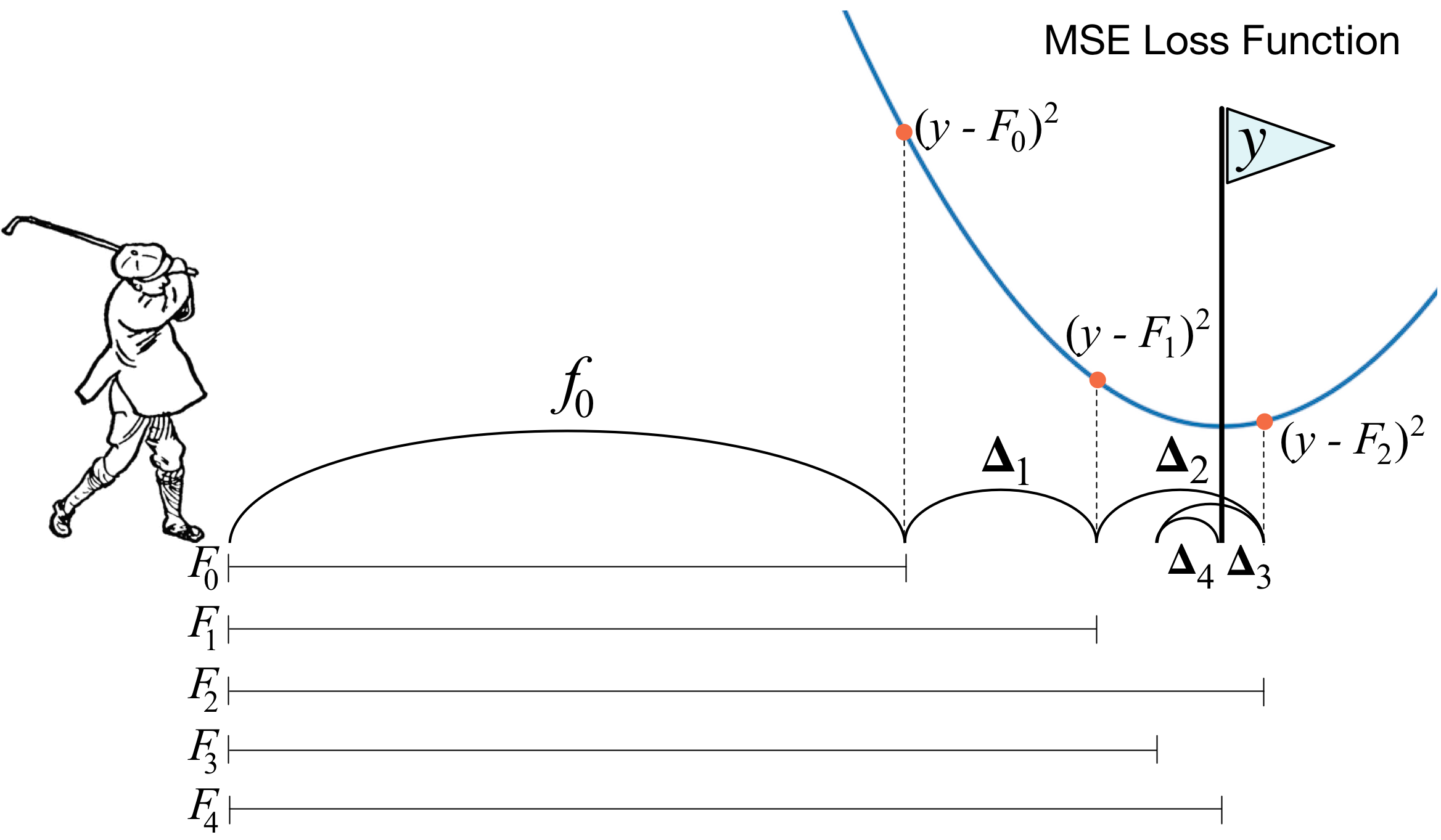
Was ist Gradientenverstärkung? Ein Bild eines Golfspielers beschreibt die Hauptidee perfekt. Um den Ball in das Loch zu treiben, macht der Golfer bei jedem nächsten Schlag die Erfahrung früherer Schläge - für ihn ist dies eine notwendige Voraussetzung, um den Ball in das Loch zu legen. Wenn es sehr unhöflich ist (ich bin kein Meister des Golfsports :)), dann ist bei jedem neuen Schlag das erste, was ein Golfer betrachtet, der Abstand zwischen dem Ball und dem Loch nach dem vorherigen Schlag. Und die Hauptaufgabe ist es, diesen Abstand beim nächsten Schlag zu verringern.

Boosting ist sehr ähnlich aufgebaut. Zunächst müssen wir die Definition von „Loch“ einführen, dh das Ziel, das wir anstreben werden. Zweitens müssen wir lernen zu verstehen, welche Mannschaft wir mit einem Verein schlagen müssen, um näher an das Ziel heranzukommen. Drittens müssen Sie unter Berücksichtigung all dieser Regeln die richtige Reihenfolge der Schläge festlegen, damit jeder nachfolgende den Abstand zwischen dem Ball und dem Loch verringert.

Jetzt geben wir eine etwas strengere Definition. Wir führen das Modell der gewichteten Abstimmung ein:

$$

$$h (x) = \ sum_ {i = 1} ^ nb_ia_i, x \ in X, b_i \ in R$$

Hier $$$X$ Ist der Raum, aus dem wir Objekte nehmen, $$$b_i, a_i$ - Dies ist der Koeffizient vor dem Modell und das Modell selbst, dh der Entscheidungsbaum. Angenommen, es war bereits zu einem bestimmten Zeitpunkt unter Verwendung der beschriebenen Regeln möglich, die Komposition zu ergänzen $$$T-1$ schwacher Algorithmus. Zu lernen zu verstehen, welche Art von Algorithmus im Schritt sein sollte $$$T$ führen wir die Fehlerfunktion ein:

$$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) \ rightarrow min_ {a_T, b_T}$

Es stellt sich heraus, dass der beste Algorithmus derjenige ist, der den bei früheren Iterationen empfangenen Fehler minimieren kann. Und da die Verstärkung ein Gradient ist, muss diese Fehlerfunktion notwendigerweise einen Antigradientenvektor haben, entlang dem Sie sich auf der Suche nach einem Minimum bewegen können. Das ist alles!

Unmittelbar vor der Implementierung werde ich ein paar Worte dazu hinzufügen, wie alles mit uns arrangiert wird. Wie im vorherigen Artikel nehmen wir MSE als Verlust. Berechnen wir den Gradienten:

$$

$$mse (y, vorhersagen) = (y - vorhersagen) ^ 2 \\ \ nabla_ {vorhersagen} mse (y, vorhersagen) = vorhersagen - y$$

Somit ist der Antigradientenvektor gleich $$$y - $ vorhersage$ . Auf dem Schritt $$$i$ Wir betrachten die Fehler des Algorithmus, die bei früheren Iterationen erhalten wurden. Als nächstes trainieren wir unseren neuen Algorithmus auf diese Fehler und fügen ihn dann mit einem Minuszeichen und einem Koeffizienten zu unserem Ensemble hinzu.

Jetzt fangen wir an.

1. Implementierung der üblichen Gradientenverstärkungsklasse

import pandas as pd import matplotlib.pyplot as plt import numpy as np from tqdm import tqdm_notebook from sklearn import datasets from sklearn.metrics import mean_squared_error as mse from sklearn.tree import DecisionTreeRegressor import itertools %matplotlib inline %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeFastMse: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeFastMse left cpdef RegressionTreeFastMse right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #   -   y self.value = y.mean() #   - mse     base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -  ,  ,    delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeFastMse(self.max_depth - 1) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree def fit(self, X, y): self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: #    resid = (y - prediction) #    if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth, min_size = self.min_size) if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth, min_size = self.min_size) #     tree.fit(X, resid) #        b = tree.predict(X).reshape([X.shape[0]]) self.trees_.append(tree) prediction += self.learning_rate * b #       if t > 0: self.loss_by_iter.append(mse(y,prediction)) return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

Wir werden nun die Verlustkurve auf dem Trainingssatz erstellen, um sicherzustellen, dass wir bei jeder Iteration wirklich eine Abnahme haben.

 GDB = GradientBoosting(n_estimators=50) GDB.fit(X,y) x = GDB.predict(X) plt.grid() plt.title('Loss by iterations') plt.plot(GDB.loss_by_iter) 

2. Über entscheidende Bäume sacken

Bevor wir die Ergebnisse vergleichen, lassen Sie uns über das Verfahren zum Absacken von Bäumen sprechen.

Hier ist alles einfach: Wir wollen uns vor Umschulungen schützen und werden daher mit Hilfe von Stichproben mit Rückgabe unsere Vorhersagen mitteln, um nicht versehentlich auf Emissionen zu stoßen (warum dies funktioniert - lesen Sie besser den Link).

 class Bagging(): '''  Bagging -      . ''' def __init__(self, max_depth = 3, min_size=10, n_samples = 10): #super(CART, self).__init__() self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): #      indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): #    self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): #        num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

Nun, als grundlegender Algorithmus können wir nicht nur einen Baum verwenden, sondern von Bäumen einsacken - also werden wir uns wieder vor Umschulungen schützen.

3. Ergebnisse

Vergleichen Sie die Ergebnisse unserer Algorithmen.

 from sklearn.model_selection import KFold import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn import copy def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in tqdm_notebook(kf.split(X)): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' )) er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' )) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1)) %matplotlib inline data = [er_sklearn_boosting, er_boosting, er_boobagg] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag']) plt.grid() plt.show() 

Erhalten:



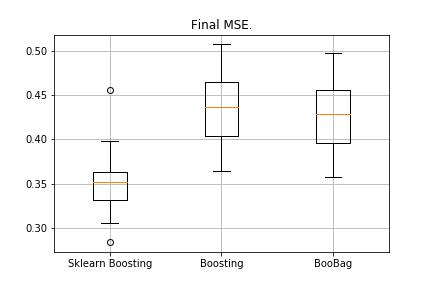
Wir können das Analogon von Sklearn noch nicht besiegen, da wir wiederum nicht viele Parameter berücksichtigen, die bei dieser Methode verwendet werden . Wir sehen jedoch, dass das Absacken ein wenig hilft.

Lassen Sie uns nicht verzweifeln und XGBoost schreiben.

4. XGBoost

Bevor Sie weiterlesen, empfehle ich Ihnen dringend, sich zunächst mit dem nächsten Video vertraut zu machen, das die Theorie sehr gut erklärt.

Erinnern Sie sich daran, welchen Fehler wir beim normalen Boosten minimieren:

$$

$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j))$$

XGBoost fügt dieser Fehlerfunktionalität explizit eine Regularisierung hinzu:

$$

$$err (h) = \ sum_ {j = 1} ^ NL (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) + \ sum_ {i = 1} ^ T \ Omega (a_i)$$

Wie ist diese Funktionalität zu berücksichtigen? Zuerst approximieren wir es mit Hilfe einer Taylor-Reihe zweiter Ordnung, wobei der neue Algorithmus als Inkrement betrachtet wird, entlang dessen wir uns bewegen werden, und dann malen wir bereits, je nachdem, welche Art von Verlust wir haben:

$$$f (x + \ Delta x) \ Dickapprox f (x) + f (x) '\ Delta x + 0,5 * f (x)' '(\ Delta x) ^ 2$

Es ist notwendig zu bestimmen, welchen Baum wir als schlecht und welchen als gut betrachten.

Erinnern Sie sich daran, nach welchem ​​Prinzip die Regression aufgebaut ist $$$L_2$ -regelmäßigkeit - Je normaler die Werte der Koeffizienten vor der Regression sind, desto schlechter ist es daher, dass sie so klein wie möglich sind.

In XGBoost ist die Idee sehr ähnlich: Ein Baum wird mit einer Geldstrafe belegt, wenn die Summe der Norm der Werte in den Blättern darin sehr groß ist. Daher wird die Komplexität des Baums wie folgt eingeführt:

$$

$$\ omega (a) = \ gamma Z + 0,5 * \ sum_ {i = 1} ^ {Z} w_i ^ 2$$

$$$w$ - Werte in den Blättern, $$$Z$ - Anzahl der Blätter.

Das Video enthält Übergangsformeln. Wir werden sie hier nicht anzeigen. Es kommt alles auf die Tatsache an, dass wir eine neue Partition auswählen, um den Gewinn zu maximieren:

$$

$$Gain = \ frac {G_l ^ 2} {S_l ^ 2 + \ lambda} + \ frac {G_r ^ 2} {S_r ^ 2 + \ lambda} - \ frac {(G_l + G_r) ^ 2} {S_l ^ 2 + S_r ^ 2 + \ lambda} - \ gamma$$

Hier $$$\ gamma, \ lambda$ Sind die numerischen Parameter der Regularisierung und $$$G_i, S_i$ - die entsprechenden Summen der ersten und zweiten Ableitung für diese Partition.

Das war's, die Theorie wird sehr kurz formuliert, die Links werden gegeben, jetzt wollen wir darüber sprechen, was die Ableitungen sein werden, wenn wir mit MSE arbeiten. Es ist einfach:

$$$mse (y, vorhersagen) = (y - vorhersagen) ^ 2 \\ \ nabla_ {vorhersagen} mse (y, vorhersagen) = vorhersagen - y \\ \ nabla_ {vorhersagen} ^ 2 mse (y, vorhersagen) = 1$

Wann berechnen wir den Betrag? $$$G_i, S_i$ , einfach zum ersten hinzufügen $$$vorhersagen - y$ und die zweite ist nur die Menge.

 %%cython -a import numpy as np cimport numpy as np cdef class RegressionTreeGain: cdef public int max_depth cdef public np.float64_t gain cdef public np.float64_t lmd cdef public np.float64_t gmm cdef public int feature_idx cdef public int min_size cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef public RegressionTreeGain left cpdef public RegressionTreeGain right def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5): self.max_depth = max_depth self.gmm = gmm self.lmd = lmd self.left = None self.right = None self.feature_idx = -1 self.feature_threshold = 0 self.value = -1e9 self.min_size = min_size return def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef long idx = 0 cpdef long thres = 0 cpdef np.float64_t gl, gr, gn cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 cpdef np.float64_t best_gain = -self.gmm if self.value == -1e9: self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 if self.max_depth <= 1: return dim_shape = X.shape[1] left_value = 0 right_value = 0 #    # -  -   mse, L = (y - pred)**2 # dL/dpred = pred - y,          - # dL^2/d^2pred = 1 - ,       for feat in range(dim_shape): idxs = np.argsort(X[:, feat]) gl,gr = y.sum(),0.0 N1, N2, thres = N, 0, 0 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] gl -= y[idx] gr += y[idx] #   gn = (gl**2) / (N1 + self.lmd) + (gr**2) / (N2 + self.lmd) gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue #     if (gn > best_gain) and (min(N1,N2) > self.min_size): flag = 1 best_gain = gn left_value = -gl / (N1 + self.lmd) right_value = -gr / (N2 + self.lmd) self.feature_idx = feat self.feature_threshold = x thres += 1 self.gain = best_gain if self.feature_idx == -1: return self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.left.value = left_value self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) #    if (self.left.left == None or self.right.left == None): if self.gain < 0.0: self.left = None self.right = None self.feature_idx = -1 def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Eine kleine Klarstellung: Um die Formeln in den Bäumen mit Gewinn schöner zu machen, trainieren wir im Boost das Ziel mit einem Minuszeichen.

Wir modifizieren unser Boosten leicht und passen einige Parameter an. Wenn wir beispielsweise feststellen, dass der Verlust ein Plateau erreicht hat, verringern wir die Lernrate und erhöhen max_depth für die folgenden Schätzer. Wir werden auch eine neue Absackung hinzufügen - jetzt werden wir die Baumbeutel mit Gewinn steigern:

 class Bagging(): def __init__(self, max_depth = 3, min_size=5, n_samples = 10): self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree #  -       #   ,   lr   max_depth self.add_to_max_depth = 1 self.init_mse_board = 1.5 def fit(self, X, y): print (self.base_tree) self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: resid = (y - prediction) if (mse(temp_resid,resid) < self.init_mse_board): self.init_mse_board /= 1.5 self.add_to_max_depth += 1 self.learning_rate /= 1.1 # print ('Alert!', t, self.add_to_max_depth) if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) if self.base_tree == 'XGBoost': tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid tree.fit(X, resid) b = tree.predict(X).reshape([X.shape[0]]) # print (b.shape) self.trees_.append(tree) prediction += self.learning_rate * b temp_resid = resid return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

5. Ergebnisse

Traditionell vergleichen wir die Ergebnisse:

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging')) er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost')) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2)) %matplotlib inline data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost', 'XGBooBag']) plt.grid() plt.show() 

Das Bild sieht wie folgt aus:



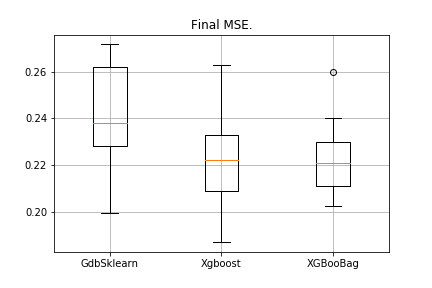
XGBoost hat den niedrigsten Fehler, aber XGBooBag hat einen überfüllten Fehler, was definitiv besser ist: Der Algorithmus ist stabiler.

Das ist alles Ich hoffe wirklich, dass das in zwei Artikeln vorgestellte Material nützlich war und Sie etwas Neues für sich selbst lernen konnten. Mein besonderer Dank gilt Dmitry für umfassendes Feedback und Quellcode, Anton für Ratschläge und Vladimir für schwierige Aufgaben für das Studium.

Alles Erfolg!