Einführung
Bereits im Oktober 2018 erinnerten wir uns gerne an den Adventskalender mit den Aufgaben von 2017 (die Bedingungen sind
hier ) und begannen darüber nachzudenken, was dieses Jahr getan werden kann. Aus mehreren würdigen Ideen haben wir eine Option ausgewählt, bei der wir verschiedene „eingängige“ Aufgaben auswählen, die durch eine schöne Neujahrsgeschichte verbunden sind.
Es war nichts mehr übrig: Aufgaben übernehmen, eine Geschichte verfassen, eine Website mit einer Rangliste erstellen, schön und eng mit Yandex.Constest verbunden, und Anfang Dezember beginnen :-)
Ergebnis
Wie Sie wissen, geht der Appetit mit dem Essen einher, und wir haben uns kopfüber in den Prozess der Erarbeitung des Inhalts von Aufgaben und ihrer technischen Umsetzung gestürzt. Jeder erfolgreiche Fund führte zu weiteren Verbesserungen. Infolgedessen haben wir einen separaten Server für eine der Aufgaben eingerichtet, den anderen zu einem Optimierungsserver gemacht (wir haben immer noch keine genaue Antwort), die Musik selbst aufgenommen und die Distributionen wiederhergestellt - wir haben uns überhaupt nicht gelangweilt!
Das Ergebnis ist:
- 11 Aufgaben (+1 Bonus) mit unterschiedlichem Schwierigkeitsgrad, alle mit Bestätigung im Wettbewerb;
- externe Seite für Teilnehmer ;
- 11 Tage (vom 7. bis einschließlich 17. Dezember) zur Lösung von Problemen.
Interessante Fakten und Geschichten
780 Teilnehmer haben sich angemeldet, 333 Personen haben mit der Lösung begonnen, 203 Personen haben mindestens zwei Aufgaben erfolgreich bestanden.
Zunächst schätzten wir die Nettozeit für die Lösung aller Probleme auf sieben Tage für einen unvorbereiteten Teilnehmer und zwei Tage für einen sehr erfahrenen Teilnehmer (auch bekannt als Absolvent eines neuen CS-Zentrums). Der erste Assistent des Weihnachtsmanns, der alle elf Aufgaben richtig gelöst hatte, war ungefähr einen Tag erledigt, zwei weitere schafften den zweiten!
Brief eines der Teilnehmer: „Guten Tag! Aufgrund Ihres Wettbewerbs habe ich das Büro (40 Personen) speziell für die zweite Aufgabe zum Weihnachtsmannkaffee angehalten. Geben Sie mir bitte einen Hinweis. Wir sind alle sehr gequält. “
Analysieren von Aufgaben
Bedingungen
hier .
Aufgabe D „Musikalische Botschaft“ (Mikhail Plotkin)Es ist sehr einfach, das Problem zu lösen, wenn man nur eine minimale musikalische Ausbildung hat.
Der Versuch, einen Hinweis im rhythmischen Muster zu finden, führte nicht zum Erfolg. Die nächste Idee war, am Klavier zu sitzen und die Melodie aufzunehmen, die Sie gehört haben. Es stellte sich heraus, la, do, mi, si, la, re, salt, mi. In einem Violinschlüssel wie diesem:

Nach den ersten drei Noten folgte eine kurze Pause, als würde die musikalische Phrase in zwei Wörter geteilt. Es blieb nur, Notizen in der traditionellen Buchstabennotation zu schreiben (A = la, B = si, C = do, D = pe, E = mi, F = fa, G = Salz) und zwei Wörter zu öffnen: ACE BADGE.
Ohne Kenntnisse der Musikkompetenz ist es schwieriger, ein Problem zu lösen. Zum Beispiel könnte man ein Programm zum Verarbeiten von Ton verwenden und entweder die Noten selbst oder die Frequenzen von Tönen in Hertz herausfinden und dann herausfinden, welche Frequenzen welchen Noten entsprechen.
Die Aufgabe, die erforderlich ist, um Buchstaben ohne Trennzeichen zusammen zu schreiben, lautet also ACEBADGE.
Aufgabe F „Beutel mit Schneeflocken“ (Mikhail Plotkin)Die Fläche des anfänglichen Dreiecks ist 1. Als nächstes werden im n-ten Schritt t_n Dreiecke hinzugefügt, von denen jedes eine Fläche s_n hat. Die Gesamtfläche der resultierenden Figur wird als Summe einer unendlichen Reihe ausgedrückt:
S = 1 + Σ (t_n * s_n), die Summe über n ist von 0 bis ∞ (1)
Im Nullschritt ist t_0 = 3, s_0 = 1/9, da das Dreieck 3 Seiten hat, auf denen jeweils ein Dreieck mit einer Seite aufgebaut ist, die dreimal kleiner als das Original ist, und daher eine Fläche, die neunmal kleiner als die Fläche des ursprünglichen Dreiecks ist.
Bei jedem nächsten Schritt wird jede Seite zu vier Seiten, die dreimal kleiner sind
t_n = t_ {n-1} * 4 = t_0 * 4n = 3 * 4n,
s_n = s_ {n-1} * (1/9) = s_0 * (1/9) ^ n = 1/9 * (1/9) ^ n.
Daher ist der erforderliche Bereich:
S = 1 + Σ (t_n * s_n) = 1 + 1/3 * Σ ((4/9) ^ n), die Summe über n ist von 0 bis ∞ (2)
Der zweite Term ist die Summe einer unendlich abnehmenden geometrischen Progression. Verwenden Sie zur Berechnung die Schulformel
Σ ((4/9) ^ n) = 1 / (1 - 4/9) = 9/5.
Wenn wir die Formel (2) einsetzen, erhalten wir die Antwort:
S = 1 + 1/3 * 9/5 = 8/5 = 1,6
Aufgabe G und L „Die Route ist gebaut“ (Artyom Romanov)Vielen Dank an Artyom
mehrunesartem für die Lösung! Das Diagramm, das in Problem G verwendet wurde, basiert übrigens auf der Londoner U-Bahn :)
Um dieses Problem zu lösen, verwenden wir eine modifizierte Version der Breitensuche. Wir erhalten einen imaginären Scheitelpunkt (Quelle), aus dem wir an jedem Scheitelpunkt des Graphen Kanten mit einem Gewicht von Null zeichnen. Jeder Zustand wird eindeutig durch den von der Quelle übergebenen Pfad bestimmt. Zusätzlich speichern wir die aufgewendete Zeit und die empfangene Freude.
Wir starten eine Prioritätswarteschlange mit einer festen Größe, in die wir den Status einfügen. Zur Beurteilung der Bedingungen in der Warteschlange verwenden wir das Verhältnis des empfangenen Glücks zur aufgewendeten Zeit. Diese Einschätzung ist nicht korrekt, hat aber bei dieser Aufgabe gute Ergebnisse gezeigt.
Bei jedem Schritt erhalten wir den Status mit der besten Schätzung aus der Warteschlange und stellen die daraus gebildeten Status in die Warteschlange. Bei diesem Ansatz wird es lange dauern, bis das endgültige Ergebnis erzielt wird.
Um die Lösung zu beschleunigen, werden wir Schritt für Schritt nach der Antwort suchen. Um bei jedem Schritt nach dem nächsten Scheitelpunkt im Pfad zu suchen, löschen wir die Warteschlange und platzieren den aktuellen Status darin. Dann werden wir eine feste Anzahl von Schritten ausführen und gleichzeitig den Zustand aktualisieren, der die größte Freude bereitet. Nehmen Sie als nächsten Scheitelpunkt des Pfades den Scheitelpunkt, der dem letzten Scheitelpunkt des aktuellen Zustands folgt, auf dem Pfad des resultierenden Zustands, der die größte Freude bereitet. Wir wiederholen die durchgeführten Aktionen, bis wir den aktuellen Status verbessern können.
Mögliche Verbesserungen
- Verwenden Sie die besten Heuristiken.
- Mit dieser Implementierung des Algorithmus werden zusätzliche Zustände angezeigt, da bei jedem Schritt alle Zustände hinzugefügt werden, die aus dem aktuellen stammen könnten. Um dies zu verhindern, können Sie mithilfe des Dijkstra-Algorithmus für jeden Scheitelpunkt des Diagramms zunächst einen Baum mit kürzesten Pfaden zu allen anderen Scheitelpunkten erstellen und Übergänge nicht in einem Schritt, sondern entlang des erstellten Baums vornehmen, bis wir die Scheitelpunkte erreichen, an denen wir noch nie waren.
Diese Änderungen ergaben keine signifikanten Verbesserungen, höchstwahrscheinlich aufgrund der Tatsache, dass es nur einen geschlossenen Test und keine Gruppe verschiedener generierter Tests gab.
Aufgabe I „Bärendigitalisierer“ (Alexander Samofalov)Schauen wir uns den
Quellcode des Dienstes an .
Eine Liste aller dem Benutzer zur Verfügung stehenden IDs finden Sie unter
/data .
Wenn es eine ID gibt, können die Daten unter Verwendung einer Anfrage an die Adresse
/data/id .
Für den Zugriff auf Daten benötigt der Dienst ein Token zur Authentifizierung. Wir haben ein verfügbares
Token , das jedoch abgelaufen ist und vom Dienst nicht mehr akzeptiert wird.
Lassen Sie uns im Code sehen,
wie diese Token generiert werden . Das Token wird erhalten, indem JSON der Form
{ “userId” : “id”, expireDate: “date”} und dann in base64 codiert wird. Der Dienst verwendet RSA zur Verschlüsselung, und der öffentliche Schlüssel kann auf Anfrage unter
/key abgerufen werden.
Stellen wir eine Anfrage: e = 30593, n = 66043. Seit Wenn n klein genug ist, können wir den privaten Schlüssel leicht berechnen.
Dazu zerlegen wir n in Primfaktoren: 211 * 313.
Wir berechnen
die Euler-Funktion von n: φ (n) = (211 - 1) (313 - 1) = 65520.
Wir erhalten d = e-1 (mod φ (n)) = 257.
Das inverse Element modulo kann mit dem
erweiterten euklidischen Algorithmus berechnet werden.
Nach der Berechnung des privaten Schlüssels entschlüsseln wir das uns zur Verfügung stehende Token.
Wir erhalten den folgenden JSON:
{"userId":"448f0a79-e2d8-4ccd-9009-53858914dcaa","expireDate":"2018-12-06T14:38:00.898026+00:00"}Beachten Sie
, dass der Dienst für den Benutzer mit der angegebenen Benutzer-ID ausreicht und expireDate kürzer als die aktuelle Zeit auf dem Server ist.
Wenn wir die Benutzer-ID kennen, können wir ein neues gültiges Token generieren.
Nehmen Sie dazu expireDate groß genug, um den Test zu bestehen - zum Beispiel
{"userId":"448f0a79-e2d8-4ccd-9009-53858914dcaa","expireDate":"2100-01-01T12:00:00.000000+00:00"} .
Wir verschlüsseln unser neues Token mit dem öffentlichen Schlüssel.
Nachdem wir eine Anfrage an
/data , stellen wir fest, dass der Benutzer Nachrichten mit Bezeichnern von 1 bis 4 erstellt hat.
Wir werden sie alle klären.
Unter ihnen ist ein wunderbarer Satz:
Neujahr klopft an die Tür, öffne sie bald! .
Tipps zur Lösung einiger anderer Probleme (von Artyom Romanov)Aufgabe A „Sicher mit Briefen“Möglicherweise stellen Sie fest, dass Sie alle zwanzig Schritte dieselbe Nummer erhalten.
Aufgabe B „Das Geheimnis des Professors“Sortieren Sie die Wörter in absteigender Reihenfolge der Beliebtheit. Möglicherweise stellen Sie fest, dass jedes nachfolgende Wort in ungefähr 2, 3, 4 usw. vorkommt. mal weniger als das beliebteste Wort. Jetzt können Sie die Antwort wiederherstellen.
Aufgabe C „Computerkatastrophe“Denken Sie an die Programmiersprache Whitespace.
Aufgabe J "Bengalen"Mögliche Platzierung:
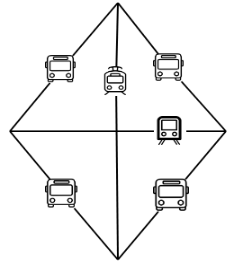
Problem K "Frosty Pattern"Um dieses Problem zu lösen, können Sie ein beliebiges geeignetes Dreieck auswählen, beispielsweise das richtige, und die Antwort darauf berechnen.
Danksagung
Der gesamte Prozess von der Idee bis zur Umsetzung wurde von Katya Lebedeva vorangetrieben und koordiniert. Katya Artamonova, Alina Mozhina, Sasha Komissarov und ich halfen ihr, die Aufgaben zu erledigen. Lyosha Tolstikov schrieb drei komplexe Prüfer, Sasha Komissarov und Seryozha Zherevchuk erstellten einen Server, Svyato und Seryozha erstellten selbstlos eine schöne Website mit enger Integration in Aufgaben: Jeder Teilnehmer konnte seinen Fortschritt und seine Rangliste sehen.