Erklärung der physikalischen Natur des Phänomens der "Auftriebskraft" ohne Verwendung der Bernoulli-Gleichung

Monin Ilya Alekseevich, Kandidat der MSTU für technische Wissenschaften, benannt nach Bauman., SM-9, imoninpgd@gmail.com

Kritik an der bestehenden theoretischen Erklärung des Auftriebs am Flügel eines Flugzeugs

Nachdem ich einen Vorlesungskurs am Moskauer Institut für Physik und Technologie, Fakultät für Aeromechanik und Flugzeugtechnik (FALT) „Einführung in die Aerodynamik“ gehört und mehrere verschiedene Universitätsstudenten über „Aerodynamik“ [1-3] gelesen hatte, war ich durch eine Reihe offensichtlicher Widersprüche in den Erklärungen der Physik der Strömung um eine Luft (Gas oder Ideal) verwirrt Flüssigkeiten) verschiedener fester Gegenstände und die Bildung von Auftrieb auf dem Flügel.

1. Die Hauptversion der vom Flügel auf den Flügel übertragenen Auftriebskraft beansprucht den Unterschied in den Geschwindigkeiten der Luftströmung (Flüssigkeit) über dem Flügel und unter dem Flügel, und infolgedessen entsteht ein Druckabfall gemäß dem Bernoulli-Gesetz. In diesem Fall ist nach dem Bernoulli-Gesetz die berechnete Strömungsgeschwindigkeit auf der Flügeloberfläche eindeutig mit dem instrumentell aufgezeichneten Druck auf den Flügel verbunden, wobei andere mögliche Erklärungen, die auf nicht weniger grundlegenden physikalischen Gesetzen beruhen, ignoriert werden.
2. Bei der Analyse der Strömungsprofile einer idealen nichtviskosen Flüssigkeit in ebenen Strömungen wurde im Vergleich zur Grundgeschwindigkeit V0 ein überraschend starker Anstieg der Strömungsraten erzielt. Das heißt, das Gesetz der Energieerhaltung wird widerlegt, da Energie aus dem Nichts entnommen wird, um die Strömung zu beschleunigen und die Energie der auf den Flügel einfallenden Strömung zu überschreiten. Gleichzeitig wird das Postulat der Hydrodynamik ignoriert, das nach dem gleichen Bernoulli-Gesetz, wenn der Strahl unter dem Niveau abläuft, den Geschwindigkeitskopf von oben durch den statischen Druck im Gefäß eindeutig begrenzt, d. H. Der Geschwindigkeitskopf des Strahls nach der Beschleunigung auf dem Flügel kann den beim Bremsen des Mediums komprimierten statischen Druck nicht überschreiten.

Für den Flug eines modernen Flugzeugs beträgt die erforderliche Hubkraft von 500-600 kg / m² Beim Starten und Landen beträgt die Geschwindigkeit moderner Flugzeuge etwa 250 km / h. In diesem Fall wird die notwendige Auftriebskraft auf den Flügel bei einer Strömungsgeschwindigkeit der oberen Ebene in der Größenordnung von 450 km / h bereitgestellt.

Was ist der Mechanismus einer solchen Beschleunigung des Luftstroms ohne sichtbaren Beschleunigungsmechanismus?

In der Tat kann der Kontakt des Flügels mit der entgegenkommenden Strömung nur zur Verzögerung der Strömung führen, nicht aber zu ihrer Beschleunigung!

Diese Widersprüche müssen beseitigt werden!

Die Physik darf ihre physikalische Bedeutung für schöne und komplexe mathematische Konstruktionen nicht verlieren!

Betrachten wir eine weitere Erklärung für die Bildung der Auftriebskraft des Flügels, ohne dass Verstöße gegen die Gesetze der Physik und des gesunden Menschenverstandes aufgedeckt werden. Dies erfordert die Anwendung der Gesetze der gewöhnlichen Mechanik.

In Anbetracht dessen betrachten wir, dass Luft aus einzelnen Partikeln (die sich gegenseitig abstoßen (um Gasdruck zu erzeugen)) mit ihrer eigenen Masse besteht, von denen jedes den Gesetzen der Mechanik folgt, wenn seine Richtung und Geschwindigkeit geändert werden.

Die Mehrdeutigkeit des Verhältnisses der Verdünnung über dem Flügel mit einer erhöhten Durchflussrate

Der betrachtete reale Flügel ist kein Element einer idealen Röhre im Bernoulli-Gesetz-Modell, sondern ein begrenztes festes Objekt in einem unbegrenzten Raum eines sich bewegenden realen Gases, das aus Gaspartikeln besteht, die in Masse und Größe ziemlich greifbar sind. In diesem Fall sollte man die gekrümmte Strömung von Düsen über die gekrümmte Oberfläche des Flügels berücksichtigen und dabei die Trägheitskräfte und den erzeugten Druck senkrecht zum Geschwindigkeitsvektor und zur Oberfläche des Flügels berücksichtigen.

Wenn wir die Bewegung der Düsen über das Flügelprofil betrachten, kann ein Luftstrom aufgrund der Krümmung seiner Strömung ein Vakuum über dem Flügel erzeugen.

Um die geradlinige Bewegung des Körpers zu biegen, müssen Sie eine Kraft in der Richtung senkrecht zum Geschwindigkeitsvektor aufbringen. Bei einem kontinuierlichen ebenen Strom ist es aufgrund seiner Krümmung erforderlich, die Druckdifferenz darüber und darunter sicherzustellen. Gleichzeitig wird der Druck auf der konvexen Seite des Strahls erhöht und der Druck auf der konkaven Seite verringert.
Wenn Sie sich um den Umfang eines Materialpunkts bewegen, wird die zentripetale Beschleunigung durch Kraft erzeugt

F = m * V ^ 2 / R.

Und bei gleicher Kreisbewegung einer dünnen Gasschicht mit der Dicke dR ist die Masse gleich

m = q * S * dR ,

wobei S die Fläche der Gasschicht ist, q die Dichte des Gases ist. Wenn Sie die Zentripetalkraft auf den Elementarbereich der Gasschicht bringen, wird die Kraft in Druck umgewandelt

P = q * V ^ 2 * dR / R.

Wenn ein Luftstrom über die Flügeloberfläche strömt, bewegt sich die Gasschicht entlang eines gekrümmten Pfades. Jeder Punkt dieser Trajektorie hat einen eigenen Krümmungsradius, mit dem wir den Trägheitsgasdruck in der Richtung senkrecht zur Geschwindigkeit berechnen können.

Somit ist es möglich, den Druck (Vakuum) auf den Flügel direkt aus der über seiner Oberfläche strömenden Gasschicht zu berechnen, und es wird immer angenommen, dass die Gasströmungsgeschwindigkeit gleich der Flügelgeschwindigkeit Vo ist.

Zunächst betrachten wir den einfachsten Fall eines Flügels in Form einer Platte mit einer Dicke von Null, die mit einem Radius R gebogen ist. Solche dünnen gekrümmten Profile werden für ultraleichte Segelflugzeuge bei der Flugzeugmodellierung verwendet.

Übrigens sollte nach der üblichen Theorie des Bernoulli-Gesetzes eine dünne gekrümmte Platte überhaupt keine Auftriebskraft haben, da die Weglänge unter dem Flügel und über dem Flügel gleich ist. Aber der dünne Flügel hat Auftrieb und ist sehr bedeutsam, was die Unrichtigkeit des Auftriebsmodells unter Verwendung des Bernoulli-Gesetzes deutlich zeigt.

Für die geschätzte Berechnung des Flügels wählen wir die für Flugzeuge mit niedriger Geschwindigkeit übliche Profilhöhe von 20% der Flügelbreite. In diesem Fall nehmen wir für die Höhe des Profils den Höhenunterschied zwischen Vorder- und Hinterkante in Bezug auf den horizontalen Luftstrom (siehe Abb. 1-3).


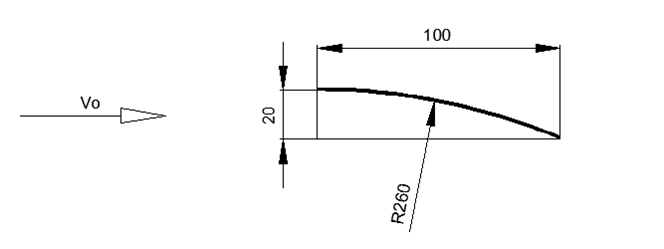Abb. 1. Dünne Flügelgeometrie mit konstanter Krümmung


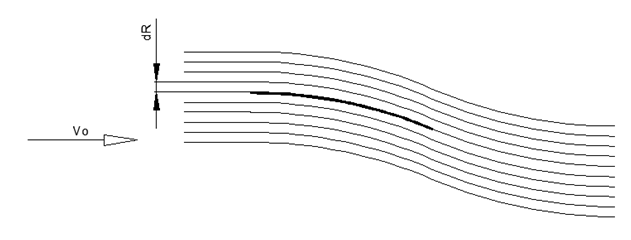Abb. 2. Geschätzte Strömung um einen Flügel mit dünnem Radius


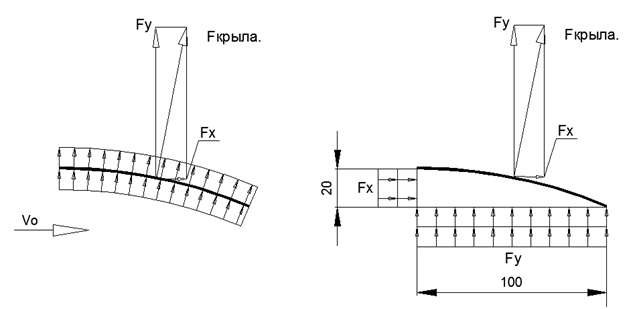Abb. 3. Die Art der Druckverteilung über einen Flügel mit dünnem Radius und die resultierenden Kräfte in den Richtungen

Bei einer Breite von 1 m und einer Höhe von 20% des Profils beträgt der Flügelradius 2,6 m, vorausgesetzt, die Tangente an den Flügel ist oben am Profil horizontal.

Nun berechnen wir den Zentripetaldruck auf den Flügel aus der entlang des Bogens gekrümmten Luftschicht.

Bei einer Geschwindigkeit von 70 m / s (252 km / h) beträgt der Druck einer Schicht mit einer Dicke von 0,1 m und einem Krümmungsradius von 2,6 m 235,6 Pa oder 24 kg / m², und der Wert der Geschwindigkeitskopfhöhe bei 70 m / s beträgt 3063 Pa.

Da ein dünner Flügel von zwei Seiten herumfließt, müssen diese Werte mindestens verdoppelt und dann mit einer bestimmten Anzahl paralleler Schichten multipliziert werden, die ebenfalls vom sich bewegenden Flügel gekrümmt werden. Wenn wir annehmen, dass die Dicke der gestörten Schicht nicht weniger als die Hälfte der Breite des Flügels auf jeder Seite des Flügels beträgt, erhalten wir die zehnfache Gesamtbelastung des Flügels von etwa 2356 Pa. Diese Zahlen übertreffen die Flügellastwerte für langsame Leichtmotorflugzeuge mit einem dicken Flügel und einer ähnlichen Krümmung der Flügeloberfläche. (siehe Tabelle 1)

Da der Druck Pcr auf die gekrümmte Oberfläche der dünnen Platte ausgeübt wird, kann die Kraft Fcr von Pcr in die Auftriebskraft Fy und den Widerstand gegen Flug Fx zerlegt werden.
Die Auftriebskraft Fy ist gleich dem Integral der Projektion auf die Y-Achse der Kräfte aus dem Druck der krummlinigen Strömung Pcr über die gesamte Fläche des Flügels.

Bei gleichmäßigem Druck auf den kreisförmigen Flügel ist der Wert von Fy gleich dem Produkt Pcr durch die Projektionsfläche des Flügels durch die X-Achse, was gleich S = B * L des Flügels ist (in diesem Fall 1 m² / mp).

Fy = Pkr * Bkr = 2356 * 1 = 2356 N / Fp.

Gleichzeitig ist der Widerstand gegen horizontale Bewegung in diesem Fall gleich dem Projektionsintegral dFcr auf der X-Achse über die gesamte Flügelfläche. Bei gleichmäßigem Druck auf den Flügel ist der Wert von Fx gleich dem Produkt Pcr durch die Projektionsfläche des Flügels auf der Y-Achse, die gleich der Höhe H des Flügelprofils ist (in diesem Fall 0,2 m² / mp).

Fx = Pkr * Nkr = 2356 * 0,2 = 462 N / Fp.

In diesem Fall erhalten wir K = Fy / Fx = (Pkr * Vkr) / (Pkr * Nkr) = Bkr / Nkr, dh bei gleichmäßigem Druck auf ein kreisförmiges dünnes Profil ist die Qualität des Flügels gleich dem Verhältnis nur der geometrischen Parameter des Profils K = B / N.

Nach der Regel der Vektorexpansion von Kräften aus einem gegebenen Bild können Sie sofort den Wert der Qualität des Flügels K = Fy / Fx erhalten, der in diesem Fall gleich K = 100 * Pkr / 20 * Pkr = 5 ist.

Es ist interessant, dass der Druck auf den Flügel bei gleichen Fluggeschwindigkeiten unverändert bleibt, wenn Sie diesen Konstruktionsflügel auf eine zehnfache Abnahme skalieren (entlang des Krümmungsradius, der Höhe und Breite des Profils) (siehe Tabelle 2). Aus diesem Grund fliegen schwere Marschflugkörper auf eher kleinen, dünnen Flügeln. Es stellt sich heraus, dass ihre kleinen und dünnen Flügel mit ausreichender Krümmung wirklich ausreichen, um die notwendige Hubkraft zu erzeugen!

Da die Modellierung von Räumen billig genug ist, werden diese Zahlen bei Modellen in Originalgröße ganz einfach überprüft.

Tab. 1. Der Druck gekrümmter Luftschichten auf einen Flügel mit konstantem Radius R = 2,6 m, abhängig von der Fluggeschwindigkeit.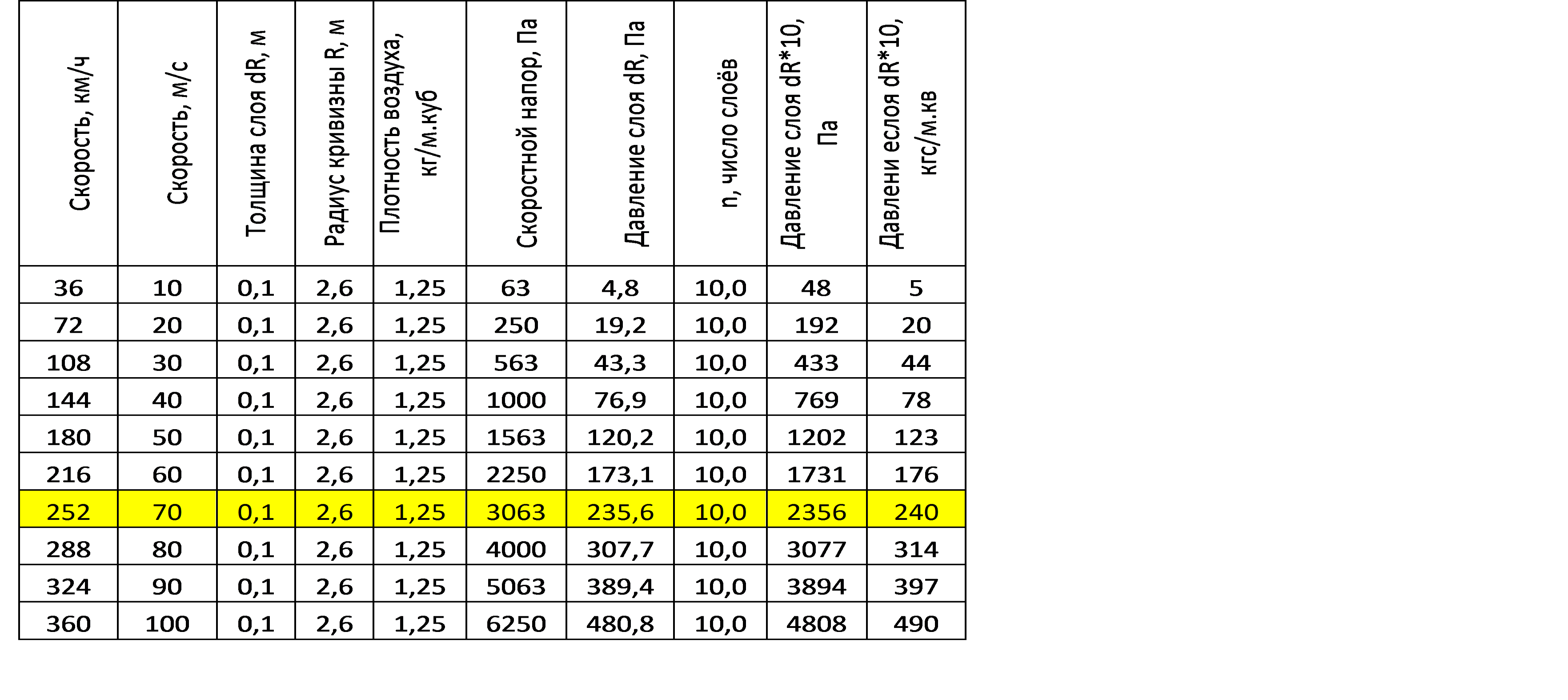



Tab. 2. Der Druck der gekrümmten Luftschichten auf den Flügel mit konstantem Radius R = 0,26 m, abhängig von der Fluggeschwindigkeit.



Es ist interessant zu betrachten, wie sich der Flügel Kkr mit seiner konstanten Krümmung Rkr ändert, jedoch mit einem sich ändernden Profilbreitenparameter Vkr. (Siehe Tabelle 3)

In der allerersten Zeile der Tabelle erreicht die aerodynamische Qualität des Flügels einen fantastischen Wert von K = 182, aber die Belastung des Flügels beträgt nur 67 Pa (7 kgf / m.sq.), was nur für Flugzeugmodelle von Segelflugzeugen mit Raumabmessung geeignet ist.

Die notwendige Hubkraft auf den Flügel entsteht nur bei ausreichend kleinen K-Flügeln, die aus den letzten Zeilen des Tisches ersichtlich sind.

Die Spalte des Variablenparameters und die Zeile des Anfangsprofils mit Kkr = 5 sind gelb hervorgehoben.

Tab. 3. Ändern der Parameter eines Flügels mit konstantem Radius R = 2,6 m bei verschiedenen Profilwinkeln (Profilbreite) bei konstanter Fluggeschwindigkeit.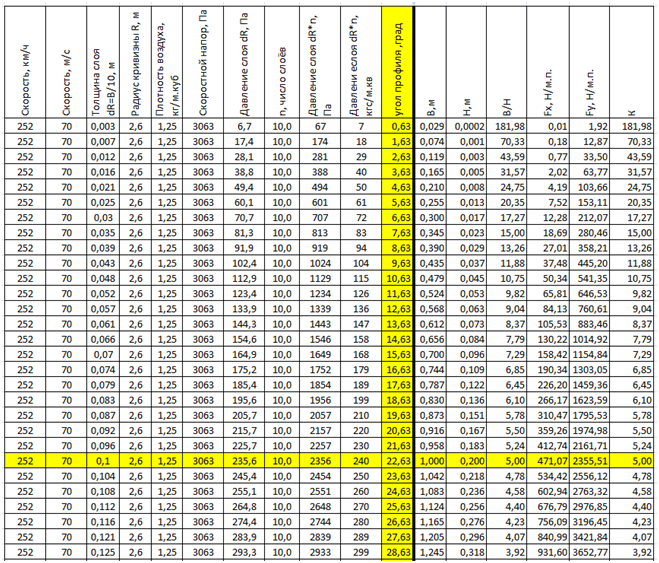



Sie können auch die Änderung der Auftriebskraft Fy und die Qualität des Flügels Kkr für den Flügel mit einer konstanten Sehne, jedoch mit unterschiedlicher Krümmung des Flügels bei konstanter Geschwindigkeit berechnen. Die gelb hervorgehobenen Spalten sind: Variables Argument Rcr - Krümmungsradius und konstante Profilbreite Vcr. Die Zeile des Anfangsprofils mit Kkr = 5 wird ebenfalls hervorgehoben.

Tab. 4. Ändern der Parameter eines Flügels mit variablem Krümmungsradius bei konstanter Profilbreite B = 1 m bei konstanter Fluggeschwindigkeit.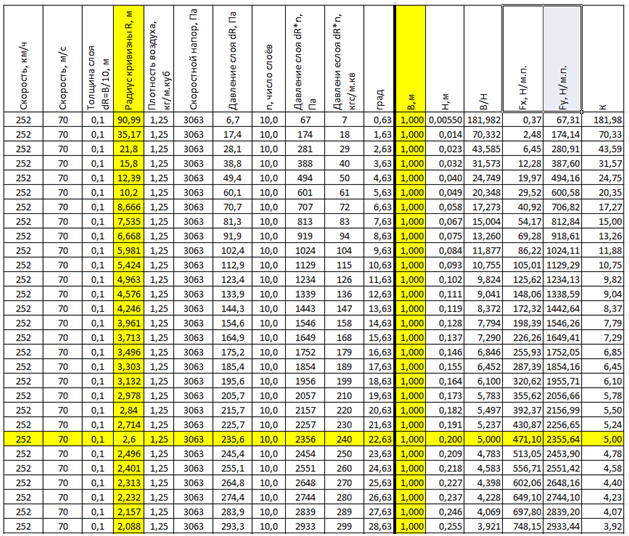



In dem beschriebenen Modell ist keine zusätzliche Beschleunigung der Luft über dem Flügel erforderlich, um ein Vakuum über dem Flügel zu erhalten. Eine spürbare Entladung über dem Flügel ist unter Bedingungen einer signifikanten Krümmung des Luftstroms um den Flügel unter dem Einfluss statischer Luftdruckkräfte des gesamten umgebenden Raums gewährleistet. Der Neigungswinkel der Sehne der anfänglich gekrümmten Platte beträgt 11,3 Grad (der halbe Winkel des Bogensegments beträgt 22,6 Grad), was gut mit den Landemodi des Flügels moderner Flugzeuge während der Landung bei losgelassener Flügelmechanisierung (Lamellen + Klappen) übereinstimmt. Im Landemodus erinnert der Flügel mit der freigegebenen Mechanisierung viel mehr an den betrachteten Fall einer gekrümmten dünnen Platte als der klassische Flügel mit einer geraden unteren Ebene (siehe Abbildung 4).



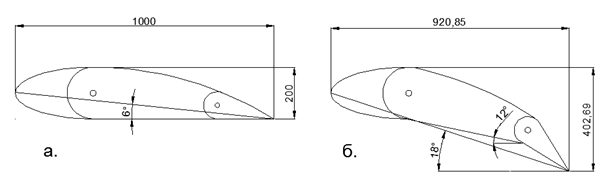Abb. 4. Asymmetrischer Flügel mit einer flachen unteren stromlinienförmigen Oberfläche: a) eine gerade Position für Hochgeschwindigkeitsflüge; b) Flügel mit maximaler Krümmung bei vollständig freigegebener Mechanisierung.

Der stark gekrümmte dünne Flügel wird häufig als Lüfterflügel verwendet. Niedrige lineare Drehzahlen bei niedrigen Druckwerten ermöglichen die Verwendung von dünnen Stahl- oder Kunststoffplatten mit extrem geringer Dicke als Lüfter in den Lüftern, da ihre Festigkeit ausreicht, um den vorhandenen Belastungen standzuhalten.

In schweren Flugzeugen ist die Verwendung dünner Flügel aufgrund ihrer unzureichenden Festigkeit technisch unmöglich. Die große Dicke des Flügels ermöglicht es Ihnen, innerhalb des Flügels ziemlich hohe tragende Träger mit ausreichender Festigkeit und Steifigkeit zum Biegen und Torsion zu platzieren, während Sie ein akzeptables Gewicht für das Flugzeug beibehalten. Aus diesem Grund untersucht jede Aerodynamik Flügel mit einer ziemlich greifbaren Dicke. Aus diesem Grund bewegen wir uns von der Betrachtung der Aerodynamik einer dünnen gekrümmten Platte zum Flügelprofil mit realer Dicke und Ebenen unterschiedlicher Krümmungen.

Am Ende der Betrachtung des Strömungsmodells um einen dünnen Flügel muss ein weiterer Beweis für die Funktionsfähigkeit des vorgeschlagenen Modells zur Erklärung der „Auftriebskraft des Flügels“ erbracht werden. Wie aus der Mechanik bekannt ist, ist Stärke die Änderung des Impulses pro Zeiteinheit, d.h.

F = d (m · V) / dT

Im stimmhaften Modell der Strömung um einen dünnen gekrümmten Flügel können wir die Auftriebskraft Fy als vertikale Änderung des Impulses der einströmenden Luftströmung berechnen, die als betrachtet wird

Fy2 = (dR * 10 * q * Vo) * Vo * sinAcr ,

Dabei ist Vo die Flügelgeschwindigkeit, dR die Dicke der elementar gekrümmten Schicht des Luftstroms im Berechnungsmodell, 10 die Anzahl der gleichzeitig zu krümmenden Schichten und Acr der Abstiegswinkel der Strömung vom Flügel zur Richtung der Anfangsgeschwindigkeit Vo.

Nachdem wir die Berechnung durchgeführt haben, erhalten wir, dass beide Berechnungen das gleiche Ergebnis liefern.

Oder in analytischer Form:

Fy1 = Pcr * Bcr ,

Pkr = (dR * 10 * q * Vo) * Vo / R ,

Bcr = R * sinAcr

Wenn wir die Entwicklung Pkr und Bkr im Ausdruck für Fy1 einsetzen und den gleichen Namen R im Zähler und Nenner reduzieren, erhalten wir:

Fy = Pkr * Bkr = (dR * 10 * q * Vo) * Vo * sinAcr

Die Gleichheit Fy = Fy1 = Fy2 ist also immer wahr

Das heißt, die "Inertial-Curvilinear" -Methode zur Berechnung der "Auftriebskraft" eines Flügels ergibt eine Formel, die mit der "Reactive-Pulse Force" -Methode für einen Flügel derselben Geometrie identisch ist.
Dies bedeutet, dass Flugzeuge nicht aufgrund einer Art „magischer“ Kraft aus „magischen Wirbeln“ fliegen, sondern aufgrund des alten und verständlichen „Impulses der Kraft“ oder des „Jet-Schubes“ beim Abwerfen einer Luftmasse.

Fetter Flügel

Bei niedrigen Fluggeschwindigkeiten während des Starts und der Landung (M = 0,2 oder 250 km / h) überschreitet die Druckhöhe 3 kPa (3% des atmosphärischen Drucks auf Meereshöhe von 100 kPa) nicht, dh sie ist im Verhältnis zum atmosphärischen Grunddruck so gering, dass Die geometrische Kompression der Strömung wird visuell nicht mehr nachweisbar, wenn ein Strahl in der Nähe des Flügels gezogen wird.

Um einen Auftrieb über dem Flügel zu erzeugen, muss eine Krümmung der Strömung erzeugt werden, so dass sich der Flügel in der konkaven Zone der Luftströmung befindet. Um eine solche Krümmung des Strahls über dem Flügel sicherzustellen, hilft die Krümmung der oberen Ebene des Flügels, die sich im aerodynamischen Schatten der Nasenverkleidung des Flügels befindet.

Gleichzeitig fließt die untere Ebene des Flügels entweder in einer geraden Linie, ohne ein Vakuum zu erzeugen, oder auf einer konkaven Oberfläche, wobei der Luftstrom nach unten verworfen wird, was einen positiven Druckanstieg auf den Flügel von unten erzeugt und mit der Auftriebskraft aus dem Vakuum über dem Flügel kombiniert wird.
Der Hauptunterschied zwischen einem dicken Flügel und einer dünnen Platte in unserem Fall ist das Auftreten einer Frontverkleidung, die den entgegenkommenden Luftstrom verteilt, bevor er gekrümmte Ebenen erreicht, die Auftrieb erzeugen.

Vor dem fliegenden dicken Flügel entsteht eine Bremszone, in der die Luftgeschwindigkeit gleich Null (relativ zum Flügel) wird und der Überdruck in dieser Zone gleich dem Druckkopf Pvo ist.

Es wird nicht möglich sein, Stromlinien zu zeichnen, ohne die Luftkompression zu berücksichtigen, andernfalls muss man entweder die Version der Luftbeschleunigung über der Flügeloberfläche akzeptieren oder die Einflusszone mit einer Strömungskurve wird in einem inkompressiblen Medium ins Unendliche rasen, was unplausibel ist.
Übrigens manifestieren sich beide Effekte (Beschleunigung der Strömung und unendliche Einflusszone in inkompressiblen Flüssigkeiten) in der Praxis in Windkanälen mit Rauchströmungslinien und wenn sich die U-Boote in geringen Tiefen bewegen.

In Windkanälen (ADT) erfolgt die Strömung um die getesteten Modelle mit einer spürbaren Beschleunigung der Strömung (Verringerung der Dicke der Rauchleitungen) im Wandspalt des ADT-Modells. Das ist nur die Interpretation dieses Phänomens wird völlig fälschlicherweise auf die Beschleunigung der Strömung zur Bildung der Hubkraft zurückgeführt. Tatsächlich ist die Beschleunigung der Strömung in der Lücke „ADT-Modellwand“ einfach eine Folge der Verengung der Bohrung im ADT-Strömungsweg, während ein konstanter Luftstrom im ADT selbst aufgrund leistungsstarker Lüfter mit einer steifen Lüftercharakteristik aufrechterhalten wird.

Wenn sich die U-Boote in geringen Tiefen über dem U-Boot bewegen, bildet sich ein visuell wahrnehmbarer Wasserbuckel. Der Wert dieses Buckels entspricht dem Wasservolumen vor dem Rumpf des U-Bootes, das bei einer bestimmten Geschwindigkeit von der Zone vor dem U-Boot in die Heckzone bewegt werden muss. Ein Buckel auf der Oberfläche entsteht auch, wenn sich das U-Boot in großen Tiefen bewegt. Aufgrund des größeren Ausbreitungsbereichs des Buckels wird seine Höhe jedoch durch einfache visuelle Beobachtung nicht mehr nachweisbar. Die Ursache für den Wasserhöcker auf der Oberfläche erklärt sich aus der Unfähigkeit, die inkompressible Flüssigkeit nach unten zu bewegen, und nach oben wird eine dünne Wasserschicht unter atmosphärischem Luftdruck leicht vorgespannt, mit einer deutlichen elastischen Eigenschaft der Quelle von atmosphärischem Druck und Schwerkraft. Übrigens kann selbst bei der Bewegung von U-Booten in großen Tiefen ein Wasserbuckel (und damit das U-Boot selbst) durch Beobachtung von Satelliten mit hochempfindlichen Geräten erfasst werden, die die Oberflächengeometrie der Meere mit großer Genauigkeit messen und den Wasserbuckel des U-Bootes vom Rauschen der Wellen auf der Oberfläche mit isolieren können mit Computern.

Wir nehmen also an, dass das Gas komprimierbar ist, und stellen die Einflusszone von der Flügelhülle so ein, dass sie vom Kompressionsverhältnis des Strahls zum Druck Pvo abhängt.

Der Druck in der Bremszone an der Verkleidung wird durch gekrümmte Luftstrahlen gehalten, die die Verkleidung umhüllen. Das Druckverhältnis zur Krümmung der Luftschichten ist das gleiche wie im Fall eines dünnen gekrümmten Flügels dP = q * Vo ^ 2 * dR / Rsl.

Die Größe der Einflusszone, in der die Krümmung der Strömung spürbar ist, hängt auch mit der Größe von Vkr und Nkr zusammen.Der Druckanstieg vor der Verkleidung wird durch den Druckabfall im Satellitenstrom hinter dem Flügel kompensiert, d. H. Der Flügel bildet einen linearen Druckdipol, der in großer Entfernung den umgebenden Luftraum bei niedrigen (Unterschall-) Fluggeschwindigkeiten praktisch nicht mehr beeinflusst.

Wenn Sie die Form der Nasenverkleidung annehmen, entspricht die halbe Höhe des Profils Nkr / 2 = Rlob.

Wir glauben, dass die Bremszone mit dem Druck vo vollständig durch die Krümmung der Schicht innerhalb der Grenzen der Profilbreite erzeugt wird, dann können wir den Krümmungsradius des Strahls mit einer Dicke / 2 = Rlob abschätzen.
Es ist notwendig, die Bedingung Pr = Pvo zu erfüllen.

Daher ist

qVo ^ 2 * Rlob / R = qVo ^ 2/2.

Nach Reduzierung der gleichen Dichte- und Geschwindigkeitsterme auf der linken und rechten Seite der Gleichung erhalten wir

R = 2 * Rlob

Es stellt sich also heraus, dass die Grenzkrümmungsradien der einströmenden Strömung ausschließlich durch die Krümmung der Verkleidung (lokale Profilhöhe) begrenzt sind und gleichzeitig unabhängig von der Geschwindigkeit sind.

Wenn sich der einfallende Strahl dreht, um das Profil zu umgehen, tritt unvermeidlich eine Situation auf, in der die Strahlgrenze mit der Nulldurchflusslinie die Verkleidung berührt. An diesem Tangentialpunkt wird die Strömungsgeschwindigkeit vom Flügel weg gerichtet und die Strömungskurve erreicht den Wendepunkt. Das heißt, an diesem Punkt trennt sich die Schicht mit einer Änderung der Konvexitätsrichtung der Strahlkrümmung vom Flügel (siehe Fig. 5).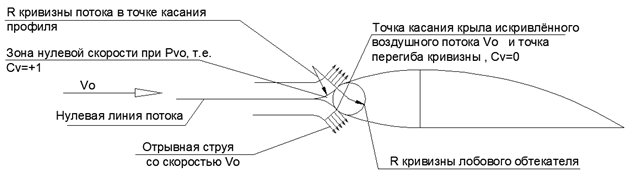



Abb. 5. Das Zusammenspiel des freien Flusses Vo mit der Frontverkleidung.

Bei hohen Fluggeschwindigkeiten ist der Geschwindigkeitskopf Pvo so groß, dass sich der Strahl von der Nasenverkleidung löst und, nachdem er einen langen Bogen über der Flügelebene beschrieben hat, zur Flügeloberfläche zurückkehrt.

An der Stelle, an der der zerrissene Strahl zur Flügelebene zurückkehrt, tritt ein Aufprall auf, und der Strahl ändert abrupt die Richtung zur Tangente an die Flügelebene. In diesem Fall entsteht unter dem Lichtbogen eines fliegenden Strahls vom Trennpunkt zum Rücklaufpunkt ein geschlossener Niederdruckhohlraum. (siehe Abb. 6).

In der traditionellen „Bernoulli-Aerodynamik“ wird die beschriebene Bildung einer entwickelten abgetrennten Blase mit starker Entladung und die Stoßrückführung des abgetrennten Stroms wie folgt erklärt: „... Bei hohen Überschall- und Transsonikgeschwindigkeiten beschleunigt sich der Luftstrom über dem Flügel auf Überschallwerte, wodurch der Druck über dem Flügel erheblich abnimmt dann entsteht ein Druckstoß (Auswirkung des Übergangs zum Überschall), mit dem Übergang danach zu einem Unterschallstrom ... “ Eine solche Erklärung scheint eine klare Strecke realer experimenteller Daten zu einer unhaltbaren Theorie zu sein.

Da die Verkleidung die einfallende Strömung entlang der Nulllinie in zwei Teile teilt, erfolgt eine Strömungstrennung auf beiden Flügelebenen. Aufgrund der unterschiedlichen Richtungen der Ebenen in Bezug auf die Strömung (auf die Strömung oder im aerodynamischen Schatten) haben die abnehmbaren Entladungsblasen über und unter dem Flügel unterschiedliche Größen, und die Aufprallkraft des Rückstrahls ändert sich auch proportional zur Größe der Ablösungsblase.

Auf der Grundlage einer solchen Verteilung der Druckkurven auf der Frontflügelverkleidung und der erhaltenen Kcr-Eigenschaften von Flügelplatten mit dünnem Radius in Abhängigkeit von der relativen Dicke des Vkr / Nkr-Profils. Es ist leicht zu verstehen, welche Ursachen und Muster ein solches Phänomen wie die „Straffung“ verschiedener geometrischer Formen aufweist (siehe Diagramm Cx in Abb. 6).

Es wäre auch äußerst interessant, Druckdiagramme während der Strömung um axialsymmetrische Standardkörper durch Strahlströmungen zu betrachten und ihre Cx- und Cd-Hüllkurven über Abschnitte und nicht nur einen Gesamt-Cx-Koeffizienten für die gesamte Figur zu erhalten.



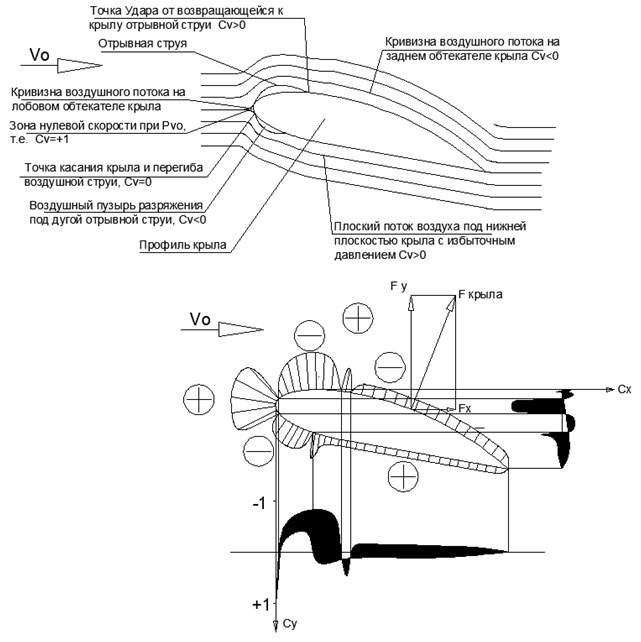Abb. 6. Luftstrom um einen dicken Flügel mit ausgeprägten charakteristischen Bewegungselementen. Diagramm der Flügeldrücke und Diagramme des Druckkoeffizienten Su entlang der Flügelsehne und Cx entlang der Flügelhöhe. Die Fläche der schattierten Bereiche entspricht den Gesamtkräften in den Richtungen Y bzw. X.

Bei niedrigen M-Zahlen wird die Haupthebekraft im Bereich der Nasenverkleidung in den abnehmbaren Blasen gebildet. Bei einer kleinen Anzahl von M geht der Rückstrahl in der Trennzone tangential zum dicken Profil des Flügels und verursacht am Rücklaufpunkt keinen Aufprall. Wenn sie sich jedoch M = 1 nähern, blasen sich die Trennblasen so stark auf, dass es unmöglich wird, die gewünschte Profildicke für den kontinuierlichen Fluss des Strahls zu erreichen, und dann kommt es zu einer ausgeprägten Trennung des Flusses mit der Bildung der separaten Blase, die visuell anhand der Schwingungen der auf die Flügelebene geklebten Seidenmasken beobachtet wird. Das Aufblasen von Trennblasen in der Höhe wird zu einem Hindernis für den Geschwindigkeitsgewinn, und daher beginnt ihre Entwicklung aufgrund des Schärfens der Nasenkante (Verringerung des Radius der Frontalverkleidung) verringert zu werden.
Bei transsonischen Fluggeschwindigkeiten erreicht die hintere Grenze der Trennblase die Hinterkante des Flügels, wonach die Volumina der oberen Trennblase mit der Hochdruckzone der unteren Ebene des Flügels verbunden werden. In den kombinierten Volumina der oberen und unteren Trennblasen wird der Druck ausgeglichen und die Auftriebskraft des Flügels Fy fällt stark ab.

Während des Überschallfluges wird der Flügel mit der üblichen Tropfenform völlig unanwendbar, und stattdessen erscheint ein Flügel mit einem entwickelten scharfen "Schnabel", auf dem nun der Hauptteil der Auftriebskraft erzeugt wird, während die Möglichkeit einer Abreißblase minimiert wird.

Um die Landeflugbedingungen bei niedrigen Machzahlen zu gewährleisten, ist im Flügel mit „dünner Rechnung“ eine auslenkbare Mechanisierung vorne und hinten installiert (siehe Abb. 7). Diese Art von dünnen Flügeln mit scharfen Vorderkanten und abgelenkter Mechanisierung vorne und hinten wird Kampfkämpfern von 4-5 Generationen ausgesetzt (siehe Foto 1-2). Wenn die Mechanisierung nach unten abweicht, nähert sich der „dünn gebogene“ Flügel den Fließeigenschaften einer dünnen gekrümmten Platte an, was das Starten und Landen bei niedrigen Geschwindigkeiten und mit einem kurzen Lauf entlang der Landebahn ermöglicht. In Zukunft ist es möglich, bei Manövern mit niedrigen Geschwindigkeiten vollständig auf das Drehen des Flügelflugzeugs umzuschalten, wie dies bereits bei einer voll drehbaren Heckeinheit von Jägern der Fall war.Eine vollständig rotierende Flügelebene ermöglicht es, ein starkes Ausbeulen des Rumpfes gegen den Luftstrom zu vermeiden und die Gleichrichtung des Schubvektors der Triebwerke zur Fluggeschwindigkeit bei großen Anstellwinkeln aufrechtzuerhalten.



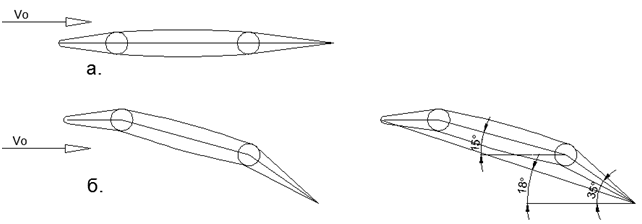.7. /=0,1 (10%) «» : ) ; ) .



.1. - 35 ( ).



.2. -29 - ( ).



.3. -29 .

Auf dem Foto (siehe Foto 3) ist die Form der „scharf gebogenen“ Lamelle im Schnitt deutlich sichtbar: eine flache Unterseite und eine radiale Oberseite. Die Vorderkante selbst ist keineswegs scharf, sondern hat einen sehr spezifischen kleinen Radius, wodurch die Aerodynamik des Unterschallfluges verbessert wird. Die Steuerung der Steigungsneigung zur entgegenkommenden Strömung ermöglicht die Optimierung der Art der Bildung der Trennblase bei niedrigen Geschwindigkeiten, wodurch Bedingungen für ihren kontinuierlichen Zusammenbruch geschaffen werden. Unter Berücksichtigung der Kunstflugkunst mit der Möglichkeit eines langen Fluges auf dem Kopf können Sie mit der nach oben gekippten Lamelle die Durchbiegung eines flachen, dünnen Flügels umkehren, um einen vollständig effektiven Flug in einer auf dem Kopf stehenden Position zu erzielen, obwohl die Aerodynamik schlechter ist als in einer normalen Position. Bei späteren Su-35- und Su-57-Flugzeugen ist die Vorderkante schärfer und symmetrischer keilförmig.da es für einen längeren Überschallflug ausgelegt ist.

Vortex und Vortex Drag

Im Netzwerk finden Sie viele Erklärungen zu jedem Thema, einschließlich der Wirbelbildung am Flügel eines Flugzeugs, zum Beispiel:



Gleichzeitig ist es leicht, Fotos von Wirbelspuren von Flugzeugen in Wolkenschichten im selben Internet zu finden, die ein viel größeres Ausmaß des Phänomens zeigen, als sie theoretisch zu zeigen versuchen.



Foto 4. Wirbelspur in einer Nebelschicht hinter einem Flugzeug, das in einer Höhe fliegt. Die Ringe des sichtbaren nebligen Wirbelwinds sind Hunderte von Metern vom Flugzeug entfernt, und die visuelle Nähe ist eine optische Täuschung, die von einem Teleobjektiv erzeugt wird, wenn ein Flugzeug aus einer Entfernung von mehreren Kilometern aufgenommen wird.



Foto 5. Wirbelspur in einer Nebelschicht hinter einem Flugzeug, das in einer Höhe fliegt. Sichtbar ist ein vertikaler Luftstrom und Luftwellen, die von den Seiten hereinkommen und zu einer Spirale verdreht sind, die mit einem vertikalen Abwärtsstrom in Kontakt steht.



Foto 6. Wirbelspur in einer Nebelschicht über einer Landebahn hinter einem Landeflugzeug.

Diese riesigen Wirbelwinde hinter den Flugzeugen entstehen aufgrund der Endwirbel am Flügel überhaupt nicht. Natürlich gibt es Endwirbel, aber ihre Rolle ist nicht so groß, und Flugzeugkonstrukteure kämpfen aktiv und erfolgreich damit.

Großflächige Wirbel aus Fotografien bilden sich weit hinter dem Flugzeug, wenn eine vom Flugzeug herabgeworfene Luftwelle auf zwei Seiten durch den Luftstrom unter der absteigenden Schicht von oben in den verdünnten Raum ersetzt wird (siehe Foto 4-5). Diese Erklärung der Bildung des Satellitenwirbels spiegelt das bereits betrachtete Problem der „Einflusszone des Flügels auf den umgebenden Raum“ wider. In diesem Fall liegt die Rolle der Erdoberfläche in der Grenze der Verteilung des Abwärtsstroms der Luft, die vom Flügel nach unten geworfen wird. Das heißt, der Flug des Flugzeugs und die Erzeugung einer „Auftriebskraft des Flügels“ ist auch ohne feste darunter liegende Oberflächen möglich. Gleichzeitig bewegt sich der nach unten geworfene Luftstrom unendlich lange nach unten und verliert Geschwindigkeit und kinetische Energie, wenn er sich wegbewegt, wobei der vertikale Impuls unverändert bleibt. Die kinetische Energie der anfänglich verworfenen Luftmasse geht verloren, wenn seitliche Luftströme in die Bewegung einbezogen werden, deren symmetrische Multidirektionalität den vom Flugzeugflügel erzeugten anfänglichen Gesamtimpuls nicht ändert. Ein klares Beispiel für die Rolle des Erdbegrenzers ist Foto 6. Dort fällt der geradlinige Nebelstrom über dem Landeflugbus (siehe Foto 6) geradlinig auf den Boden ab, und erst dann beginnt weit hinter dem Flugzeug eine seitliche Verschiebung entlang des Bodenbegrenzers, und Nebelschichten von den Seiten und von oben nähern sich bereits in der Mitte der Satellitenschicht und drehen sich ein doppelte selbstkompensierende Spirale um die Abwärtsströmung.

"Screen Effect" beim Fliegen eines Flügels in der Nähe der Erde

Angesichts der angegebenen Rolle der Erde bei der Bildung der „Auftriebskraft des Flügels“ ist es sinnvoll, zusätzlich den „Screen-Effekt“ zu berücksichtigen, der ohne das Vorhandensein einer festen Erdoberfläche nicht auftreten kann. Daher hat die Physik des Flügelfluges im endlosen Luftraum und auf dem „Bildschirmeffekt“ in der Nähe der Erde eine ganz andere Natur.

Erklärungen des Ekranoplan-Effekts basierend auf der Gaskompressibilität bei niedrigen Mach-Zahlen

Die Auswirkung einer eng beieinander liegenden Erdoberfläche auf den Auftrieb eines Flügels wird als "Bildschirmeffekt" bezeichnet. Mit diesem Effekt steigt die Auftriebskraft des Flügels stark an, wenn in der Nähe einer festen Oberfläche (Erde, Wasser) in einer Höhe geflogen wird, die mit der Größe der Flügelsehne vergleichbar ist. Basierend auf diesem Effekt kann sogar eine ganze Klasse von niedrig fliegenden Fahrzeugen - WIG.

Was ist das Wesen des Phänomens? Dieses Problem kann nur gelöst werden, wenn angenommen wird, dass Luft ein komprimierbares Gas ist.

Wenn der Flügel dann über dem Boden fliegt, bildet sich zwischen zwei festen Oberflächen ein Luftspalt begrenzter Größe. Wenn ein Flügel mit einem kleinen positiven Anstellwinkel fliegt, erfährt der entgegenkommende Luftstrom unter dem Flügel eine allmähliche Kompression von der Vorderkante des Flügels zur Hinterkante (siehe Abb. 8).

Der maximale Kompressionsdruck auf dem Strömungssieb unter dem Flügel hängt nur vom Geschwindigkeitskopf relativ zum fliegenden Flügel ab, und dieser Druck in der komprimierten Schicht kann den Druck des Luftgeschwindigkeitskopfs nicht überschreiten:

Po = Vo ^ 2 * Q / 2 ,

wo ist der P-Geschwindigkeitsluftdruck bei der Flügelgeschwindigkeit V, V ist die Flügelfluggeschwindigkeit, Q ist die Luftdichte.

In Kenntnis des maximalen Druckanstiegs unter dem Flügel berechnen wir die geometrischen Parameter im Spalt des "Luftkissens".

Bei einer Geschwindigkeit von 40 m / s (144 km / h) beträgt der Geschwindigkeitskopf Po = 1 kPa oder 1% von 1 atm. (100 kPa).
Das heißt, bei einer Geschwindigkeit von 40 m / s wird der maximale Druck unter dem Flügel durch Kompression um 1% in Höhe X des Abstands von der Vorderkante des Flügels nach hinten erreicht. Auf dem Auge ist eine solche Vorspannung fast nicht nachweisbar, und die Schicht unter dem Flügel erscheint optisch flach (siehe Abb. 8.a).

Der Anstellwinkel beträgt A = (Po / Ratm) * X / V Bogenmaß (bei kleinen Winkeln sinA = A),
Dabei ist B die Flügelsehne, X der Luftspalt zum Boden unter dem Flügel in Höhe der Hinterkante des Flügels, R der Luftgeschwindigkeitskopf bei der Flügelgeschwindigkeit V und Ratm der atmosphärische Druck (auf Meereshöhe Ratm = 100 kPa).

Es stellt sich heraus, dass der maximale effektive Anstellwinkel zum Erzielen eines Bildschirmeffekts von der Höhe des Flügels über der Oberfläche, der strukturellen Breite des Flügels und der gegebenen Fluggeschwindigkeit abhängt und der Anstellwinkel nur eine Ableitung dieser Werte ist.

Schlussfolgerung: Es ist möglich, die Flügelbreite nahezu unendlich zu vergrößern, den Anstellwinkel auf nahezu Null zu reduzieren und so den minimalen Widerstand von Cx mit der praktisch induktiven Komponente des Widerstands zu erreichen.

Der „Bildschirmeffekt“ bei niedrigen Fluggeschwindigkeiten bietet eine sehr hohe Flügelqualität, da er bei extrem kleinen Anstellwinkeln auf einem fast flachen und sehr dünnen Flügel den maximalen spezifischen Auftrieb am Flügel erzeugt, der dem Druckkopf Ro entspricht. Die Qualität des Flügels bei niedrigen Machzahlen während des Fluges auf dem Bildschirm kann K = 25-30 erreichen.
Der Beitrag der Verdünnung über der oberen konvexen Oberfläche des Flügels während eines solchen Fluges auf einem "Schirm" mit einem flachen Flügel ist im Vergleich zum Druck unter dem Flügel ziemlich gering.

Mit zunehmender Fluggeschwindigkeit nimmt der Geschwindigkeitskopf quadratisch zu, und um den maximalen Bildschirmeffekt zu erzielen, muss der Anstellwinkel proportional zur Zunahme des Geschwindigkeitskopfes Po angehoben werden.

Das heißt, das Erhöhen der Geschwindigkeit V0, um Po zu erhöhen, führt zu einer quadratischen Erhöhung der Geschwindigkeit der Erhöhung des Anstellwinkels, was wiederum die Qualität des Flügels stark verringert. Und ab einer bestimmten Geschwindigkeit V-max wird die Stärke des Bildschirmeffekts mit einem großen Anstellwinkel mit der Auftriebskraft eines herkömmlichen Verkehrsflugzeugs im Landemodus mit erweiterter Flügelmechanisierung verglichen.

Für jeden Flügel mit Sehne B ist es zur Erhöhung der Flughöhe X erforderlich, den Anstellwinkel anzuheben. Danach steigt die WIG auf eine neue Höhe X2 an, wobei das Gleichgewicht des Kompressionsgrades des Strahls aufgrund des neuen Anstellwinkels in einer neuen Höhe wieder hergestellt wird. Gleichzeitig beginnt der Flug des Ekranoplan mit zunehmender Höhe, den Flugwiderstand linear zu erhöhen, und die entsprechende erforderliche Schubkraft nimmt auch zu, ohne die Fluggeschwindigkeit zu ändern. Das heißt, die Treibstoffeffizienz des Fluges eines Ekranoplan kann sich ab einer Höhenzunahme von nur wenigen Metern dramatisch ändern. Beispielsweise beträgt die maximale Flugreichweite des Oriole ekranolet in einer Höhe von 0,8 m 1150 km und in einer Höhe von 0,3 m bei gleicher Last bereits 1480 km.



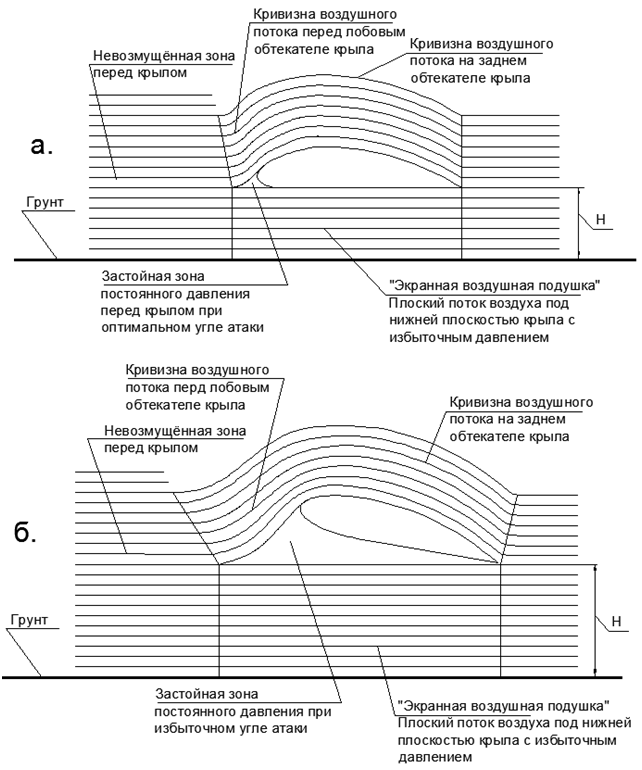Abb. 8. Luftstromkonfiguration für den „Bildschirmeffekt“: a.) Optimaler Anstellwinkel ohne stagnierende Zone unter dem Flügel, b.) Übermäßiger Anstellwinkel, der eine große Blase aus stehender Luft mit hohem Druck zwischen dem Flügel und der Druckluftschicht des „Siebluftkissens“ bildet.

Schlussfolgerung: Ein zusätzliches Aufreißen des Anstellwinkels des Flügels ohne Erhöhung der Fluggeschwindigkeit auf dem Bildschirm führt nicht zu einer Erhöhung des Auftriebs, sondern nur zu einer Erhöhung des Flugwiderstands Cx (siehe Abb. 8.b).

Unter Berücksichtigung des Winkels der Flügelsehne des Verkehrsflugzeugs im Landemodus von etwa 15 Grad können wir das Ausmaß der Kompression des Strahls unter dem Flügel auf den Druck Po und die entsprechende Geschwindigkeit V0 unter Berücksichtigung des Wertes der Sehne B gleich der Höhe des Flügels X abschätzen

15 Grad entsprechen sin15 = 0,262

Bei einem Anstellwinkel von 15 Grad sollte eine Druckhöhe Po = 0,26 atm = 26 kPa vorhanden sein. Diese Drücke werden jedoch bei sehr hohen Geschwindigkeiten (740 km / h) realisiert und überschreiten die für den Flug erforderlichen berechneten Flächenlasten bei weitem. Das heißt, ein derart großer Anstellwinkel zur Landung, um einen Bildschirmeffekt über der Landebahn zu erzeugen, ist bei Landegeschwindigkeiten von 250 bis 300 km / h zu groß.

Die Qualität des Flügels bei einem Anstellwinkel von 15 Grad sinkt auf einen Gesamtwert von K = 3,7.
Die Landegeschwindigkeit des Verkehrsflugzeugs beträgt nur etwa 250 km / h (70 m / s), während die Druckhöhe Po = 3 kPa oder nur 3% von Ratm beträgt, während die normale Tragflächenlast im Flug 5 kPa (500 kg / m.kv = 5% von) beträgt Ratm). Das heißt, bei der Landung beginnt der Pilot den Bildschirmeffekt des Verkehrsflugzeugs in einer Höhe spürbar zu spüren, die der Breite des Flügels B entspricht, vergleichbar mit der Höhe der Fahrwerke. Durch Ausrichten des Flugzeugs und Verringern des Anstellwinkels bei einer Geschwindigkeit von 250 km / h kann das Flugzeug das „Siebluftkissen“ durchdringen, da seine Tragfähigkeit geringer ist als der für den Flug erforderliche Druck unter dem Flügel.
Aufgrund des "Screen-Effekts" tritt "Losslessness" in einem Flugzeug im Horizontalflug ohne Freigabe der Flügelmechanisierung bei einem Anstellwinkel von 5% (oder 3 Grad) bei einer Druckhöhe von Po = 5 kPa auf, was Vo = 324 km / h oder 90 m / s entspricht.

Ein Anstellwinkel von 5% (oder 3 Grad) erzeugt die Qualität eines Flügelflügels gleich K = 20.
Ein hoher K = 30 entspricht einem Anstellwinkel von 3% (2 Grad), während der Gegendruck unter dem Flügel nur 3% beträgt * Ratm = 3 kPa (300 kg / m²), was einem Hochgeschwindigkeitskopf bei V = 70 m / s (250 km / s) entspricht h).

Somit liegen kostengünstige Flugmodi im "Ekranoplan" -Modus im Vergleich zum üblichen "Flugzeug" in großer Höhe in der Niedriggeschwindigkeitszone. Wenn die Qualität des Flügelflügels niedriger als K = 20 ist, ist es rentabler, gewöhnliche Höhenflugzeuge für den Transport zu verwenden. Das heißt, die kostengünstigen Einsatzbereiche von WIGs entsprechen Geschwindigkeiten unter 300 km / h.

Perückenmanöver

Eine separate Überlegung betrifft das Manövrieren von WIG im Flug. Da die Auftriebskraft des Flügels auf dem „Bildschirm“ anders geformt ist als beim Höhenflug, kann er nicht einmal „mit dem Flugzeug“ manövrieren.

Das Ekranoplane kann keine Kurven mit einer Rolle auf dem Flügel legen, da es sofort einen Auftriebsverlust auf dem angehobenen Flügel und die Berührung des Wassers mit abgesenktem Flügel erhält. Für den Ekranoplan ist eine Drehung nur mit einem „Pfannkuchen“ möglich, dh ohne Rolle, aber nur durch die Erzeugung von Seitenkräften aus dem vertikalen Schwanz.

Das vertikale Heck der WIG selbst sollte sich ebenfalls vom Flugzeugheck unterscheiden. Das vertikale Heck der WIG sollte aus mindestens zwei Kielen bestehen, die je nach Art des durchgeführten Manövers sowohl synchron als auch zufällig arbeiten können. Das vertikale Gefieder führt in diesem Fall nicht nur eine WIG-Drehung um seine vertikale Achse aus, sondern erzeugt auch eine horizontale Kraft über die Fluggeschwindigkeitsrichtung.
Das horizontale Gefieder am hinteren Kiel steuert den Anstellwinkel.
Der breite und kurze Flügel muss mit entwickelten Unterlegscheiben ausgestattet sein, die verhindern, dass sich die unter dem Flügel komprimierte Strömung zu den Seiten ausbreitet. Zusätzlich dienen diese Skeg-Unterlegscheiben als Landepontons für das Abspritzen.

Außerdem ist ein zusätzliches horizontales Gefieder an den Enden des Hauptflügels erforderlich, um das Umkippmoment durch die Wirkung des vertikalen Gefieders auszugleichen.

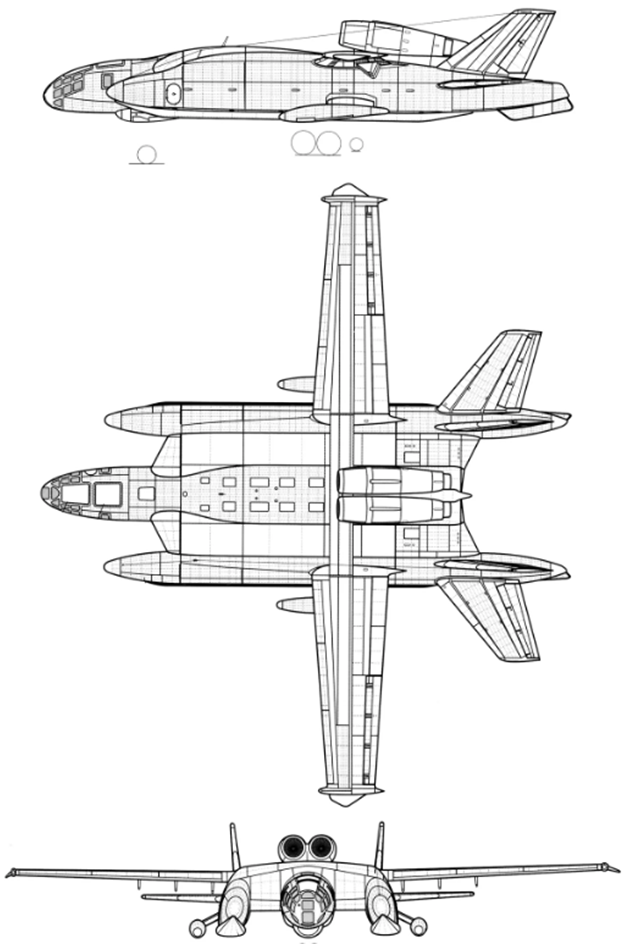
In der Praxis wurde das WIG-VVA-14-Ekranoplane gemäß diesem Schema (siehe Abb. 9) und zahlreichen Versionen vielversprechender Modelle von Ekranoplanes gebaut, bei denen Skeg-End-Unterlegscheiben die Rolle des vorderen vertikalen Tailing spielen (siehe Abb. 10).


a.


b.


c.

Abb. 9 Perücke Bartini VVA-14. A. Zeichnen. b. Modell in 3-D. c. Foto der aktuellen Probe auf dem Wasser.



Abb. 10. Layout verspricht großen Ekranoplan.

Arten von Ekranoplan-Manövern aufgrund des vertikalen Gefieders:

• Zwei Kiele mit identischem Abstand ermöglichen den "Side Shift" -Modus bei gleichzeitiger Drehung in eine Richtung. Gleichzeitig wird das Wingplane ohne Drehung des Rumpfes von einer Spur zur anderen verschoben. In diesem Fall arbeitet das horizontale Gefieder in verschiedene Richtungen und gleicht das Fersenmoment des vertikalen Gefieders aus.
• Wenn die Kiele im gleichen Winkel in verschiedene Richtungen gedreht werden, entsteht ein Drehmoment, das den WIG-Körper um eine vertikale Achse dreht. In diesem Fall funktioniert der horizontale Schwanz nicht, da der Moment vom vertikalen Schwanz nicht auftritt.
• Wenn die Kiele unter verschiedenen vereinbarten Winkeln in verschiedene Richtungen gedreht werden, erfolgt eine Drehung entlang einer Kreisbahn (Zirkulation), wobei der Geschwindigkeitsvektor mit der Richtung der Längsachse des Ekranoplan-Rumpfes zusammenfällt und der Ekranoplan selbst auf einer gegebenen Kreisbahn mit gleichen Winkelgeschwindigkeiten und Rotation des Ekranoplan selbst herumfliegt vertikale Achse.
  
  In diesem Fall arbeitet das horizontale Gefieder in verschiedene Richtungen und gleicht das Fersenmoment des vertikalen Gefieders aus.

Alle diese Modi sind im manuellen Modus praktisch nicht praktikabel, da die geringe Höhe einfach keine Zeit für eine Reaktion im Tempo der menschlichen Wahrnehmung lässt. Um den Ekranoplan zu steuern, benötigen Sie eine Steuerungsautomatisierung, ähnlich der automatischen Stabilisierung von ultra-instabilen Kämpfern der Generation 4-5.

Fazit

Alle obigen Annahmen basieren auf offen veröffentlichten experimentellen Daten (ADT-Druckkurven auf den Flügel und andere Daten).

Im letzten Jahrhundert wurde eine große Menge Geld in die experimentelle Aerodynamik für den Bau von ADT verschiedener Typen und Größen investiert, und eine große Menge an tatsächlichem Material wurde in Experimenten mit Modellen verschiedener Flugzeuge und einzelner Flügelelemente erhalten.

Es ist überraschend, dass sich die Schüler im Unterricht nicht auf die Materialien realer Experimente verlassen, sondern auf zweifelhafte Theorien von vor 100 Jahren. Und das trotz der Tatsache, dass die experimentellen Daten selbst diesen moosigen Theorien eindeutig widersprechen.

Selbst in einem so verallgemeinerten Einführungskurs wie „Einführung in die Aerodynamik“ für FALT FizTech werden qualitative Erklärungsmodelle des Grundkonzepts der „Auftriebskraft des Flügels“ nicht angegeben, sondern durch abstruses wissenschaftliches Jonglieren mit mathematischen Formeln ersetzt (die darüber hinaus keine Berechnung zulassen).

In der Wissenschaft gab es einen Trend zu einer Trennung zwischen theoretischen und praktischen technischen Anwendungen bei der Entwicklung spezifischer Produkte. Die offensichtlichen Widersprüche in den theoretischen Modellen werden nicht beworben, sondern schweigen im Gegenteil in jeder Hinsicht, um die Autorität der moosigen und bereits verstorbenen alten Männer der Akademie der Wissenschaften nicht zu erschüttern und den siegreichen Marsch ihrer aufrichtigen Fehler auf den Seiten recht moderner Lehrbücher und Monographien nicht zu unterbrechen.

PS Nach der Veröffentlichung des ersten Teils dieses Artikels kam eine Diskussion unter dem Artikel, dass ungefähr die gleichen Ideen bereits 2003 von einem Professor in Cambridge geäußert wurden, der dort den Kurs „Aerodynamik“ unterrichtete. In der Nachricht gab es einen Link zu einem Video mit einem Vortrag eines Professors zu diesem Thema sowie einen Link zu einem Artikel, in dem auf der letzten Seite genau die gleiche Methode zur Druckbildung durch einen gebogenen Luftstrom beschrieben wurde, wie ich sie in diesem Artikel beschrieben habe.
Ich war unglaublich erfreut, dass ich jetzt nicht alle Angriffe selbst abwehren muss, aber Sie können sich einfach auf den Cambridge-Professor und seinen Artikel in einer britischen wissenschaftlichen Zeitschrift aus dem Jahr 2003 beziehen.

Hier ist die Nachricht mit den Links:
""
Joehopkins7
24. Februar 2019 um 22:35 Uhr
-1
Als ich verschiedene Videos über Aerodynamik sah, stieß ich auf einen interessanten Vortrag über Aerodynamik von Professor Cambridge.
Bereits 2003 erklärte ein Cambridge-Professor den Studenten der Vorlesung genau die gleichen Gedanken wie der Autor des hier diskutierten Artikels.
Ich habe mich sogar verdächtigt, dass der Autor einfach ein Plagiat ist.
Da er sich in dem Artikel jedoch nicht auf englische Wissenschaftler bezog und diese Videos nicht zu seiner Verteidigung zitierte, können wir an seine ehrliche unabhängige Entdeckung der Entdeckung eines anderen glauben.))

Hier ist ein Link zur Vorlesung
www.youtube.com/attribution_link?a=nfUWqs-6T7M&u=%2Fwatch%3Fv%3DH2RRiF24L4A%26feature%3Dshare&fbclid=IwAR2NOfdqNs0HK9WbCp-OYwy0Y4LYq0q_qqq_q

Es gibt auch einen Link zu einem Artikel, in dem bereits 2003 ein Professor an der Universität von Cambridge in der englischen Fachzeitschrift genau dasselbe schreibt wie der Autor eines Artikels über Habré

www3.eng.cam.ac.uk/outreach/Project-resources/Wind-turbine/howwingswork.pdf
.. "

Die Auftriebskraft des Flügels. Teil 2

Monin Ilya Alekseevich, Ph.D., imoninpgd@gmail.com

Um die Entwicklungsordnung von „Luftfahrt“ als Industriezweig und „Aerodynamik“ als Wissenschaft zu verstehen, muss daran erinnert werden, dass zuerst die ersten von begeisterten Inspirationsingenieuren gebauten Flugzeuge erschienen (siehe Abb. 11) und erst dann Theoretiker auftauchten, die dann schufen Disziplin "Aerodynamik" basierend auf den Ergebnissen der Schaffung von Konstrukteuren.
Auf dem Bild ist das vom Autofahrer Henri Farman entworfene Flugzeug eine Abwandlung des gekauften Kleinflugzeugs von Voisin. Gleichzeitig wurde das erste Flugzeug der Voisin-Brüder erst 1907 produziert. Zum Zeitpunkt des Kaufs von Farman konnten Voisins Flugzeuge nur leicht abprallen und einige zehn Meter fliegen. Nach einer Reihe von Änderungen am ursprünglichen Flugzeug hatte Farman die Möglichkeit, über 1000 m zu fliegen, während er sich noch umdrehte und einen Kreis zur Landung bildete. Farmans Rekordflug fand am 13. Januar 1908 statt. Und bereits 1909 eröffnete die Firma der Brüder Farman eine eigene Produktion von Flugzeugen ihres eigenen Designs und eine Flugschule, um ihnen die Kunst des Fliegens beizubringen (siehe Abbildung 12). Farmans Fluggeschwindigkeit betrug damals etwa 60 km / h, was in einem Rekordflug in einer Entfernung von 180 km gezeigt wurde, der in 3 Flugstunden überwunden wurde.



Abb. 11. Ein Modell von Voisins Flugzeug, das 1907-1908 für einen Rekordflug von Farman umgebaut wurde.




Abb. 12. Das Layout des Flugzeugs "Farman IV-1910". im Museum und ein Foto einer echten Probe am Flughafen.

Es ist klar, dass die ersten frühen Flugzeuge Low-Power, Light und Low-Speed ​​waren.
Diese Parameter entsprechen den ersten konvex-konkaven dünnen Profilen, die der einfachsten gekrümmten Sperrholzplatte ähnlicher sind, und nicht einem komplexen Profil mit einer tiefen theoretischen Fehleinschätzung.
Als Referenz gebe ich ein Beispiel für die Transformation von Flügelprofilen vom frühesten Beginn des 20. Jahrhunderts zur voll entwickelten Luftfahrtindustrie Mitte der 40er Jahre. (siehe Abb. 13)



Abb. 13. Trends im Profil des Flugzeugflügels der ersten Hälfte des 20. Jahrhunderts.

Nach dem ersten leichten Versuchsflugzeug nahm die Größe und Masse der Flugzeuge für den Transport einer immer größer werdenden Nutzlast rapide zu. Dünne Flügel konnten einer solchen Größe und einem solchen Gewicht in keiner Weise standhalten, dass hochfeste Träger im Flügel installiert werden mussten, und der Flügel selbst sollte flach konvex oder sogar doppelt konvex sein, um den Stützbalken hinter dem stromlinienförmigen Flügelsaum zu verbergen.
Bereits in den 20er Jahren nahmen alle Flügelprofile ein völlig modernes Aussehen an.
In den 1940er Jahren hatte sich die Luftfahrtindustrie so stark entwickelt, dass sie begann, eine ganze Armada von Flugzeugen zu produzieren, die ganze Städte in Staub verwandeln konnten. Bei einer derart explosiven Entwicklung der Produktionskapazitäten blieb die theoretische Basis jedoch äußerst schwach.
In den 30er Jahren erlaubte die Intensität der Luftfahrtentwicklung nicht mehr den Bau neuer Flugzeuge auf einer „Ahnung“, sondern erforderte den Bau einer leistungsstarken Versuchsbasis, um Teile von Flugzeugen, Großmodellen und Flugzeugen in riesigen Windkanälen (ADT) vollständig auf den Boden zu blasen.

So wurde 1939 in TsAGI der T-101, der damals größte Windkanal (der zweite der Welt), in Betrieb genommen, der es ermöglichte, das gesamte Flugzeug am Boden mit den damals relevanten Fluggeschwindigkeiten zu untersuchen.
Strömungsgeschwindigkeit 5–52 m / s
Re-Nummer pro 1 m bis 3,6 ∙ 106
Atmosphärischer Gesamtdruck
Kopfdruck bis 1,7 kPa
Umgebungsbremsentemperatur
Anstellwinkelbereich (α) ± 20 °
Schlupfwinkelbereich (β) ± 180 °
Abmessungen des Arbeitsteils:
Düsenabschnitt (Ellipse) 24x14 m
Länge
des Arbeitsteils 24 m Größe der Prüflinge:
Spannweite: bis zu 18 m
Rumpflänge: bis zu 30 m
Tragflächenfläche: bis zu 35 m2

Seitdem sind Flugzeuge viel größer und Fluggeschwindigkeiten viel schneller geworden, so dass kein modernes Flugzeug in die gesamte T-101 ADT passen kann, aber moderner und schneller ADT blasen nur in großem Maßstab Nye Layouts oder einzeln Konstruktionselemente.
Zwar hat sich in der Theorie seit Beginn des letzten Jahrhunderts wenig geändert, so dass die Flugzeugkonstrukteure bereits Ende des 20. Jahrhunderts neu zu erfinden begannen, was die Konstrukteure des frühen bis mittleren 20. Jahrhunderts bereits durchgemacht hatten, aber die Theoretiker hatten es nicht erklärt. Ich werde zum Beispiel eine Profilansicht des Flügels eines Kunstflugflugzeugs geben, der in den 1980er Jahren als der beste angesehen wurde (siehe Abbildung 14).


Abb. 14. Eines der Flügelprofile aus dem Aviation Profiles-Katalog.

Der gleiche wiederkehrende Gedankengang wird auch bei großen Flugausrüstungsmodellen beobachtet, was sich in der Entstehung von Ekranoplanes-Monstern in den 1960er und 80er Jahren äußerte (Abb. 15), die sich nicht von Riesenflugzeugen der späten 1930er Jahre unterscheiden (Abb. 16).
Gleichzeitig wurde der Bildschirmeffekt in den frühen 30er Jahren zum Zeitpunkt der Landung großer mehrmotoriger Flugzeuge mit einem großen Flügelakkord entdeckt.
Der Bildschirmeffekt zeigte sich auch deutlich bei der Landung des Rekord-Langstreckenflugzeugs ANT-25, als das Flugzeug während eines Testfluges im Jahr 1933 einfach nicht landen konnte und wenn die Räder die Räder leicht berührten, prallte das Flugzeug ab und startete erneut. Um diesen Effekt zu beseitigen und eine ruhige Landung zu gewährleisten, mussten sogar spezielle einziehbare Bremsklappen eingebaut werden, die die Flugeigenschaften des Flügels während der Landung stark verschlechtern.
Die Flügelsehne im breitesten Wurzelteil des ANT-25 überschritt die Höhe des Fahrwerks und schuf so ideale Bedingungen für die Bildung eines Bildschirmeffekts unter einem breiten, tief fliegenden Flügel. Gleichzeitig wurde bei der Landung mit leeren Tanks mit einem Flugzeuggewicht von 4000 kg und einer Flügelfläche von 88 m² eine durchschnittliche Flügellast im Flug von weniger als 50 kg / m² erzeugt, was einem Geschwindigkeitsdruck von 500 Pa bei einer Geschwindigkeit von 104 km / h (29 m / s) entspricht. zum Fliegen auf dem Bildschirm. Es ist erwähnenswert, dass das damalige Flugzeug (nach modernen Maßstäben) extrem langsam flog, so dass der Rekord ANT-25 eine Reisegeschwindigkeit von etwa 165 km / h (max. 246 km / h in der Höhe) mit einer Flugreichweite von 10-12.000 km und einer Dauer von 75 km / h hatte. 80 Stunden hintereinander.

A. A.
B. B.
B. B.

Abb. 15. Perücke "Kaspisches Monster": a.) Im Flug. B.) Immer noch auf dem Wasser, volles Gesicht. c.) Stationär in Frontalprojektion.

A. A.
B.


Abb. 16. Riesenflugzeug ANT-20 "Maxim Gorki", 1939 a) Schematischer Abschnitt. B) Fotos am Flughafen und während der Landung.

Stehende Zonen während des Luftstroms um Körper komplexer Form als Werkzeug zur Bildung eines virtuellen Flügelprofils.

Oft gibt es Fälle. Wenn es notwendig ist, Luftströmungslinien um Körper herum zu bauen, deren Form kaum als stromlinienförmig bezeichnet werden kann.
Es ist klar, dass die Luft nicht gehorsam um alle Ecken und Rillen des Körpers strömt, sondern mit sanften Drehungen über die Gruben streift und sie mit Wirbeln zerrissener Ströme stagnierender Zonen füllt.
Wenn wir das Vorhandensein von stehenden Zonen als zusätzliche feste Volumina des Profils selbst berücksichtigen, nimmt die Geometrie der Strömung um die uns bekannten aerodynamischen Elemente eine völlig andere Form an.
Es ist interessant, dass eine solche Methode zum Auffinden eines äquivalenten bedingten Flügelprototyps auch in der vorhandenen angewandten Aerodynamik verwendet wird. In jedem Fall wird die Methode zur Konstruktion eines „fiktiven semi-infiniten Körpers“ um einen festen Flügel im Lehrbuch [3] auf drei Seiten (S. 435-437) beschrieben, während der Rand einer dicken gesperrten Grenzschicht als Grenzen des fiktiven Flügels gewählt wird, dh zum Flügel hinzugefügt wird unsere sehr stagnierenden Zonen in „Trennblasen“ oder turbulenten Zonen mit einer vollständigen Unterbrechung der Strömung über dem Flügel. In diesem Fall wird der Druck auf den festen Flügel aus dem Hochgeschwindigkeitsluftstrom als gleich dem Druck dieses Stroms auf den "fiktiven Körper" angesehen. Es stellt sich heraus, dass der Druck vom Hochgeschwindigkeitsstrahl durch eine ausreichend dicke Schicht inaktiver Luft der grenzhemmenden Schicht (stagnierende Zone) ohne Verzerrung auf den festen Flügel übertragen wird.
Betrachten wir im Detail den Prozess des weichen Flusses um Hochgeschwindigkeitsstrahlen mit unterschiedlichen Profilen von Flügelprofilen und unterscheiden verschiedene „stagnierende Zonen“.
Der Fall der vollständigen Anhaftung des Flusses am Flügel bei kleinen Anstellwinkeln bringt nicht viel Neues mit sich (siehe Abb. 17), aber auf der Frontverkleidung erscheint eine kleine stagnierende Zone, die einem kleinen scharfen Schnabel am runden Kopf des Vogels ähnelt.
Das Element scheint klein zu sein, aber es ist äußerst wichtig, um das Phänomen des "Flusses" im Allgemeinen zu verstehen.
Betrachten Sie das übliche Flügelprofil im Horizontalflug mit deutlich abgetrennten Düsen, zuerst mit einem Anstellwinkel von Null (siehe Abb. 18) und dann denselben Flügel mit einem großen Anstellwinkel (siehe Abb. 20).



Abb. 17. Ein Flügelprofil mit einer Strömung ohne Unterbrechungen in den Flügelebenen, aber mit einer kleinen Zone der vollständigen Verzögerung der Strömung auf der Flügelnase.




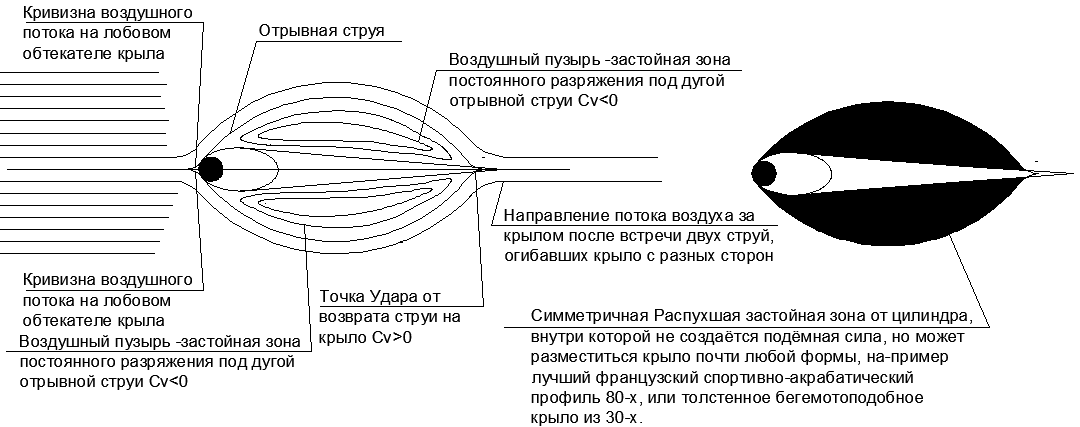Abb. 18. Das Flügelprofil mit Strömung bricht in den Flügelebenen bei einem Anstellwinkel von Null und seinem „fiktiven Körper“.

Betrachtet man den starken Anstieg des „Dummy-Körpers“ im Vergleich zur anfänglichen Druckfrontverkleidung, wird deutlich, wie überraschend wenig Frontwiderstand für lange spindelförmige Körper, beispielsweise für Flugzeugrümpfe, erzielt wird.
Die Straffung solcher Formen erreicht Cx = 0,06, während für eine Kugel mit dem gleichen Querschnitt Cx = 0,4..0,5 und für eine flache Platte Cx = 1 ist.
Es stellt sich heraus, dass die Entladung unter den abgetrennten Düsen in der Frontalprojektion überhaupt nicht erzeugt wird. Alles, was bleibt, ist, den Trennstrahl auf einer geraden Oberfläche parallel zum Geschwindigkeitsvektor zu landen, damit beim Aufprall keine Komponente in Längsrichtung zur Geschwindigkeit erscheint. Ein langer zylindrischer Rumpf mit einer länglichen ovalen Frontverkleidung kommt dieser Aufgabe perfekt nach. Es stellt sich heraus, dass der Luftwiderstand des riesigen Rumpfes dem Widerstand der Kugel an der Spitze der sich verjüngenden Nase entspricht (siehe Abbildung 19.)
Das Verhältnis des Durchmessers der Kugel in der Nasenverkleidung zum Durchmesser des Rumpfes hängt von der Fluggeschwindigkeit ab. Je höher die Fluggeschwindigkeit, desto enger wird die Nasenrundung und drückt den Luftstrom. Die zunehmende Energie der entgegenkommenden Strömung mit einem konstanten Wert des Frontalabschnitts erfordert die Streuung einer immer geringeren Luftmenge an den Seiten des Rumpfes, während ein konstanter Abschnitt des "fiktiven Körpers" hinter der Verkleidung beibehalten wird. Bei Überschall degeneriert der Krümmungsradius des Nasenkegels zu einem Punkt, aber dies ist eine ganz andere Geschichte.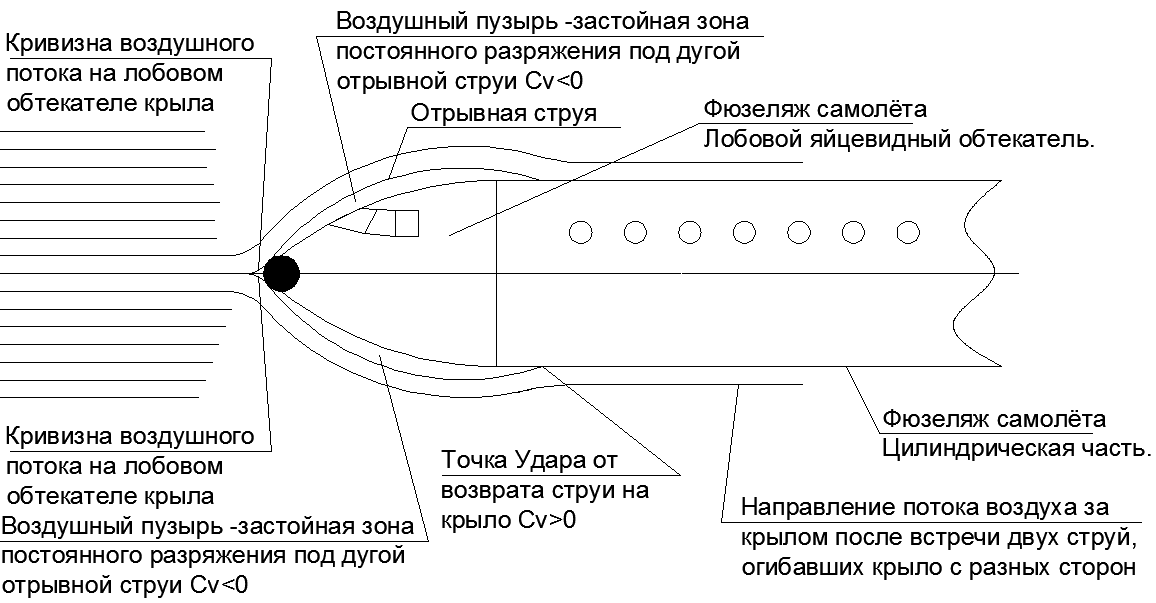



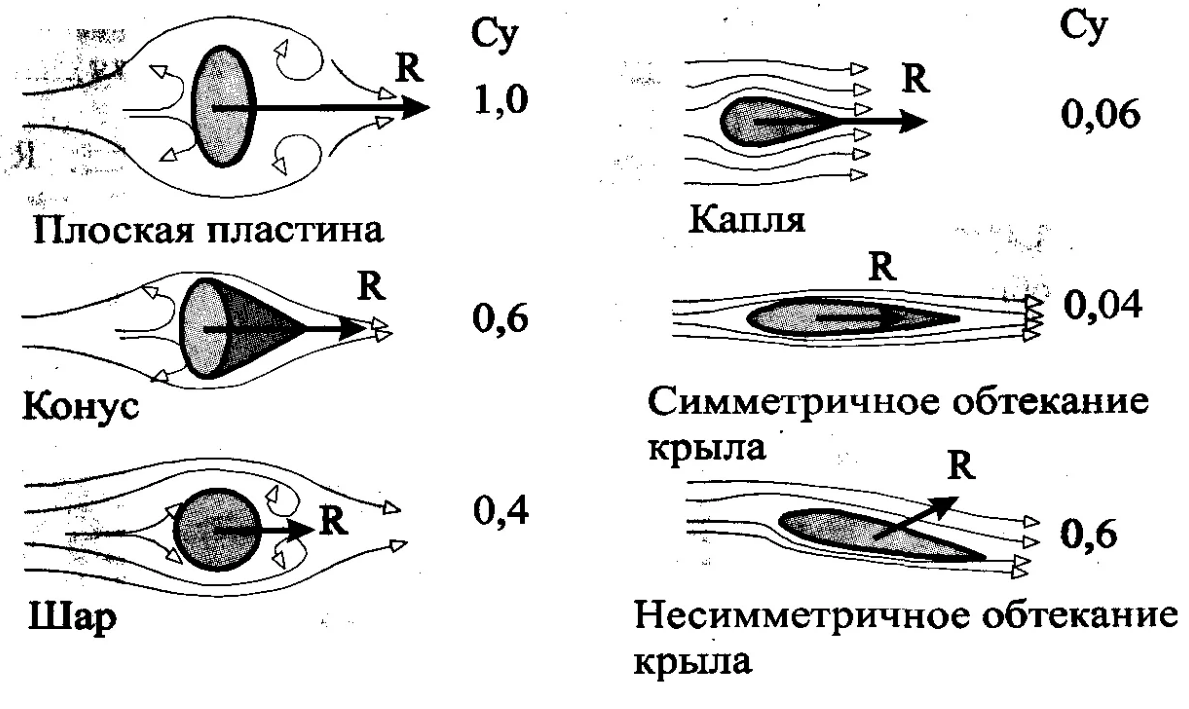
Abb. 19. Die Strömungsart um den Rumpf mit Abreißstrahlen, unter der eine Zone mit einem Flugwiderstand von Null erzeugt wird. Der gesamte Widerstand des Rumpfes entspricht dem aerodynamischen Widerstand des Balls in seiner Nasenverkleidung. Und begleitende Abbildungen aus Lehrbüchern zum Vergleich des Widerstands, wenn Luft um verschiedene Körper strömt.

Wir betrachten nun das Verhalten getrennter turbulenter Zonen mit einem Flügel mit großem Anstellwinkel (siehe Abb. 20).
Zunächst ist es notwendig, die Flugbahn des Trennstroms über der stehenden Zone zu verfolgen, bis er unter dem Flügel des Flugzeugs auf den Fluss trifft. Da wir das Profil der Frontalverkleidung des Flügels als symmetrisch zylindrisch betrachten, haben die Abreißstrahlen die gleiche Kraft und Flugbahn, dh sie sind auch symmetrisch.
Für den horizontalen Flügel haben wir bereits eine symmetrische zweiseitig abnehmbare Blase erhalten, bei der die Düsen am Flügel an denselben Stellen geschlossen wurden.
Wenn der Flügel einen großen Anstellwinkel erhält, ändert sich das Muster der Trennstrahlen. Gleichzeitig beginnen sich die Größen der "getrennten Blasen" = "stehenden Zonen" über und unter dem Flügel dramatisch im Volumen zu unterscheiden.
Infolgedessen wird sich ein sehr geschwollener Flügel mit einer signifikanten Abflachung der unteren Ebene im Vergleich zu der riesigen Kuppel der Trennblase auf der oberen Ebene des Flügels als „fiktiver Körper“ herausstellen. Interessanterweise ähnelt das äquivalente virtuelle Profil eines „fiktiven Körpers“ in einem großen Anstellwinkel des Flügels mit aufgeblasenen, getrennten Blasen auf der oberen Ebene des Flügels überraschenderweise dem bekannten ECIP-Flugzeug. (siehe Abb. 21 )



Abb. 20. Das Flügelprofil mit Strömung bricht auf den Flügelebenen mit einem großen Anstellwinkel und seinem „fiktiven Körper“.






Abb.21. Perücke EKIP. Ein Modell eines perspektivischen WIG-Modells und des aktuellen kleineren WIG-Modells (das aufgrund des Projektstopps nicht gestartet ist).

Das heißt, in Ekranolet ECIP war es eine gute Idee, die stagnierende Zone im hinteren „Schatten“ -Teil des Rumpfes zu kontrollieren, wodurch sich der Abreißstrahl auf dem Flügel im oberen Teil der Kuppel ablagern konnte, was einen größeren Auftrieb bietet und den aerodynamischen Flugwiderstand verringert.
Es stellt sich heraus, dass der Autor des EKIP nicht so erfinderisch war und ein so hippoähnliches Design wie ein Flugzeug anbot.
Das ECIP sollte zwar nicht sehr schnell und in großen Anstellwinkeln des anfänglichen dünnen Profils (ca. 15 Grad) mit einem entsprechend hohen Luftwiderstand fliegen.
Der enorme Laderaum in einem solchen fliegenden Flügel wird für eine gewisse Verschlechterung der Aerodynamik mehr als ausgeglichen. Gleichzeitig sieht der strukturell unschmelzbare Flugzeugflügel viel attraktiver aus als ein herkömmliches Flugzeug, da die Funktionen eines dünnen „Stützflügels“ und eines „Fracht-Passagier-Rumpfes“ voneinander getrennt sind. Aber nur für einen stabilen Flug müssen Sie noch einen langen Strahl hinzufügen, um das Heck aufzunehmen, wie beim riesigen fliegenden Flügel des ANT-20 "Maxim Gorki".
Eine signifikante Ausdehnung des Flügels (eine Erhöhung der Sehne) macht das EKIP-Flugzeug auch in Bezug auf seine aerodynamischen Eigenschaften beim Fliegen in Bodennähe zu einer ausgeprägten WIG. Wenn Sie also auf dem Bildschirm fliegen, verwandelt sich der „fiktive Körper“ des Flügels mit einem großen Anstellwinkel in ein seltsames Eisen, in dem sich der kleine Nasenschnabel der Bremszone des Flügels auf die Größe eines riesigen stehenden Keils unter dem Flügel aufbläst (siehe Abbildung 22).
Die Bildung einer so starken stehenden Zone unter dem Flügel mit einem großen Anstellwinkel ist im Standbild deutlich sichtbar (siehe Abb. 22-2). Link zum gesamten Video www.youtube.com/watch?v=Sd4ycAtYcJA . Es ist deutlich in drei Winkeln zu sehen, während die Rauchfäden vom Motor die Frontverkleidung von unten nach oben und in gleichem Abstand von der Flügelhülle die gesamte Ebene des Flügels von oben einhüllen.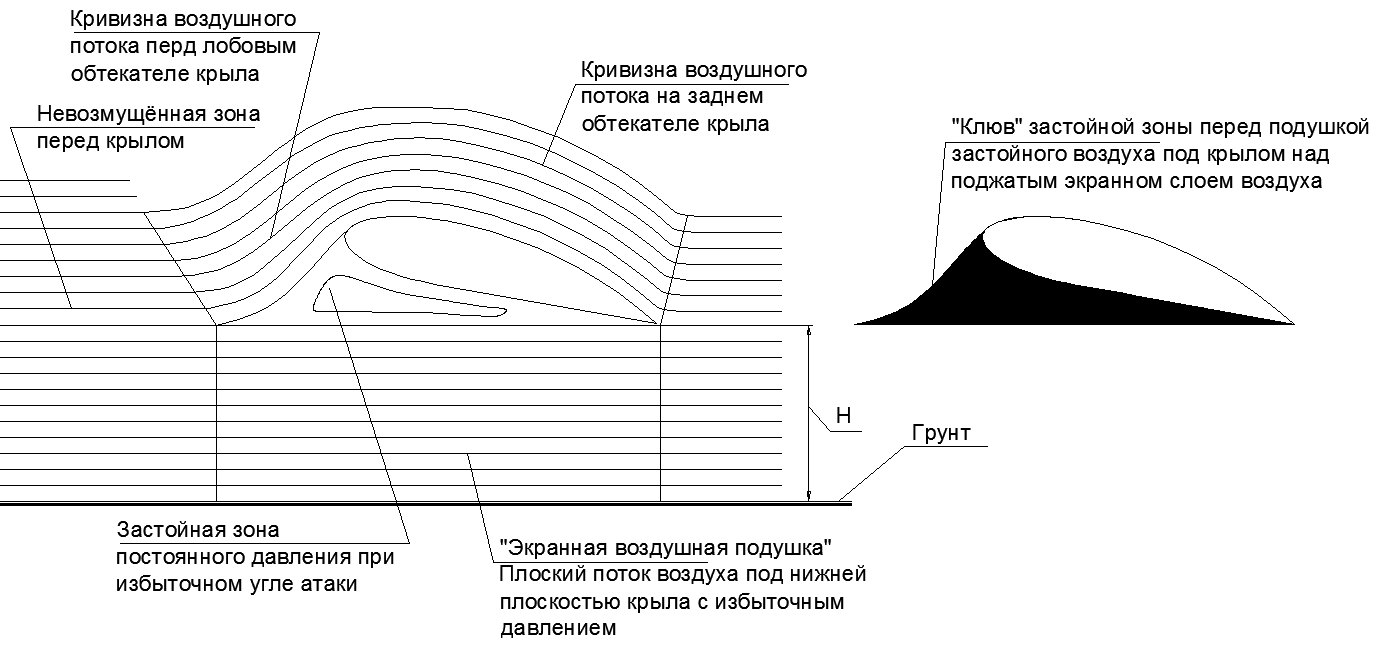


Abb. 22. Das Flügelprofil beim Überfliegen des Bildschirms mit großem Anstellwinkel und dessen "Fiktiver Körper".


Abbildung 22-2. Rauchkabel von Motoren, die zum Zeitpunkt des Starts von der Landebahn beim Start unter dem Flügel einer Boeing 747 hervorkommen.

In diesem spitzen Eisen kann es als Profil von EKIP und VVA-14 Ekranoletos (Bartini) oder als ultradicker Flügel wie der ANT-20 „Maxim Gorki“ platziert werden.
Flugzeuge mit einem sehr dicken Flügel waren in den 1930er Jahren in der UdSSR beliebt, als das größte Vorkriegsflugzeug ANT-20 "Maxim Gorki" geschaffen wurde. Der Flügel dieses Flugzeugs war so dick und breit, dass mehrere Kabinen in den Wurzelabteilen des Flügels platziert wurden, in denen eine Person ihre volle Höhe erreichte (siehe Abb. 16).
Dieses Monster flog zwar mit einer Reisegeschwindigkeit von nur 198 km / h (maximal 220 km / h).
Wenn die ANT-20 die Endabschnitte des Flügels leicht verkürzt und nur den mittig dicksten Teil übrig lässt, sieht das Flugzeug aus wie das spätere Flügel "Kaspisches Monster" Rostislav Alekseev.
Es ist interessant, den eng bemessenen „Maxim Gorki“ aus den 1930er Jahren mit dem „Kaspischen Monster“ aus den 60er Jahren zu vergleichen (siehe Tabelle 5).

Tab. 5. Vergleichende Eigenschaften des Flugzeugs ANT-20 "Maxim Gorky" 1934 und Perücke KM "Caspian Monster" 1966.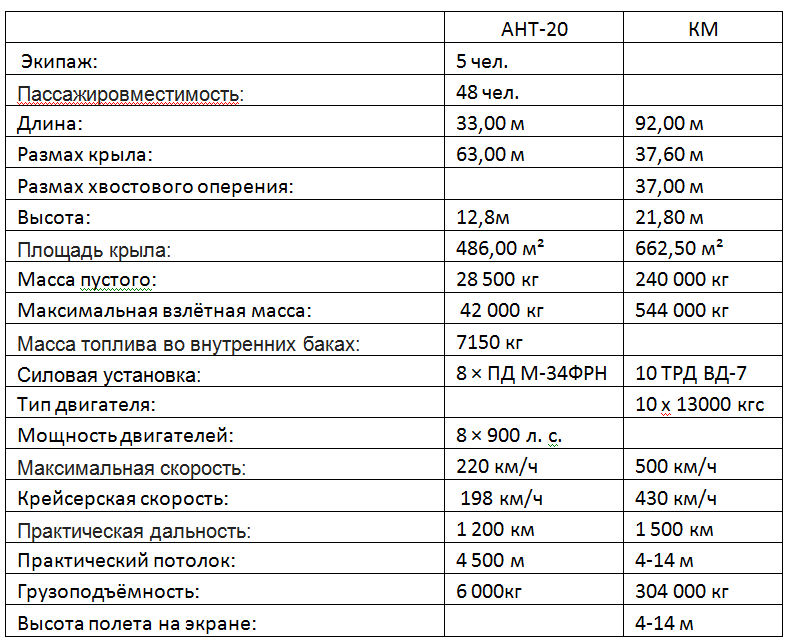


Die Tabelle enthält Referenzdaten, die irgendwie interpretiert werden müssen.
Lassen Sie uns zunächst auf einfache Weise homogene Zahlen direkt durch Teilen vergleichen.
Maximale Masse: 544/42 = 13-fache
Flügelfläche: 662/486 = 1,36-fache
spezifische Flächenbelastung : 13 / 1,36 = 9,5-fache
Reisegeschwindigkeit:
430/198 = 2,17-fache Geschwindigkeitsdifferenz frontal Reisegeschwindigkeit: 2,17 ^ 2 = 4,71-fache
Leistung von Kraftwerken: (10 * 1300 * 9,81 * 430 / 3,6) / (8 * 900 000 * 0,735) = 28,8-fache
Nutzlast unter Berücksichtigung des Kraftstoffs: 304 / (42-28,5) = 22,51.
Praktischer Bereich: 1500/1200 = 1,25
Nach dem Verhältnis des Kraftstoffverbrauchs ist ANT-20 = 7150 / (1200 * 6) = 0,993 l / (t * km)
Völlerei KM nicht bekannt, kann aber durch Leistung und Geschwindigkeit geschätzt werden.
Bei der Berechnung des spezifischen Verbrauchs anhand der Referenzleistung 0,8 kg / (kgf * h) für den Motor VD-7.
Nachbrennerverbrauch beim Beschleunigen aus dem Wasser 10 * 13000 * 0,8 = 104 000 kg / h
Wenn Sie die Dauer eines Reisefluges auf dem Bildschirm berücksichtigen, bei dem nur zwei von zehn laufenden Motoren zum Beschleunigen und Verlassen des Bildschirms zur Verfügung stehen, steigt die Wirtschaftlichkeit.
Für einen Kreuzfahrtflug mit zwei Triebwerken 2 * 13 000 * 0,8 = 20 800 kg / h
Flugzeit 1500/430 = 3,5 Stunden
Während eines Fluges mit einer maximalen Reichweite von 1500 km verschlingt der KM mindestens 104 * 0,5 + 3,5 * 20,8 = 100 Tonnen Treibstoff.
Und die Nutzlast wird etwa 200 Tonnen betragen.
Der Kraftstoffverbrauch von KM beträgt 100 000 / (1500 * 200) = 0,333 l / (t.km).

Schlussfolgerungen aus den erhaltenen Beziehungen:
1. In Bezug auf den Kraftstoffverbrauch kann der KM optimistisch dreimal wirtschaftlicher sein als der ANT-20.
Jetzt verfügt das moderne Verkehrsflugzeug Airbus A380 über eine Frachtmodifikation A380F mit der Fähigkeit, Fracht bis zu 150 Tonnen in einer Entfernung von 10.370 km zu befördern. Die maximale Startmasse beträgt 560 Tonnen (die Masse des Flugzeugs selbst beträgt 280 Tonnen). Aus diesen Indikatoren berechnen wir die Wirtschaftlichkeit für die Frachtversion und geben 130 Tonnen Kraftstoff 150 Tonnen Fracht in einer Entfernung von 10370 km an: 130.000 / (150 * 10370) = 0,0835 l / (t * km).
In Bezug auf die Passagiere unterscheidet sich der Indikator: „Unter den großen Linienschiffen sind drei Liter Kraftstoff pro Passagier und hundert Kilometer (54 Seemeilen) der Strecke am wirtschaftlichsten. Laut Airbus [5] verbraucht der A380 pro Passagier 17% weniger Treibstoff als das „größte moderne Flugzeug“ (anscheinend ist die Boeing 747 gemeint). „„

Das heißt, bei einer Testanzahl von 850 Passagieren mit Gepäck und Sitzen erhalten wir einen Indikator nahe der Berechnung für die Frachtversion.
Es stellt sich heraus, dass wir in den letzten 80 Jahren nicht nur 4-5-mal schneller geflogen sind, sondern auch die Kraftstoffeffizienz mehr als 10-mal von der ANT-20 und 4-mal von Ekranoplan KM verbessert haben. Obwohl vor nur 20 Jahren, flog unser Airbus fünfmal schneller als der ANT-25. Die jüngste Verlangsamung von Passagierflugzeugen ist auf den Kampf um kraftstoffsparende Flüge zurückzuführen.
2. Die Reisegeschwindigkeit des KM wird gewaltsam so hoch eingestellt, dass es bei einer niedrigeren Geschwindigkeit einfach nicht auf dem Bildschirm fliegen kann. Die Flugbedingung auf dem Bildschirm ist die Erfüllung der Ungleichung „Geschwindigkeitskopf“> „Durchschnittliche
Flächenlast “, dh Pv = 8560 Pa bei 430 km / h (120 m / s)> 544000 * 9,81 / 662,5 = 8055 Pa.
3. Die Flugsicherheit eines langsamen Riesenflugzeugs aus den 30er Jahren ist viel besser als die eines übermäßig schnellen geflügelten Flugzeugs aus den 60er Jahren, das fast unkontrolliert zwischen langsam fahrenden Schiffen und den allgegenwärtigen Wasservögeln hin und her rast.
4. Die Kosten für den Betrieb von Ekranoplanen auf See sind viel höher als für Landflugzeuge in großer Höhe. Dies ist auf die übermäßige Anzahl von Triebwerken zurückzuführen, die nur zum Starten aus dem Wasser und zum Erreichen des Bildschirmfluges benötigt werden, sowie auf die extreme Aggressivität des Meerwassers, wenn es Triebwerken und Ekranoplan-Konstruktionen ausgesetzt ist, wenn es in Wolken aus Spritzern von nahegelegenen Meereswellen fliegt.
5. Für den Ekranoplan KM entspricht die Flügelqualität beim Fliegen mit zwei Triebwerken dem Verhältnis ihres Schubes zum Gewicht des Ekranoplan K = 544 / (13 * 2) = 20,9. Somit liegt der aerodynamische Wirkungsgrad eines großen und schweren Ekranoplan auf dem Wirkungsgradniveau der besten modernen Großflugzeuge mit einer Segelflugzeugqualität in der Größenordnung von K = 18-20.
6. Das Rätsel für mich ist die dreifache wirtschaftliche Lücke des Ekranoplan KM zum Airbus 380F: Warum hat der Airbus bei gleicher Qualität der Flugzeugzelle einen viermal besseren Kraftstoffverbrauch?
Oder ist das ganze Geheimnis in der schrecklichen Völlerei alter sowjetischer Turbostrahltriebwerke im Vergleich zu modernen Turbofan-Triebwerken mit einem hohen Grad an Bypass verborgen?

Die Auftriebskraft des Flügels. Teilenummer 3.

Genau ein Jahr ist nach der ersten Veröffentlichung meines Artikels (02/02/2019) über Habré über die Erklärung der Auftriebskraft des Flügels ohne die Bernoulli-Gleichung vergangen.
Ein Artikel für das Jahr hat mehr als 41.000 Aufrufe erhalten und eine führende Position bei der Yandex-Suche nach der Abfrage „Wing Lift“ eingenommen, die unmittelbar nach der Wikipedia-Definition oben auf der ersten Seite angezeigt wird.
Auch in privaten Nachrichten erhielt ich viele wertvolle Informationen und äußerst wichtige Kritikpunkte.
Ich werde die zuvor geschriebenen Teile nicht bearbeiten, aber ich werde einige fehlerhafte Aussagen analysieren, die ich aus denselben fehlerhaften Aussagen von Lehrbüchern dupliziert habe.

Bemerkung 1.
Die Hauptbeobachtung stellte sich heraus, dass ich Bilder von visuellen Vergleichen der aerodynamischen Schleppbewegungen verschiedener Rotationskörper zum Flug falsch zitiert und falsch interpretiert habe.
Daher betrachtete ich diesen Widerstand als den entsprechenden Widerstand von Cx für polare Flugzeuge, und das Bild aus einem Lehrbuch (Abb. 19 im zweiten Teil) zeigt im Allgemeinen die falsche Bezeichnung Su anstelle von Cx.
Sie erklärten mir, dass für einzelne Rotationskörper tatsächlich der Koeffizient Cd geeignet ist, der den Querschnitt (Mittelschiff) des zu blasenden Objekts mit dem von ihm ausgeübten Geschwindigkeitsdruck verbindet.
Der Wert von Cd in den besten Rennwagen fällt nicht unter 0,27.
Darüber hinaus wird für spindelförmige Körper und ein Flügelprofil ohne Hubkraft der Luftwiderstandsbeiwert auf 0,06 bis 0,04 angegeben, was für den Dx-Index niemals erreichbar ist.
Ein so niedriges Su von 0,06 ... 0,04 ist keine direkte Täuschung, aber aufgrund der Verschleierung der Umstände und der Nuancen der Berechnung irreführend. Der Wert von Cd wird also aus dem Verhältnis zum Querschnitt (Mittelteil) berechnet, und der Wert von Cx wird aus dem Verhältnis zur größten Flügelfläche in vertikaler Projektion berechnet, dh zur größten Flügelfläche in Längsrichtung zur effektiven Widerstandskraft.
In farbenfrohen Bildern, die die Straffung verschiedener Körper im Flug demonstrieren, beginnen sie, das „Lange“ falsch mit dem „Roten“ zu vergleichen, dh die Werte in unvergleichlichen Dimensionen zu vergleichen.
Die tatsächlichen Werte des Luftwiderstands Cd, bezogen auf den Abschnitt „Mittelteil“, siehe in der folgenden Tabelle.

Tab. Die Werte der frontalen aerodynamischen Drags von Cd-Körpern verschiedener Formen.
Der linke Tisch ist der Körper der Revolution. Die rechte Tabelle enthält die Balken eines bestimmten Abschnitts.


Bemerkung 2.
Habr ist eine ausgezeichnete Quelle für die Veröffentlichung wissenschaftlicher und technischer Artikel mit verschiedenen Profilen, aber seine Regeln verleihen „negativen Trollen“ überraschend weitreichende Befugnisse, die mit ihren Abneigungen das Karma des Autors in ein tiefes Minus treiben und ihm die Fähigkeit nehmen, auf kritische Kommentare zu reagieren Machen Sie neue Veröffentlichungen Ihrer Artikel. Es gibt sogar Artikel über Habré zu diesem Merkmal von Karma auf Habré.
Infolge des Rückgangs meines Karmas unter -30 wurde ich vom Recht ausgeschlossen, meine eigenen Artikel zu kommentieren, und mir wurde das Recht zur Veröffentlichung entzogen.
Die Ausnahme ist dieser Artikel über Aerodynamik, in dem ich auf wundersame Weise das Recht zum Bearbeiten gelassen habe.
Ich werde dieses „Loch der Gelegenheit“ nutzen, um einen neuen Teil des Artikels zu veröffentlichen, der das negative Karma umgeht.
Sie können alle Ihre Kommentare und Wünsche in „persönlichen Nachrichten“ auf dem Habré selbst oder an meine E-Mail-Adresse imoninpgd@gmail.com senden, die auch am Anfang jedes meiner Artikel angegeben ist.
Ich freue mich immer, höflich auf private Nachrichten mit konstruktiver Kritik zu antworten.

Die praktische Anwendung von Flügeln mit dünnem gekrümmtem Radius in modernen Designs.

Wie sich herausstellte, werden die im ersten Teil betrachteten dünnen konvexen Flügel mit konkavem Radius jetzt aktiv als Drehblätter in großen Windkanälen verwendet (siehe
Abb. 23, 24). Die Abbildung zeigt deutlich, dass genau solche dünnen Blätter zum Drehen der Strömung verwendet werden, wie in mein Artikel.
Es besteht kein Zweifel, dass die Konstrukteure dieser Rotationsschaufeln sich der mechanischen Beanspruchungen bewusst sind, die diese Schaufeln durch die Strömung auf ihnen erfahren.
Es ist zweifellos auch einfach, den Druck auf die Schaufeln aus einem gekrümmten Luftstrom sowohl auf den konvexen als auch auf den konkaven Teilen dieser Schaufeln zu messen. Darüber hinaus kann die Druckmessung sowohl für einen Strom in der Dicke als auch für eine Schaufel von verschiedenen Seiten durchgeführt werden.
Ich glaube, dass es für Menschen mit Zugang zum TsAGI ADT nicht schwierig sein wird, während eines der aktuellen Experimente den Druck von den Schaufeln des ADT-Führungsgeräts durch Wägezellen zu verringern.



Abb. 23. Das Profil des aerodynamischen Blattes, das in einem modernen Windkanal als Schriftsatz-Richtvorrichtung im Luftkanal des ADT verwendet wird.




Abb. 24: Position der Rotationsklingen im ADT-Trakt in der 3D-Visualisierung.


Das Foto (Abb. 25) zeigt die Profile der Rotorblätter einer Gasturbine aus einem bestimmten Lehrbuch zur "Hydro-Gasdynamik", in dem die Strukturelemente von Energiedampf- und Gasturbinen erörtert werden.
Diese Schaufeln wiederholen fast genau das im theoretischen 1. Teil dieses Artikels beschriebene Profil des dünnen, gekrümmten konvex-konkaven Flügels, ebenso wie die Methoden zur Berechnung der Belastung der Schaufeln aus dem Gasstrom in diesen Lehrbüchern zur Hydro-Gasdynamik mit dem im 1. Teil beschriebenen Verfahren übereinstimmen dieser Artikel.
Ein charakteristisches Merkmal des Betriebs der Turbinenrotorblätter ist, dass, wenn sich das Gas um die Oberfläche der Blätter biegt, das Gas selbst die Dichte und Temperatur nicht ändert, sondern nur die Richtung des Gasströmungsgeschwindigkeitsvektors reibungslos ändert, ohne das Gasgeschwindigkeitsmodul zu ändern, wenn wir den Gasfluss in Koordinaten in Bezug auf betrachten die Turbinenschaufel selbst. Das heißt, die Betriebsbedingungen eines einzelnen Turbinenrotorblatts geben praktisch genau die Betriebsbedingungen eines einzelnen dünnen gekrümmten Flügels im freien Luftraum wieder.

Es ist überraschend, dass das, was ich in dem Artikel angegeben habe, seit langem bekannt ist und in angewandten Berechnungen in der Hydrogasdynamik für die Konstruktion von Gasturbinen sowohl für Energietechnik- als auch für Flugzeugtriebwerke weit verbreitet ist, während Anhänger der Aerodynamik diese theoretischen und theoretischen Modelle von " Hydro-Gasdynamik “, wobei„ Aerodynamik “und„ Hydro-Gasdynamik “als unterschiedliche Wissenschaften mit unterschiedlichen Wechselwirkungsgesetzen für völlig identische feste Flügel mit derselben Umgebung von Gasen und Flüssigkeiten betrachtet werden, die sie umgeben.



Abb. 25. Profile der Arbeitsschaufeln einer Gasturbine und Visualisierung des Gasflusses auf ihnen.

Flattern

Während der rasanten Entwicklung der Luftfahrt in den 1930er Jahren trat bei der Verfolgung hoher Geschwindigkeiten unerwartet ein erstaunliches Phänomen namens Flutter auf, als bei einer bestimmten Geschwindigkeit des Flugzeugs plötzlich wachsende Torsionsbiegeschwingungen der Flügel auftraten, die in wenigen Sekunden zur Zerstörung des Flugzeugs führten.
Wir haben dieses Problem mit konstruktiven Methoden gelöst und die Torsions- und Biegesteifigkeit der Flügelstrukturen erhöht. Die theoretischen Erklärungen blieben jedoch auf der Ebene der „intuitiven empirischen Lösungen“, obwohl Akademiker Keldysh für diese Lösungen den Stalin-Preis erhielt.
In den Aerodynamik-Lehrbüchern (siehe Bibliographie) habe ich keine Kapitel gefunden, die das Flattern erklären.
Daher werde ich Erklärungen für das Flutter-Phänomen geben, die nicht auf einer offiziellen Theorie beruhen, sondern lediglich die Konsequenzen aus den im ersten Teil des Artikels beschriebenen theoretischen Bestimmungen ableiten.
Wie im ersten Teil beschrieben, läuft ein Strom mit einem Krümmungsradius von mindestens
Rp = 2 * Robt auf die Frontverkleidung .
Wobei Robt der Radius der Abrundung des Baldachins der Flügelverkleidung ist.
In diesem Fall beträgt die Dicke der Strömung, die in jede Richtung vom Flügel abgelenkt wird, Hp = Robt.
Aus der geometrischen Konstruktion folgt, dass der Winkel des Geschwindigkeitsvektors der getrennten Strömung beim Berühren ihrer Verkleidung mit der Flugrichtung A = 48 Grad beträgt.
Die vertikale Projektion der Geschwindigkeit der getrennten Strömung ist Vp. vert = Vp * sin A = 0,743 * Vp.
Das heißt, wir haben eine obere Schätzung der Vertikalgeschwindigkeit für die Trennströmung erhalten, da die Kriterien für die Grenzschätzung für den Radius der gekrümmten Strömung R = 2 * mit der Dicke der Strömung, die zu einer Seite der Strömung = abgelenkt wurde, bereits in unserer Wunde erhalten wurden.
Während einer weiteren Bewegung über das gekrümmte Profil des Flügels sollte eine getrennte Strömung mit der Anfangsenergie
Ep.vert. = Vvert. ^ 2 * q *
sie aufgrund der Arbeit des Unterschieds des Umgebungsluftdrucks und des Drucks auf der Flügeloberfläche unter der getrennten Strömung, d. H. Aufgrund der Arbeit, löschen Druck über der Flügelebene ablassen.
Evozd = Notre * Rzoez
Das heißt, die Gleichheit E.vert sollte erfüllt sein = Ezvoz
Vvert.p ^ 2 * q * = Notre * Rzd Die
Höhe der umhüllten Blase, ohne den Fluss aus dem Profil zu blockieren : Notr = Vp
. ^ 2 * q * Robt / Rzd
Substituting Ausdruck für Vp. vert = Vp * sin A erhalten wir:

Notre = (Vp * sin A) ^ 2 * q * Rbt / Rzvd = Vp. ^ 2 * q * sin A ^ 2 * Rbt / Rzvod
Das heißt, bei einer Profilhöhe über diesem Wert fließt der Fluss herum ohne die Bildung einer Abreißblase.
Wenn der Wert des Profilhöckers hinter der Frontverkleidung niedriger als der Notre-Wert ist, fließt die Strömung um das Profil herum, wobei sich eine Luftblase mit Entladung und stehender Luft im Inneren bildet, die durch die Schwingungen der Seide visuell erfasst wird.
Als nächstes stellt sich die Frage nach der Länge der stehenden Blase unter der getrennten Strömung.
Wenn wir annehmen, dass der Luftdruckabfall konstant ist, wird das Bremsen des Luftstroms gleichmäßig beschleunigt und die Kurve der Grenze der Trennblase sieht aus wie eine Parabel mit ihrem Buckel nach oben.
Die Zeit der vollständigen Verzögerung der Strömung vertikal ist T = V vert / A.vert
Wobei A.vert = Rvozd / (Robt * q)
Wir erhalten Tpuz1 = Vvert / A.vert = Vvert * (Robt * q) / Razvo
Die Länge der Abreißblase Lpuz1 zum Gipfel ist
Lpuz1 = Vp * Tpuz1 = Vp * V vert * (Robt * q) / Rvozd = V * (V * sin ) * Robt * q / Rzvoz =>
Lpuz1 = V ^ 2 * q * sin * Robt / Rvozd
Aus der erhaltenen Formel Luz1 für die Länge des aufsteigenden Teils der getrennten Strömung über der abgetrennten Blase (oder dem idealen Profil) können wir schließen, dass für einige Werte der Fluggeschwindigkeit V und der Dicke der Frontverkleidung Robt eine Situation auftreten kann, dass der Wert der abgetrennten Blase L bel 1 + 2 = 2 * Lpuz1 kann die Flügelbreite Vkr überschreiten.
Wenn die Ausdehnung der Abreißblase die Hinterkante des Flügels erreicht und die fallende Strömung des Abreißblatts die Hinterkante des Flügels hinterlässt, tritt Hochdruckluft unter der Abreißblase von der verwickelten Spur ein.
Nach dem Druckausgleich in der Trennblase mit der Atmosphäre wirkt die Druckdifferenz zwischen der Atmosphäre und der Blase über dem Flügel nicht mehr auf den Trennstrom. Danach löst sich der Abreißstrom von der Verkleidung und kann nicht mehr zum Flügel zurückkehren, wodurch ein vollständiger Strömungsabriss entsteht.
Bei einem Hochgeschwindigkeits-Horizontalflug über der berechneten Normalgeschwindigkeit für ein bestimmtes Flugzeug mit einem solchen Strömungsabriss über der oberen Ebene des Flügels entwickeln sich weitere Ereignisse in der folgenden Reihenfolge (siehe
Abb. 26 ): - Separate Strömungen bilden Detonationsblasen unterschiedlicher Größe auf dem Flügel mit einem kleinen Anstellwinkel resultierende Gesamtauftriebskraft des Tragflügels Fk1 = Fk.verh- Fk.niz, und Drehmoment auf die DH bezüglich den berechneten Wert durch den Hebel L1
- Wenn auf Vph Beschleunigung über der oberen Ebene des Flügels otryvnooe über die Hinterkante erreicht hat , und p vnodeystvuyuscha Fk2 größer wird als die geschätzte Fk1. Auch das Flügeldrehmoment aus der Erhöhung des Arms L2 steigt signifikant an, wodurch das Tauchmoment erhöht wird.
- Wenn der Durchfluss zum Stillstand kommt, verschwindet die Auftriebskraft aus dem Vakuum in der oberen Trennblase.
- Bei einem starken Verschwinden des Vakuums über der Oberseite des Flügels erfolgt eine sofortige Entlastung der Flügelstrukturen nur auf einer Seite.
- In der unteren Ebene des Flügels tritt noch kein Strömungsabriss auf, und daher setzt sich eine signifikante aerodynamische Kraft von der entwickelten Trennblase nach unten fort, die um ein Vielfaches größer ist als die normale Auftriebskraft des Flügels.
Somit gibt es eine scharfe Überlastung des Flügels, um sich zur anderen Seite zu biegen, dh nach unten, wobei sich der Flügel zur Kurve dreht.
Infolgedessen fällt das Flugzeug stark nach unten, hebt die Nase und verliert an Geschwindigkeit.
Wenn der Flügel mit der Hinterkante nach unten gedreht wird, nimmt der Anstellwinkel des gesamten Flügels stark zu, wodurch die Bremsung des Luftstroms stark zunimmt, während die Trennblase zusammenbricht und die Auftriebskraft an der Unterseite des Flügels ihr Vorzeichen stark ändert. Biegen Sie den Flügel wieder stark nach oben.
Wenn die normale Auftriebsrichtung wiederhergestellt ist, beginnt sich der Flügel stark nach oben zu biegen, und der Moment der neu erzeugten normalen Auftriebskräfte dreht den Flügel und dreht den Flügel mit dem gesamten Flugzeug aus der Tauchkabine.
Damit schloss sich der Zyklus und ging in die zweite Runde.
Das Flugzeug beschleunigt, der Fluss wird wiederhergestellt, ohne entlang der oberen Ebene des Flügels abzuwürgen, und nachdem eine neue kritische Geschwindigkeit erreicht wurde, tritt erneut ein Abwürgen auf, und das Biegen von Überlastungen des Flügels durch Verdrehen wird wiederholt.
Solch ein schnell fließendes Schütteln mit abwechselnden Biegungen und Verdrehungen der Flügel (mit Lasten, die um ein Vielfaches höher sind als die berechnete statische Aufladung) führt zwangsläufig zur schnellen Zerstörung der Flügel.



.26. :
1) F1 , .
2) F2 . F2 L2 .
3) . - . F3 , .
4) Mit einem starken Anstieg des Anstellwinkels des Flügels löscht der einströmende Luftstrom die Trennblase mit verringertem Druck auf die untere Ebene des Flügels, wodurch die Auftriebskraft die Richtung zur Normalen ändert, d. H. Nach oben, wobei das Drehmoment auf den berechneten Tauchgang wiederhergestellt wird.

Es ist eine solche zyklische, sich schnell wiederholende Torsionsbiegeflügelschwingung bei einer bestimmten kritischen Geschwindigkeit Vf, die sie Flutter nennen.
Eine Zerstörung des Flügels durch Flater kann durch eine scharfe Verstärkung der Flügelstrukturen vermieden werden. Dies ist die Empfehlung auf der „intuitiv empirischen Ebene“, die Keldysh gemacht hat.
Gleichzeitig wird nicht nur die Festigkeit in Bezug auf die Festigkeit der statischen Belastungen des Flügels erhöht, sondern auch die Biege- und Torsionssteifigkeit der Flügel, wodurch die im Flügelschlag angesammelte Energie verringert wird, wodurch die Schwellenenergie der Flügelzerstörung verringert wird.
Um die Torsionssteifigkeit zu erhöhen, verwenden Sie am besten ein Rohr oder einen Kasten mit geschlossenem Regelkreis. Eine stärkere Torsionstorsion der "Box" ist viel schwerer als die "Traversen", die in Niedriggeschwindigkeitsflugzeugen früherer Bauart verwendet werden.
In späteren und fortgeschrittenen Flugzeugkonstruktionen stellt sich heraus, dass die gesamte äußere dicke Blattflügelummantelung eine geschlossene Torsionsbox ist, wobei tragende Träger und Versteifungen vom Typ Fachwerk oder Doppel-T-Stück innerhalb des Flügelvolumens verwendet werden. Die Verwendung einer Blattflügelummantelung als tragendes Kraftelement erhöht die Steifigkeit der Struktur dramatisch und reduziert gleichzeitig das Gewicht des gesamten Flügels.
Übrigens werden im Amateurflugzeugbau mit einer Film- oder Stoffummantelung eines Flügels auch heute noch sehr oft dünnwandige Rohre als tragender Hauptträger eines Flügels verwendet.
Das Vermeiden des Auftretens von Flattern bei der gewünschten Geschwindigkeit kann erreicht werden, indem das Flügelprofil in Richtung der Verringerung des Radius des Frontverkleidungs-Robt geändert wird, was zu einer Erhöhung der Schwellengeschwindigkeit Vf für ein neues Flügelprofil führt.
Nach den durchgeführten Berechnungen ist es nicht möglich, den Flater im Horizontalflug vollständig zu meiden, aber es ist durchaus möglich, seinen Einfluss zu verringern, um die Höchstgeschwindigkeitswerte zu erreichen.
Ein solcher Grenzwert ist die Schallgeschwindigkeit, nach der sich die Strömung um den Flügel dramatisch ändert und das Flattern im Unterschallgeschwindigkeitsbereich bleibt.
Während des Überschallfluges sind beide Flügelebenen informativ getrennt, da niederfrequente Druckwellen (niederfrequente Schallwellen mit einer großen Wellenlänge) von zyklischen Ständen den Überschallflügel nicht überholen und die Gleichmäßigkeit der Luftmassen vor dem fliegenden Flügel stören können.
Selbst wenn die Flügelebenen im alternativen Modus des vollständigen Abwürgens arbeiten, hört das Flugzeug nach dem Übergang der "Schallmauer" auf, stark zu zittern.
Als sich die Piloten auflösen, setzt nach dem Passieren der Schallmauer nach qualvollem Zittern plötzlich Stille ein.
Aufgrund der grundsätzlichen Unvermeidlichkeit des Flatterns wird das Fliegen mit gefährlichen transsonischen Flattergeschwindigkeiten für eine sehr kurze Zeit empfohlen, was durch eine schnelle Beschleunigung auf Überschall bei vollem Schub oder durch eine schnelle Verzögerung von Überschall auf das Niveau der Vorflachergeschwindigkeit erreicht wird.
Solche schnellen Durchgänge des Flatergeschwindigkeitsbereichs stellen die minimale Dauer der Exposition gegenüber Vibrationen durch Flattern an Flugzeugstrukturen bereit.


Mit abnehmendem Radius der Frontverkleidung Robt verschwindet das Flatterphänomen selbst nicht vollständig, sondern verschiebt sich in Richtung höherer Geschwindigkeiten.
In den 1930er Jahren war für die schnellsten Jäger das Flattern bei Geschwindigkeiten von 300 bis 400 km / h relevant, wenn genügend Motorleistung vorhanden war, um kleine Leichtflugzeuge auf kritische Geschwindigkeiten zu verteilen.
Mit einer Verringerung der Größe des RPT auf dem Flügel wurden viel schnellere und höher gelegene Jäger erhalten, wie beispielsweise die MiG-3 des Modells von 1940.
Die Bezahlung für die Geschwindigkeit für neue Hochgeschwindigkeitsflugzeuge war jedoch ein geringerer Auftrieb bei niedrigen Geschwindigkeiten, was höhere Geschwindigkeiten bei der Landung erfordern würde.
Es ist jedoch unmöglich, die Lande- und Startgeschwindigkeit auf unbefestigten Flugplätzen zu erhöhen!
Um dieses Problem zu lösen, mussten Ergänzungen in Form von auslenkbaren Platten - „Klappen“ und „Lamellen“ - speziell für den Start- und Landemodus in die Flügelstruktur neuer Hochgeschwindigkeitsflugzeuge eingeführt werden. Klappen und Lamellen hoben den Flügelhub bei niedrigen Geschwindigkeiten mit großen Anstellwinkeln stark an, verschlechterten jedoch die Qualität des Flügels.
Das Rennen um Geschwindigkeit und der Kampf gegen das Flattern führten zu einem schwereren Flügel, der den Flügel verstärkte und komplizierte, um akzeptable Ein- und Landegeschwindigkeiten zu gewährleisten, was ebenfalls zum Gewicht des Flugzeugs beitrug.
Zum Vergleich können wir den Jäger anhand eines einfachen Designs der I-16-Doflater-Geometrie und der schnelleren und komplexeren MiG-3 (mit Lamellen und Klappen in der Ausrüstung) bewerten. Bei nahezu gleicher Motorleistung hatte der erste eineinhalb Mal weniger Masse und gleichzeitig eine um 75 bis 170 km / h niedrigere Geschwindigkeit (420 km / h am Boden und in einer Höhe von 470 km / h), die stromlinienförmiger und schneller und daher komplexer und komplexer war schwerere MiG-3 (in Bodennähe 495 km / h, in einer Höhe von 640 km / h).
Das Verhältnis der Höchstgeschwindigkeit von MiG-3 und I-16 beträgt 495/420 = 1,18.
Darüber hinaus ist gemäß der erhaltenen Formel die Länge der Abreißblase proportional zum Quadrat der Geschwindigkeit, dh eine Erhöhung der Geschwindigkeit um 20% verlängert die Abreißblase um das 1,44-fache.
Das heißt, für eine solche Geschwindigkeitssteigerung von 20% ohne Abwürgen und Flattern muss man entweder den Flügel 1,5-mal ausdehnen (was in der Regel strukturell unmöglich ist) oder den Rundungsradius der Nasenverkleidung und die Gesamthöhe des Profils um das 1,5-fache verringern.
Auf diese Weise wurde das MiG-3-Beschleunigungsproblem gelöst, indem die Dicke des Flügels im Vergleich zur I-16 verringert wurde, während die Breite des Flügels praktisch nicht verändert wurde.
Eine solche Verringerung der Höhe der tragenden Flügelträger um das Eineinhalbfache und sogar bei einer Erhöhung der Masse des Flugzeugs um das Eineinhalbfache erfordert zwangsläufig eine Vergrößerung des Querschnitts der am stärksten belasteten horizontalen Regale von I-Trägern um etwa das 2,5-3-fache, was zwangsläufig zu einer merklichen Erhöhung des Gewichts der Flügelstruktur führt im Allgemeinen.
Heutzutage fliegen moderne Unterschall-Airbusse mit einer Geschwindigkeit von 800-900 km / h, ohne die für ihr Flügelprofil charakteristische kritische Geschwindigkeit Vph zu erreichen. Ein geringer Widerstand gegen den Luftstrom aus dem dünnen Flügel und das Fehlen von Flattern bei hohen Geschwindigkeiten führen zu einem geringen Auftrieb bei niedrigen Start- und Landegeschwindigkeiten. Dies erfordert auch die Installation einer fortschrittlichen Flügelmechanisierung aus einer Reihe von Klappen und Lamellen, die im Start- und Landemodus vom Flügel heruntergezogen werden.
Ein bemerkenswerter Moment von der Manifestation des Flatterns kann als erhöhte Aufmerksamkeit in der UdSSR für einen wissenschaftlichen und experimentellen Ansatz für das Design in der Luftfahrt angesehen werden.
Die Unfähigkeit, Flatterphänomene auf diesem theoretischen Niveau zu erklären, machte es dringend erforderlich, den Flug neuer Flugzeuge unter sicheren Laborbedingungen zu simulieren. Infolgedessen wurde 1939 der größte Windkanal der Welt (der zweite für heute) T-101 in TsAGI gebaut. Die Ironie ist jedoch, dass der T-101 zum Zeitpunkt der Inbetriebnahme bereits moralisch veraltet ist, da seine Geschwindigkeitsmodi (maximal 52 m / s oder 187 km / h) weit hinter den Höchstgeschwindigkeiten in der Luftfahrt Ende der 1930er Jahre und in ihrer Größe zurückliegen Flugzeuge sind in diesen Jahren bereits der Größe der Versuchszone von ADT entwachsen. Infolgedessen ist es bei diesem größten ADT unter realen Bedingungen möglich, nur kleine Jäger und Sportflugzeuge zu testen, und selbst dann nur bei langsamen Starts und Landungen.
Die Aerodynamik moderner Flugzeuge und das Regime des Luftstroms um sie herum müssen anhand separater Fotos von Flugzeugen mit ausgeprägten Nebelschwaden untersucht werden (siehe Abb. 27).
Es ist fast unmöglich, einen solchen Effekt in ADT in vollem Umfang zu erzielen.
Dieses Phänomen wird als Prandtl-Glauert-Effekt bezeichnet - Kondensation von Luftfeuchtigkeit hinter einem Objekt, das sich mit transsonischen Geschwindigkeiten bewegt. Der Effekt wird am häufigsten in Flugzeugen beobachtet, kann aber auch bei niedrigeren Geschwindigkeiten spürbar sein, selbst in Autos. So kann unter Bedingungen sehr hoher relativer Luftfeuchtigkeit der Effekt bei viel niedrigeren Geschwindigkeiten beobachtet werden, beispielsweise auf die aerodynamischen Elemente von Autos während Formel-1-Rennen bei Regenwetter.
In Überschallflugzeugen wird dieser Effekt ebenfalls beobachtet, zeigt jedoch ein völlig anderes Bild von nebligen Verdünnungszonen, das deutlich durch die Linien der frontalen Stoßwellen auf den Frontflächen und der nachlaufenden Stoßwellen begrenzt ist, wenn sie von der Hinterkante des Flügels absteigen. (siehe Abb. 28) Abb


. 27. Flug eines modernen Jägers mit Mechanisierung bei hohen Anstellwinkeln bei niedriger Geschwindigkeit. Die Verdünnungszonen über dem Flügel werden durch intensiven Niederschlag von Nebel unter dem Flügel der Hochdruckzone ohne Beschlagen ausgedrückt. Die Richtung des Luftstroms unter dem Flügel des Flugzeugs wird durch neblige Schnüre von Raketen, die am Boden des Flügels hängen, gut überwacht.




.28. ( — ). — . - 100%.

Bibliographie:

• « », .., , , 1986.-413.
• «» 1, .., , , 2018,-496.
• «», . .., , ...,2017,-607.