Funktionsweise von PageRank: Implementierung in R über lineare Algebra und die Potenzmethode

Hallo Habrowsk-Bürger!

Ich heiße Alex Diesmal habe ich in ITAR-TASS vom Arbeitsplatz aus gesendet.

In diesem kurzen Text werde ich Ihnen die Methode zur Berechnung des PageRank © (im Folgenden als PR bezeichnet) anhand einfacher, verständlicher Beispiele in der Sprache R vorstellen. Der Algorithmus ist ein geistiges Eigentum von Google, wird jedoch aufgrund seiner Nützlichkeit für Datenanalyseaufgaben viele Aufgaben verwendet Dies kann darauf reduziert werden, nach großen Knoten im Diagramm zu suchen und diese nach Wichtigkeit zu ordnen.

Die Erwähnung eines großen Unternehmens in einem Beitrag ist keine Werbung.

Da ich kein professioneller Mathematiker bin, verwende und empfehle ich diesen Artikel und dieses Tutorial als Leitfaden.

Intuitives Verständnis von PR

Es ist nicht schwer zu verstehen, wie das funktioniert. Es gibt eine Reihe von Elementen, die miteinander verbunden sind. Hier erfahren Sie, wie genau sie miteinander verbunden sind - dies ist eine umfassende Frage: Möglicherweise können durch Links (wie Google), möglicherweise durch Verweise aufeinander (fast dieselben Links) die Wahrscheinlichkeiten von Übergängen zwischen Elementen (Matrix des Markov-Prozesses) a priori angegeben werden, ohne die physikalische Angabe zu machen Bedeutung der Kommunikation. Ich möchte diesen Elementen ein bestimmtes Kriterium von Bedeutung zuweisen, das Informationen über die Wahrscheinlichkeit enthält, dass dieses Element von einem abstrakten Teilchen besucht wird, das sich während des Diffusionsprozesses durch den Graphen bewegt.

Ähm, das klingt nicht sehr klar. Es ist einfacher, sich vorzustellen, wie ein Mann einen Laptop mit einer Mohnblume benutzt , auf den Seiten der Suchergebnisse surft, eine Wasserpfeife raucht, Links von einer Seite zur anderen folgt und immer häufiger auf derselben Seite (oder mehreren Seiten) erscheint.

Dies liegt an der Tatsache, dass einige Seiten, die er besucht, so interessante Informationen in der Originalquelle enthalten, dass andere Seiten gezwungen sind, diese mit einem Hinweis auf den Link erneut zu drucken.

Ein solcher Typ in Google wurde Random Surfer genannt. Er ist ein Teilchen im Diffusionsprozess: eine diskrete Änderung der Position auf dem Graphen im Laufe der Zeit. Und die Wahrscheinlichkeit, mit der er die Seite mit einer Diffusionszeit besucht, die gegen unendlich tendiert, ist PR.

Einfache Implementierung der PR-Berechnung

Lassen Sie uns zustimmen - wir arbeiten mit 10 Elementen in einem so kleinen, gemütlichen kleinen Diagramm.

# clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark) 

Jedes der 10 Elemente (Knoten) enthält 10 bis 14 Verweise auf andere Knoten in zufälliger Reihenfolge, ausgenommen sich selbst. Im Moment entscheiden wir nur, dass die genannten Daten ein Weblink sind.

Es ist klar, dass es vorkommen kann, dass ein Element häufiger erwähnt wird als andere. Überprüfen Sie dies heraus.

Ich empfehle übrigens, das Paket data.table für Experimente zu verwenden. In Verbindung mit den Prinzipien von tidyverse läuft alles effizient und schnell ab.

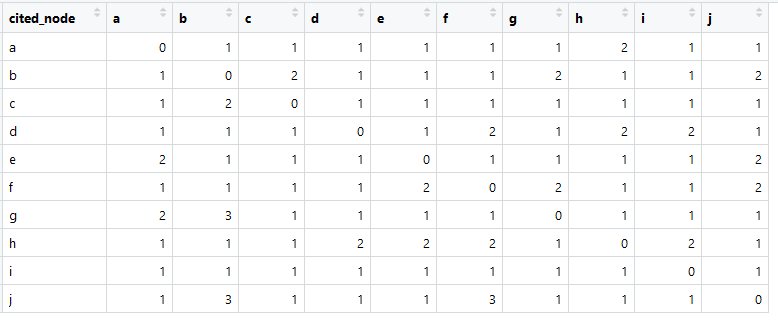
So sieht unsere Linkmatrix aus (im Englischen meistens Adjazenzmatrix genannt).

Die Summe in jeder Spalte ist größer als Null, was bedeutet, dass von jedem Element eine Verbindung mit einem anderen Element besteht (dies ist wichtig für die weitere Analyse).

> anwenden (dt [, - 1, mit = F], 2, Summe)
abcdefghij
11 14 10 10 11 13 11 11 11 12

Basierend auf dieser Tabelle können wir die sogenannte Affinitätsmatrix oder unserer Meinung nach die Proximity-Matrix (und sie wird auch als Übergangsmatrix bezeichnet) erstellen, die Mathematiker die stochastische Matrix (spaltenstochastische Matrix) nennen: Hauptquelle

Weisen Sie es einer Variablen mit dem Namen A zu.



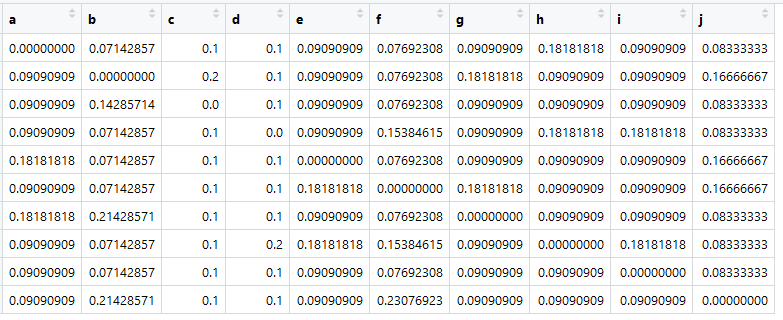
Das Wichtigste ist jetzt, dass die Summe in allen Spalten gleich eins ist.

> Spalten (A)
abcdefghij
1 1 1 1 1 1 1 1 1 1

Hier ist es - eine Matrix von Übergängen, es ist Markov, es sind Ähnlichkeiten. Abbildungen sind die Wahrscheinlichkeiten von Übergängen von einem Element in einer Spalte zu einem Element in einer Zeile.

Dies sind natürlich keine wirklichen "Ähnlichkeiten". Die Gegenwart wäre zum Beispiel, wenn wir den Kosinus des Winkels zwischen der Präsentation von Dokumenten berechnen würden. Es ist jedoch wichtig, dass die Übergangsmatrix auf (Pseudo-) Wahrscheinlichkeiten reduziert wird, damit die Summe über jede Spalte gleich eins ist.

Schauen wir uns das Markov-Übergangsdiagramm (unser A) an:



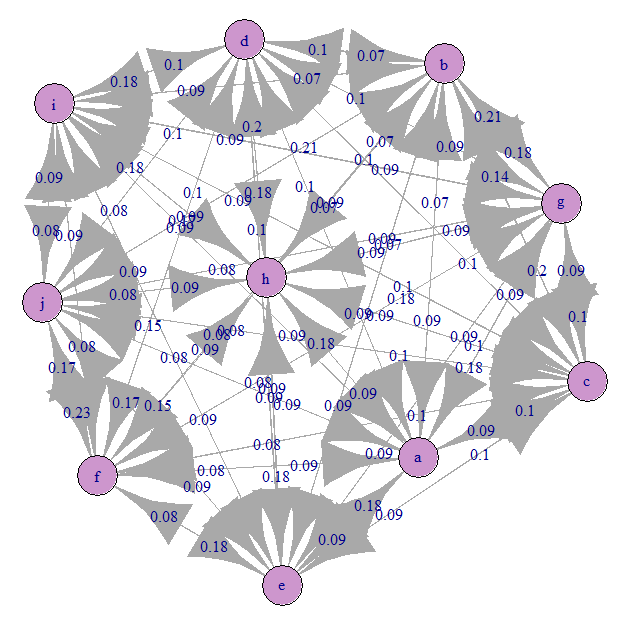
Alles ist ungefähr gleichmäßig verwirrt). Dies liegt daran, dass wir gleichwahrscheinliche Übergänge angegeben haben.

Und jetzt ist die Zeit für Magie!

 ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2)) 

Für eine stochastische Matrix A sollte der erste Eigenwert gleich Eins sein, und der entsprechende Eigenvektor ist der PageRank-Vektor.

> drucken (rund (pr, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11

Dies ist der Vektor der PR-Werte - dies ist der normalisierte Eigenvektor der Übergangsmatrix A, der dem Eigenwert dieser Matrix entspricht, der gleich Eins ist - der dominante Eigenvektor.

Jetzt können Sie die Elemente ordnen. Aufgrund der Besonderheiten des Experiments haben sie jedoch ein sehr ähnliches Gewicht.

Probleme und ihre Lösungen mit der Power-Methode

Die Übergangsmatrix A erfüllt möglicherweise nicht die Stochastizitätsbedingungen.

Erstens kann es Elemente geben, die sich nirgendwo beziehen, dh ohne Feedback (sie können sich selbst auf sie beziehen). Bei großen realen Graphen ist dies ein wahrscheinliches Problem. Dies bedeutet, dass eine der Spalten der Matrix nur Nullen enthält. In diesem Fall funktioniert die Lösung durch Eigenvektoren nicht.

Google hat dieses Problem gelöst, indem eine Spalte mit einer gleichmäßigen Wahrscheinlichkeitsverteilung p = 1 / N ausgefüllt wurde. Wobei N die Anzahl aller Elemente ist.

 dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) 

Zweitens kann das Diagramm Elemente mit gegenseitiger Rückkopplung enthalten, jedoch nicht die verbleibenden Elemente des Diagramms. Dies ist auch ein unüberwindbares Problem für die lineare Algebra aufgrund von Verstößen gegen Annahmen.

Es wird gelöst, indem eine Konstante eingeführt wird, die als Dämpfungsfaktor bezeichnet wird und die a priori Wahrscheinlichkeit eines Übergangs von einem Element zu einem anderen angibt, selbst wenn keine physischen Verbindungen bestehen. Mit anderen Worten ist eine Diffusion in jedem Zustand möglich.

 d = 0.15 #damping factor (to ensure algorithm convergence) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix 

Wenn wir diese Transformationen auf unsere Matrix anwenden, kann sie wieder durch Eigenvektoren gelöst werden!

Drittens ist die abgedroschene Matrix möglicherweise nicht quadratisch, aber dies ist kritisch! Ich werde auf diesen Moment nicht näher eingehen, weil ich glaube, dass Sie selbst herausfinden werden, wie Sie ihn beheben können.

Es gibt jedoch eine schnellere und genauere Methode, die auch im Speicher wirtschaftlicher ist (was für große Diagramme relevant sein kann): die Leistungsmethode.

 ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names 

Voila!

> drucken (rund (pr, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11
> drucken (rund (pr2, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11

Dazu werde ich das Tutorial beenden. Ich hoffe, Sie finden es nützlich.

Ich habe vergessen zu sagen, dass Sie zum Erstellen einer Matrix von Übergängen (Wahrscheinlichkeiten) die Ähnlichkeit von Texten, die Anzahl der Referenzen, die Tatsache eines Links und andere Metriken verwenden können, die zu Pseudowahrscheinlichkeiten führen oder Wahrscheinlichkeiten sind. Ein ziemlich interessantes Beispiel ist die Rangfolge der Sätze im Text in der Ähnlichkeitsmatrix der Wortbeutel tf-idf, um den Satz hervorzuheben, der den gesamten Text zusammenfasst. Es kann andere kreative Verwendungen von PR geben.

Ich empfehle, alleine zu versuchen, mit der Übergangsmatrix zu spielen und sicherzustellen, dass Sie coole PR-Werte erhalten, die auch recht einfach zu interpretieren sind.

Wenn Sie Ungenauigkeiten oder Fehler bei mir sehen - geben Sie dies in den Kommentaren oder in der Nachricht an, und ich werde alles korrigieren.

Der gesamte Code wird hier kompiliert:


PS: Diese ganze Idee lässt sich auch leicht in anderen Sprachen umsetzen, zumindest in Python, ich habe alles ohne Schwierigkeiten gemacht.