Pseudo Lens Flare

Hallo Habr! Ich präsentiere Ihnen die Übersetzung des Artikels „Pseudo Lens Flare“ von John Chapman.



Lens Flare (Lens Flare) ist ein fotografisches Artefakt, das durch Streuung und Brechung von Licht in einem Linsensystem entsteht. Obwohl es sich um ein Artefakt handelt, gibt es viele Gründe, Linseneffekte in Computergrafiken zu verwenden:

• Es erhöht die wahrgenommene Helligkeit und den sichtbaren Dynamikbereich des Bildes.
• Linseneffekte sind häufig auf Fotografien zu finden, so dass ihre Abwesenheit auffällig sein kann
• Es kann eine wichtige Rolle im Stil oder im Drama spielen oder Teil des Gameplays in Spielen sein (stellen Sie sich vor, Blendung macht einen Spieler blind).

Traditionell wurde Lens Flare in Echtzeit mithilfe von Sprite-basierten Technologien implementiert. Obwohl Sprites leicht zu kontrollierende und sehr realistische Ergebnisse liefern, müssen sie explizit platziert werden und erfordern Okklusionsdaten, um korrekt angezeigt zu werden. Hier werde ich einen einfachen und relativ billigen Bildschirmraumeffekt beschreiben, der aus dem Eingabefarbpuffer ein Pseudo- Linseneffekt erzeugt. Es basiert nicht auf Physik, daher unterscheidet sich das Ergebnis geringfügig vom fotorealistischen, es kann jedoch in Kombination mit (oder als Ersatz) herkömmlichen Sprite-basierten Effekten verwendet werden.

Algorithmus

Besteht aus 4 Stufen:

1. Downsample / Schwelle.
2. Erzeugung von Linseneffektelementen .
3. Unschärfe
4. Gehoben / mit dem Originalbild verschmelzen.

1. Downsample / Threshold

Downsampling - Optimierung zur Reduzierung der Kosten nachfolgender Schritte. Außerdem möchten wir eine Teilmenge der hellsten Pixel im Originalbild auswählen. Die Verwendung von Scale / Bias (Scale / Bias) bietet eine flexible Möglichkeit, dies zu erreichen:

uniform sampler2D uInputTex; uniform vec4 uScale; uniform vec4 uBias; noperspective in vec2 vTexcoord; out vec4 fResult; void main() { fResult = max(vec4(0.0), texture(uInputTex, vTexcoord) + uBias) * uScale; } 

Die Einstellung von Skalierung / Bias ist die Hauptmethode zum Anpassen des Effekts. Die besten Einstellungen hängen vom Dynamikbereich des Farbpuffers sowie davon ab, wie dünn das Ergebnis angezeigt werden soll. Aufgrund der Tatsache, dass die Technik eine Annäherung ist, sieht die Subtilität eher besser aus.

2. Erzeugung von Linseneffektelementen

Linseneffektelemente neigen dazu, sich um die Bildmitte zu drehen. Indem wir diesen Effekt simulieren, können wir das Ergebnis der vorherigen Stufe horizontal / vertikal erweitern. Dies ist in der Phase der Elementgenerierung einfach zu tun, indem die Texturkoordinaten erweitert werden:

 vec2 texcoord = -vTexcoords + vec2(1.0); 

Dies ist nicht notwendig; Die Elementgenerierung funktioniert gut mit und ohne. Das Ergebnis der Änderung der Texturkoordinaten hilft jedoch dabei, den Linseneffekt visuell vom Originalbild zu trennen.

Geister

„ Geister “ (Geister) wiederholen Glanzlichter, die die hellen Bereiche im Farbpuffer reflektieren und sich relativ zur Bildmitte entfalten. Der Ansatz, den ich generiert habe, besteht darin, einen Vektor vom aktuellen Pixel in die Mitte des Bildschirms zu bringen und dann mehrere Auswahlen entlang dieses Vektors zu treffen.

 uniform sampler2D uInputTex; uniform int uGhosts; // number of ghost samples uniform float uGhostDispersal; // dispersion factor noperspective in vec2 vTexcoord; out vec4 fResult; void main() { vec2 texcoord = -vTexcoord + vec2(1.0); vec2 texelSize = 1.0 / vec2(textureSize(uInputTex, 0)); // ghost vector to image centre: vec2 ghostVec = (vec2(0.5) - texcoord) * uGhostDispersal; // sample ghosts: vec4 result = vec4(0.0); for (int i = 0; i < uGhosts; ++i) { vec2 offset = fract(texcoord + ghostVec * float(i)); result += texture(uInputTex, offset); } fResult = result; } 

Beachten Sie, dass ich Fract () verwende, um sicherzustellen, dass die Texturkoordinaten umlaufen . Entsprechend können Sie den Wrap-Modus GL_REPEAT für die Textur verwenden.

Hier ist das Ergebnis:



Sie können das Ergebnis verbessern, indem Sie nur helle Bereiche näher an der Bildmitte zulassen, um Geisterbilder zu erzeugen. Wir können dies erreichen, indem wir Gewichte hinzufügen, die von der Mitte für Proben abnehmen:

 vec4 result = vec4(0.0); for (int i = 0; i < uGhosts; ++i) { vec2 offset = fract(texcoord + ghostVec * float(i)); float weight = length(vec2(0.5) - offset) / length(vec2(0.5)); weight = pow(1.0 - weight, 10.0); result += texture(uInputTex, offset) * weight; } 

Die Gewichtsfunktion ist so einfach wie möglich - linear. Der Grund, warum wir das Gewicht innerhalb der Schleife berechnen, ist, dass die hellen Bereiche in der Mitte des Eingabebilds Geister in die Ränder „werfen“ können, die hellen Bereiche an den Rändern jedoch keine Geister in die Mitte werfen können.



Die letzte Verbesserung ist die radiale Farbänderung des Geistes gemäß der 1D-Textur:



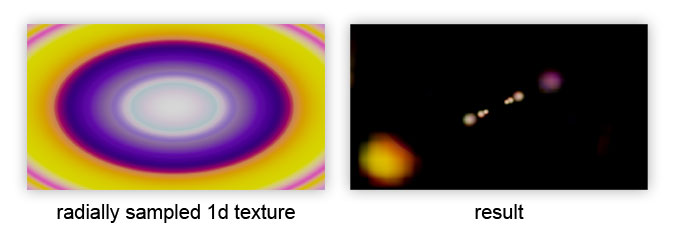
Es wird nach dem Zyklus angewendet, um die endgültige Farbe des Geistes zu beeinflussen:

 result *= texture(uLensColor, length(vec2(0.5) - texcoord) / length(vec2(0.5))); 

Halos (Lichthöfe)

Wenn wir den Vektor wie bei der Geisterberechnung in die Bildmitte bringen, aber die Länge des Vektors festlegen, erhalten wir einen weiteren Effekt: Das Originalbild wird radial deformiert:


Wir können dies verwenden, um einen „Lichthof“ zu erzeugen, indem wir das Gewicht mit einer Probe multiplizieren und dadurch den Beitrag des deformierten Bildes zu einem Ring begrenzen, dessen Radius von uHaloWidth gesteuert wird:

 // sample halo: vec2 haloVec = normalize(ghostVec) * uHaloWidth; float weight = length(vec2(0.5) - fract(texcoord + haloVec)) / length(vec2(0.5)); weight = pow(1.0 - weight, 5.0); result += texture(uInputTex, texcoord + haloVec) * weight; 

CHROMATISCHE VERZERRUNG (Farbverzerrung)

Einige Linseneffekte weisen Farbverzerrungen auf, die durch Variationen der Lichtbrechung bei verschiedenen Wellenlängen verursacht werden. Wir können dies simulieren, indem wir eine Funktion erstellen, die die roten, grünen und blauen Kanäle separat mit leicht unterschiedlichen Offsets entlang des Stichprobenvektors auswählt:

 vec3 textureDistorted( in sampler2D tex, in vec2 texcoord, in vec2 direction, // direction of distortion in vec3 distortion // per-channel distortion factor ) { return vec3( texture(tex, texcoord + direction * distortion.r).r, texture(tex, texcoord + direction * distortion.g).g, texture(tex, texcoord + direction * distortion.b).b ); } 

Es kann als direkter Ersatz für den Aufruf von textur () in der vorherigen Liste verwendet werden. Ich berechne Richtung und Verzerrung wie folgt:

 vec2 texelSize = 1.0 / vec2(textureSize(uInputTex, 0)); vec3 distortion = vec3(-texelSize.x * uDistortion, 0.0, texelSize.x * uDistortion); vec3 direction = normalize(ghostVec); 

Obwohl die Abruffunktion einfach ist, kostet sie x3 Samples aus der Textur, obwohl sie alle cachefreundlich sein sollten, es sei denn, Sie setzen uDistortion auf einen gigantischen Wert.

Mit der Erzeugung von Elementen alles. Hier ist das Ergebnis:

3. Verwischen

Ohne Unschärfe neigen Linseneffektelemente (insbesondere Geister) dazu, das Erscheinungsbild des Bildes beizubehalten. Durch Hinzufügen von Unschärfe zu den Linseneffektelementen werden die hohen Frequenzen geschwächt und dadurch der Kontrast zum Eingabebild verringert, wodurch wir den Effekt verkaufen können.



Ich werde nicht sagen, wie man eine Unschärfe macht; Sie können darüber in verschiedenen Internetquellen lesen (Gaußsche Unschärfe).

4. Erhöhen / mischen Sie mit dem Originalbild

Wir haben also unsere Linseneffektelemente gut verschwommen. Wie können wir sie mit dem ursprünglichen Quellbild kombinieren? Es gibt mehrere wichtige Überlegungen zur gesamten Render-Pipeline:

• Nachfolgende Bewegungsunschärfe oder Schärfentiefe müssen vor dem Kombinieren mit Linseneffekt angewendet werden, damit Linseneffektelemente nicht an diesen Effekten beteiligt sind.
• Vor jeder Tonabbildung sollte ein Linseneffekt angewendet werden . Dies ist physikalisch sinnvoll, da Tonemapping die Film- / CMOS-Reaktion auf einfallendes Licht nachahmt, wobei Linseneffekt ein wesentlicher Bestandteil ist.

Vor diesem Hintergrund können wir in dieser Phase einige Maßnahmen ergreifen, um das Ergebnis zu verbessern:

LENS DIRT

Zuerst müssen Sie die Linseneffektelemente mit einer schmutzigen Textur in voller Auflösung modifizieren (was in Battlefield 3 weit verbreitet ist):

 uniform sampler2D uInputTex; // source image uniform sampler2D uLensFlareTex; // input from the blur stage uniform sampler2D uLensDirtTex; // full resolution dirt texture noperspective in vec2 vTexcoord; out vec4 fResult; void main() { vec4 lensMod = texture(uLensDirtTex, vTexcoord); vec4 lensFlare = texture(uLensFlareTex, vTexcoord) * lensMod; fResult = texture(uInputTex, vTexcoord) + lensflare; } 

Der Schlüssel dazu ist die sehr schmutzige Textur auf den Linsen. Wenn der Kontrast gering ist, dominieren Linseneffektformen tendenziell das Ergebnis. Mit zunehmendem Kontrast werden die Linseneffektelemente gedämpft, was ein anderes ästhetisches Erscheinungsbild ergibt und auch einige Mängel verbirgt.

DIFFRAKTION STARBURST

Als zusätzliche Verbesserung können wir die Starburst- Textur verwenden, indem wir sie dem Linsenschmutz hinzufügen:


Als Textur sieht Starburst nicht sehr gut aus. Trotzdem können wir die Transformationsmatrix an den Shader übergeben, wodurch wir den Starburst in jedem Frame drehen / deformieren und den gewünschten dynamischen Effekt erzielen können:

 uniform sampler2D uInputTex; // source image uniform sampler2D uLensFlareTex; // input from the blur stage uniform sampler2D uLensDirtTex; // full resolution dirt texture uniform sampler2D uLensStarTex; // diffraction starburst texture uniform mat3 uLensStarMatrix; // transforms texcoords noperspective in vec2 vTexcoord; out vec4 fResult; void main() { vec4 lensMod = texture(uLensDirtTex, vTexcoord); vec2 lensStarTexcoord = (uLensStarMatrix * vec3(vTexcoord, 1.0)).xy; lensMod += texture(uLensStarTex, lensStarTexcoord); vec4 lensFlare = texture(uLensFlareTex, vTexcoord) * lensMod; fResult = texture(uInputTex, vTexcoord) + lensflare; } 

Die uLensStarMatrix- Transformationsmatrix basiert auf dem Wert, der aus der Kameraausrichtung wie folgt erhalten wird:

 vec3 camx = cam.getViewMatrix().col(0); // camera x (left) vector vec3 camz = cam.getViewMatrix().col(1); // camera z (forward) vector float camrot = dot(camx, vec3(0,0,1)) + dot(camz, vec3(0,1,0)); 

Es gibt andere Möglichkeiten, den Camrot-Wert zu ermitteln. Am wichtigsten ist, dass es sich kontinuierlich ändert, wenn die Kamera gedreht wird. Die Matrix selbst ist wie folgt aufgebaut:

 mat3 scaleBias1 = ( 2.0f, 0.0f, -1.0f, 0.0f, 2.0f, -1.0f, 0.0f, 0.0f, 1.0f, ); mat3 rotation = ( cos(camrot), -sin(camrot), 0.0f, sin(camrot), cos(camrot), 0.0f, 0.0f, 0.0f, 1.0f ); mat3 scaleBias2 = ( 0.5f, 0.0f, 0.5f, 0.0f, 0.5f, 0.5f, 0.0f, 0.0f, 1.0f, ); mat3 uLensStarMatrix = scaleBias2 * rotation * scaleBias1; 

Skalierungs- und Bias- Matrizen benötigen Texturursprungsversätze, damit wir den Starburst relativ zur Bildmitte drehen können.

Fazit

Also jetzt alles! Diese Methode zeigt, wie ein relativ vereinfachter Nachbearbeitungsprozess zu einem anständig aussehenden Linseneffekt führt . Es ist nicht vollständig fotorealistisch, kann aber bei richtiger Anwendung hervorragende Ergebnisse erzielen.