Wie ist der Barcode angeordnet?

Hallo Habr!

Ein moderner Mensch trifft jeden Tag auf Barcodes, ohne darüber nachzudenken. Wenn wir Produkte im Supermarkt kaufen, werden deren Codes mit Hilfe eines Barcodes genau gelesen. Auch Pakete, Waren in Lagern und so weiter und so fort. Allerdings wissen nur wenige, wie es wirklich funktioniert.

Wie ist der Barcode angeordnet und was ist in diesem Bild codiert?



Versuchen wir es herauszufinden, gleichzeitig schreiben wir einen Decoder für solche Codes.

Einführung

Die Verwendung von Barcodes hat eine lange Geschichte. Die ersten Automatisierungsversuche begannen bereits in den 1950er Jahren, 1952 wurde ein Patent für einen Codeleser erteilt. Der an der Sortierung der Waggons auf der Eisenbahn beteiligte Ingenieur wollte den Prozess vereinfachen. Die Idee war offensichtlich - die Nummer mit Streifen zu codieren und sie mit Fotozellen zu lesen. 1962 wurden Codes offiziell zur Identifizierung von Autos auf der amerikanischen Eisenbahn ( KarTrak- System) verwendet. 1968 wurde der Suchscheinwerfer durch einen Laserstrahl ersetzt, der die Genauigkeit erhöhte und die Größe des Lesegeräts verringerte. 1973 erschien das Format „Universal Product Code“, und 1974 wurde das erste Produkt mit einem Codescanner (Wrigleys Kaugummi sind die USA;) in einem Supermarkt verkauft. 1984 verwendete ein Drittel der Geschäfte Luftschlangen, aber in Russland wurden sie um die 90er Jahre verwendet.

Es werden sehr viele verschiedene Codes für verschiedene Aufgaben verwendet, zum Beispiel kann die Sequenz „12345678“ auf diese Weise dargestellt werden (und das ist noch nicht alles):



Beginnen wir mit dem bitweisen Parsen. Darüber hinaus bezieht sich alles, was unten beschrieben wird, auf das Formular „Code-128“ - einfach, weil sein Format recht einfach und unkompliziert ist. Wer mit anderen Arten experimentieren möchte, kann einen Online-Generator öffnen und sich selbst davon überzeugen.

Auf den ersten Blick scheint der Barcode nur eine zufällige Folge von Zeilen zu sein, tatsächlich ist seine Struktur klar festgelegt:



1 - Leerer Speicherplatz zur eindeutigen Identifizierung des Codeanfangs
2 - Startsymbol. Für Code-128 sind 3 Optionen möglich (A, B und C genannt): 11010000100, 11010010000 oder 11010011100, sie entsprechen verschiedenen Codetabellen (weitere Einzelheiten siehe Wikipedia ).
3 - Eigentlich der Code, der die Daten enthält, die wir brauchen
4 - Prüfsumme
5 - Stoppsymbol. Für Code-128 ist dies 1100011101011.
6 (1) - Leerraum.

Nun dazu, wie Bits codiert werden. Hier ist alles sehr einfach - wenn Sie die Breite der dünnsten Linie als „1“ annehmen, gibt die Linie mit doppelter Breite den Code „11“, ein dreifaches „111“ usw. an. Der leere Raum ist nach dem gleichen Prinzip "0" oder "00" oder "000". Wer möchte, kann den Startcode im Bild vergleichen, um sicherzustellen, dass die Regel erfüllt ist.

Jetzt können Sie mit der Programmierung beginnen.

Holen Sie sich die Bitfolge

Im Prinzip ist dies der schwierigste Teil, und natürlich kann er algorithmisch auf verschiedene Arten implementiert werden. Ich bin mir nicht sicher, ob der folgende Algorithmus optimal ist, aber für eine Fallstudie reicht er völlig aus.

Laden Sie zunächst das Bild, dehnen Sie es in der Breite, ziehen Sie eine horizontale Linie von der Bildmitte, konvertieren Sie es in s / w und laden Sie es als Array.

from PIL import Image import numpy as np import matplotlib.pyplot as plt image_path = "barcode.jpg" img = Image.open(image_path) width, height = img.size basewidth = 4*width img = img.resize((basewidth, height), Image.ANTIALIAS) hor_line_bw = img.crop((0, int(height/2), basewidth, int(height/2) + 1)).convert('L') hor_data = np.asarray(hor_line_bw, dtype="int32")[0] 

Auf dem Barcode entspricht „1“ Schwarz und auf RGB dagegen 0, daher muss das Array invertiert werden. Gleichzeitig berechnen wir den Durchschnittswert.

 hor_data = 255 - hor_data avg = np.average(hor_data) plt.plot(hor_data) plt.show() 

Wir starten das Programm, um sicherzustellen, dass der Barcode korrekt geladen ist:



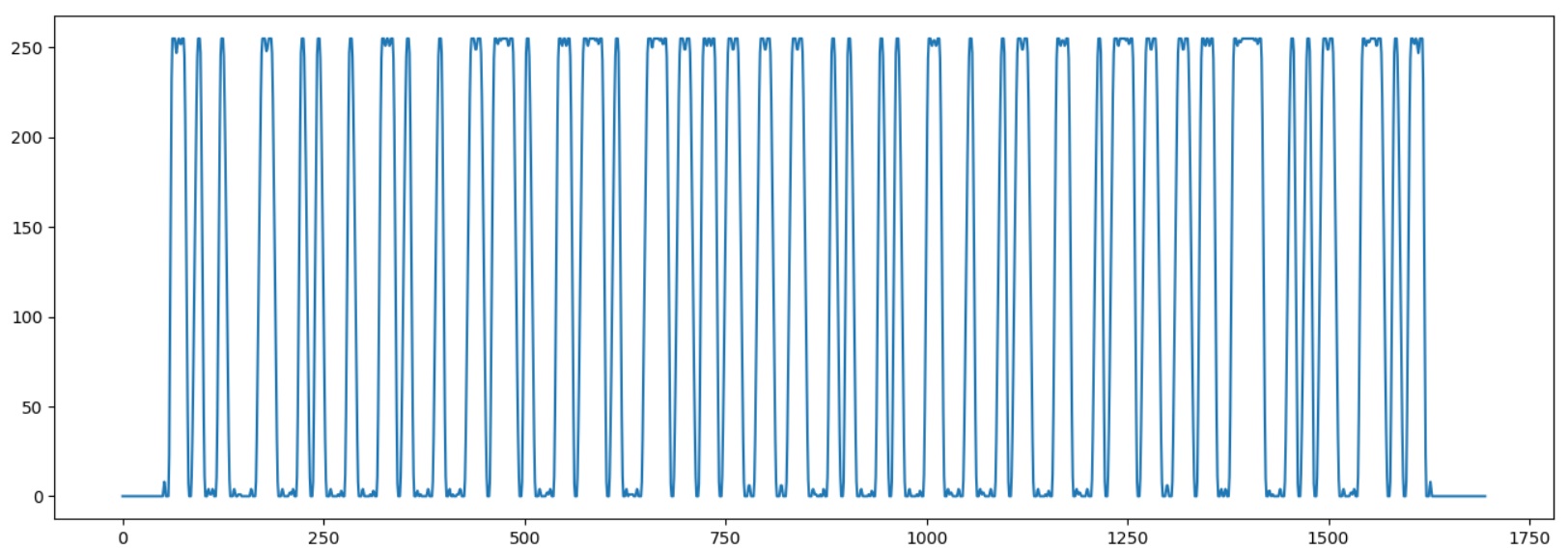
Jetzt müssen Sie die Breite eines "Bits" bestimmen. Dazu markieren wir den Beginn der Startsequenz "1101" und zeichnen die Momente des Übergangs des Graphen durch die Mittellinie auf.

 pos1, pos2 = -1, -1 bits = "" for p in range(basewidth - 2): if hor_data[p] < avg and hor_data[p + 1] > avg: bits += "1" if pos1 == -1: pos1 = p if bits == "101": pos2 = p break if hor_data[p] > avg and hor_data[p + 1] < avg: bits += "0" bit_width = int((pos2 - pos1)/3) 

Wir zeichnen nur die Übergänge durch die Mitte auf, so dass der Code „1101“ als „101“ geschrieben wird. Dies reicht jedoch aus, um die Breite in Pixel zu ermitteln.

Nun die eigentliche Dekodierung. Wir finden den nächsten Übergang durch die Mitte und bestimmen die Anzahl der Bits, die in das Intervall fallen. Da die Übereinstimmung nicht absolut ist (der Code kann leicht gekrümmt oder gedehnt sein), verwenden wir die Rundung.

 bits = "" for p in range(basewidth - 2): if hor_data[p] > avg and hor_data[p + 1] < avg: interval = p - pos1 cnt = interval/bit_width bits += "1"*int(round(cnt)) pos1 = p if hor_data[p] < avg and hor_data[p + 1] > avg: interval = p - pos1 cnt = interval/bit_width bits += "0"*int(round(cnt)) pos1 = p 

Ich bin mir nicht sicher, ob dies die beste Option ist. Vielleicht gibt es einen besseren Weg. Diejenigen, die dies wünschen, können in die Kommentare schreiben.

Wenn alles richtig gemacht wurde, erhalten wir ungefähr die folgende Reihenfolge der Ausgabe:

11010010000110001010001000110100010001101110100011011101000111011011
01100110011000101000101000110001000101100011000101110110011011001111
00010101100011101011

Dekodierung

Hier gibt es grundsätzlich keine Schwierigkeiten. Zeichen in Code-128 werden mit einem 11-Bit-Code codiert, der 3 Varianten (A, B und C) aufweist und entweder unterschiedliche Zeichencodierungen oder Zahlen von 00 bis 99 speichern kann.

In unserem Fall ist der Beginn der Sequenz 11010010000, was „Code B“ entspricht. Es war furchtbar kaputt, alle Codes aus Wikipedia manuell einzugeben, daher wurde die Tabelle einfach aus dem Browser kopiert und auch in Python analysiert (Hinweis: Dies ist für die Produktion nicht erforderlich).

  CODE128_CHART = """ 0 _ _ 00 32 S 11011001100 212222 1 ! ! 01 33 ! 11001101100 222122 2 " " 02 34 " 11001100110 222221 3 # # 03 35 # 10010011000 121223 ... 93 GS } 93 125 } 10100011110 111341 94 RS ~ 94 126 ~ 10001011110 131141 103 Start Start A 208 SCA 11010000100 211412 104 Start Start B 209 SCB 11010010000 211214 105 Start Start C 210 SCC 11010011100 211232 106 Stop Stop - - - 11000111010 233111""".split() SYMBOLS = [value for value in CODE128_CHART[6::8]] VALUESB = [value for value in CODE128_CHART[2::8]] CODE128B = dict(zip(SYMBOLS, VALUESB)) 

Jetzt bleibt das Einfachste. Wir teilen unsere Bitfolge in Blöcke mit 11 Zeichen auf:

 sym_len = 11 symbols = [bits[i:i+sym_len] for i in range(0, len(bits), sym_len)] 

Schließlich bilden wir die Linie und zeigen sie auf dem Bildschirm an:

 str_out = "" for sym in symbols: if CODE128A[sym] == 'Start': continue if CODE128A[sym] == 'Stop': break str_out += CODE128A[sym] print(" ", sym, CODE128A[sym]) print("Str:", str_out) 

Ich werde keine Antwort auf das geben, was in der Tabelle verschlüsselt ist. Lassen Sie es eine Hausaufgabe für die Leser sein (die Verwendung von vorgefertigten Programmen für Smartphones wird als Betrug betrachtet :).

Der Code implementiert auch keine CRC-Überprüfung, diejenigen, die dies wünschen, können dies selbst tun.

Natürlich ist der Algorithmus nicht perfekt und wurde in einer halben Stunde geschrieben. Für professionellere Zwecke gibt es vorgefertigte Bibliotheken, zum Beispiel pyzbar . Code, der eine solche Bibliothek verwendet, benötigt nur 4 Zeilen:

 from pyzbar.pyzbar import decode img = Image.open(image_path) decode = decode(img) print(decode) 

(Zuerst müssen Sie die Bibliothek installieren, indem Sie den Befehl pip install pyzbar eingeben.)

Ergänzung : vinograd19 schrieb in den Kommentaren zur CRC-Zählung:

Die Geschichte der Prüfziffer ist interessant. Es entstand evolutionär.
Die Prüfziffer wird benötigt, um eine fehlerhafte Dekodierung zu vermeiden. Wenn der Barcode 1234 war und als 7234 erkannt wurde, benötigen Sie eine Validierung, die das Ersetzen von 1 durch 7 verhindert. Die Validierung ist möglicherweise ungenau, sodass mindestens 90% der ungültigen Zahlen im Voraus ermittelt werden.

1. Ansatz: Nehmen wir einfach den Betrag. Damit der Rest der Division durch 10 0 ist. Nun, das heißt, die ersten 12 Zeichen tragen eine Informationslast, und die letzte Ziffer wird so ausgewählt, dass die Summe der Ziffern durch 10 geteilt wird. Dekodieren Sie die Sequenz. Wenn die Summe nicht durch 10 teilbar ist, bedeutet dies, dass Sie mit einem Fehler dekodiert haben und dies tun müssen diesmal noch einmal. Beispielsweise ist der Code 1234 gültig. 1 + 2 + 3 + 4 = 10. Code 1216 ist ebenfalls gültig, 1218 jedoch nicht.

Dies vermeidet Probleme mit der Automatisierung. Zum Zeitpunkt der Erstellung der Barcodes gab es jedoch einen Fallback in Form der Eingabe einer Zahl auf den Tasten. Und es gibt einen schlechten Fall: Wenn Sie die Reihenfolge der beiden Ziffern ändern, ändert sich die Prüfsumme nicht, und das ist schlecht. Das heißt, wenn der Barcode 1234 als 2134 gehämmert wurde, konvergiert die Prüfsumme, aber wir haben die falsche Nummer eingegeben. Es stellt sich heraus, dass die falsche Reihenfolge der Zahlen häufig vorkommt, wenn Sie schnell auf die Tasten klopfen.

2. Ansatz. Lassen Sie uns die Menge etwas komplizierter machen. Damit werden die Zahlen an geraden Stellen zweimal berücksichtigt. Wenn Sie dann die Reihenfolge ändern, konvergiert der Betrag definitiv nicht zum gewünschten. Beispielsweise ist Code 2364 gültig (2 + 3 + 3 + 6 + 4 + 4 = 20) und Code 3264 ist ungültig (3+ 2 + 2 + 6 + 4 + 4 = 19). Aber hier war ein anderes schlechtes Beispiel für das Fahren. Einige Tastaturen sind so angeordnet, dass zehn Ziffern in zwei Reihen angeordnet sind. Die erste Zeile ist 12345 und darunter die zweite zweite Zeile 67890. Wenn Sie anstelle der Taste „1“ die Taste „2“ rechts drücken, verhindert die Prüfsumme eine falsche Eingabe. Wenn Sie jedoch anstelle der Taste „1“ die unten stehende Taste „6“ drücken, wird möglicherweise keine Warnung ausgegeben. Immerhin ist 6 = 1 + 5, und wenn diese Zahl bei der Berechnung der Prüfsumme an einer geraden Stelle liegt, haben wir 2 * 6 = 2 * 1 + 2 * 5. Das heißt, die Prüfsumme wurde um genau 10 erhöht, sodass sich die letzte Ziffer nicht geändert hat. Beispielsweise sind die Prüfsummen in den Codes 2134 und 2634 gleich. Der gleiche Fehler tritt auf, wenn wir 7 statt 2 drücken, statt 3 8 drücken und so weiter.

3. Ansatz. Ok, nehmen wir die Summe noch einmal, nur die Zahlen an geraden Stellen werden berücksichtigt ... dreimal. Das heißt, der Code 1234565 ist gültig, da 1 + 2 * 3 + 3 + 4 * 3 + 5 + 6 * 3 + 5 = 50.

Die beschriebene Methode ist zum Standard für die Berechnung der EAN13-Prüfsumme mit einigen Korrekturen geworden: Die Anzahl der Ziffern ist fest und gleich 13, wobei die 13. die gleiche Prüfsumme ist. Die Zahlen an ungeraden Stellen werden dreimal gezählt, an geraden einmal.

Fazit

Wie Sie sehen können, enthält selbst eine so einfache Sache wie ein Barcode viele interessante Dinge. Übrigens, ein weiterer Life-Hack für diejenigen, die bis hierher gelesen haben - der Text unter dem Barcode (falls vorhanden) dupliziert seinen Inhalt vollständig. Dies geschieht, damit der Bediener den unlesbaren Code manuell eingeben kann. Um den Inhalt eines Barcodes herauszufinden, ist es normalerweise einfach - schauen Sie sich einfach den Text darunter an.

Wie in den Kommentaren vorgeschlagen, ist der EAN-13-Code im Handel am beliebtesten, die Bitcodierung ist dort dieselbe, und diejenigen, die dies wünschen, können die Zeichenstruktur selbst sehen .

Wenn die Leser das Interesse nicht verloren haben, können Sie QR-Codes separat berücksichtigen.

Vielen Dank für Ihre Aufmerksamkeit.