Wie funktioniert ein Barcode?

Hallo zusammen!

Jeder Mensch benutzt heutzutage Barcodes, meistens ohne es zu merken. Wenn wir die Lebensmittel im Geschäft kaufen, werden ihre Kennungen von Barcodes abgerufen. Das Gleiche gilt auch für Waren in den Lagern, Postpaketen und so weiter. Aber nicht so viele Leute wissen tatsächlich, wie es funktioniert.

Was befindet sich im Barcode und was ist auf diesem Bild codiert?



Lass es uns herausfinden und lass uns auch unseren eigenen Bardecoder schreiben.

Einführung

Die Verwendung von Barcodes hat eine lange Geschichte. Erste Versuche zur Automatisierung wurden in den 50er Jahren unternommen, das Patent für ein Code-Lesesystem wurde erteilt. David Collins, der bei der Pennsylvania Railroad arbeitete, beschloss, den Sortiervorgang für Autos zu vereinfachen. Die Idee lag auf der Hand: Die Fahrzeugkennungen mit verschiedenen Farbstreifen zu codieren und mit einer Fotozelle zu lesen. 1962 wurde ein solcher Code von der Association of American Railroads zum Standard. (das KarTrak- System). 1968 wurde die Lampe durch einen Laser ersetzt, wodurch die Genauigkeit erhöht und die Lesegröße verringert werden konnte. 1973 wurde der Universal Product Code entwickelt und 1974 das erste Lebensmittelprodukt (ein Wrigley-Kaugummi - es war offensichtlich in den USA;) verkauft. Im Jahr 1984 hat der dritte Teil aller Geschäfte Barcodes verwendet, in anderen Ländern wurde es später populär.

Es gibt viele verschiedene Barcode-Typen für verschiedene Anwendungen. Beispielsweise kann die Zeichenfolge "12345678" auf diese Weise codiert werden (und es sind nicht alle):



Beginnen wir mit der Analyse. Alle folgenden Informationen beziehen sich auf den Typ "Code-128" - nur weil das Prinzip leicht zu verstehen ist. Wer andere Modi testen möchte, kann den Online-Barcode-Generator verwenden und andere Typen selbst testen.

Auf den ersten Blick sieht ein Barcode wie eine zufällige Reihe von Zahlen aus, aber tatsächlich ist seine Struktur gut organisiert:



1 - Leerer Platz, der zur Bestimmung der Code-Startposition erforderlich ist.
2 - Startsymbol. Es stehen drei Arten von Code-128 zur Verfügung (A, B und C genannt), und Startsymbole können 11010000100, 11010010000 bzw. 11010011100 sein. Bei diesen Typen unterscheiden sich die Codierungstabellen ( weitere Informationen finden Sie in der Beschreibung von Code_128 ).
3 - Der Code selbst, der Benutzerdaten enthält.
4 - Prüfsumme.
5 - Stoppsymbol für Code-128 1100011101011.
6 (1) - Leerraum.

Schauen wir uns nun an, wie die Bits codieren. Es ist wirklich einfach - wenn wir die dünnste Linienbreite auf "1" setzen, dann ist die Linie mit doppelter Breite "11", die Linie mit dreifacher Breite ist "111" und so weiter. Der leere Raum wird nach dem gleichen Prinzip jeweils "0", "00" oder "000" sein. Interessenten können die Startsequenz auf dem Bild oben vergleichen, um festzustellen, ob die Regel eingehalten wird.

Jetzt können wir mit dem Codieren beginnen.

Abrufen der Bitfolge

Im Allgemeinen ist es der komplizierteste Teil, und es kann auf verschiedene Arten durchgeführt werden. Ich bin mir nicht sicher, ob mein Ansatz optimal ist, aber für unsere Aufgabe ist es definitiv genug.

Lassen Sie uns zunächst das Bild laden, seine Breite dehnen, eine horizontale Linie von der Mitte aus zuschneiden, es in eine s / w-Farbe konvertieren und als Array speichern.

from PIL import Image import numpy as np import matplotlib.pyplot as plt image_path = "barcode.jpg" img = Image.open(image_path) width, height = img.size basewidth = 4*width img = img.resize((basewidth, height), Image.ANTIALIAS) hor_line_bw = img.crop((0, int(height/2), basewidth, int(height/2) + 1)).convert('L') hor_data = np.asarray(hor_line_bw, dtype="int32")[0] 

Auf dem Barcode entspricht die schwarze Linie „1“, aber in RGB ist das Schwarz im Gegensatz zu 0, sodass das Array invertiert werden muss. Wir werden auch den Durchschnittswert berechnen.

 hor_data = 255 - hor_data avg = np.average(hor_data) plt.plot(hor_data) plt.show() 

Führen Sie das Programm aus, um zu überprüfen, ob der Barcode korrekt geladen wurde:



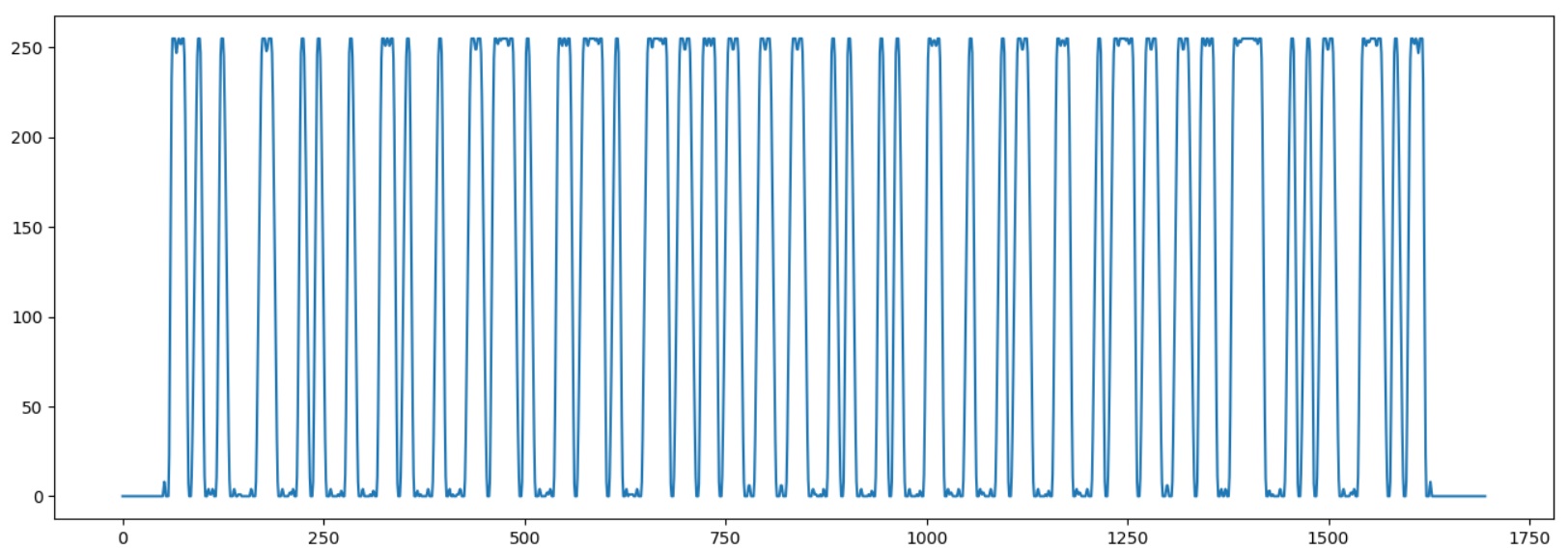
Jetzt müssen wir eine Breite von einem 'Bit' bestimmen. Dazu extrahieren wir die Sequenz und speichern die Positionen der durchschnittlichen Linienkreuzung.

 pos1, pos2 = -1, -1 bits = "" for p in range(basewidth - 2): if hor_data[p] < avg and hor_data[p + 1] > avg: bits += "1" if pos1 == -1: pos1 = p if bits == "101": pos2 = p break if hor_data[p] > avg and hor_data[p + 1] < avg: bits += "0" bit_width = int((pos2 - pos1)/3) 

Wir speichern nur die durchschnittlichen Linienkreuzungen, daher wird der Code "1101" als "101" gespeichert, aber es reicht aus, um die Pixelbreite zu erhalten.

Lassen Sie uns nun die Dekodierung selbst vornehmen. Wir müssen jede durchschnittliche Linienkreuzung finden und die Anzahl der Bits im letzten gefundenen Intervall ermitteln. Die Zahlen stimmen nicht perfekt überein (der Code kann etwas gedehnt oder gebogen werden), daher müssen wir den Wert auf eine Ganzzahl runden.

 bits = "" for p in range(basewidth - 2): if hor_data[p] > avg and hor_data[p + 1] < avg: interval = p - pos1 cnt = interval/bit_width bits += "1"*int(round(cnt)) pos1 = p if hor_data[p] < avg and hor_data[p + 1] > avg: interval = p - pos1 cnt = interval/bit_width bits += "0"*int(round(cnt)) pos1 = p 

Vielleicht gibt es einen besseren Weg, dies zu tun, Leser können in Kommentaren schreiben.

Wenn alles perfekt gemacht wurde, erhalten wir eine Sequenz wie folgt:

11010010000110001010001000110100010001101110100011011101000111011011
01100110011000101000101000110001000101100011000101110110011011001111
00010101100011101011

Dekodierung

Im Allgemeinen ist es ziemlich einfach. Symbole im Code-128 werden mit 11-Bit-Code codiert, der unterschiedliche Codierungen haben kann (gemäß dieser Codierung - A, B oder C können es Buchstaben oder Ziffern von 00 bis 99 sein).

In unserem Fall ist der Beginn der Sequenz 11010010000, was einem "Code B" entspricht. Ich war zu faul, um alle Codes manuell einzugeben, also habe ich sie einfach von einer Wikipedia-Seite kopiert. Das Parsen dieser Zeilen wurde auch in Python durchgeführt (Hinweis - machen Sie solche Dinge nicht in der Produktion).

  CODE128_CHART = """ 0 _ _ 00 32 S 11011001100 212222 1 ! ! 01 33 ! 11001101100 222122 2 " " 02 34 " 11001100110 222221 3 # # 03 35 # 10010011000 121223 ... 93 GS } 93 125 } 10100011110 111341 94 RS ~ 94 126 ~ 10001011110 131141 103 Start Start A 208 SCA 11010000100 211412 104 Start Start B 209 SCB 11010010000 211214 105 Start Start C 210 SCC 11010011100 211232 106 Stop Stop - - - 11000111010 233111""".split() SYMBOLS = [value for value in CODE128_CHART[6::8]] VALUESB = [value for value in CODE128_CHART[2::8]] CODE128B = dict(zip(SYMBOLS, VALUESB)) 

Die letzten Teile sind einfach. Lassen Sie uns zunächst die Sequenz in 11-Bit-Blöcke aufteilen:

 sym_len = 11 symbols = [bits[i:i+sym_len] for i in range(0, len(bits), sym_len)] 

Lassen Sie uns abschließend die Ausgabezeichenfolge generieren und anzeigen:

 str_out = "" for sym in symbols: if CODE128A[sym] == 'Start': continue if CODE128A[sym] == 'Stop': break str_out += CODE128A[sym] print(" ", sym, CODE128A[sym]) print("Str:", str_out) 

Ich werde hier nicht das dekodierte Ergebnis aus dem oberen Bild zeigen, es sei die Hausaufgabe für die Leser (die Verwendung der heruntergeladenen Apps für Smartphones wird als Betrug betrachtet :).

Die CRC-Prüfung ist in diesem Code nicht implementiert. Wer dies möchte, kann dies selbst tun.

Sicher ist dieser Algorithmus nicht perfekt, er wurde in einer halben Stunde erstellt. Für professionelle Aufgaben gibt es gebrauchsfertige Bibliotheken, zum Beispiel pyzbar . Zum Dekodieren des Bildes reichen 4 Codezeilen aus:

 from pyzbar.pyzbar import decode img = Image.open(image_path) decode = decode(img) print(decode) 

(Zuerst muss die Bibliothek mit dem Befehl "pip install pyzbar" installiert werden.)

Ergänzung : Der Site-Benutzer vinograd19 hat einen interessanten Kommentar zum Berechnungsverlauf der Barcode- Prüfsumme gesendet.

Die Berechnung der Schecknummer ist interessant, sie entstand evolutionär.
Eine Prüfsumme wird offensichtlich benötigt, um eine falsche Dekodierung zu vermeiden. Wenn der Barcode 1234 war und als 7234 dekodiert wurde, benötigen wir eine Methode, um das Ersetzen von 1 bis 7 abzulehnen. Die Validierung kann nicht perfekt sein, aber mindestens 90% der Codes sollten korrekt überprüft werden.

1. Ansatz: Nehmen wir einfach die Summe, um 0 als Rest der Division zu haben. Das erste Symbol enthält Daten, und die letzte Ziffer ist so, dass die Summe aller Zahlen durch 10 geteilt wird. Wenn der Betrag nach der Decodierung nicht durch 10 teilbar ist, ist die Decodierung falsch und muss wiederholt werden. Beispielsweise ist der Code 1234 gültig - 1 + 2 + 3 + 4 = 10. Code 1216 - ist ebenfalls gültig, 1218 jedoch nicht.

Dies hilft, Dekodierungsprobleme zu vermeiden. Die Codes können aber auch manuell über die Hardwaretastatur eingegeben werden. Auf diese Weise wurde ein weiterer schlechter Fall gefunden - wenn die Reihenfolge der zwei Ziffern geändert wird, ist die Prüfsumme immer noch korrekt, es ist definitiv schlecht. Wenn beispielsweise der Barcode 1234 als 2134 eingegeben wurde, ist die Prüfsumme dieselbe. Es wurde festgestellt, dass eine falsche Ziffernreihenfolge häufig vorkommt, wenn eine Person versucht, Ziffern schnell einzugeben.

2. Ansatz. Verbessern wir den Prüfsummenalgorithmus - lassen Sie uns die ungeraden Zahlen zweimal berechnen. Wenn dann die Reihenfolge geändert wird, ist die Summe falsch. Beispielsweise ist der Code 2364 gültig (2 + 3 * 2 + 6 + 4 * 2 = 20), der Code 3264 jedoch nicht (3 + 2 * 2 + 6 + 4 * 2 = 19). Es ist besser, aber ein anderer Fall ist aufgetreten. Es gibt einige Tastaturen mit 10 Tasten in zwei Zeilen, die erste Zeile ist 12345 und die zweite ist 67890. Wenn der Benutzer anstelle von "1" "2" eingibt, schlägt die Prüfsummenprüfung fehl. Wenn der Benutzer jedoch "6" anstelle von "1" eingibt, kann die Prüfsumme manchmal korrekt sein. Dies liegt daran, dass 6 = 1 + 5 ist und wenn die Ziffer eine ungerade Stelle hat, 2 * 6 = 2 * 1 + 2 * 5 - die Summe hat sich um 10 erhöht. Der gleiche Fehler tritt auf, wenn der Benutzer "7" eingibt "Anstelle von" 2 "," 8 "anstelle von" 3 "und so weiter.

3. Ansatz. Nehmen wir die Summe noch einmal, aber lassen Sie uns ungerade Zahlen erhalten ... 3 mal. Zum Beispiel ist der Code 1234565 - gültig, weil 1 + 2 * 3 + 3 + 4 * 3 + 5 + 6 * 3 + 5 = 50.

Diese Methode wurde mit einigen Änderungen zum Standard für EAN13-Code: Die Anzahl der Ziffern ist fest und gleich 13, wobei die 13. Ziffer - die Prüfsumme ist. Zahlen an ungeraden Stellen werden dreimal gezählt, an geraden Stellen einmal.

Übrigens wird der EAN-13-Code am häufigsten in Handels- und Einkaufszentren verwendet, sodass die Leute ihn häufiger sehen als andere Codetypen. Die Bitcodierung ist dieselbe wie in Code-128, die Datenstruktur finden Sie im Wikipedia-Artikel .

Fazit

Wie wir sehen können, kann selbst eine so einfache Sache wie ein Barcode einige coole Sachen enthalten. Übrigens ein weiterer kleiner Lifehack für Leser, die geduldig genug waren, um bis zu diesem Ort zu lesen - der Text unter dem Barcode ist vollständig identisch mit den Barcode-Daten. Es wurde für die Bediener erstellt, die den Code manuell eingeben können, wenn er vom Scanner nicht gelesen werden kann. So ist es einfach, den Barcode-Inhalt zu kennen - lesen Sie einfach den folgenden Text.

Danke fürs Lesen.