Julia und die Koordinatenabstiegsmethode

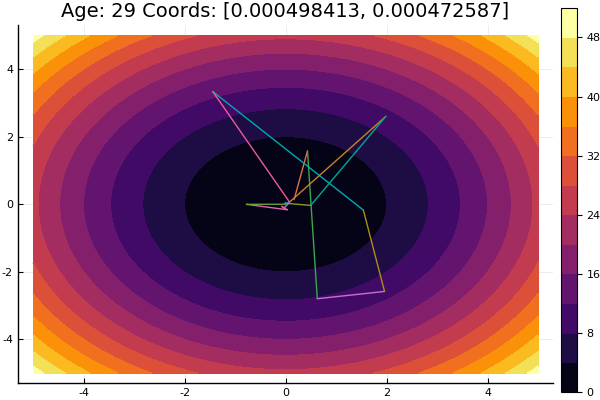
Die Methode des koordinatenweisen Abstiegs ist eine der einfachsten Methoden der mehrdimensionalen Optimierung und eignet sich gut, um ein lokales Minimum an Funktionen mit einer relativ glatten Topographie zu finden. Daher ist es besser, sich mit den Optimierungsmethoden vertraut zu machen.

Die Suche nach dem Extremum wird in Richtung der Koordinatenachsen durchgeführt, d.h. Während des Suchvorgangs wird nur eine Koordinate geändert. Somit reduziert sich ein mehrdimensionales Problem auf ein eindimensionales.

Algorithmus

Erster Zyklus:

• $$$x_1 = var$ , $$$x_2 = x_2 ^ 0$ , $$$x_3 = x_3 ^ 0$ , ..., $$$x_n = x_n ^ 0$ .
• Auf der Suche nach extremen Funktionen $$$f (x_1)$ . Setzen Sie das Extremum der Funktion auf den Punkt $$$x_1 ^ 1$ .
• $$$x_1 = x_1 ^ 1$ , $$$x_2 = var$ , $$$x_3 = x_3 ^ 0$ , ..., $$$x_n = x_n ^ 0$ . Extremum-Funktion $$$f (x_2)$ ist gleich $$$x_2 ^ 1$
• ...
• $$$x_1 = x_1 ^ 1$ , $$$x_2 = x_2 ^ 1$ , $$$x_3 = x_3 ^ 1$ , ..., $$$x_n = var$ .
  Als Ergebnis der Durchführung von n Schritten wurde ein neuer Ansatzpunkt für das Extremum gefunden $$$(x_1 ^ 1, x_2 ^ 1, ..., x_n ^ 1)$ . Als nächstes überprüfen wir das Kriterium für das Ende des Kontos: Wenn es erfüllt ist, wird die Lösung gefunden, andernfalls führen wir einen weiteren Zyklus durch.

Vorbereitung

Überprüfen Sie die Paketversionen:

(v1.1) pkg> status Status `C:\Users\User\.julia\environments\v1.1\Project.toml` [336ed68f] CSV v0.4.3 [a93c6f00] DataFrames v0.17.1 [7073ff75] IJulia v1.16.0 [47be7bcc] ORCA v0.2.1 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.3 [91a5bcdd] Plots v0.23.0 [ce6b1742] RDatasets v0.6.1 [90137ffa] StaticArrays v0.10.2 [8bb1440f] DelimitedFiles [10745b16] Statistics 

Wir definieren eine Funktion zum Zeichnen der Oberflächen- oder Ebenenlinien, in der es zweckmäßig wäre, die Grenzen des Diagramms anzupassen:

 using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end 

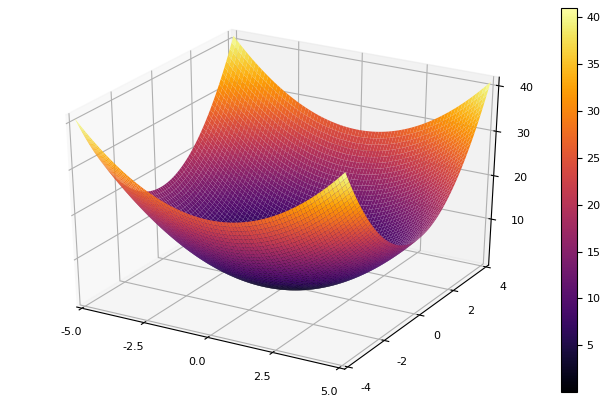
Als Modellfunktion wählen wir ein elliptisches Paraboloid

 parabol(x) = sum(u->u*u, x) fun = parabol plotter(surface, low = [-1 -1], up = [1 1]) 

Abstieg koordinieren

Wir implementieren die Methode in eine Funktion, die den Namen der eindimensionalen Optimierungsmethode, die Dimension des Problems, den gewünschten Fehler, die anfängliche Annäherung und die Einschränkungen für das Zeichnen von Linien auf Ebenen verwendet. Alle Parameter sind auf Standardwerte eingestellt.

 function ofDescent(odm; ndimes = 2, ε = 1e-4, fit = [.5 .5], low = [-1 -1], up = [1 1]) k = 1 #      sumx = 0 sumz = 1 plotter(contour, low = low, up = up) #    x = [ fit[1] ] #     y = [ fit[2] ] #      while abs(sumz - sumx) > ε && k<80 fitz = copy(fit) for i = 1:ndimes odm(i, fit, ε) #    end push!(x, fit[1]) push!(y, fit[2]) sumx = sum(abs, fit ) sumz = sum(abs, fitz) #println("$k $fit") k += 1 end #     scatter!(x', y', legend = false, marker=(10, 0.5, :orange) );# , ,  p = title!("Age = $(size(x,1)) f(x,y) = $(fun(fit))") end 

Als nächstes werden wir verschiedene Methoden der eindimensionalen Optimierung ausprobieren.

Newtons Methode

$$

$$x_ {n + 1} = x_n - \ frac {f (x_n)} {f '(x_n)}$$

Die Idee der Methode ist ebenso einfach wie die Implementierung

 #  dfun = (x, i) -> i == 1 ? 2x[1] + x[2]*x[2] : 2x[2] + x[1]*x[1] function newton2(i, fit, ϵ) k = 1 oldfit = Inf while ( abs(fit[i] - oldfit) > ϵ && k<50 ) oldfit = fit[i] tryfit = fun(fit) / dfun(fit, i) fit[i] -= tryfit println(" $k $fit") k+=1 end end ofDescent(newton2, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

Newton stellt hohe Anforderungen an die anfängliche Annäherung, und ohne Einschränkung der Stufen kann er problemlos auf unbekannte Entfernungen fahren. Die Berechnung der Ableitung ist wünschenswert, auf kleine Abweichungen kann jedoch verzichtet werden. Wir ändern unsere Funktion:

 function newton(i, fit, ϵ) k = 1 oldfit = Inf x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) while ( abs(oldfit - fit[i]) > ϵ && k<50 ) fx = fun(fit) oldfit = fit[i] fit[i] += 0.01 dfx = fun(fit) fit[i] -= 0.01 tryfit = fx*0.01 / (dfx-fx) #        if( abs(tryfit) > abs(fit[i])*10 ) push!(x, fit[1]) push!(y, fit[2]) break end fit[i] -= tryfit #println(" $k $fit") push!(x, fit[1]) push!(y, fit[2]) k+=1 end #  - -   plot!(x, y, w = 3, legend = false, marker = :rect ) end ofDescent(newton, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

Inverse parabolische Interpolation

Eine Methode, die keine Kenntnis der Ableitung erfordert und eine gute Konvergenz aufweist

 function ipi(i, fit, ϵ) # inverse parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.15 xn[i] = fit[i] + 0.15 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<80 fn = fun(xn) a = fn1*fn / ( (fn2-fn1)*(fn2-fn ) ) b = fn2*fn / ( (fn1-fn2)*(fn1-fn ) ) c = fn2*fn1 / ( (fn -fn2)*(fn -fn1) ) xnp[i] = a*xn2[i] + b*xn1[i] + c*xn[i] xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(ipi, fit = [0.1 0.1], low = [-.1 -.1], up = [.4 .4]) 

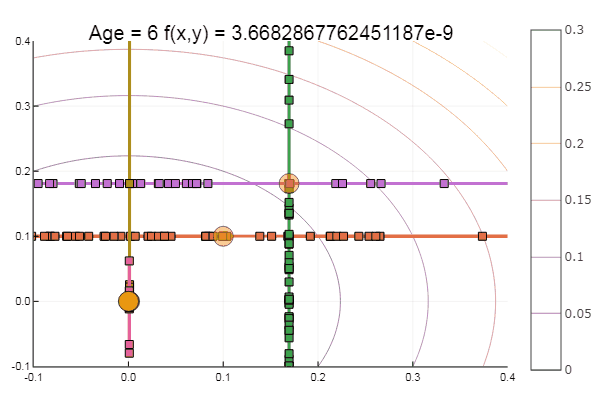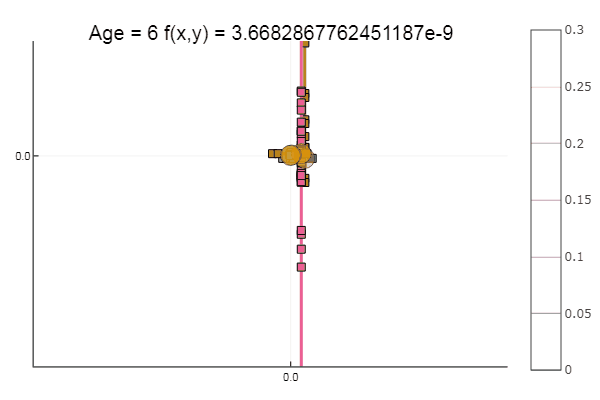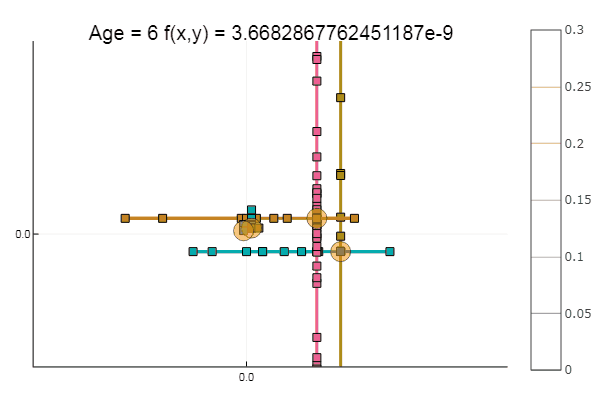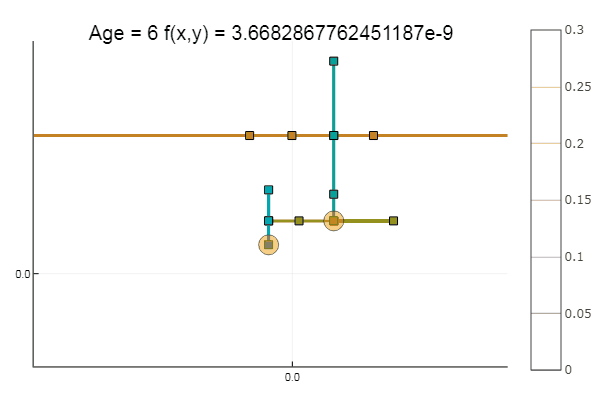
Wenn wir die anfängliche Annäherung verschlechtern, wird die Methode eine immense Anzahl von Schritten für jede Ära des Koordinatenabfalls erfordern. In dieser Hinsicht gewinnt sein Bruder

Sequentielle parabolische Interpolation

Es erfordert auch drei Startpunkte , zeigt jedoch bei vielen Testfunktionen zufriedenstellendere Ergebnisse.

 function spi(i, fit, ϵ) # sequential parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.01 xn[i] = fit[i] + 0.01 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<200 fn = fun(xn) v0 = xn1[i] - xn2[i] v1 = xn[i] - xn2[i] v2 = xn[i] - xn1[i] s0 = xn1[i]*xn1[i] - xn2[i]*xn2[i] s1 = xn[i] *xn[i] - xn2[i]*xn2[i] s2 = xn[i] *xn[i] - xn1[i]*xn1[i] xnp[i] = 0.5(fn2*s2 - fn1*s1 + fn*s0) / (fn2*v2 - fn1*v1 + fn*v0) xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(spi, fit = [16.1 16.1], low = [-.1 -.1], up = [.4 .4]) 

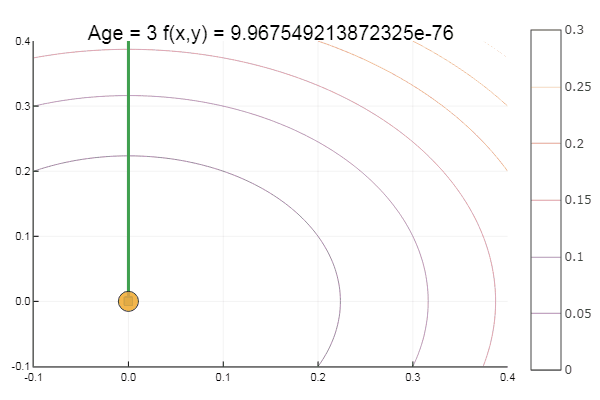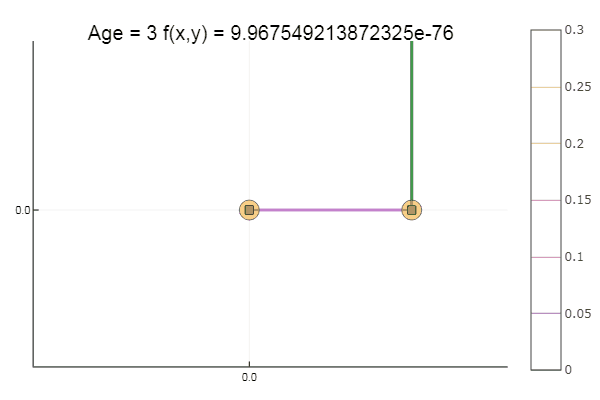
Das Verlassen eines sehr beschissenen Ausgangspunkts erfolgte in drei Schritten! Gut ... Aber alle Methoden haben einen Nachteil - sie konvergieren zu einem lokalen Minimum. Nehmen wir nun Ackleys Funktion für die Forschung

$$

$$f (x, y) = - 20 \ exp \ left [-0,2 {\ sqrt {0,5 \ left (x ^ {2} + y ^ {2} \ right)}} \ right] - \ exp \ left [ 0,5 \ links (\ cos 2 \ pi x + \ cos 2 \ pi y \ rechts) \ rechts] + e + 20$$

 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly plotter(surface, low = [-5 -5], up = [5 5]) 

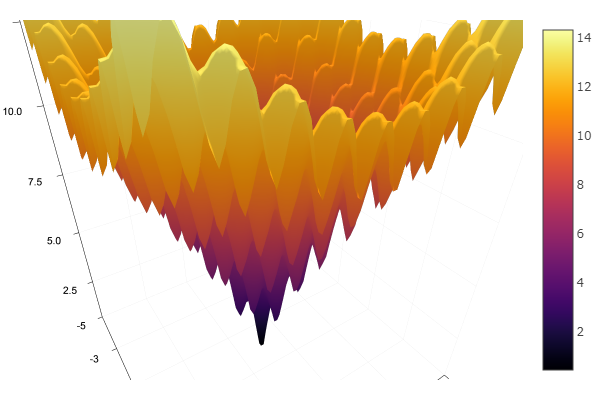
 ofDescent(spi, fit = [1.4 1.4], low = [-.1 -.1], up = [2.4 2.4]) 

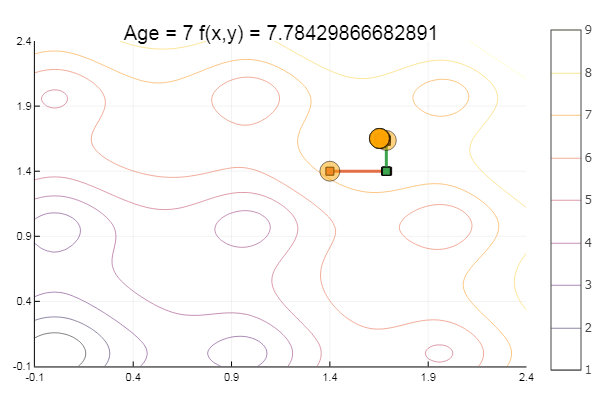
Goldener Schnitt-Methode

Theorie Obwohl die Implementierung kompliziert ist, zeigt sich die Methode manchmal gut, indem lokale Minima übersprungen werden

 function interval(i, fit, st) d = 0. ab = zeros(2) fitc = copy(fit) ab[1] = fitc[i] Fa = fun(fitc) fitc[i] -= st Fdx = fun(fitc) fitc[i] += st if Fdx < Fa st = -st end fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) while Fb < Fa d = ab[1] ab[1] = ab[2] Fa = Fb fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) # println("----", Fb, " ", Fa) end if st < 0 c = ab[2] ab[2] = d d = c end ab[1] = d ab end function goldsection(i, fit, ϵ) ϕ = Base.MathConstants.golden ab = interval(i, fit, 0.01) α = ϕ*ab[1] + (1-ϕ)*ab[2] β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = α Fa = fun(fit) fit[i] = β Fb = fun(fit) while abs(ab[2] - ab[1]) > ϕ if Fa < Fb ab[2] = β β = α Fb = Fa α = ϕ*ab[1] + (1-ϕ)*ab[2] fit[i] = α Fa = fun(fit) else ab[1] = α α = β Fa = Fb β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = β Fb = fun(fit) end println(">>>", i, ab) plot!(ab, w = 1, legend = false, marker = :rect ) end fit[i] = 0.5(ab[1] + ab[2]) end ofDescent(goldsection, fit = [1.4 1.4], low = [-.1 -.1], up = [1. 1.]) 

Das ist alles mit koordiniertem Abstieg. Die Algorithmen der vorgestellten Methoden sind recht einfach, sodass die Implementierung in Ihrer bevorzugten Sprache nicht schwierig ist. In Zukunft können Sie die integrierten Tools der Julia- Sprache in Betracht ziehen, aber jetzt möchten Sie sozusagen alles mit Ihren Händen fühlen, Methoden komplizierter und effizienter betrachten, dann können Sie zur globalen Optimierung übergehen und gleichzeitig mit der Implementierung in einer anderen Sprache vergleichen.

Literatur

1. Zaitsev V.V. Numerische Methoden für Physiker. Nichtlineare Gleichungen und Optimierung: ein Tutorial. - Samara, 2005 - 86er Jahre.
2. Ivanov A. V. Computermethoden zur Optimierung optischer Systeme. Studienführer. –SPb: SPbSU ITMO, 2010 - 114s.
3. Popova T. M. Methoden der mehrdimensionalen Optimierung: Richtlinien und Aufgaben für die Laborarbeit in der Disziplin "Methoden der Optimierung" für Studierende der Richtung "Angewandte Mathematik" / comp. T. M. Popova. - Chabarowsk: Verlag des Pazifiks. Zustand Universität, 2012 .-- 44 p.