Geekly articles weekly

Julia, Gradientenabstieg und Simplex-Methode


Wir machen uns weiterhin mit mehrdimensionalen Optimierungsmethoden vertraut.


Als nächstes werden die Implementierung der Methode des schnellsten Abstiegs mit Analyse der Ausführungsgeschwindigkeit sowie die Implementierung der Nelder-Mead-Methode mittels der Sprachen Julia und C ++ vorgeschlagen.


Gradientenabstiegsmethode


Die Suche nach dem Extremum erfolgt schrittweise in Richtung Gradient (max) oder Anti-Gradient (min). Bei jedem Schritt in Richtung des Gradienten (Anti-Gradient) wird die Bewegung ausgeführt, bis die Funktion zunimmt (abnimmt).


Für die Theorie folgen Sie den Links:



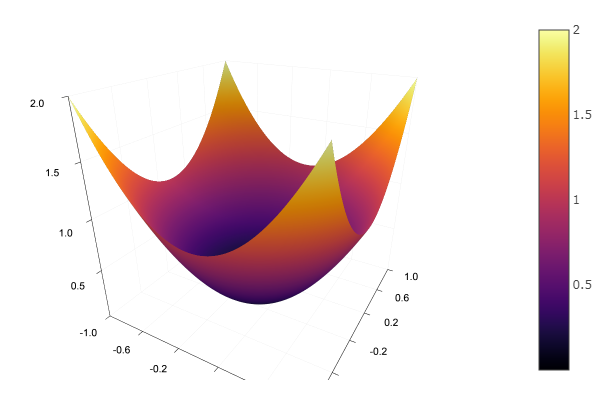
Mit der Modellfunktion wählen wir ein elliptisches Paraboloid und legen die Funktion zum Rendern des Reliefs fest:


using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end parabol(x) = sum(u->u*u, x) #   fun = parabol plotter(surface, low = [-1 -1], up = [1 1])


Wir definieren eine Funktion, die die Methode des steilsten Abstiegs implementiert, die die Dimension des Problems, die Genauigkeit, die Schrittlänge, die anfängliche Annäherung und die Größe des Begrenzungsrahmens berücksichtigt:


 # -- ,     -   function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) end #println(fun(fit)) end

Sie können sich auf die Funktion konzentrieren, die die Richtung des Gradienten im Hinblick auf die Optimierung berechnet.


Das erste, was mir in den Sinn kommt, sind Aktionen mit Matrizen:


 # \delta -      #      function grad(fit, δ) ndimes = length(fit) Δ = zeros(ndimes, ndimes) for i = 1:ndimes Δ[i,i] = δ end fr = [ fun( fit + Δ[:,i] ) for i=1:ndimes] fl = [ fun( fit - Δ[:,i] ) for i=1:ndimes] g = 0.5(fr - fl)/δ modg = sqrt( sum(x -> x*x, g) ) g /= modg end

Was wirklich gut ist, ist, dass Problembereiche leicht getestet werden können:


 #]add BenchmarkTools using BenchmarkTools @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 44.14 KiB allocs estimate: 738 -------------- minimum time: 76.973 μs (0.00% GC) median time: 81.315 μs (0.00% GC) mean time: 92.828 μs (9.14% GC) maximum time: 5.072 ms (94.37% GC) -------------- samples: 10000 evals/sample: 1

Sie können sich beeilen, alles im Sishny-Stil erneut einzugeben


 function grad(fit::Array{Float64,1}, δ::Float64) ndimes::Int8 = 2 g = zeros(ndimes) modg::Float64 = 0. Fr::Float64 = 0. Fl::Float64 = 0. for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= 2δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ modg += g[i]*g[i] end modg = sqrt( modg ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 14.06 KiB allocs estimate: 325 -------------- minimum time: 29.210 μs (0.00% GC) median time: 30.395 μs (0.00% GC) mean time: 33.603 μs (6.88% GC) maximum time: 4.287 ms (98.88% GC) -------------- samples: 10000 evals/sample: 1

Aber wie sich herausstellt, weiß es selbst und ohne uns, welche Typen eingestellt werden sollen, und so kommen wir zu einem Kompromiss:


 function grad(fit, δ) #    ndimes = length(fit) g = zeros(ndimes) for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= δ fit[i] -= δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ end modg = sqrt( sum(x -> x*x, g) ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 15.38 KiB allocs estimate: 409 -------------- minimum time: 28.026 μs (0.00% GC) median time: 30.394 μs (0.00% GC) mean time: 33.724 μs (6.29% GC) maximum time: 3.736 ms (98.72% GC) -------------- samples: 10000 evals/sample: 1

Nun lass ihn zeichnen:


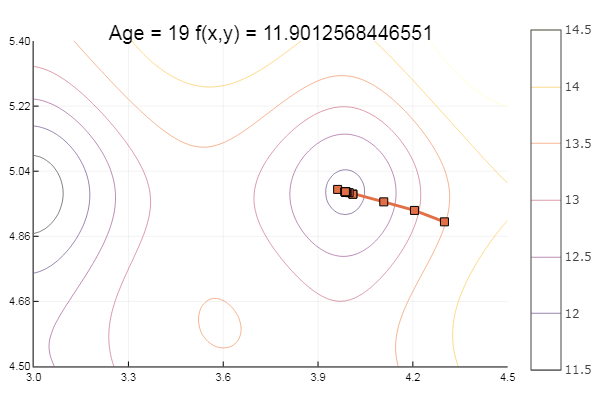
 function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) plotter(contour, low = low, up = up) while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) push!(x, fit[1]) push!(y, fit[2]) end plot!(x, y, w = 3, legend = false, marker = :rect ) title!("Age = $kf(x,y) = $(fun(fit))") println(fun(fit)) end ofGradient()


Probieren wir nun Ackleys Funktionen aus:


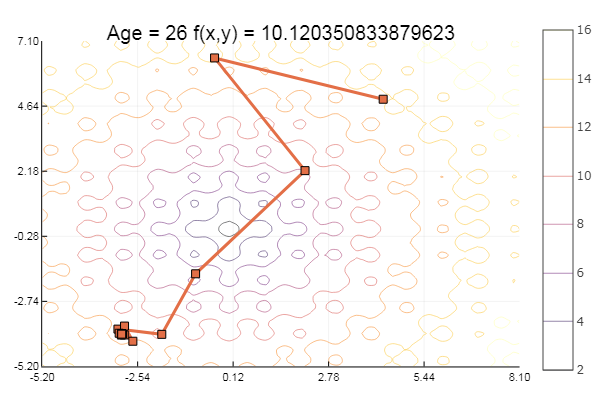
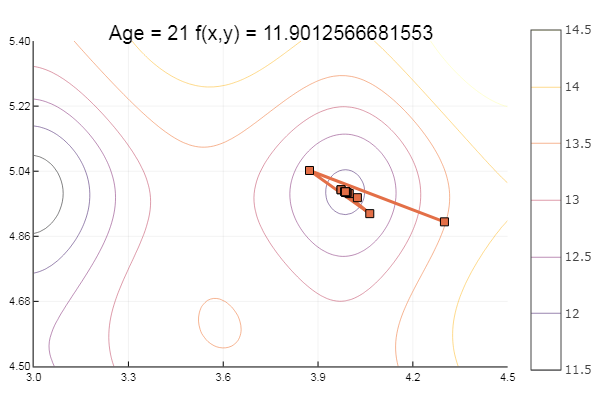
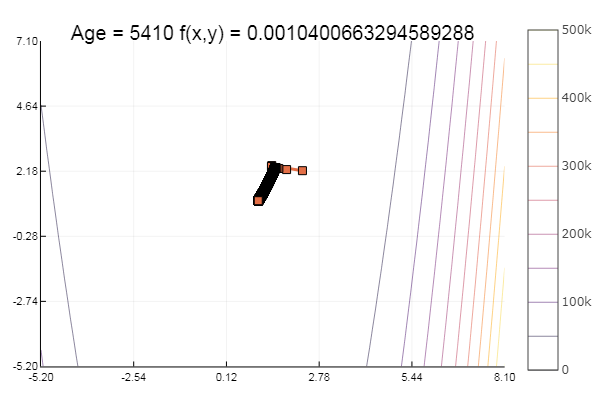
 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly ofGradient(fit = [4.3, 4.9], st = 0.1, low = [3 4.5], up = [4.5 5.4] )


Fiel in ein lokales Minimum. Machen wir weitere Schritte:


 ofGradient(fit = [4.3, 4.9], st = 0.9, low = [3 4.5], up = [4.5 5.4] ) 


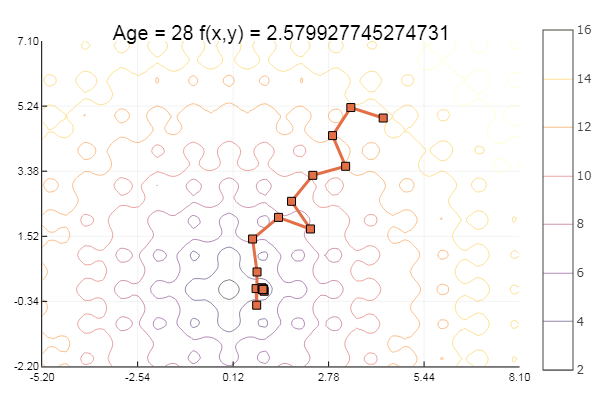
 ofGradient(fit = [4.3, 4.9], st = 1.9, low = [-5.2 -2.2], up = [8.1 7.1] )


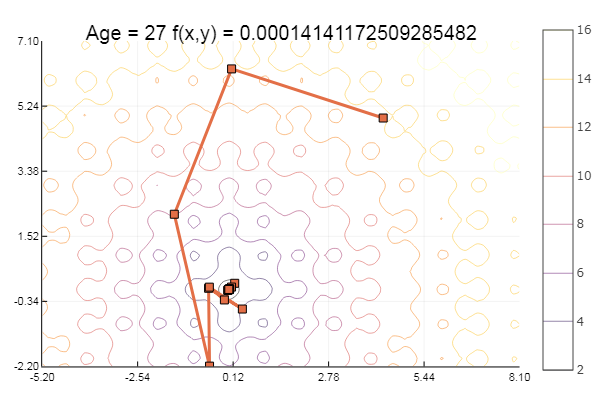
... und noch ein bisschen mehr:


 ofGradient(fit = [4.3, 4.9], st = 8.9, low = [-5.2 -2.2], up = [8.1 7.1] )


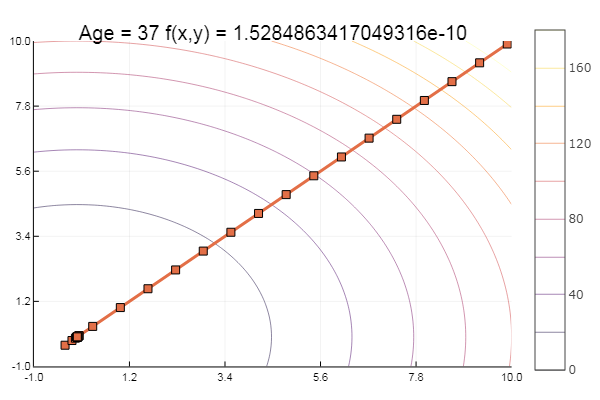
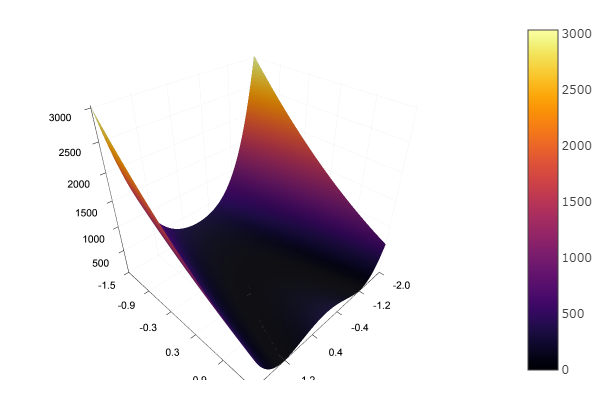
Großartig! Und jetzt etwas mit einer Schlucht, wie die Rosenbrock-Funktion:


 rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] fun = rosenbrok plotter(surface, low = [-2 -1.5], up = [2 1.5]) 


 ofGradient(fit = [2.3, 2.2], st = 9.9, low = [-5.2 -5.2], up = [8.1 7.1] ) 


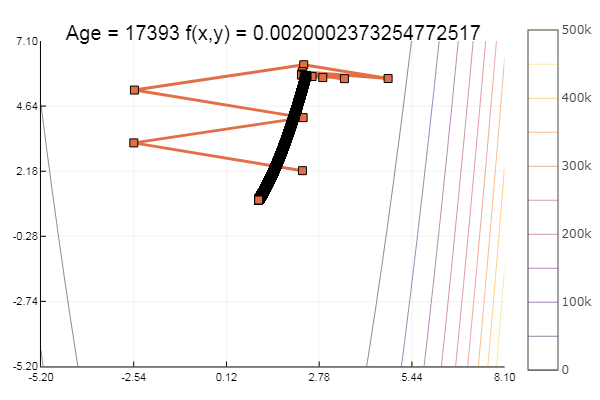
 ofGradient(fit = [2.3, 2.2], st = 0.9, low = [-5.2 -5.2], up = [8.1 7.1] )


Moral: Farbverläufe mögen keine Überdachungen.


Simplex-Methode


Die Nelder-Mead-Methode, auch als verformbare Polyeder-Methode und Simplex-Methode bekannt, ist eine Methode zur bedingungslosen Optimierung einer Funktion mehrerer Variablen, bei der die Ableitung (genauer gesagt Gradienten) der Funktion nicht verwendet wird, und ist daher leicht auf nicht glatte und / oder verrauschte Funktionen anwendbar.


Das Wesentliche der Methode ist die sequentielle Bewegung und Verformung eines Simplex um einen Extrempunkt.


Die Methode findet ein lokales Extremum und kann in einem von ihnen stecken bleiben. Wenn Sie immer noch ein globales Extremum finden müssen, können Sie versuchen, einen anderen anfänglichen Simplex zu wählen.


Hilfsfunktionen:


 #          function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] #     Mx[:, sortperm(f)] #Return a permutation vector I that puts v[I] in sorted order. end #   function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) vecl(x) = sqrt( sum(u -> u*u, x) )#   for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) #     end D sqrt(maximum(D)) end function simplexplot(xy, low, up) for i = 1:length(xy) if i%11 == 0 low *= 0.05 up *= 0.05 end Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] contour(Xs, Ys, Zs) xaxis!( low[1]:(up[1]-low[1])*0.2:up[1] ) yaxis!( low[2]:(up[2]-low[2])*0.2:up[2] ) plot!(xy[i][1,:], xy[i][2,:], w = 3, legend = false, marker = :circle ) title!("Age = $if(x,y) = $(fun(xy[i][:,1]))") savefig("$fun $i.png") end end

Und die Simplex-Methode selbst:


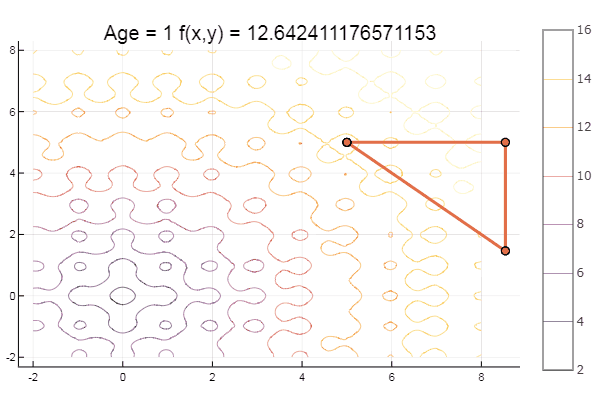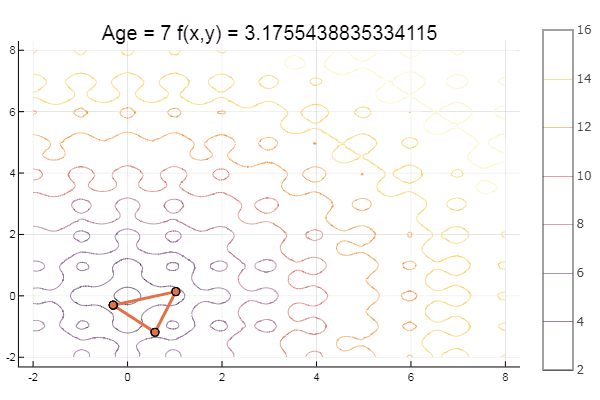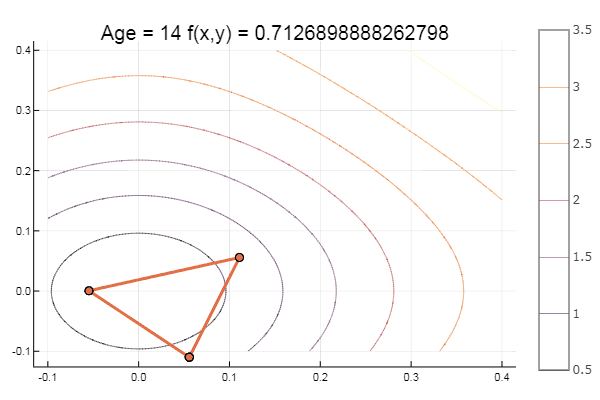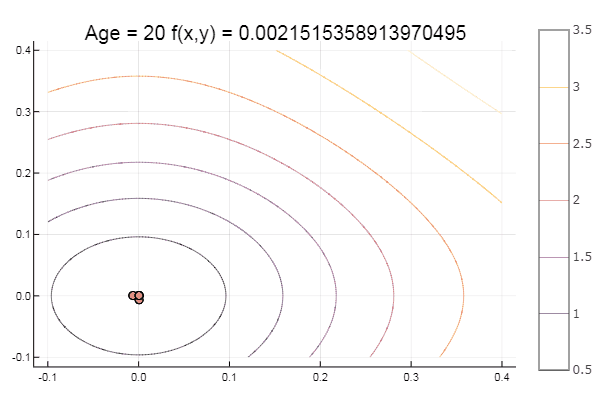
 function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) vecl(v) = sqrt( sum(x -> x*x, v) ) k = 0 N = ndimes Xx = zeros(N, N+1) coords = [] for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] #  - i-  Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end #println(k, " ", p, " ", Xx[:,1]) push!(coords, [Xx[:,1:3] Xx[:,1] ]) p = normx(Xx) end #while #simplexplot(coords, low, up) fit = Xx[:,1] end ofNelderMid(fit = [-9, -2], low = [-2 2], up = [-8 8])


Und zum Nachtisch etwas Buche ... zum Beispiel die Funktion von Bukin
f(x,y)=100 sqrt|y−0,01x2|+0,01|x+10|


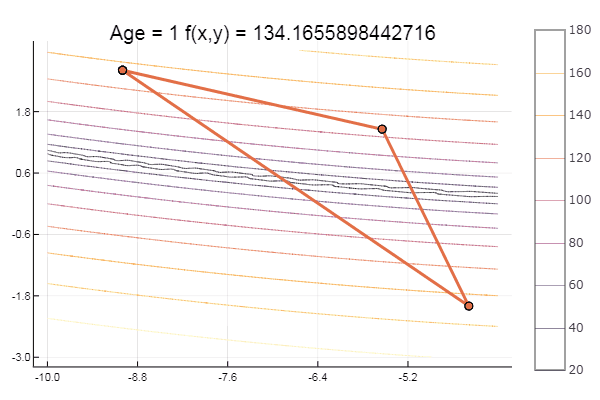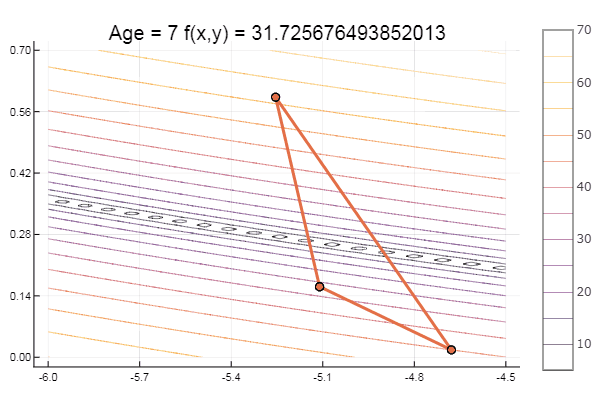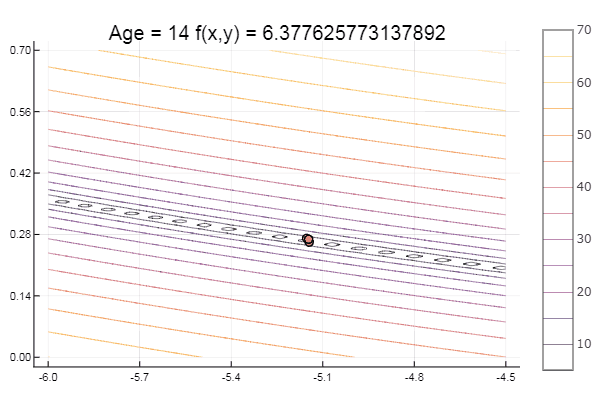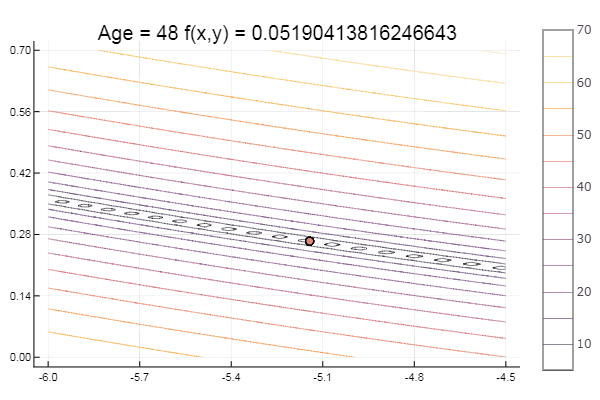
 bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] fun = bukin6 ofNelderMid(fit = [-10, -2], low = [-3 -7], up = [-8 -4.5])


Lokales Minimum - na ja, nichts, die Hauptsache ist, den richtigen Start-Simplex zu wählen, also habe ich für mich selbst einen Favoriten gefunden.


Bonus Methoden von Nelder-Mead, dem schnellsten Abstieg und Koordinatenabstieg in C ++


Alarm! 550 Codezeilen!
 /* * File: main.cpp * Author: User * * Created on 3  2017 ., 21:22 */ #include <iostream> #include <math.h> using namespace std; typedef double D; class Model { public: D *fit; D ps; Model(); DI(); }; Model :: Model() { ps = 1; fit = new D[3]; fit[0]=1.3; fit[1]=1.; fit[2]=2.; } D Model :: I() // rosenbrock { return 100*(fit[1]-fit[0]*fit[0]) * (fit[1]-fit[0]*fit[0]) + (1-fit[0])*(1-fit[0]); } class Methods : public Model { public: void ofDescent(); void Newton(int i); void SPI(int i); //sequential parabolic interpolation void Cutters(int i); void Interval(D *ab, D st, int i); void Gold_section(int i); void ofGradient(); void Grad(int N, D *g, D delta); void Srt(D **X, int N); void ofNelder_Mid(); D Nor(D **X, int N); }; void Methods :: ofDescent()//   { int i, j=0; D *z = new D[3]; D sumx, sumz; sumx = sumz = 0; do { sumx = sumz = 0; for(i=0; i<3; i++) z[i] = fit[i]; for(i=0; i<2; i++) { //Cutters(i); //SPI(i); Newton(i); //Gold_section(i); sumx += fit[i]; sumz += z[i]; } j++; //if(j%1000==0) cout << j << " " << fit[0] << " " << fit[1] << " " << fit[2] << " " << fit[3] << endl; //cout << sumz << " " << sumx << endl; } while(fabs(sumz - sumx) > 1e-6); delete[]z; } void Methods :: SPI(int i) { int k = 2; D f0, f1, f2; D v0, v1, v2; D s0, s1, s2; D *X = new D[300]; X[0] = fit[i] + 0.01; X[1] = fit[i]; X[2] = fit[i] - 0.01; while(fabs(X[k] - X[k-1]) > 1e-3) { fit[i] = X[k]; f0 = I(); fit[i] = X[k-1]; f1 = I(); fit[i] = X[k-2]; f2 = I(); v0 = X[k-1] - X[k-2]; v1 = X[k ] - X[k-2]; v2 = X[k ] - X[k-1]; s0 = X[k-1]*X[k-1] - X[k-2]*X[k-2]; s1 = X[k ]*X[k ] - X[k-2]*X[k-2]; s2 = X[k ]*X[k ] - X[k-1]*X[k-1]; X[k+1] = 0.5*(f2*s2 - f1*s1 + f0*s0) / (f2*v2 - f1*v1 + f0*v0); k++; cout << k << " " << X[k] << endl; } fit[i] = X[k]; delete[]X; } void Methods :: Newton(int i) { D dt, T, It; int k=0; while(fabs(T-fit[i]) > 1e-3) { It = I(); T = fit[i]; fit[i] += 0.01; dt = I(); fit[i] -= 0.01; fit[i] -= It*0.001 / (dt - It); cout << k << " " << fit[i] << endl; k++; } } void Methods :: Cutters(int i) { D Tn, Tnm, Tnp, It, Itm; int j=0; Tn = 0.15; Tnm = 2.65;//otrezok Itm = I(); //cout << Tnm << " " << Tn << endl; while(fabs(Tn-Tnm) > 1e-6) { fit[i] = Tn; It = I(); Tnp = Tn - It * (Tn-Tnm) / (It-Itm); cout << j+1 << " " << Tnp << endl; Itm = It; Tnm = Tn; Tn = Tnp; j++; } fit[i] = Tnp; } void Methods :: Interval(D *ab, D st, int i) { D Fa, Fdx, d, c, Fb, fitbox = fit[i]; ab[0] = fit[i]; Fa = I(); fit[i] -= st; Fdx = I(); fit[i] += st; if(Fdx < Fa) st = -st; fit[i] += st; ab[1] = fit[i]; Fb = I(); while(Fb < Fa) { d = ab[0]; ab[0] = ab[1]; Fa = Fb; fit[i] += st; ab[1] = fit[i]; Fb = I(); cout << Fb << " " << Fa << endl; } if(st<0) { c = ab[1]; ab[1] = d; d = c; } ab[0] = d; fit[i] = fitbox; } void Methods :: Gold_section(int i) { D Fa, Fb, al, be; D *ab = new D[2]; D st = 0.5; D e = 0.5*(sqrt(5) - 1); Interval(ab, st, i); al = e*ab[0] + (1-e)*ab[1]; be = e*ab[1] + (1-e)*ab[0]; fit[i] = al; Fa = I(); fit[i] = be; Fb = I(); while(fabs(ab[1]-ab[0]) > e) { if(Fa < Fb) { ab[1] = be; be = al; Fb = Fa; al = e*ab[0] + (1-e)*ab[1]; fit[i] = al; Fa = I(); } if(Fa > Fb) { ab[0] = al; al = be; Fa = Fb; be = e*ab[1] + (1-e)*ab[0]; fit[i] = be; Fb = I(); } cout << ab[0] << " " << ab[1] << endl; } fit[i] = 0.5*(ab[0] + ab[1]); cout << ab[0] << " " << ab[1] << endl; } void Methods :: Grad(int N, D *g, D delta)//   { int n; D Fr, Fl, modG=0; for(n=0; n<N; n++) { fit[n] += delta; Fr = I(); fit[n] -= delta; fit[n] -= delta; Fl = I(); fit[n] += delta; g[n] = (Fr - Fl)*0.5/delta; modG += g[n]*g[n]; } modG = sqrt(modG); for(n=0; n<N; n++) g[n] /= modG; g[N] = I(); } void Methods :: ofGradient() { int n, j=0; D Fun, st, eps; const int N = 2; D *g = new D[N+1]; st = 0.1; eps = 0.000001; while(st > eps) { Grad(N,g,0.0001); for(n=0; n<N; n++) fit[n] -= st*g[n]; Fun = I(); if(Fun >= g[N]) { st /= 2.; for(n=0; n<N; n++) fit[n] += st*g[n]; } j++; cout << j << " " << fit[0]/ps << " " << fit[1]/ps << " " << fit[2]/ps<< endl; } } void Methods :: ofNelder_Mid() { int i, j, k; D modz = 0., p, eps = 1e-3; D FR, FN, F0, FE, FNm1, FC; const int N = 2; D *Co = new D[N]; D *Eo = new D[N]; D *Ro = new D[N]; D *Xo = new D[N]; D **Xx = new D*[N]; D **dz = new D*[N]; for(i=0;i<N;i++) { dz[i] = new D[N]; Xx[i] = new D[N+1]; } for(i=0;i<N;i++) for(j=0;j<N;j++) if(i^j) dz[i][j] = 0; else dz[i][j] = 1; for(i=0;i<N;i++) Xx[i][N] = fit[i]; for(i=0;i<N;i++) modz += fit[i]*fit[i]; modz = sqrt(modz); for(i=0;i<N;i++) dz[i][i] = 0.5*modz; for(i=0;i<N;i++) for(j=0;j<N;j++) Xx[i][j] = fit[i] + dz[i][j]; k = 0; p = Nor(Xx, N); while(p > eps) { k++; Srt(Xx, N); for(i=0;i<N;i++) Xo[i] = 0.; for(i=0;i<N;i++) for(j=0;j<N;j++) Xo[i] += Xx[i][j]; for(i=0;i<N;i++) Xo[i] /= N; for(i=0;i<N;i++) Ro[i] = Xo[i] + (Xo[i]-Xx[i][N]); for(i=0;i<N;i++) fit[i] = Ro[i]; FR = I(); for(i=0;i<N;i++) fit[i] = Xx[i][N]; FN = I(); if(FR > FN) { for(i=0;i<N;i++) for(j=1;j<=N;j++) Xx[i][j] = 0.5*(Xx[i][0] + Xx[i][j]); } else { for(i=0;i<N;i++) fit[i] = Xx[i][0]; F0 = I(); if(FR < F0) { for(i=0;i<N;i++) Eo[i] = Xo[i] +2*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Eo[i]; FE = I(); if(FE < FR) for(i=0;i<N;i++) Xx[i][N] = Eo[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } else { for(i=0;i<N;i++) fit[i] = Xx[i][N-1]; FNm1 = I(); if(FR <= FNm1) for(i=0;i<N;i++) Xx[i][N] = Ro[i]; else { for(i=0;i<N;i++) Co[i] = Xo[i] +0.5*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Co[i]; FC = I(); if(FC < FR) for(i=0;i<N;i++) Xx[i][N] = Co[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } } } for(i=0;i<N;i++) cout << Xx[i][0] << " "; cout << k << " " << p << endl; p = Nor(Xx, N); if(p < eps) break; } for(i=0;i<N;i++) fit[i] = Xx[i][0]; /*for(i=0;i<N;i++) { for(j=0;j<N+1;j++) cout << Xx[i][j] << " "; cout << endl; }*/ delete[]Co; delete[]Xo; delete[]Ro; delete[]Eo; for(i=0;i<N;i++) { delete[]dz[i]; delete[]Xx[i]; } } //   D Methods :: Nor(D **X, int N) { int i, j, k; D norm, xij, pn = 0.; for(i=0;i<N;i++) for(j=i+1;j<=N;j++) { xij = 0.; for(k=0;k<N;k++) xij += ( (X[k][i]-X[k][j])*(X[k][i]-X[k][j]) ); pn = sqrt(xij);//    if(norm > pn) norm = pn;//   } return sqrt(norm); } //    void Methods :: Srt(D **X, int N) { int i, j, k; D temp; D *f = new D[N+1]; D *box = new D[N]; D **y = new D*[N+1]; for(i=0;i<N+1;i++)//  y[i] = new D[N+1]; for(i=0;i<N;i++) box[i] = fit[i];//    for(i=0;i<=N;i++) { for(j=0;j<N;j++) fit[j] = X[j][i]; f[i] = I();//     } for(i=0;i<N;i++) fit[i] = box[i];//    for(i=0;i<N;i++) for(j=0;j<=N;j++) y[i][j] = X[i][j]; for(i=0;i<=N;i++) y[N][i] = f[i];//stack(X, f) //    , //     N    for(i=1;i<=N;i++) for(j=0;j<=Ni;j++) if(y[N][j] >= y[N][j+1]) for(k=0;k<=N;k++) { temp = y[k][j]; y[k][j] = y[k][j+1]; y[k][j+1] = temp; } //submatrix   for(i=0;i<N;i++) for(j=0;j<=N;j++) X[i][j] = y[i][j]; /* for(i=0;i<=N;i++) { for(j=0;j<=N;j++) cout << y[i][j] << " "; cout << endl; } */ for(i=0;i<N+1;i++) delete[]y[i]; delete[]box; delete[]f; } int main() { Methods method; //method.ofDescent(); //method.ofGradient(); method.ofNelder_Mid(); return 0; }

Genug für heute. Der nächste Schritt ist logisch, etwas aus der globalen Optimierung auszuprobieren, weitere Testfunktionen einzugeben und dann Pakete mit integrierten Methoden zu studieren.

Source: https://habr.com/ru/post/de440070/

More articles:


All Articles