👚 🤳 ㊙️ Wie funktionieren technische Indikatoren an der Börse tatsächlich? 🧚 🤲🏽 💜

Jeder, der sich jemals für Aktien oder Kryptowährungen interessiert hat, hat diese zusätzlichen Linien in den Diagrammen gesehen. Sie haben vielleicht die Meinung gehört, dass sie nicht funktionieren. Aber sie verbessern meine Handelsfähigkeit erheblich, während sie viele wichtige Daten anzeigen. Aber wie funktionieren sie eigentlich? Und für wen kann es nützlich sein?

Sie sollten dies unbedingt lesen, wenn:

Sie verwenden sie im Tageshandel
Sie planen, einen Handelsbot zu schreiben
Wenn Sie eine Handelsstrategie oder Indikatoren selbst implementieren möchten

Am häufigsten sind technische Indikatoren eine Fensterfunktion, eine rekursive Funktion oder eine gewichtete Funktion von Preisen / Volumina, die im UOHLCV-Format (Unix-Zeit, offen, hoch, niedrig, geschlossen, Volumen) von der Börse gezogen werden. Es ist nicht ungewöhnlich, dass Indikatoren unterschiedliche Filter, Minima und Maxima oder andere Indikatoren als Grundlage für nachfolgende Berechnungen verwenden.

Einfacher gleitender Durchschnitt (SMA)

Bei der Codierung von Indikatoren ist es sehr praktisch, einen funktionalen Ansatz zu verwenden. Beispielsweise ist der gleitende Durchschnitt nur der Durchschnitt jedes Werts des rollenden Fensters.

function sma($close, window) { return rolling(x => mean(x), window, $close); }

Dabei ist der Mittelwert die Operation, die den Durchschnitt von Array berechnet, und das Rollen die Kombination der Fensterfunktion, die für jedes vorhandene Element im Array ein Array der letzten n Elemente erzeugt, und der Operation , die dieses Fenster zu einer Zahl faltet.

 function rolling(operation, window, array) { let result = []; for (let i = 0; i < array.length; i++) { if (i + 1 < window) { result.push(NaN); } else { result.push(operation(array.slice(i + 1 - window, i + 1))); } } return result; }

Der SMA ist ein nachlaufender Indikator und hilft bei der Bestimmung des Trends. Es wird als Überlagerung im Diagramm gezeichnet und die ersten Werte werden normalerweise verworfen. Zwei gleitende Durchschnitte können zusammen verwendet werden, um Überkreuzungssignale zu erzeugen.

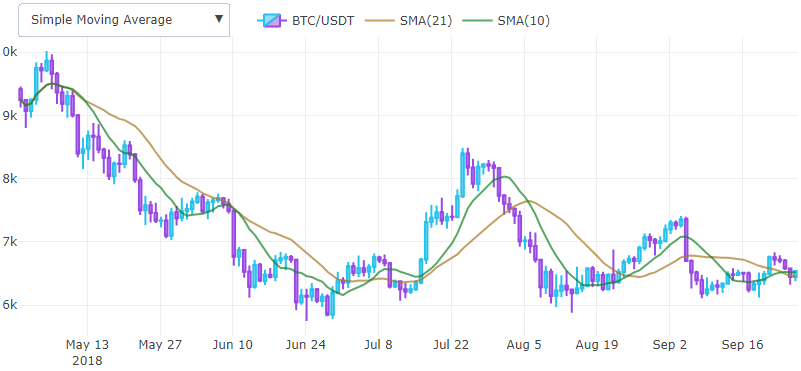
Einfacher gleitender Durchschnitt (SMA)

Ein bullischer Crossover tritt auf, wenn ein relativ kurzer gleitender Durchschnitt einen langen gleitenden Durchschnitt ausbricht. Exponentiell gewichteter gleitender Durchschnitt wird in der Praxis häufiger verwendet, da eine gewichtete Fensterfunktion den Verzögerungseffekt verringert.

Standardabweichung (STDEV)

Wenn wir die mittlere Funktion in SMA durch die Standardabweichung ersetzen , erhalten wir eine gleitende Standardabweichung

 function stdev($close, window) { return rolling(x => sd(x), window, $close); }

Wobei sd als Quadratwurzel der Varianz betrachtet wird und üblicherweise ohne Bessel-Korrektur. Wir gehen davon aus, dass jeder versteht, wie man SD implementiert

s d (x) = s q r t f r a c s u m (x_{i} - h a t x)^{2} N .

$sd (x) = \ sqrt {\ frac {\ sum (x_i- \ hat x) ^ 2} {N}}.$

Die Quadratwurzel der Varianz wird verwendet, weil die Varianz selbst in Bezug auf die Dimensionstheorie in US-Dollar gemessen wird und nicht, weil jemand eine Marke oder was auch immer eingetragen hat.

Bollinger Bands (BBAND)

Daher haben wir bereits zwei grundlegende Indikatoren implementiert, die wir kombinieren und neue erhalten können. Wenn wir zum Beispiel die punktweise Addition des gleitenden Durchschnitts und der Standardabweichung multipliziert mit 2 betrachten, erhalten wir den oberen Teil des Bollinger-Bandes und den unteren Teil, wenn wir subtrahieren.

 function bb($close, window, mult) { let middle = sma($close, window); let upper = pointwise((a, b) => a + b * mult, middle, stdev($close, window)); let lower = pointwise((a, b) => a - b * mult, middle, stdev($close, window)); return { lower : lower, upper : upper}; }

wobei die Funktion punktweise eine weitere nützliche Funktion ist

 export function pointwise(operation, ...arrays) { let result = []; for (let i = 0, len = arrays[0].length; i < len; i++) { let iarr = (i) => arrays.map(x => x[i]); result[i] = operation(...iarr(i)); } return result; }

und es wird nur eine Operation mit mehreren Arrays ausgeführt

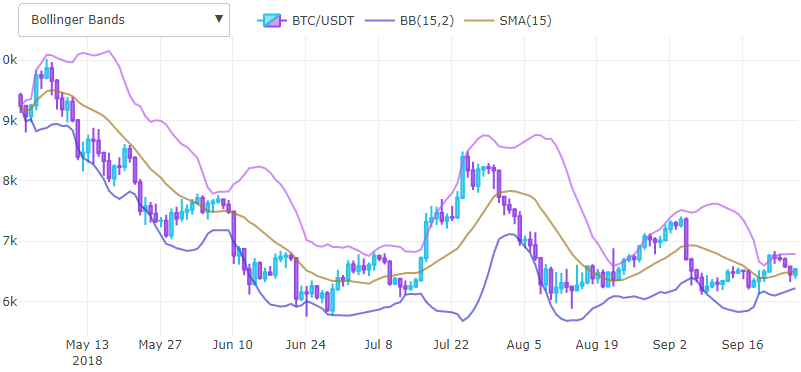
Bollinger Bands (BBAND)

Bollinger-Bänder helfen dabei, die Ruhe vor der großen Preisbewegung zu bestimmen, und werden als Instrument verwendet, um die Volatilität direkt auf dem Chart zu verschieben. Die Standardabweichung wird vom gleitenden Durchschnitt abgezogen / addiert, um als Überlagerung auf einem Chart mit dem Preis angezeigt zu werden.

Exponentieller gleitender Durchschnitt (EMA)

Wie können wir die Verzögerung des einfachen gleitenden Durchschnitts verringern? Da es den Mittelwert der letzten n Schlusskurse berechnet, können wir verstehen, dass wir eine Summierung mit etwas Gewicht durchführen und den Beitrag der alten Preise reduzieren können.

b a r x = f r a c s u m x_{i} N = f r a c s u m 1 c d o t x_{i} s u m 1 q u a d R i g h t a r r o w q u a d w i d e t i l d e x = f r a c s u m x_{i} w_{i} s u m w_{i}

$\ bar x = \ frac {\ sum x_i} {N} = \ frac {\ sum 1 \ cdot x_i} {\ sum 1} \ quad \ Rightarrow \ quad \ widetilde {x} = \ frac {\ sum x_i w_i } {\ sum w_i}$

Zum Beispiel, wenn wir wählen

w_{n} = q^{n}

$w_n = q ^ n$ und eine Konstante

q

$q$ das ist weniger als eins, dann bekommen wir ein unendlich abnehmendes Gewicht, wenn wir die Preise beginnend mit dem neuesten addieren.

gewichtete Funktionen

Es ist auch möglich, Berechnungen zu approximieren und eine rekursive Gleichung zu erhalten, wenn wir das Fenster auf die volle Länge erweitern und annehmen, dass der Beitrag der Schwänze gering ist.

1 + q + q^{2} + . . . + q^{n} u n d e r s e t n t o i n f t y u n d e r s e t q < 0 = f r a c 1 1 - q m a t h r m {E M A}_{c u r r} = f r a c s u m x_{i} q^{i} s u m q^{i} = (1 - q) s u m x_{i} q^{i} m a t h r m {E M A}_{n e x t} = f r a c x_{n e x t} + q c d o t s u m x_{i} q^{i} 1 + q c d o t s u m q^{i} = (1 - q) c d o t l e f t [x_{n e x t} + q c d o t S u m m e x_{i} q^{i} r i g h t] m a t h r m {E M A}_{n e x t} = (1 - q) c d o t x_{n e x t} + q) c d o t m a t h r m {E M A}_{c u r r}

$1 + q + q ^ 2 + ... + q ^ n \ underset {n \ to \ infty} {\ underset {q <0} {=}} \ frac {1} {1-q} \\ \ mathrm {EMA} _ {curr} = \ frac {\ sum x_i q ^ i} {\ sum q ^ i} = (1-q) \ sum x_i q ^ i \\ \ mathrm {EMA} _ {next} = \ frac {x_ {next} + q \ cdot \ sum x_i q ^ i} {1 + q \ cdot \ sum q ^ i} = (1-q) \ cdot \ left [x_ {next} + q \ cdot \ Summe x_i q ^ i \ right] \\ \ mathrm {EMA} _ {next} = (1-q) \ cdot x_ {next} + q) \ cdot \ mathrm {EMA} _ {curr}$

Finnisch brauchen wir einen Wert α = 1 - q als Glättungskonstante. Es ist möglich, dies zu beweisen , wenn wir uns entscheiden

a l p h a = 2 / (N + 1)

$\ alpha = 2 / (N + 1)$ Der Schwerpunkt der obigen EMA- und SMA-Gewichtstabellen wird gleich. Im Code sieht dies viel einfacher aus.

 function ema($close, window, weight = null) { weight = weight ? weight : 2 / (window + 1); let ema = [ mean($close.slice(0, window)) ]; for (let i = 1; i < $close.length; i++) { ema.push($close[i] * weight + ema[i - 1] * (1 - weight)); }; return ema; }

Im Allgemeinen ist dies der gleiche gleitende Durchschnitt, jedoch empfindlicher.

Exponentieller gleitender Durchschnitt (EMA)

Die Effektivität der Nutzung hängt von Ihrer Erfahrung und den verwendeten Einstellungen ab. Zum Beispiel auf dieser Seite sind die Parameter ziemlich gut gewählt.

Moving Average Convergence Divergence (MACD)

Gerald Appel entwickelte 1979 einen der einfachsten und effektivsten verfügbaren Indikatoren. Es verwandelt zwei Trend-EMA-Indikatoren in einen Momentum-Oszillator und bietet das Beste aus beiden Welten: Trendfolge und Momentum. Grob gesagt ist das MACD-Histogramm eine Ableitung des Preises. Es wird in einem neuen Koordinatensystem anstatt in einer Überlagerung gezeichnet und mit zwei Linien und einem Histogramm dargestellt.

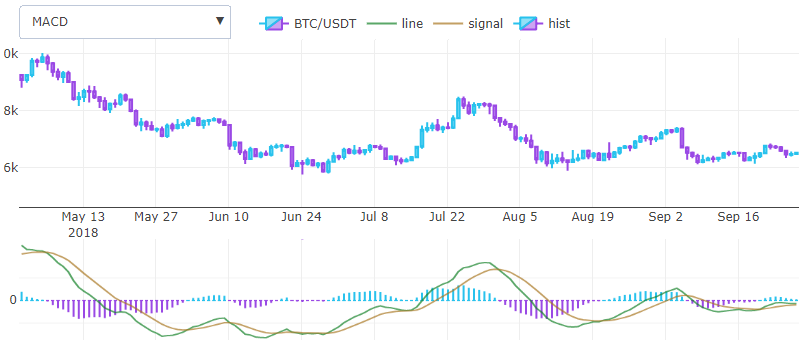
Moving Average Convergence Divergence (MACD)

Um die MACD-Linie zu berechnen, müssen wir lange EMA von kurzen subtrahieren, das ist alles. Eine andere EMA dieser Leitung mit winzigem Fenster erzeugt die Signalleitung. Das Histogramm wird durch Differenz zwischen den beiden vorherigen Ergebnissen erhalten.

 function macd($close, wshort, wlong, wsig) { let line = pointwise((a, b) => a - b, ema($close, wshort), ema($close, wlong)); let signal = ema(line, wsig); let hist = pointwise((a, b) => a - b, line, signal); return { line : line, signal : signal, hist : hist }; }

Korrelationsmatrix

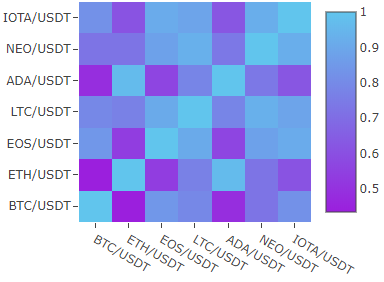
Wenn Sie sich für langfristige Investitionen und Portfolioanalysen interessieren, finden Sie die Korrelationsmatrix nützlich.

 function cor(f, g) { let Ef = mean(f), Eg = mean(g); let Ef2 = mean(pointwise((a) => a * a, f)); let Eg2 = mean(pointwise((a) => a * a, g)); let Efg = mean(pointwise((a, b) => a * b, f, g)); return (Efg - Ef * Eg) / Math.sqrt((Ef2 - Ef * Ef) * (Eg2 - Eg * Eg)); }

Hier Korrelationsmatrix verschiedener Kryptoassets in 2 Monaten.

Prüfung der Anzeigeeinheit

Wenn wir genaue Tabellen mit Indikatorwerten haben, können wir unsere Berechnung genau testen. Es gibt verschiedene Möglichkeiten, das Fehlermaß zwischen den beiden Funktionen zu bestimmen. In diesem Fall passt der normalisierte mittlere quadratische Fehler jedoch besser, da er im Gegensatz zu RMSE dimensionslos und relativ ist.

m a t h r m N R M S E = l e f t . s q r t f r a c s u m (h a t x_{i} - x_{i})^{2} N m i d d l e / (m a x x_{i} - m i n x_{i}) r i g h t .

$\ mathrm {NRMSE} = \ left. \ sqrt {\ frac {\ sum (\ hat x_i - x_i) ^ 2} {N}} \ middle / (\ max {x_i} - \ min {x_i}) \ right.$

Zum Beispiel kann Bitcoin 20.000 USD kosten und ein Unterschied von 10 USD ist gering, während der gesamte Altcoin 1 USD kosten kann und der Unterschied von 10 USD sehr groß ist.

 function nrmse(f, g) { let sqrDiff = pointwise((a, b) => (a - b) * (a - b), f, g); return Math.sqrt(mean(sqrDiff)) / (Math.max(...f) - Math.min(...f)); }

Wir können auch MAPE verwenden, aber es ist nicht kommutativ und hat ein Problem nahe Null.

Fazit

Das war's also. In ein paar Zeilen Code können wir die grundlegenden technischen Indikatoren ausdrücken. Wenn Ihnen diese Erklärung gefällt, überprüfen Sie meine Bibliothek auf Github. Dort finden Sie noch viel mehr. Wenn Sie einige Algorithmen für maschinelles Lernen für Ihren Bot verwenden möchten, überprüfen Sie den Zick-Zack-Indikator als Einstiegspunkt.

Referenzen

1. StockCharts - eine Liste von Algorithmen mit Testdaten in den Tabellen.
2. Cryptowatch - gut abgestimmte Parameter der Indikatoren.
3. Github - mein Quellcode.

PS Wenn Sie Fehler im Text finden, teilen Sie mir dies bitte direkt mit.

Wie funktionieren technische Indikatoren an der Börse tatsächlich?